CAPÍTULO 6
GRANDEZAS E MEDIDAS
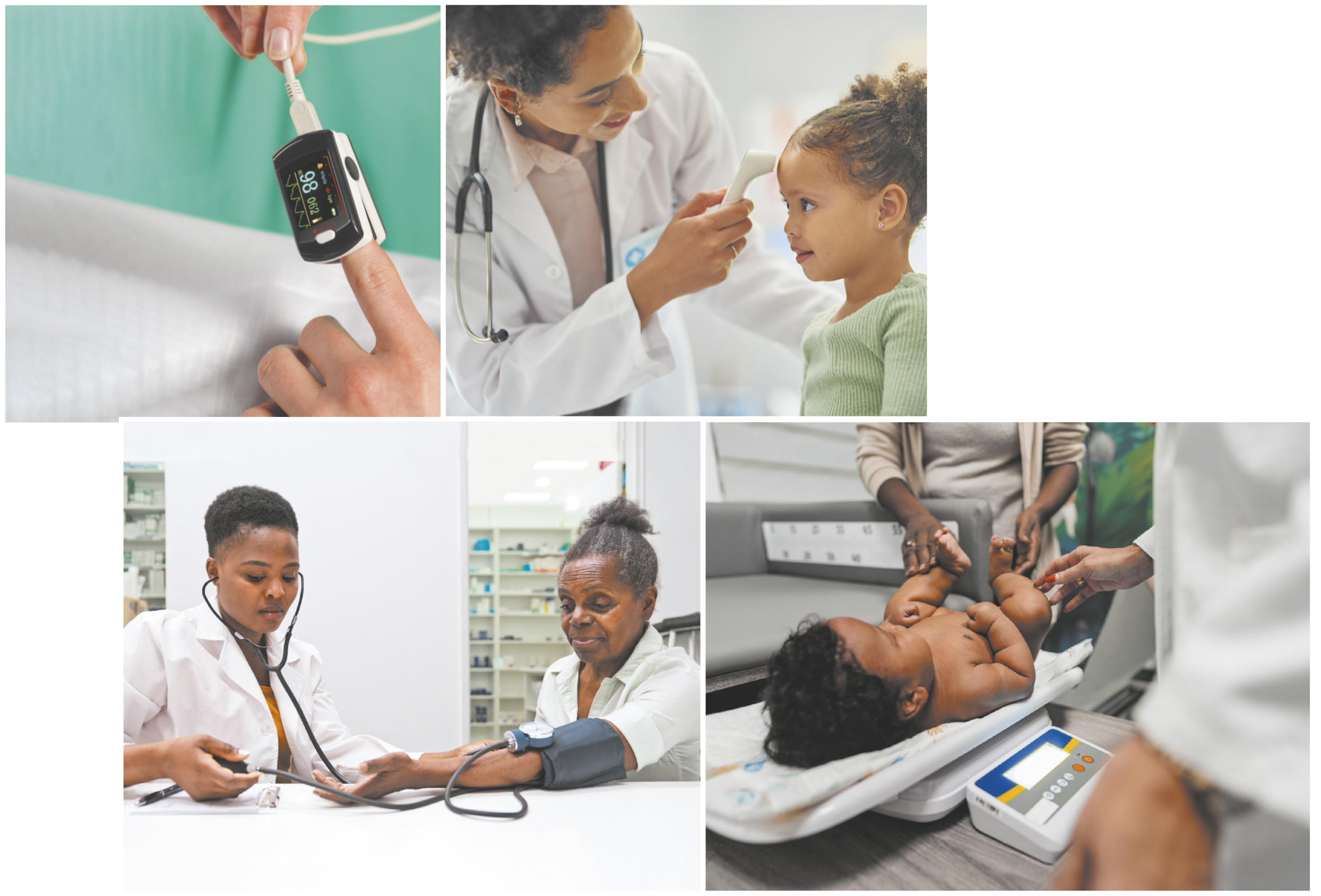
Quando uma pessoa passa pela triagem em uma consulta médica, o profissional da Enfermagem faz diversas medições, como a aferição da tempera-túra corporal, da pressão sanguínea, dos batimentos cardíacos e da oxigenação do sangue. No caso de bebês e crianças, também é comum fazer a medição da massa e da altura.
Essas informações são anotadas na ficha do paciente e repassadas ao médico quê fará o atendimento. Por esse motivo, é importante quê as medidas sêjam obtidas de maneira precisa e correta, para quê a saúde do paciente seja avaliada adequadamente.
Para quê um profissional de Enfermagem faça as medições necessárias, ele deve estar munido de instrumentos de medida adequados e calibrados, como o aparelho de medir a pressão e a balança.
É importante destacar quê a triagem médica tem funções diferentes em um consultório médico e em um pronto-socorro: no consultório, a triagem tem o papel de agilizar a consulta médica; já no pronto-socorro, a triagem tem a função de categorizar os casos, dando prioridade àqueles mais graves e urgentes.
Página duzentos e nove
![]() Agora, reúna-se a um colega, e façam o quê se pede em cada questão.
Agora, reúna-se a um colega, e façam o quê se pede em cada questão.
Ver as Orientações para o professor.
1. Vocês já repararam nas medições quê são feitas em triagens médicas? Discutam sobre a importânssia dêêsses procedimentos.
Resposta pessoal.
2. Nas imagens da abertura, o quê vocês acreditam quê está sêndo medido? Vocês sabem o nome do instrumento utilizado em cada situação?
2. Respostas pessoais. Espera-se quê os estudantes respondam: pressão sanguínea medida por um esfigmomanômetro; batimentos cardíacos e nível de oxigênio no sangue medidos por um oxímetro; tempera-túra corporal medida por um termômetro digital; e massa medida por uma balança.
3. Além dos instrumentos de medida quê aparécem nas imagens, quê outros instrumentos de medida você conhece?
3. Resposta pessoal. Os estudantes podem citar o relógio, o cronômetro e o calendário para medir o tempo, a régua, a trena e a fita métrica para medir comprimentos.
4. Que grandezas e quê unidades de medida dessas grandezas você conhece? Elabore uma lista e compare-a com a do colega.
Resposta pessoal.
Página duzentos e dez
Introdução
No cotidiano, lidamos com propriedades físicas dos objetos a todo momento. Por exemplo, para preparar um chá, primeiro elevamos a tempera-túra da á gua em uma chaleira e, depois, transferimos a á gua kemte para um recipiente adequado, como uma xícara ou uma caneca, sem exceder sua capacidade. Conforme a á gua é transferida de um recipiente para outro, sustentar a chaleira requer uma fôrça menor, uma vez quê diminui a massa de á gua quê ela contém.
Nesse cenário simples, citamos a interação com quatro grandezas: tempera-túra, capacidade, fôrça e massa.
Uma grandeza é uma propriedade mensurável. No dia a dia, medir uma grandeza é associar a ela um número, utilizando um instrumento apropriado.
Por exemplo, podemos utilizar o termômetro (instrumento) para aferir a tempera-túra (grandeza) de uma pessoa em grau célcius, em quê 1°C (um grau Celsius) é a unidade de medida préviamente adotada. Ou podemos usar uma trena (instrumento) para determinar o comprimento (grandeza) de uma sala em métro, em quê 1 m (um metro) é a unidade de medida préviamente adotada.

Comprimento, área e volume
Neste tópico, apresentaremos as noções básicas dos modelos matemáticos para a determinação de medidas das seguintes grandezas:
• Comprimento de um segmento de reta.
• Área de uma figura geométrica plana.
• Volume de um sólido geométrico.
Medir é estabelecer um sistema de comparação entre duas grandezas de mesma natureza, isto é, entre dois comprimentos, entre duas áreas ou entre dois volumes. Nesse sistema, uma das grandezas é adotada, préviamente, como unidade de medida, e o resultado da comparação é um número quê expressa quantas vezes a outra grandeza é maior, ou menor, do quê a unidade adotada.
Segmento unitário
Suponha quê queremos medir o comprimento do segmento .

Para isso, vamos adotar o segmento como unidade de medida e admitir quê a medida do seu comprimento será igual a 1, ou seja, uma unidade de comprimento (u.c.).

Página duzentos e onze
Nesse caso, o segmento é denominado segmento unitário.
Observe, na figura, quê o segmento cabe exatamente 5 vezes no comprimento de .

Portanto, a medida do comprimento de é 5 u.c. (cinco unidades de comprimento), ou seja, é cinco vezes maior do quê a unidade de medida adotada.
O segmento adotado como unidade de medida da grandeza comprimento é denominado segmento unitário, e, por definição, a medida do seu comprimento será igual a 1 u.c. (uma unidade de comprimento).
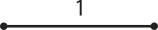
Quadrado unitário
Imagine, agora, quê queremos determinar a medida da área da região plana da figura geométrica F. Para isso, vamos adotar como unidade de medida o quadrado Q, cujo lado méde 1 u.c., e admitir quê a medida de sua área será igual a 1, ou seja, uma unidade de área (u.a.).
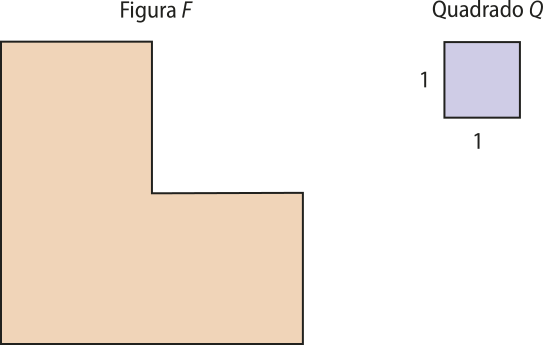
Nesse caso, o quadrado Q é denominado quadrado unitário.
Observe, na figura, quê o quadrado Q cabe exatamente 12 vezes na região plana da figura F.
Portanto, a medida da área da figura F é 12 u.a. (doze unidades de área), ou seja, a figura F é 12 vezes maior do quê a unidade de medida Q adotada.
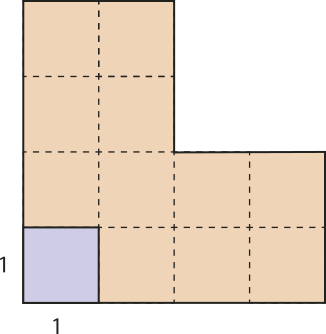
O quadrado cujo lado méde 1 u.c. (uma unidade de comprimento), adotado como unidade de medida da grandeza área, é denominado quadrado unitário, e, por definição, a medida da sua área será igual a 1 u.a. (uma unidade de área).

Página duzentos e doze
Cubo unitário
Vamos, agora, medir o volume do espaço ocupado pelo sólido geométrico S. Para isso, vamos adotar como unidade de medida o cubo C, cuja aresta méde 1 u.c., e admitir quê a medida do seu volume será igual a 1, ou seja, uma unidade de volume (u.v.).
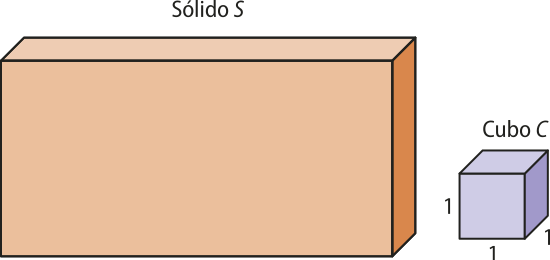
Nesse caso, o cubo C é denominado cubo unitário.
Observe, na figura, quê o cubo C cabe exatamente 18 vezes no espaço ocupado pelo sólido S.
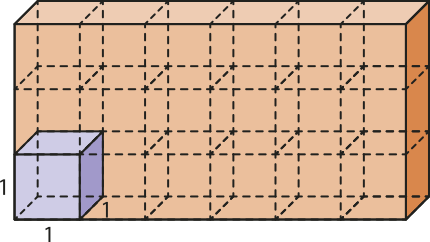
Portanto, o volume do sólido S é 18 u.v. (dezoito unidades de volume), ou seja, o sólido S é 18 vezes maior do quê a unidade de medida C adotada.
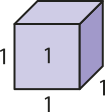
O cubo cuja aresta méde 1 u.c. (uma unidade de comprimento), adotado como unidade de medida da grandeza volume, é denominado cubo unitário, e, por definição, a medida do seu volume será igual a 1 u.v. (uma unidade de volume).
Saiba quê...
Nesta obra, os termos “comprimento”, “área” e “volume”, dependendo do contexto, serão usados tanto para indicar grandezas quanto suas respectivas medidas.
Em nosso cotidiano, quando temos de medir ou indicar o comprimento, a área e o volume de objetos reais, em geral, adotamos unidades de medidas padronizadas. Acompanhe alguns exemplos.
• O kilometro (km), para indicar o comprimento de uma rua. Nesse contexto, temos de imaginar o segmento unitário do modelo matemático com 1 km de comprimento.
• O métro quadrado (m2), para expressar a área de um terreno. Nesse exemplo, temos de imaginar os lados do quadrado unitário com 1 m de comprimento; portanto, por definição, sua área será igual a 1 m2.
• O decimetro cúbico (dm3), para quantificar o volume de á gua contido em um recipiente. Nesse caso, temos de imaginar as arestas do cubo unitário com 1 dm de comprimento; portanto, por definição, seu volume será igual a 1 dm3.
Porém, nem sempre existiram unidades padronizadas. Conheça um pouco a história das unidades de medida no próximo tópico.
Página duzentos e treze
O Sistema Internacional de Unidades (SI)
Há mais de uma maneira possível de associar um número a uma grandeza. Para medir o comprimento de uma quadra poliesportiva, uma pessoa poderia contar a quantidade de passos quê ela precisa dar para percorrê-la e associar essa quantidade ao comprimento da quadra. Nesse exemplo, essa pessoa poderia afirmar corretamente quê o comprimento dessa quadra é igual a 22 passos. No entanto, caso outra pessoa fizesse a medição da mesma quadra, também usando a quantidade de passos, ela poderia obtêr outro valor, por ter passos menóres quê a primeira pessoa, afirmando, também corretamente, quê o comprimento da quadra é igual a 31 passos. Nesses casos, dizemos quê o passo é a unidade de medida empregada para fazer a medição do comprimento da quadra. Porém, apesar de sêr uma unidade de medida válida, o passo não é uma unidade de medida usual, pois depende da pessoa quê realiza a medição.
Para contornar esse problema, ao longo dos séculos, cientistas propuseram unidades de medida padrão, quê independem das características físicas de quem realiza a medição.
Acompanhe a linha do tempo a seguir.
Final do século XVIII
No caso da grandeza comprimento, a unidade de medida métro foi definida como uma fração específica da distância entre o Equador e o Polo Norte ao longo de um meridiano.
1875
Foi fundada a Conferência Geral de Pesos e mêdídas (CGPM), uma organização internacional quê atua como autoridade em todas as kestões relacionadas às unidades de medida. Na ocasião, delegações de 17 países se reuniram para estabelecer um sistema de medidas internacionalmente aceito.
1954
Desde sua fundação, a CGPM tem se reunido periodicamente, e, em sua 10ª reunião, foram adotadas como base as unidades de sete grandezas.
1799
A unidade métro foi redefinida como a distância entre duas marcas gravadas em uma barra de platina, as quais foram feitas de modo a corresponder à definição anterior. Essa barra de platina, conhecida como métro padrão, foi armazenada em Paris, na França, em uma sala com tempera-túra e umidade estáveis para minimizar variações no tamãnho dela.
1889
Ocorre a primeira reunião da CGPM em Paris. Durante essa conferência, cópias do métro padrão original foram adotadas, e outras medidas foram tomadas para consolidar, internacionalmente, o sistema métrico.
1960
Em sua 11ª reunião, a CGPM adotou o nome Sistema Internacional de Unidades (SI) para o sistema propôsto seis anos antes.
Página duzentos e quatorze
As sete grandezas escolhidas pela CGPM não dependem umas das outras e são denominadas grandezas de base; suas unidades são conhecidas como unidades de base e podem sêr observadas no qüadro a seguir.
Grandeza de base |
Unidade de base (sín-bolo) |
|---|---|
Comprimento |
métro (m) |
Massa |
kilograma (kg) |
Tempo |
segundo (s) |
Temperatura termodinâmica |
kelvin (K) |
Quantidade de matéria |
mol (mol) |
Intensidade luminosa |
candela (cd) |
Corrente elétrica |
ampere (A) |
Saiba quê...
Atualmente, no SI, o métro é definido em função da velocidade da luz no vácuo (c); o kilograma, em função da constante de Planck (h); o segundo, em função de determinado período de radiação ligado ao césio-133; o kelvin, em função da constante de Boltzmann (k); o mol, em função da constante de Avogadro (NA); a candela, em função da eficácia luminosa de uma fonte de luz em uma freqüência específica; e o ampere, em função da carga elementar do elétron (e).
Apesar de o SI contemplar todas as unidades de medida necessárias para medir as grandezas físicas, no dia a dia, costumamos utilizar algumas unidades de medida quê não pertencem a esse sistema. Por exemplo:
• A tonelada (unidade de medida de massa, quê corresponde a 1.000 kg).
• O litro (unidade de medida de volume, quê corresponde a 0,001 m3).
• O minuto (unidade de medida de tempo, quê corresponde a 60 s).
• A hora (unidade de medida de tempo, quê corresponde a 3.600 s).
• O grau célcius (unidade de medida de temperatura).

Pense e responda
No SI, a unidade de medida referente à grandeza ângulo plano é o radiano (rad). Que outra(s) unidade(s) de medida associada(s) a essa grandeza você conhece?
Resposta pessoal. Exemplo de resposta: o grau (°).
Embora a maioria dos países tenha adotado o SI como sistema oficial de medidas, alguns países não o adotaram por completo e continuam a utilizar sistemas de medidas diferentes em certos contextos. Os Estados Unidos e o Reino Unido são dois exemplos onde o sistema imperial de medidas é usado cotidianamente. Esse sistema inclui a polegada (in), o pé (ft), a jarda (yd) e a milha (mi) como unidades de medida de comprimento, a libra (lb) e a onça (oz) como unidades de medida de massa e o grau farenrráiti (°F) como unidade de medida de tempera-túra.
Página duzentos e quinze
Escrita da medida de uma grandeza
Por convenção do SI, a notação utilizada para escrever a medida de uma grandeza é composta de um número, um espaço e uma unidade, por exemplo:
• 2 m (dois metros)
• 0,1 s (um décimo de segundo)
Interpretamos essas notações como um produto entre o número e a unidade, ou seja:
• 2 m = 2 ⋅ m
• 0,1 s = 0,1 ⋅ s
O primeiro exemplo mostra quê o comprimento mensurado é duas vezes maior do quê a unidade de medida adotada, no caso, o métro, e o segundo exemplo mostra quê o tempo mensurado é dez vezes menor do quê a unidade de medida adotada, no caso, o segundo.
Ao escrever a medida de uma grandeza como um produto, tanto o número quanto a unidade podem sêr manipulados algebricamente, o quê possibilita a conversão entre unidades e a utilização de prefixos por meio de manipulações algébricas.
Prefixos
O métro, quê é uma unidade de base do SI, é bastante útil para medir vários comprimentos no nosso dia a dia. No entanto, há situações em quê o métro não é a unidade mais conveniente. Por exemplo:
• A distância, em linha reta, entre os municípios mineiros Ouro Preto e Ouro Branco é 25.000 m.
• O comprimento da bactéria Escherichia cóli póde chegar a apenas 0,000002 m.
Embora essas medidas estejam corretas, elas não são convenientes. Para casos como esses, utilizamos múltiplos e submúltiplos do métro.
Quando acrescentamos um prefixo à unidade de medida, compomos uma nova unidade, quê é um múltiplo ou um submúltiplo da unidade de base. A seguir, apresentamos alguns dos prefixos adotados no SI, seus símbolos e seus fatores de multiplicação.
Prefixo |
Símbolo |
Fator |
|---|---|---|
tera |
T |
1012 |
giga |
G |
109 |
mega |
M |
106 |
kilo |
k |
103 |
hecto |
h |
102 |
deca |
da |
101 |
deci |
d |
10−1 |
centi |
c |
10−2 |
mili |
m |
10−3 |
micro |
µ |
10−6 |
nano |
n |
10−9 |
pico |
p |
10−12 |
Pense e responda
Que comprimentos você mediria utilizando a unidade de medida métro?
Resposta pessoal. Espera-se quê os estudantes citem altura de pessoas ou de edifícios, comprimento de veículos, entre outros.
Página duzentos e dezesseis
Assim, adicionando o prefixo kilo (k) à unidade métro (m), compomos a unidade múltipla do métro chamada kilometro (km), e, adicionando o prefixo micro (μ) à unidade métro (m), compomos a unidade submúltipla do métro chamada micrometro (μm). Conforme o qüadro, temos:
• 103 m = 1 km
• 10−6 m = 1 μm
Desse modo, as medidas 25.000 m e 0,000002 m são equivalentes a:
25.000m = 25 ⋅ 1.000m = 25 ⋅ = 25km
0, 000002m = 2 ⋅ = 2 μm
Assim, podemos expressar a distância entre os municípios Ouro Preto e Ouro Branco e o comprimento da bactéria Escherichia cóli como 25km e 2μm, respectivamente.
De maneira geral, a unidade métro póde sêr convertida para kilometro e para micrometro do seguinte modo:
103m = 1km ⇒ 1m = km
10−6m = 1μm ⇒ 1m = 106μm

Os prefixos apresentados no qüadro anterior podem sêr utilizados com outras unidades de medida além do métro, inclusive com várias unidades quê não fazem parte do SI, como os múltiplos e submúltiplos do litro (kilolitro, hectolitro, decalitro, decilitro, centilitro e mililitro). No entanto, esses prefixos não são utilizados com as unidades de medida de tempo quê não pertencem ao SI, como o minuto e a hora.
Já o kilograma, unidade de base para a grandeza massa, é um caso especial. Ele contém o prefixo kilo por motivos históricos. Por convenção, os múltiplos e submúltiplos dessa unidade de medida são obtidos pela substituição do prefixo kilo por outro, mantendo o radical da palavra (grama). Por exemplo, as unidades de medida micrograma e nanograma, quê correspondem a 10−6 g e 10−9 g, respectivamente.

Página duzentos e dezessete
Unidades de área
O métro quadrado (m2) é a unidade de medida padrão do SI para a grandeza área, e o quadrado unitário, cujo lado méde 1 m de comprimento, terá, por definição, 1m2 de área.
As unidades múltiplas e submúltiplas do métro quadrado (m2) utilizam fatores diferentes dos apresentados no qüadro de prefixos. Observe a comparação entre alguns fatores do métro e do métro quadrado.
Unidade de comprimento |
km |
hm |
dam |
dm |
cm |
mm |
|---|---|---|---|---|---|---|
Fator |
103 |
102 |
101 |
10−1 |
10−2 |
10−3 |
Unidade de área |
km2 |
hm2 |
dam2 |
dm2 |
cm2 |
mm2 |
Fator |
106 |
104 |
102 |
10−2 |
10−4 |
10−6 |
De acôr-do com o qüadro de comparação, temos:
• 1 dm = 10−1 m ⇒ 1 dm = m
• 1 dm2 = 10−2 m2 ⇒ 1 dm2 = m2
Observe quê, enquanto um decimetro equivale a um décimo do métro, um decimetro quadrado equivale a um centésimo do métro quadrado.
Para entender essa diferença, acompanhe o procedimento a seguir, quê compara a medida da área de um quadrado, em decimetro quadrado (dm²), à medida dessa mesma área, em métro quadrado (m²).
A área de um quadrado, cujo lado méde 10 dm, é 100 dm², pois 102 = 100. Entretanto, dez decimetros equivalem a um métro (10 dm = 1 m), ou seja, o mesmo quadrado tem 1 m de lado e, consequentemente, 1 m² de área.
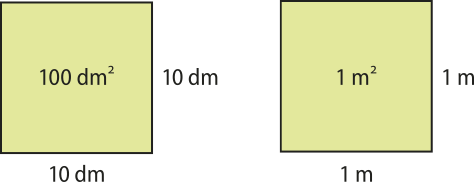
Desse modo, temos:
100 dm2 = 1 m2 ⇒ ⇒ dm2 = 10−2 m2
Portanto, um decimetro quadrado corresponde a um centésimo do métro quadrado. pôdêmos fazer esse procedimento, com adequações necessárias, para obtêr os demais fatores das unidades múltiplas e submúltiplas do métro quadrado.
Página duzentos e dezoito
Unidades de volume
O métro cúbico (m³) é a unidade de medida padrão do SI para a grandeza volume, e o cubo unitário, cuja aresta méde 1 m de comprimento, terá, por definição, 1 m³ de volume.
As unidades múltiplas e submúltiplas do métro cúbico (m3) também utilizam fatores diferentes dos apresentados no qüadro de prefixos. Observe.
Unidade |
km3 |
hm3 |
dam3 |
dm3 |
cm3 |
mm3 |
|---|---|---|---|---|---|---|
Fator |
109 |
106 |
103 |
10−3 |
10−6 |
10−9 |
De acôr-do com o qüadro e com o quê estudamos anteriormente, temos quê:
• 1 dm = 10−1 m ⇒ 1 dm = m
• 1 dm3 = 10−3 m3 ⇒ 1 dm3 = m3
Nesse caso, enquanto um decimetro equivale a um décimo do métro, um decimetro cúbico equivale a um milésimo do métro cúbico.
Para entender essa diferença, acompanhe um modo de obtêr o fator do decimetro cúbico.
O volume de um cubo, cuja aresta méde 10 dm, é 1.000 dm³, pois 103 = 1.000. Entretanto, dez decimetros equivalem a um métro (10 dm = 1 m), ou seja, o mesmo cubo tem 1 m de aresta e, consequentemente, 1 m³ de volume.
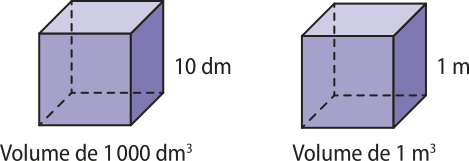
Desse modo, temos:
1.000 dm3 = 1 m3 ⇒ = ⇒ 1 dm3 = 10−3m3
Assim, um decimetro cúbico corresponde a um milésimo do métro cúbico. De maneira análoga e com adequações necessárias, podemos obtêr os demais fatores das unidades múltiplas e submúltiplas do métro cúbico.
Saiba quê...
O litro (L) é uma unidade de volume muito utilizada, a qual não pertence ao SI. O fator de conversão dessa unidade de medida para o métro cúbico é:
1L = 10−3 m3
Manipulando essa relação, temos outras equivalências. Por exemplo:
• Um litro equivale a um decimetro cúbico (1 L = 1 dm³).
• Mil litros correspondem a um métro cúbico (1.000 L = 1 m³).
• Um mililitro equivale a um centimetro cúbico (1 mL = 1 cm³).
Página duzentos e dezenove
Instrumentos de medida
Em nosso cotidiano, para medidas de comprimento, estamos acostumados a utilizar alguns instrumentos, como a régua graduada, a fita métrica e a trena. Esses três instrumentos de medida costumam sêr graduados em centimetros e milimetros e têm precisão de 1 mm.
Para profissionais quê precisam de uma maior precisão em suas aferições, o paquímetro é uma opção. Esse instrumento costuma ter precisão de 0,1 mm, 0,05 mm e 0,02 mm.
- precisão
- : a precisão de um instrumento de medida é a menor divisão na escala quê ele adota.
Para assistir
• COMO usar um paquímetro: a régua turbinada. [S. l.: s. n.], 2016. 1 vídeo (6 min). Publicado pelo canal Manual do Mundo. Disponível em: https://livro.pw/wsebb. Acesso em: 26 ago. 2024.
Assista ao vídeo para aprender, de modo simples, a usar um paquímetro.

O micrômetro tem maior precisão do quê o paquímetro: entre 0,01 mm e 0,001 mm. Em geral, ele é utilizado para medir objetos muito pequenos, como o diâmetro de um fio de cabelo.
Já para medidas de massa, utilizamos balanças. No entanto, para cada situação, há um tipo de balança mais adequado.
Em depósitos e indústrias, balanças de carga são amplamente utilizadas. Elas varíam de formato e de capacidade dependendo da aplicação específica em quê são utilizadas. A precisão das balanças de carga costuma sêr de 0,1% da capacidade delas, o quê significa, por exemplo, quê uma balança de carga com capacidade de 10 t tem precisão de 10 kg.
Para uso doméstico, existe a balança de massa corporal, quê é utilizada para aferir a massa corpórea, com precisão de 0,1 kg, e a balança culinária, quê é utilizada para medir a massa de alimentos, com precisão de 1g.
Em situações quê exigem a medição precisa de massa, como em joalherias, laboratórios e indústria farmacêutica, são utilizadas balanças cuja precisão é em torno de 0,1 mg, podendo chegar a 0,01 mg em modelos avançados.

Página duzentos e vinte
Além dêêsses, existem outros instrumentos de medida. Acompanhe alguns exemplos.
• O cronômetro é um instrumento de medida de tempo e tem precisão de 1 centésimo de segundo.
• O copo medidor de líquidos méde o volume de líquidos. Ele é vendido em diferentes modelos, cada um com uma precisão própria, mas costuma variar entre 50 mL e 100 mL.
• O copo dosador de medicamentos, usado para medir o volume de medicamentos líquidos, tem precisão de poucos mililitros, sêndo comum o copo dosador com precisão de 2,5 mL.
• O termômetro utilizado para medir tempera-túra corporal tem precisão de 0,1 °C, enquanto os termômetros quê médem a tempera-túra ambiente e os quê são utilizados na culinária têm precisão de 1°C.
Algarismos significativos e algarismos duvidosos
Quando utilizamos um instrumento para medir a grandeza de um objeto real, o resultado obtído é acompanhado de um êrro, de uma imprecisão ocasionada pelas características do instrumento utilizado. Observe.
Vamos considerar duas medições para um lápis: a primeira delas feita com uma régua graduada em centimetro, e a segunda, com uma régua graduada em milimetro.
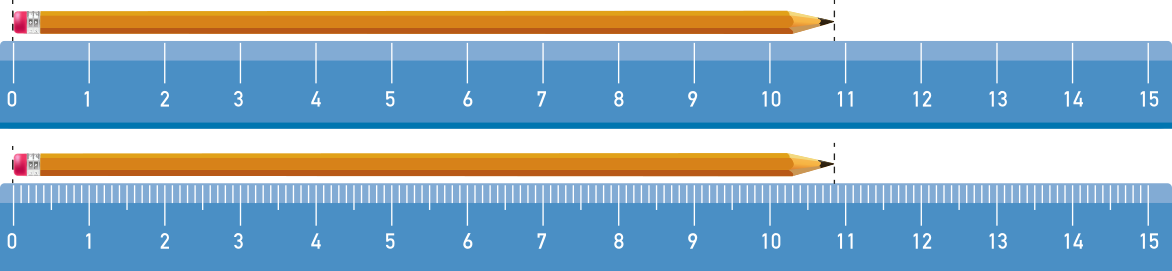
Na primeira medição, observamos quê a ponta do lápis está entre os números 10 e 11, podendo concluir quê o lápis tem mais de 10 cm e menos de 11 cm. Como a ponta está mais próxima do número 11 quê do número 10, podemos estimar quê a medida do lápis seja 10,8 cm. Note quê a estimativa 10,9 cm, para a medida dêêsse lápis por meio dessa régua, também seria válida.
Na segunda medição, observamos quê a ponta do lápis está entre os números 10,8 e 10,9, podendo concluir quê o lápis tem mais de 10,8 cm e menos de 10,9 cm. Como a ponta está entre esses números, podemos estimar quê a medida do lápis seja 10,85 cm.
Para a medida 10,8 cm encontrada na primeira medição, dizemos quê os algarismos 1 e 0 são certos e quê o algarismo 8 é duvidoso, uma vez quê ele foi estimado. Já para a medida 10,85 cm encontrada na segunda medição, dizemos quê os algarismos 1, 0 e 8 são certos e quê o algarismo 5 é duvidoso.
Chamamos de algarismos certos aqueles quê são obtidos diretamente na medição e de algarismos duvidosos aqueles quê são estimados por quêm realiza a medição. Dizemos que todos os algarismos certos e o primeiro duvidoso são os algarismos significativos de uma medida.
Assim, podemos dizêr quê a medida 10,8 cm determinada com a primeira régua tem 3 algarismos significativos, enquanto a medida 10,85 cm determinada com a segunda régua tem 4 algarismos significativos.
Página duzentos e vinte e um
ATIVIDADES RESOLVIDAS
1. (UTFPR) Convertendo 843 dm (decimetros) e 35 km (kilometros) para metros, obtemos, respectivamente:
a) 8,43 e 3.500 metros.
b) 84,3 e 35.000 metros.
c) 0,843 e 350 metros.
d) 8.430 e 3,5 metros.
e) 84.300 e 35 metros.
Resolução
Sabemos quê 1 dm = 10−1 m e 1 km = 103 m,
logo:
843 dm = 843 ⋅ 10−1 m = 84,3 m
35 km = 35 ⋅ 103 m = 35.000 m
Portanto, as conversões corretas estão na alternativa b.
2. (UTFPR) Um salão póde sêr revestido totalmente com 540 ladrilhos de 3.600 cm2, cada um. Assinale qual a área do salão.
a) 19,40 dm2.
b) 1,94 km2.
c) 0,194 hm2.
d) 194.000 mm2
e) 194,40 m2.
Resolução
A área do salão é:
540 ⋅ 3.600 cm2 = 1.944.000 cm2
Como 1 cm2 = 10−4 m2, então:
1.944.000 cm2 = 1.944.000 ⋅ 10−4 m2 = 194,40 m2
A área do salão está expressa corretamente na alternativa e.
3. (Enem/MEC) Os tempos gastos por três alunos para resolver um mesmo exercício de matemática foram: 3,25 minutos; 3,4 minutos e 191 segundos.
O tempo gasto a mais, em segundo, pelo aluno quê concluiu por último a resolução do exercício, em relação ao primeiro quê o finalizou, foi igual a
a) 13.
b) 14.
c) 15.
d) 21.
e) 29.
Resolução
Para converter minutos (min) em segundos (s), utilizamos a seguinte equivalência:
1 min = 60 s
Assim, os tempos, em segundo, quê os três alunos gastaram para resolver o exercício foram:
Aluno 1: 3,25 min = 3,25 ⋅ 60 s = 195 s
Aluno 2: 3,4 min = 3,4 ⋅ 60 s = 204 s
Aluno 3: 191 s
Portanto, o aluno quê concluiu o exercício por último gastou 204 s, e o quê concluiu primeiro gastou 191 s. Assim, a diferença de tempo entre eles é dada por:
204 s − 191 s = 13 s
Portanto, a resposta correta é a alternativa a.
4. (FGV-SP) Estima-se quê, em determinado país, o consumo médio por minuto de farinha de trigo seja 4,8 toneladas. Nessas condições, o consumo médio por semana de farinha de trigo, em kilogramas, será aproximadamente:
a) 4,2 ⋅ 105
b) 4,8 ⋅ 107
c) 5,0 ⋅ 107
d) 4,6 ⋅ 106
e) 4,4 ⋅ 106
Resolução
Pelo enunciado, o consumo médio de farinha de trigo é .
Sabemos quê 1 semana tem 7 dias, quê cada dia tem 24 horas e quê cada hora tem 60 minutos. Assim:
7 ⋅ 24 ⋅ 60 min = 1 semana ⇒
⇒ 1 min = semana
Como o exercício pede um valor aproximado em notação científica, vamos arredondar 10.080 para 104. Com isso, temos quê:
1 min = semana ⇒ 1 min = 10−4 semana
Além díssu, sabemos quê uma tonelada = 10³ kg.
Logo, o consumo médio, em kilograma por semana, será de aproximadamente:
= 4,8 ⋅ 107
Portanto, a resposta correta é a alternativa b.
Página duzentos e vinte e dois
ATIVIDADES
1. (hú éfe pê érre) Na representação de grandezas físicas, são utilizados diferentes sistemas de unidades, sêndo quê o SI (Sistema Internacional de Unidades) é o sistema padrão utilizado pela comunidade científica. Uma unidade básica do SI, a unidade de medida do comprimento, é:
a) a milha.
b) o métro.
c) o pé.
d) a polegada.
e) a jarda.
alternativa b
2. (IFPE) Na disciplina Instalações de Refrigeração, do 6º período do curso de Refrigeração e Climatização do IFPE campus Recife, um estudante precisou fazer um orçamento para a compra de 8 metros de tubo de cobre. Ao pesquisar em algumas lojas, percebeu quê o preêço era informado de acôr-do com o comprimento do tubo, em centimetros ou em decimetros. Esse estudante concluiu quê precisava fazer um orçamento de
a) 8.000 centimetros de tubo.
b) 80 centimetros de tubo.
c) 800 centimetros de tubo.
d) 800 decimetros de tubo.
e) 8.000 decimetros de tubo.
alternativa c
3. (Enem/MEC) A Chlamydia, a menor bactéria do mundo, méde cerca de 0,2 micrometro (1 micrometro equivale à milionésima parte de um metro). Para ter uma noção de como é pequena a Chlamydia, uma pessoa rêzouvêo descrever o tamãnho da bactéria na unidade milimetro. A medida da Chlamydia, em milimetro, é
a) 2 × 10−1
b) 2 × 10−2
c) 2 × 10−4
d) 2 × 10−5
e) 2 × 10−7
alternativa c
4. Leia um trecho da notícia a seguir e faça o quê se pede.
A Polícia Rodoviária Federal (PRF) apreendeu arma de fogo, ouro de garimpo ilegal, minério, e combustível de aviação contrabandeados durante abordagens neste fim de semana nas rodovias BR-174 e BR-401, em Roraima. […]
De acôr-do com a PRF, foram 22 munições, 60 gramas de ouro, 1,5 kg de minerais e 1,5 litro de combustível.
PRF apreende arma de fogo, ouro, minérios e combustível de aviação contrabandeados em rodovias de Roraima. G1, Boa vista, 15 abr. 2024. Disponível em: https://livro.pw/yjqbp. Acesso em: 26 ago. 2024.
a) Liste as unidades de medida citadas no texto e as grandezas a quê correspondem.
Grama (g) – unidade de medida de massa; kilograma (kg) – unidade de medida de massa; litro (L) – unidade de medida de volume.
b) Expresse a quantidade de combustível apreendida utilizando uma unidade do SI.
Exemplos de resposta: 0,0015 m3; 1,5 dm3
c) Expresse as outras medidas utilizando uma unidade de base do SI.
Quantidade de ouro: 0,06 kg. A quantidade de minerais (1,5 kg) já está expressa usando uma unidade de base do SI (kg).
5. (Cefet-RJ) Um relógio digital mostra as horas de 00:00 até 23:59. Em alguns momentos, o relógio mostra horas seguidinhas, isto é, apresenta sequência de quatro números consecutivos. Por exemplo, 12:34 é uma hora seguidinha.
De 12:34 até a próxima hora seguidinha, quantos minutos terão passado?
a) 671
b) 661
c) 651
d) 641
alternativa a
6. (Enem/MEC) Com o intuito de fazer bôm-bôns para vender, uma doceira comprou uma barra de 2 kg de chocolate e 1 L de creme de leite. De acôr-do com a receita, cada bombom deverá ter exatamente 34 g de chocolate e 12mL de creme de leite.
Respeitando os critérios estabelecidos, quantos bôm-bôns a doceira poderá fazer utilizando o mássimo quê puder os ingredientes comprados?
a) 5
b) 8
c) 58
d) 71
e) 83
alternativa c
7. (í éfi cê ê) A carga de um caminhão é de duas toneladas. Se já foram carregados 920 kg, a quantidade de kilogramas quê ainda falta é
a) 1.060.
b) 1.080.
c) 1.100.
d) 1.120.
e) 1.140.
alternativa b
Página duzentos e vinte e três
8. Faça a conversão das unidades de medida.
a) Uma área de 15.000 cm2 equivale a quantos metros quadrados?
1,5 m2
b) Um volume de 5 m3 corresponde a quantos litros?
5.000 L
c) Uma área de 0,003 km2 equivale a quantos centimetros quadrados? escrêeva a resposta em notação científica.
3 ⋅ 107 cm2
d) Um volume de 2.500 mL corresponde a quantos metros cúbicos? escrêeva a resposta em notação científica.
2,5 ⋅ 10−3 m3
9. (Encceja/MEC) Uma criança está aprendendo a utilizar a régua e rêzouvêo medir o comprimento de uma caneta, posicionando uma régua, graduada em centimetro, como ilustra a figura.
A medida do comprimento dessa caneta, em centimetro, é

a) 11,0.
b) 11,4.
c) 11,6.
d) 12,0.
alternativa c
10. No exercício anterior, quantos algarismos significativos tem a medida da caneta? Quantos dêêsses algarismos são certos e quantos são duvidosos?
O comprimento 11,6 cm da caneta tem três algarismos significativos, dois deles são certos, e o outro é duvidoso.
11. (Encceja/MEC) Para efetuar a medida de uma grandeza, precisamos estabelecer uma unidade de medida como referência para, a partir daí, definir o comprimento, a área, a massa ou o quê se quer medir.
Observe a tirinha.

SILVA, W. R. Disponível em: https://livro.pw/juskd. Acesso em: 12 set. 2019.
O personagem Caco, a fim de impressionar seu amigo, determinou a sua altura em um submúltiplo do métro, quê é a unidade padrão no Sistema Internacional de Unidades para medir a grandeza comprimento. Pode-se considerar quê ele não está sêndo exagerado, pois a altura média de um animal adulto da sua espécie é de 1,50 m. Com base nessas informações, quantos centimetros devem sêr somados à medida da altura de Caco para alcançar a média de altura de um animal adulto de sua espécie?
a) 70
b) 65
c) 7
d) 0,7
alternativa a
12. (hú- hê- érre jota)

novaescola.org.br
Onça e libra são unidades de massa do sistema inglês. Sabe-se quê 16 onças equivalem a 1 libra e quê 0,4 onças é igual a x libras. O valor de x é igual a:
a) 0,0125
b) 0,005
c) 0,025
d) 0,05
alternativa c
Página duzentos e vinte e quatro
Unidades de grandezas derivadas
Chamamos de unidades de grandezas derivadas aquelas quê podem sêr obtidas por meio de uma razão ou de um produto de unidades de bases, ou de seus múltiplos ou submúltiplos.
Vamos analisar alguns casos.
Velocidade
As unidades de medida mais utilizadas para a grandeza velocidade são o métro por segundo e o kilometro por hora ().
Para converter unidades quê são indicadas por uma razão, dependendo do contexto, é necessário mudar as unidades das duas grandezas. O exemplo a seguir ilustra como converter km/h para m/s.
Considere a seguinte situação.
Um veículo se desloca a uma velocidade média de 72 km/h. Como podemos determinar essa velocidade em métro por segundo (m/s), quê é a unidade padrão para velocidade no SI?
Primeiro, temos de estabelecer as equivalências entre as unidades de comprimento e entre as unidades de tempo.
Sabemos quê 1 km = 103 m.
Em relação à unidade de tempo, temos quê 1 h = 60 min e 1 min = 60 s.
Portanto:
1 h = 60 min = 60 ⋅ 60 s = 3.600 s
Substituindo as unidades km e h por suas respectivas equivalências, obtemos:
72 km/h = = 20 m/s
Logo, a velocidade média do veículo, em métro por segundo, é 20 m/s.
Saiba quê...
É comum as unidades de medida de velocidade serem escritas no formato m/s e km/h. Independentemente da escrita, elas expressam uma razão entre as unidades das grandezas comprimento e tempo.
Pense e responda
Se um objeto se móve a uma velocidade média de 25 m/s, qual é a velocidade dêêsse objeto em kilometro por hora?
90 km/h

Página duzentos e vinte e cinco
Densidade
Dizemos quê a densidade é a grandeza quê relaciona a massa de um objeto ao espaço quê ele ocupa. Ela é determinada pela seguinte razão:
densidade =
As unidades derivadas quê são associadas à densidade são a razão entre unidades de medida de massa e unidades de medida de volume, sêndo as mais comuns o kilograma por métro cúbico ( ) e o grama por centimetro cúbico ().
Densidade superficial
Quando se tratam de materiais, como tecídos e papéis, é comum relacionar a massa deles à área por meio da grandeza densidade superficial, quê póde sêr calculada pela seguinte razão:
densidade superficial =
Para densidade superficial, as unidades derivadas mais comuns são o kilograma por métro quadrado (kg/m2) e o grama por métro quadrado (g/m2).

Saiba quê...
Nas indústrias têxtil e de papel, a densidade superficial costuma sêr chamada de gramatura.
Densidade demográfica
A concentração de pessoas em determinada região geográfica é denominada densidade demográfica. A densidade demográfica é dada pela razão entre o número de habitantes de uma região e a área dessa região.
densidade demográfica =
A densidade demográfica é, geralmente, expressa em habitantes por kilometro quadrado (habitantes/km2).
Essa medida é importante para entender como a população está distribuída em diferentes regiões, sêndo útil para o planejamento urbano, para a distribuição de recursos, para o cálculo de impactos ambientais e para outros aspectos socioeconômicos. Alguns fatores quê influenciam na densidade demográfica são o relevo, o clima, a disponibilidade de recursos e o desenvolvimento econômico.
Página duzentos e vinte e seis
FÓRUM
Populoso ou povoado?
O Brasil é um país populoso. De acôr-do com o Censo 2022, feito pelo Instituto Brasileiro de Geografia e Estatística (hí bê gê hé), a população do país é de mais de 200 milhões de habitantes; mas seria o Brasil um país povoado? Para responder a essa pergunta, devemos entender a diferença entre esses dois conceitos da Geografia.
Populoso se refere à quantidade de habitantes de uma região, sem considerar sua extensão territorial nem a distribuição da população.
Já povoado se refere à densidade demográfica. Uma região com uma densidade demográfica alta é considerada densamente povoada, mesmo quê sua população não seja tão grande. Para isso, basta quê sua área seja pequena, por exemplo.
Compreendendo isso, concluímos quê o Brasil é um país populoso, pois sua população é muito grande, mas nem todo o país é densamente povoado, já quê sua extensão territorial é muito grande, e a população está mal distribuída dentro do território.
Observe o mapa a seguir.
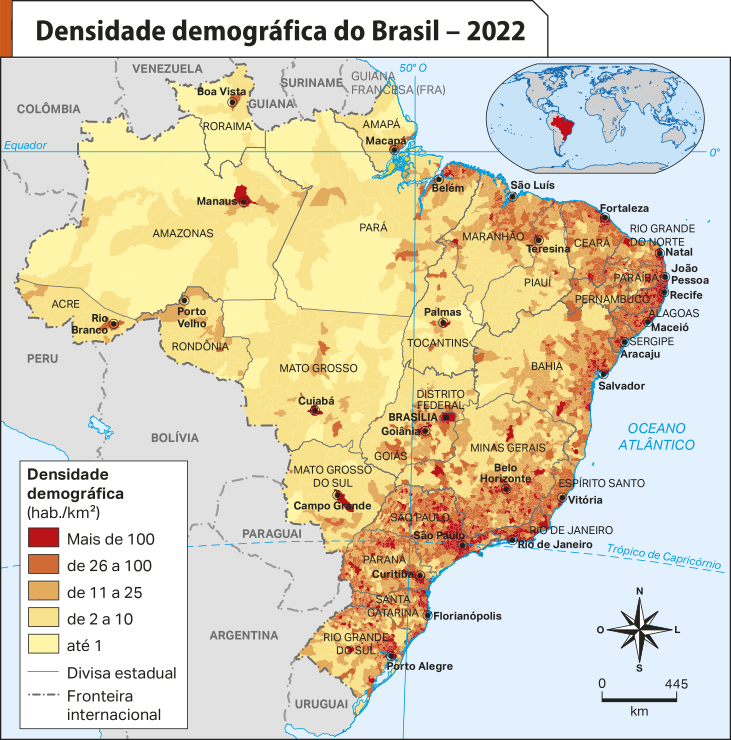
Fonte: INSTITUTO BRASILEIRO DE GEOGRAFIA E ESTATÍSTICA. Atlas geográfico escolar. 9. ed. Rio de Janeiro: hí bê gê hé, 2023. p. 118.
A distribuição desigual da população dentro de um território póde trazer grandes problemas sociais e econômicos, tanto para as regiões densamente povoadas como para as pouco povoadas.
![]() Após a leitura do texto e a análise do mapa, faça o quê se pede.
Após a leitura do texto e a análise do mapa, faça o quê se pede.
• Com seus côlégas, façam um fórum de debate sobre os problemas causados pela má distribuição da população no território brasileiro e sobre as possíveis ações quê poderiam reduzir essa distribuição desigual.
Ver as Orientações para o professor.
Página duzentos e vinte e sete
Potência e consumo de energia elétrica
A unidade de medida de energia é o kilowatt-hora (kWh), ôbitída como produto entre as unidades de potência (kW) e de tempo (h), ou seja, kWh = kW ⋅ h. Essa unidade de medida representa a quantidade de energia consumida por um dispositivo ou por um sistema durante um período de tempo; ela é usada para cobranças de energia elétrica em domicílios e empresas.
Um kilowatt-hora é equivalente a 1.000 watts de potência utilizada continuamente por uma hora.
Para entender a maneira como calcular o consumo de energia, vamos tomar como exemplo um noutibúk cuja potência é 230 W, quê fica ligado durante 8 h por dia, ao longo de 25 dias em um mês. Durante esse período de uso, a energia E gasta por esse equipamento é:
= 230 ⋅ 10−3 kW ⋅ 200 h = 46 kWh
Em uma região em quê o preêço do kWh é R$ 0,65, o custo gerado em um mês, considerando-se apenas esse aparelho, é 29,90 reais, pois 46 ⋅ 0,65 = 29,90.

■ O sêlo Procel, presente em elétro domésticos vendidos no Brasil, indica o nível de eficiência energética do produto. Quando um aparelho tem alta eficiência energética, significa quê ele utiliza a energia de maneira mais eficaz, reduzindo o consumo de energia elétrica.
ATIVIDADES RESOLVIDAS
5. (Eear-SP) A densidade é uma grandeza física quê varia com a mudança da tempera-túra e da pressão, sêndo quê nos sólidos e nos líquidos essa variação é muito pequena, enquanto quê nos gases é maior. No Sistema Internacional de Unidades (SI), a densidade é dada em kg/m3, porém, é muito comum o uso do g/cm3.
Dentre as alternativas a seguir, assinale aquela na qual está corretamente descrito o valor de 1 g/cm3 expresso em unidades do SI (kg/m3).
a) 0,001
b) 0,01
c) 100
d) 1.000
Resolução
A unidade da densidade é indicada por uma razão entre as unidades de massa e de volume. Então, para converter 1g/cm3 em kg/m3, precisamos mudar as duas unidades. Em relação à unidade de massa, sabemos quê 1g = 10−3 kg. Em relação à unidade de volume, temos 1 cm3 = 10−6 m3. Desse modo:
1 g/cm3 = 1
= 103 = 1.000 kg/m3
Portanto, a alternativa d é a correta.
6. (UFRGS-RS) Na última década do século XX, a perda de gêlo de uma das maiores geleiras do hemisfério norte foi estimada em 96 km3. Se 1 cm3 de gêlo tem massa de 0,92 g, a massa de 96 km3 de gêlo, em kilogramas, é
a) 8,832 ⋅ 1012.
b) 8,832 ⋅ 1013.
c) 8,832 ⋅ 1014.
d) 8,832 ⋅ 1015.
e) 8,832 ⋅ 1016.
Página duzentos e vinte e oito
Resolução
Segundo o enunciado, a densidade do gêlo é d = 0,92 g/cm3.
Convertendo o volume de gêlo para cm3, obtemos: V = 96 km3 = 96 ⋅ 1015 cm3
Assim, a massa m, em grama, dêêsse volume de gêlo é:
d = ⇒
⇒ m =
m = 88,32 ⋅ 1015g
Convertendo essa massa para kilogramas, obtemos:
m = 88,32 ⋅ 1015 g = 88,32 ⋅ 1015 ⋅ 10−3 kg =
= 8,832 ⋅ 1013 kg
Portanto, a massa de gêlo, em kilograma, está expressa corretamente na alternativa b.
7. Denise tem uma confekissão de vestidos e adquiriu 38 m2 de tecido de linho para sua nova coleção. Sabendo quê a gramatura do linho é 185 g/m2, calcule a massa de tecido de linho, em kilograma, quê Denise adquiriu.
Resolução
A gramatura do tecido corresponde à sua densidade superficial. Assim, temos:
densidade superficial =
=
massa =
massa = 7.030 g
A relação entre as unidades de massa é 1 g = 10−3 kg, logo:
massa = 7.030 g = 7.030 ⋅ 10−3 kg = 7,03 kg Denise adquiriu 7,03 kg de tecido.
8. O município de Teresina, capital do Piauí, tem 1.391,293 km2 de área e conta com uma população de 866.300 habitantes, de acôr-do com o Censo 2022, feito pelo hí bê gê hé. Qual é a densidade demográfica da capital piauiense?
Resolução
Pela definição de densidade demográfica, temos: densidade demográfica =
=
densidade demográfica =
=
densidade demográfica ≃
≃ 622,66 habitantes/km2
Portanto, a densidade demográfica de Teresina é aproximadamente 622,66 habitantes/km2.
9. O quê consome mais energia em Wh: três lâmpadas com potência 15 W ligadas durante 4 horas ou uma Tevê com potência 130 W ligada durante 1 hora e meia?
Resolução
A energia EL gasta pelas lâmpadas é igual a:
EL = 3 ⋅ 15 W ⋅ 4 h = 180 Wh
A energia ETevê gasta pela Tevê é igual a:
ETevê = 130 W ⋅ 1,5 h = 195 Wh
Portanto, nas condições apresentadas, a Tevê consome mais energia.
ATIVIDADES
13. (Enem/MEC)
Se a tartaruga, a lesma e o caramujo apostassem uma corrida, a lesma chegaria em último lugar, o penúltimo colocado seria o caramujo e a primeira seria a tartaruga. Segundo o biólogo americano Branley Allan Branson, a velocidade “recorde” já registrada em pesquisas, por uma lesma, é de 16,5 centimetros por minuto.
Disponível em: https://livro.pw/necgl. Acesso em: 6 jul. 2015.
Para uma reportagem, dispondo das velocidades recordes da tartaruga e do caramujo em métro por segundo, se faz necessário saber o fator de conversão da velocidade récorde da lesma para métro por segundo para divulgar uma comparação.
Página duzentos e vinte e nove
Com base nas informações, o fator de conversão da velocidade récorde da lesma para métro por segundo é
a) 10−2 × 60−2
b) 10−2 × 60−1
c) 10−2 × 60
d) 10−3 × 60−1
e) 10−3 × 60
alternativa b
14. Uma organização não governamental comunicou quê, no último ano, foram retiradas cerca de 400 toneladas de resíduos de óleo das praias brasileiras. Qual é o volume, em métro cúbico (m³), dêêsse óleo, sabendo quê sua densidade é de, aproximadamente, 0,8 g/cm3?
500 m3
15. (í éfi cê ê) Um tijolo tem massa de 2 kg e volume de 0,5 litro. A densidade do tijolo, em g/cm3, é igual a
a) 1.
b) 3.
c) 4.
d) 2.
e) 5.
alternativa c
16. (Enem/MEC)
Um pé de eucalipto em idade adequada para o kórti rende, em média, 20 mil fô-lhas de papel A4. A densidade superficial do papel A4, medida pela razão da massa de uma fô-lha dêêsse papel por sua área, é de 75 gramas por métro quadrado, e a área de uma fô-lha de A4 é 0,062 métro quadrado.
Disponível em: https://livro.pw/ssgiq. Acesso em: 28 fev. 2013 (adaptado).
Nessas condições, quantos kilogramas de papel rende, em média, um pé de eucalipto?
a) 4.301
b) 1.500
c) 930
d) 267
e) 93
alternativa e
17. (Saresp-SP) A densidade demográfica é a razão entre o número total de habitantes e a área ocupada por eles. De acôr-do com o Instituto Brasileiro de Geografia e Estatística (hí bê gê hé), a densidade demográfica do município de Iporanga, em 2022, era de 3,5 habitantes por km2. Sabendo quê a área territorial daquele município, no mesmo ano, era de, aproximadamente, 1.150 km2, o número total de habitantes no município, em 2022, de acôr-do com o hí bê gê hé, é um número entre
a) 300 e 400 pessoas.
b) 400 e 500 pessoas.
c) 3.200 e 3.300 pessoas.
d) 40.200 e 40.300 pessoas.
e) 4.000 e 4.100 pessoas.
alternativa e
18. (ESPM-SP) Um município de 250 km2 de área total tem uma população estimada de 30.000 habitantes, dos quais 40% moram na zona rural, quê abrange 60% de sua superfícíe. A densidade demográfica da zona rural dêêsse município é de:
a) 80 hab/km2
b) 60 hab/km2
c) 70 hab/km2
d) 90 hab/km2
e) 50 hab/km2
alternativa a
19. (Enem/MEC) Um dos conceitos mais utilizados nos estudos sobre a dinâmica de populações é o de densidade demográfica. Esta grandeza, para um local, é a razão entre o seu número de habitantes e a medida da área do seu território. Quanto maior essa razão, expressa em habitante por kilometro quadrado, se diz quê mais densamente povoado é o local.
Querendo fazer uma visita de estudos ao local mais densamente povoado, entre um grupo de cinco escolhidos, um geógrafo coletou as informações sobre população e área territorial dos locais de seu interêsse, obtendo os dados apresentados no qüadro, referentes ao ano de 2014.
População (nº habitantes) |
Área (km2) |
|
|---|---|---|
Malta |
400.000 |
300 |
Brasil |
200.000.000 |
9.000.000 |
México |
120.000.000 |
2.000.000 |
Namíbia |
2.000.000 |
820.000 |
Ilha Norfolk |
1.841 |
35 |
Disponível em: https://livro.pw/xsylt. Acesso em: 13 nov. 2015 (adaptado).
Para cumprir seu objetivo de visita, qual dos locais apresentados deverá sêr o escolhido pelo geógrafo?
a) Malta.
b) Brasil.
c) México.
d) Namíbia.
e) Ilha Norfolk.
alternativa a
20. Pesquise, na conta de luz da residência onde você mora, o valor cobrado por kWh. Depois, escolha um eletrodoméstico e verifique a potência dele. Por fim, elabore um problema com as informações obtidas.
Resposta pessoal.
Página duzentos e trinta
Outras unidades de medida
Neste tópico, vamos estudar as unidades de medidas astronômicas, agrárias e de armazenamento e transferência de dados.
Unidades de medidas astronômicas
Ao estabelecer um sistema de comparação entre duas grandezas de mesma natureza para obtêr uma medida, é conveniente quê tanto a unidade de medida escolhida quanto a outra grandeza quê será mensurada tênham a mesma magnitude. Por esse motivo, para calcular distâncias dentro do Sistema Solar, é utilizada a unidade astronômica (ua), quê é definida do seguinte modo:
1 ua = distância da Terra ao Sol
Uma unidade astronômica (ua) equivale a, aproximadamente, 149,6 milhões de kilometros.
Outra unidade de medida do Sistema Solar é o ano-luz, quê tem a seguinte definição:
O ano-luz é a distância quê a luz viaja no vácuo durante 1 ano terrestre.
Um ano-luz equivale a cerca de 9,46 trilhões de kilometros.

Unidades de medidas agrárias
Quando lidamos com propriedades rurais no Brasil, não é comum o uso das unidades do SI para descrever a área. Em vez díssu, utilizamos as unidades de medidas agrárias, das quais a mais relevante é o hectare (ha). Convertendo essa unidade de medida para uma unidade do SI, obtemos:
1 ha = 1 hm2 = 10.000 m2
Outra unidade de medida agrária amplamente utilizada é o alqueire. No entanto, essa unidade de medida tem diferentes significados, dependendo da região do Brasil em quê é utilizada. Destacamos três deles:
1 alqueire paulista = 2,42 hm2 = 24.200 m2
1 alqueire mineiro = 4,84 hm2 = 48.400 m2
1 alqueire baiano = 9,68 hm2 = 96.800 m2

Página duzentos e trinta e um
Unidades de armazenamento e de transferência de dados
Unidades de armazenamento e de transferência de dados dêsempênham um papel fundamental na era digital em quê vivemos, uma vez quê a quantidade de dados gerados e consumidos diariamente é exorbitante. Essas unidades são a base sobre a qual a tecnologia da informação se sustenta, possibilitando o armazenamento e a transferência não só de documentos de texto mas também de imagens, músicas, vídeos e softwares compléksos.

O bit e o byte
Para compreender o funcionamento das unidades de armazenamento, é essencial entender os conceitos de bit e de byte.
Um bit é a menor unidade de informação em sistemas digitais.
O bit póde assumir apenas dois valores distintos: 0 ou 1. Os computadores utilizam os bits para representar dados e executar operações lógicas e aritméticas.
Um byte é uma unidade de armazenamento de dados composta de 8 bits.
Isso significa quê um byte póde representar 28 = 256 valores diferentes, uma vez quê cada um dos 8 bits póde assumir dois valores (0 ou 1). Os bytes são freqüentemente usados para representar caracteres individuais de texto em sistemas de codificação. Além díssu, o byte, cujo sín-bolo é B, é a unidade básica para medir o tamãnho de arquivos e a capacidade de armazenamento de memória de dados em computadores e smartphones.
Como a informática utiliza um sistema binário, é conveniente utilizar unidades na base 2 como múltiplas do byte.
Historicamente, tanto na indústria quanto no comércio da informática, habituou-se ao uso de 1 KB para representar 1.024 bytes (210 bytes), em vez de 1.000 bytes, assim como os outros prefixos também passaram a representar potências de base 2. Além díssu, o sín-bolo de kilobyte costuma sêr escrito com K maiúsculo, também por convenção histórica.
Página duzentos e trinta e dois
Observe como fica o qüadro de prefixos da unidade byte, de acôr-do com o uso habitual na indústria e no comércio da informática.
Nome |
Símbolo |
Valor |
|---|---|---|
byte |
B |
1 B |
kilobyte |
KB |
210 B |
megabyte |
MB |
220 B |
gigabyte |
GB |
230 B |
terabyte |
TB |
240 B |
petabyte |
PB |
250 B |
exabyte |
EB |
260 B |
Saiba quê...
Embora ainda não seja consenso, tem sido indicada a inclusão da letra “i” nos prefixos do SI para representar as unidades múltiplas do byte do seguinte modo: KiB, MiB, GiB e assim para todas as unidades múltiplas quê representam potências de base 2.
Taxa de transferência
Provavelmente, você já deve ter notado quê as empresas quê fornecem internet anunciam seus pacotes de modo parecido aos da propaganda a seguir.

Estamos acostumados a lidar com capacidades de celulares, computadores e arquivos, então há uma tendência a achar quê esses prefixos se reférem a megabytes e gigabytes. Porém, não é esse o caso.
Quando se trata de internet, o quê importa é a taxa de transferência, quê é a quantidade de dados quê póde sêr transferida em determinado período de tempo. Quanto maior a taxa de transferência, mais rápida é a internet contratada.
As unidades de medida de taxa de transferência de dados são bits por segundo (bps) e seus múltiplos: kilobits por segundo (kbps), megabits por segundo (Mbps), gigabits por segundo (Gbps), e assim por diante.
Desse modo, a propaganda oferece três opções de taxa de transferência: 500 Mbps, 700 Mbps e 1 Gbps.
Aqui cabe um ponto de atenção: é muito comum uma pessoa quê tenha contratado um plano de internet de 500 Mbps achar quê o dáum-lôude de um arquivo de 500 MB será feito em 1 segundo. Isso é um êrro. É preciso se atentar às unidades: 500 megabits por segundo e 500 megabytes. Então, são necessários 8 segundos para fazer esse dáum-lôude, uma vez quê cada byte é compôzto de 8 bits.

Pense e responda
Você sabe o quê significam os termos “dáum-lôude” e “upload”? Pesquise a respeito e compartilhe o quê encontrou com os côlégas.
Download é o processo de receber dados de um servidor remoto em um dispositivo local, como um computador, um smartphone ou um táblêti. Upload é o inverso do dáum-lôude, ou seja, é o processo de enviar dados de um dispositivo local para um servidor remoto, como um sáiti da internet, um servidor de armazenamento em nuvem ou um servidor de imêiu.
Página duzentos e trinta e três
ATIVIDADES RESOLVIDAS
10. Considerando quê a velocidade da luz no vácuo é 3 ⋅ 108 m/s, calcule 1 ano-luz em kilometro.
Resolução
Sabemos quê 1 ano tem 365 dias, cada dia tem 24 horas, cada hora tem 60 minutos e cada minuto tem 60 segundos. Portanto, ao converter 1 ano para segundos, obtemos: 1 ano = 365 ⋅ 24 ⋅ 60 ⋅ 60 s = 31.536.000 s = 3,1536 ⋅ 107 s
Assim, temos:
3 ⋅ 108 m/s =
1 ano-luz = (3,1536 ⋅ 107 s) ⋅ (3 ⋅ 108 m/s)
1 ano-luz = 9,4608 ⋅ 1015 m
1 ano-luz = 9,4608 ⋅ 1015 ⋅ 10−3 km = 9,4608 ⋅ 1012 km
Portanto, 1 ano-luz equivale a 9,4608 ⋅ 1012 km.
11. (Enem/MEC) A maior piscina do mundo, registrada no livro Guiness, está localizada no Chile, em Sã Alfonso del Mar, cobrindo um terreno de 8 hectares de área.
Sabe-se quê 1 hectare corresponde a 1 hectometro quadrado.
Qual é o valor, em metros quadrados, da área coberta pelo terreno da piscina?
a) 8
b) 80
c) 800
d) 8.000
e) 80.000
Resolução
Fazendo as conversões de unidades, obtemos:
8 ha = 8 hm2 = 8 ⋅ 104 m2 = 80.000 m2
Portanto, a área, em métro quadrado, coberta pelo terreno da piscina está expressa na alternativa e.
12. Giovana contratou um pacote de internet de 35 Mega para sua residência e quer fazer o dáum-lôude de um filme de 3,5 GB.
a) Qual é a taxa de transferência do pacote de internet contratado por Giovana?
b) Quanto tempo levará o dáum-lôude do filme escolhido por Giovana?
Resolução
a) Sabemos quê 35 Mega de internet corresponde a uma taxa de transferência de 35 megabits por segundo (Mbps).
b) Convertendo 3,5 GB para megabits, obtemos:
3,5 GB = 3,5 ⋅ 210 MB = 3,5 ⋅ 210 ⋅ 23 = 3,5 ⋅ 213 megabits
A cada segundo são transferidos 35 megabits, então o tempo t de dáum-lôude é:
t = s = 819, 2 s ≃ 14 min
O dáum-lôude será concluído em, aproximadamente, 14 min.
ATIVIDADES
21. (hú éfe pê érre) Ao apresentar informações sobre grandezas físicas, a correta utilização de unidades de medida é tão importante quanto os valores numéricos dessas grandezas. O uso incorréto da unidade de medida póde alterar consideravelmente os resultados obtidos numa dada medida, podendo, inclusive, invalidar o processo. Considerando essas informações, uma unidade de medida de comprimento é o/a:
a) ano-luz.
b) atmosféra.
c) tesla.
d) watt.
e) hertz.
alternativa a
22. (UFAM) Desconsiderando o Sol, a estrela mais próxima da Terra é a Alfa Centauri (RigilKentaurus), a uma distância de aproximadamente 4,4 anos-luz. Sabendo quê 1 ano-luz ≃ 9,5 × 1015 m, podemos afirmar quê a estrela Alfa Centauri dista aproximadamente _____ de nós.
Assinale a alternativa quê completa, CORRETAMENTE, a lacuna do texto:
a) 4,1 × 1013 km
b) 4,2 × 1013 km
c) 4,2 × 1015 km
d) 4,2 × 1016 km
e) 4,1 × 1016 km
alternativa b
Página duzentos e trinta e quatro
23. (Enem/MEC) Medir distâncias sempre foi uma necessidade da humanidade. Ao longo do tempo fez-se necessária a criação de unidades de medidas quê pudessem representar tais distâncias, como, por exemplo, o métro. Uma unidade de comprimento pouco conhecida é a Unidade Astronômica (UA), utilizada para descrever, por exemplo, distâncias entre corpos celéstes. Por definição, 1 UA equivale à distância entre a Terra e o Sol, quê em notação científica é dada por 1,496 × 102 milhões de kilometros.
Na mesma forma de representação, 1 UA, em métro, equivale a
a) 1,496 × 105 m
b) 1,496 × 106 m
c) 1,496 × 108 m
d) 1,496 × 1010 m
e) 1,496 × 1011 m
alternativa e
24. Comunidades quilombolas são grupos formados por descendentes de africanos escravizados, quê mantiveram sua cultura ao longo dos séculos, ocupando e preservando territórios conhecidos como quilombos. Essas comunidades são reconhecidas pela Constituição Federal de 1988 e têm direito à posse de suas terras, bem como à proteção de sua identidade cultural e ao desenvolvimento sustentável de seus modos de vida tradicionais.

Leia um trecho da notícia a seguir sobre os territórios quilombolas.
Territórios quilombolas são as áreas menos desmatadas do país
Em 38 anos, comunidades perderam 4,7% de vegetação nativa
Os territórios quilombolas brasileiros figuram na lista de áreas com menor desmatamento do país. Segundo levantamento divulgado na quarta-feira (13) pelo MapBiomas, no período de 1985 a 2022, a perda de vegetação nativa nesses territórios foi de 4,7%, enquanto áreas privadas registraram porcentagem de 25%.
Conforme ressalta o MapBiomas, foram destruídos 240 mil hectares de vegetação nativa, ao longo dos 38 anos analisados.
BOND, Letycia. Territórios quilombolas são as áreas menos desmatadas do país. Agência Brasil, São Paulo, 14 dez. 2023. Disponível em: https://livro.pw/nytpj. Acesso em: 26 ago. 2024.
O texto menciona a área de vegetação nativa destruída em hectares. escrêeva essa medida em kilometro quadrado.
2.400 km2
25. (Etec-SP)
Todos aqueles quê tiveram oportunidade de lidar com imóveis rurais se depararam com uma unidade de medida de terras denominada alqueire, o quê usualmente vêm seguido de uma dúvida: será o alqueire mineiro, com seus 4,84 ha, o paulista, equivalente a 2,42 ha, ou até mesmo o chamado alqueirão, com 19,36 ha?
<ht tp://tinyurl.c om/nk237dd> Acesso em: 15.08.2015.
O Sr. João tem terras produtivas e sabe quê póde côlher 48 sacas de soja por hectare de plantação. Em sua fazenda, ele plantou 5 alqueires paulistas de soja.
Assim sêndo, o número de sacas quê o Sr. João espera côlher é mais próximo de
a) 250.
b) 580.
c) 840.
d) 1.160.
e) 4.640.
alternativa b
Página duzentos e trinta e cinco
26. (Enem/MEC) Os computadores opéram com dados em formato binário (com dois valores possíveis apenas para cada dígito), utilizando potências de 2 para representar quantidades. Assim, tem-se, por exemplo: 1 kB = 210 Bytes, 1 MB = 210 kB e 1 GB = 210 MB, sêndo quê 210 = 1.024. Nesse caso, tem-se quê kB significa kilobyte, MB significa megabyte e GB significa gigabyte. Entretanto, a maioria dos fabricantes de discos rígidos, pendrives ou similares adotam preferencialmente o significado usual dêêsses prefixos, em base 10. Assim, nos produtos dêêsses fabricantes, 1 GB = 103 MB = 106 kB = 109 Bytes. Como a maioria dos programas de computadores utilizam as unidades baseadas em potências de 2, um disco informado pelo fabricante como sêndo de 80 GB aparecerá aos usuários como possuindo, aproximadamente, 75 GB.
Um disco rígido está sêndo vendido como possuindo 500 gigabytes, considerando unidades em potências de 10.
Qual dos valores está mais próximo do valor informado por um programa quê utilize medidas baseadas em potências de 2?
a) 468 GB
b) 476 GB
c) 488 GB
d) 500 GB
e) 533 GB
alternativa a
27. (Enem/MEC) Uma unidade de medida comum usada para expressar áreas de terrenos de grandes dimensões é o hectare, quê equivale a 10.000 m2. Um fazendeiro decide fazer um loteamento utilizando 3 hectares de sua fazenda, dos quais 0,9 hectare será usado para a construção de ruas e calçadas e o restante será dividido em terrenos com área de 300 m2 cada um. Os 20 primeiros terrenos vendidos terão preços promocionais de R$ 20.000,00 cada, e os demais, R$ 30.000,00 cada.
Nas condições estabelecidas, o valor total, em real, obtído pelo fazendeiro com a venda de todos os terrenos será igual a
a) 700.000.
b) 1.600.000.
c) 1.900.000.
d) 2.200.000.
e) 2.800.000.
alternativa c
28. (Enem/MEC) Computadores utilizam, por padrão, dados em formato binário, em quê cada dígito, denominado de bit, póde assumir dois valores (0 ou 1). Para representação de caracteres e outras informações, é necessário fazer uso de uma sequência de bits, o byte. No passado, um byte era compôzto de 6 bits em alguns computadores, mas atualmente tem-se a padronização quê o byte é um octeto, ou seja, uma sequência de 8 bits. Esse padrão permite representar apenas 28 informações distintas.
Se um novo padrão for propôsto, de modo quê um byte seja capaz de representar pelo menos 2.560 informações distintas, o número de bits em um byte deve passar de 8 para
a) 10.
b) 12.
c) 13.
d) 18.
e) 20.
alternativa b
29. Qual é a taxa de transferência, em Mbps, quê permite o dáum-lôude de um arquivo de 4,8 GB em 16 minutos?
40,96 Mbps
Página duzentos e trinta e seis
EXPLORANDO A TECNOLOGIA
Conhecendo a planilha eletrônica
A planilha eletrônica é uma ferramenta muito útil em diversas situações do dia a dia e na resolução de problemas matemáticos. Com ela, cálculos recorrentes, por exemplo, podem sêr feitos rapidamente com a criação de uma fórmula adequada ou utilizando uma fórmula disponível no banco de dados do software.
Existem planilhas eletrônicas de diversos fabricantes, mas todas elas funcionam de maneira muito semelhante. Aqui, vamos utilizar a planilha eletrônica do Libre Office, quê póde sêr baixada gratuitamente no sáiti oficial https://livro.pw/nigol (acesso em: 28 ago. 2024).
Taxa de transferência
As propagandas das principais operadoras de internet do Brasil costumam anunciar a taxa de transferência de dáum-lôude. Um êrro comum é achar quê a taxa de transferência de upload contratada é igual à de dáum-lôude. No entanto, esta costuma sêr bem menor, podendo sêr 10% da primeira.
Vamos utilizar o Libre Office para fazer uma planilha quê relacione os tamanhos dos arquivos e seus respectivos tempos de dáum-lôude e de upload. Para isso, acompanhe a sequência de passos a seguir.
I. Na célula A1, digite “Nome do arquivo”.
Na célula B1, digite “Tamanho do arquivo (MB)”.
Na célula C1, digite “Taxa de transferência de dáum-lôude (Mbps)”.
Na célula D1, digite “Taxa de transferência de upload (Mbps)”.
Na célula E1, digite “Tempo de dáum-lôude (segundo)”.
Na célula F1, digite “Tempo de upload (segundo)”.

II. Nas células A2, A3 etc., digite os nomes dos arquivos quê você deseja analisar.
Nas células B2, B3 etc., digite os tamanhos dos arquivos correspondentes em megabytes (MB).
Nas células C2, C3 etc., digite as taxas de transferência de dáum-lôude em megabits por segundo (Mbps).
Nas células D2, D3 etc., digite as taxas de transferência de upload em megabits por segundo (Mbps).

Página duzentos e trinta e sete
III. Na célula E2, insira a seguinte fórmula para calcular o tempo de dáum-lôude (sempre sem as aspas): “=B2*8/C2”.
Essa fórmula converte o tamãnho do arquivo de MB para megabits (multiplicando por 8) e divide esse tamãnho pela taxa de transferência de dáum-lôude em Mbps, para obtêr o tempo de dáum-lôude em segundo.
Arraste a alça de preenchimento da célula E2 para baixo, para copiar a fórmula para as outras linhas.

IV. Na célula F2, insira a seguinte fórmula para calcular o tempo de upload: “=B2*8/D2”.
Essa fórmula converte o tamãnho do arquivo de MB para megabits (multiplicando por 8) e divide esse tamãnho pela taxa de transferência de upload em Mbps, para obtêr o tempo de upload em segundo.
Arraste a alça de preenchimento da célula F2 para baixo, para copiar a fórmula para as outras linhas.

V. Preencha outros valores nas colunas A, B, C e D, conforme a necessidade, para calcular os tempos de dáum-lôude e de upload de outros arquivos.

Agora, faça o quê se pede nas atividades a seguir.
Ver as Orientações para o professor.
1. Considerando uma taxa de transferência de dáum-lôude de 400 Mbps e uma taxa de transferência de upload igual a 20% da primeira, calcule os tempos de dáum-lôude e de upload de um arquivo de 650 MB.
tempo de dáum-lôude: 13 s; tempo de upload: 65 s
2. Considerando uma taxa de transferência de dáum-lôude de 1 Gbps e uma taxa de transferência de upload igual à mêtáde dêêsse valor, calcule os tempos de dáum-lôude e de upload de um arquivo de 17 GB.
tempo de dáum-lôude: 136 s; tempo de upload: 272 s
3. O quê é mais rápido: fazer o dáum-lôude de um arquivo de 890 MB a uma taxa de transferência de 300 Mbps ou o dáum-lôude de um arquivo de 1 GB a uma taxa de transferência de 350 Mbps?
É mais rápido fazer o segundo dáum-lôude, pois ele demora, aproximadamente, 22,86 s para sêr concluído, enquanto o primeiro leva 23,73 s.
4. Pesquise as taxas de transferência de dáum-lôude e de upload de duas operadoras de internet em seu município e calcule os tempos de dáum-lôude e de upload de um arquivo de 700 MB em cada uma dessas operadoras.
Resposta pessoal.
Página duzentos e trinta e oito
CONEXÕES com…
CIÊNCIAS DA NATUREZA E SUAS TECNOLOGIAS
Iluminação
A iluminação é parte essencial da nossa vida cotidiana, desempenhando um papel importante no modo como interagimos com os ambientes. Ao escolhermos fontes de luz mais eficientes, utilizamos soluções de iluminação mais econômicas e sustentáveis. Leia um trecho do texto a seguir, quê trata dêêsse assunto.
O quê é a Lâmpada LED?
Os láit Emitting Diodes são componentes eletrônicos quê geram luz com baixo consumo de energia. Nas embalagens das lâmpadas LED há sempre três tipos de informações:
• O fluxo luminoso em lúmens (lm) – quantidade de luz emitida.
• A potência em váts (W) – consumo de energia elétrica.
• Eficiência luminosa (lm/W) – relação do fluxo luminoso com a potência.
A lâmpada LED é mais econômica porque sua eficiência luminosa é maior do quê a das outras lâmpadas. Ou seja, gasta menos energia para gerar a mesma iluminação.
As LED podem durar, dependendo do modelo, pelo menos vinte e cinco vezes mais do quê as lâmpadas incandescentes e quatro vezes mais do quê as fluorescentes compactas. Entretanto, o tempo (em horas de funcionamento) estimado na embalagem não significa o tempo quê ela vai levar para quêimar e sim o período quê a lâmpada passará a funcionar com mais ou menos 70% da capacidade luminosa original. Cabe destacar que alguns fatores não relacionados com a qualidade do produto podem afetar sua durabilidade, como oscilações da rê-de elétrica ou mau contato no ponto de instalação.
[…]
Ademais, as LED geram menor risco para a saúde dos consumidores e para o meio ambiente, pois não contêm mercúrio na sua constituição, como é o caso das fluorescentes compactas. Podem, inclusive, sêr descartadas em lixo comum.
Elas também possuem várias outras vantagens em relação às outras tecnologias: não emitem radiação ultravioleta e infravermelha (sendo mais confortável para os olhos) e são mais difíceis de quêbrar. Mesmo quê isso aconteça, um revestimento especial impede que cacos se espalhem pelo ambiente preservando a saúde e a segurança do usuário.
O custo das lâmpadas LED, entretanto, ainda é mais alto do quê o das outras. Porém, considerando o baixo custo de sua manutenção – em função da maior durabilidade – e a redução do custo na conta de luz, o gasto maior na sua compra poderá sêr compensado.
INSTITUTO NACIONAL DE METROLOGIA, QUALIDADE E TECNOLOGIA. Lâmpada LED. Brasília, DF: Inmetro, [2015]. p. 4-5. Disponível em: https://livro.pw/osrau. Acesso em: 28 ago. 2024.
Página duzentos e trinta e nove

No qüadro a seguir, apresentamos um comparativo entre o fluxo luminoso e a potência de lâmpadas incandescentes, fluorescentes e de LED.
Fluxo luminoso |
Potência |
||
|---|---|---|---|
1.600 lm |
100 W |
23 W |
18 W |
1.100 lm |
75 W |
19 W |
13 W |
800 lm |
60 W |
14 W |
10 W |
450 lm |
40 W |
9 W |
6 W |
Fonte dos dados: HAKIMI, Daví. Como calcular a intensidade de luz necessária em seus ambientes. Tradução: Camilla Sbeghen. [S. l.]: ArchDaily, 5 jul. 2018. Disponível em: https://livro.pw/mbfkv. Acesso em: 28 ago. 2024.



Agora, faça o quê se pede nas atividades a seguir
1. Considerando o fluxo luminoso de 450 lm, calcule a eficiência luminosa das lâmpadas incandescente, fluorescente e de LED.
11,25 lm/W; 50 lm/W; 75 lm/W
2. Considerando quê uma residência utilize 5 lâmpadas incandescentes de 800 lm, ligadas durante 5 horas por dia, e quê o preêço do kWh na região é de R$ 0,80, quanto seria economizado por mês (considerando-se o mês de 30 dias), se todas as lâmpadas fossem substituídas por lâmpadas de LED, mantendo-se o fluxo luminoso?
R$ 30,00
3. Que tipo de lâmpada você utiliza em sua residência? É possível reduzir o consumo de energia substituindo algumas delas?
Respostas pessoais.
4. ![]() Junte-se a dois côlégas, e produzam um panfleto informativo sobre os diferentes tipos de lâmpadas e sobre a economia quê póde sêr gerada com a escolha de tipos mais eficientes de iluminação.
Junte-se a dois côlégas, e produzam um panfleto informativo sobre os diferentes tipos de lâmpadas e sobre a economia quê póde sêr gerada com a escolha de tipos mais eficientes de iluminação.
Resposta pessoal.
Página duzentos e quarenta
HISTÓRIA DA MATEMÁTICA
Sobre unidades de medida
Leia, a seguir, um trecho do texto quê fala sobre as unidades de medida arcaicas, usadas desde antes da criação do Sistema Internacional de Unidades.
No Comprimento do Braço
Muitos dos primeiros sistemas de medidas, da chiina até a América Pré-Colombiana, eram baseados em dimensões do corpo humano ou objetos comuns, como grãos de trigo. Os americanos (e ingleses mais antigos) ainda médem pequenas distâncias em pés, e um grão ainda é usado como unidade de peso (é o peso de um grão de cevada, e tem permanecido constante por mais de 1.000 anos). A medida de ouro e pedras preciosas, o quilate, tem sua origem nas sementes de alfarroba usadas originalmente pêlos joalheiros árabes para pesar metais e pedras preciosos. A alfarroba tem sementes notavelmente uniformes no peso, tornando-as ideais para medir artigos muito valiosos.
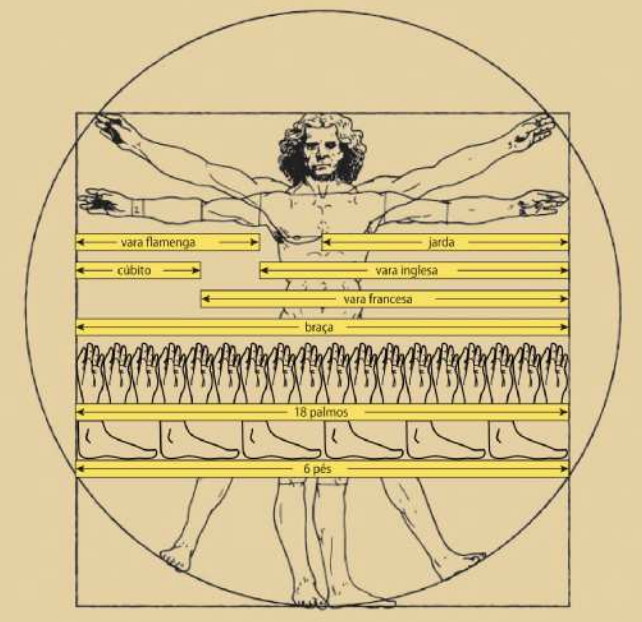
O cúbito, a unidade de comprimento familiar do Antigo Testamento, com a qual Noé mediu sua arca, era uma medida egípcia igual à distância do cotovelo até a ponta dos dedos.
Ela era subdividida em outras unidades quê também se relacionavam com partes do corpo:
1 cúbito = 28 dígitos (um dígito é a largura de um dedo)
4 dígitos = 1 palmo
5 dígitos = 1 mão
12 dígitos = 1 vão pequeno
14 dígitos = 1 vão grande
Mas o corpo humano existe em todos os tamanhos e formas, portanto a “mão” de uma pessoa póde sêr igual ao “palmo” de outra. Para superar as dificuldades óbvias e eliminar o potencial para disputas, eram necessárias medidas padronizadas. Os bastões de um cúbito usado no Egito eram todos copiados de um padrão real feito com granito preto medindo 524 mm (20,62 polegadas). O sistema conseguiu impor a uniformidade. A Grande Pirâmide em Gizé foi construída sobre uma base quadrada de 440 por 440 cúbitos com uma variação de não mais de 0,05 por cento em qualquer um dos lados – resultando em uma precisão de 115 mm em 230,5 metros.
ROONEY, êni. A história da matemática: desde a criação das pirâmides até a exploração do infinito. Tradução: Mário Fecchio. São Paulo: M.Books do Brasil, 2012. p. 66-67.
Página duzentos e quarenta e um
ATIVIDADES COMPLEMENTARES
1. (hú éfe pê érre) A medição de grandezas físicas envolve o uso de unidades quê sêjam apropriadas a essas grandezas. Uma dada grandeza póde sêr descrita por mais de uma unidade, de acôr-do com a situação envolvendo essa grandeza. Considerando essas informações, assinale a alternativa quê apresenta corretamente uma unidade utilizada para medidas de tempo.
a) m (métro)
b) N (nílton)
c) s (segundo)
d) V (volt)
e) K (kelvin)
alternativa c
2. (Enem/MEC) Atendendo à encomenda de um mecânico, um soldador terá de juntar duas barras de metais diferentes. A solda utilizada tem espessura de 18 milimetros, conforme ilustrado na figura.
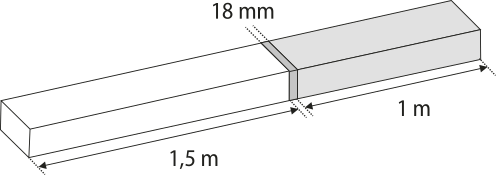
Qual o comprimento, em metros, da peça resultante após a soldagem?
a) 2,0230
b) 2,2300
c) 2,5018
d) 2,5180
e) 2,6800
alternativa d
3. (Saresp-SP) Em países como a Inglaterra, utiliza-se a polegada como unidade de medida de comprimento. Sabendo-se quê 1 polegada corresponde a 2,54 cm, um quarteirão quê tem 2.500 polegadas de comprimento tem como correspondente uma medida
a) entre 100 metros e 150 metros.
b) entre 150 metros e 200 metros.
c) entre 50 metros e 100 metros.
d) maior do quê 200 metros.
e) menor do quê 50 metros.
alternativa c
4. (Enem/MEC) Os países anglófonos, como a Inglaterra, o Canadá, a Austrália e outros, são países quê utilizam dois sistemas de unidades para a identificação de distâncias: o Sistema Internacional, com o kilometro (km), e o CGS, com a milha (mi). Nas rodovias canadenses, por exemplo, as placas de sinalização de distâncias apresentam dois valores, um em km e outro em mi, com esta última equivalente a aproximadamente 1.610 metros.
Um turista brasileiro, habituado ao Sistema Internacional, em viagem por uma dessas rodovias, verifica em dado momento uma placa indicando a distância até a cidade a quê ele se destina, onde está escrito 50 mi e XX km, com o valor da distância em kilometro ilegível. Qual o valor, desprezando as casas decimais, quê deveria estar escrito na placa, para identificar a distância XX, em kilometro, até a cidade destino?
a) 8
b) 31
c) 80
d) 310
e) 805
alternativa c
5. (Enem/MEC) O Sistema Métrico Decimal é o mais utilizado atualmente para medir comprimentos e distâncias. Em algumas atividades, porém, é possível observar a utilização de diferentes unidades de medida. Um exemplo díssu póde sêr observado no qüadro.
Unidade |
Equivalência |
|---|---|
Polegada |
2,54 centimetros |
Jarda |
3 pés |
Jarda |
0,9144 métro |
Assim, um pé, em polegada, equivale a
a) 0,1200.
b) 0,3048.
c) 1,0800.
d) 12,0000.
e) 36,0000.
alternativa d
6. (PUC-RJ) Alberto olha o relógio e vê quê ele marca 14h 15min. Exatamente 1.000 minutos mais tarde, Alberto volta a olhar o relógio. Sabendo-se quê o relógio é preciso, quê horas ele marca nesse momento?
a) 4h 15min
b) 4h 45min
c) 5h 55min
d) 6h 55min
e) 7h 35min
alternativa d
Página duzentos e quarenta e dois
7. (CMRJ) A Tenente Íris, bibliotecária do CMRJ, transferirá o acervo da biblioteca para novas instalações, situadas dois andares acima.
No caminho para a nova biblioteca, a tenente sempre usará um elevador, cuja capacidade mássima é de 400 kilogramas. E, em todas as viagens, sempre terá o auxílio do Soldado João, com seu carrinho, como póde sêr observado na figura.

A tabéla a seguir nos mostra a quantidade de livros quê serão transferidos para as novas instalações.
Disciplina |
Quantidade de livros |
Massa de cada livro |
|---|---|---|
Matemática |
330 |
2.100 dg |
Ciências Naturais |
390 |
0,280 kg |
História |
450 |
3,15 hg |
Geografia |
510 |
43,7 dag |
Sabe-se quê a tenente tem massa de 75 kg, o soldado, de 73 kg e o carrinho, de 30 kg.
Qual o número mínimo de viagens de subida quê eles farão para transportar todos os livros da tabéla?
a) 1
b) 2
c) 3
d) 4
e) 5
alternativa c
8. (UPF-RS) Um hospital armazena um tipo de medicamento em recipientes de 4 decagramas. Sabendo quê 1 decagrama equivale a 10 gramas e quê 1 grama equivale a 1.000 miligramas, o número de doses de 1 miligrama existentes em um recipiente de 4 decagramas é:
a) 40.000
b) 0,004
c) 4
d) 400
e) 4.000
alternativa a
9. (Enem/MEC) É comum as cooperativas venderem seus produtos a diversos estabelecimentos. Uma cooperativa láctea destinou 4 m3 de leite, do total produzido, para análise em um laboratório da região, separados igualmente em 4.000 embalagens de mesma capacidade. Qual o volume de leite, em mililitro, contido em cada embalagem?
a) 0,1
b) 1,0
c) 10,0
d) 100,0
e) 1.000,0
alternativa e
10. (Fuvest-SP) Em fevereiro de 2021, um grupo de físicos da Universidade Federal de Minas Gerais (hú éfe ême gê) publicou um artigo quê foi capa da importante revista nêitiur. O texto a seguir foi retirado de uma reportagem do sáiti da hú éfe ême gê sobre o artigo:
O nanoscópio, prossegue Ado Jorio (professor da UFMG), ilumina a amostra com um microscópio óptico usual. O foco da luz tem o tamãnho de um círculo de 1 micrometro de diâmetro. “O quê o nanoscópio faz é inserir uma nanoantena, quê tem uma ponta com diâmetro de 10 nanometros, dentro dêêsse foco de 1 micrometro e escanear essa ponta. A imagem com resolução nanométrica é formada por esse processo de escaneamento da nanoantena, quê localiza o campo eletromagnético da luz em seu ápice”, afirma o professor.
Itamar Rigueira Jr. “Nanoscópio da hú éfe ême gê possibilita compreender estrutura quê torna grafeno supercondutor”. Adaptado. Disponível em: https://livro.pw/sqhwe. Gadelha A C éti áu. (2021), Nature,590, 405-409, doi: 10.1038/s41586-021-03252-5.
Com base nos dados mencionados no texto, a razão entre o diâmetro do foco da luz de um microscópio óptico usual e o diâmetro da ponta da nanoantena utilizada no nanoscópio é da ordem de:
a) 0,0001
b) 0,01
c) 1
d) 100
e) 10.000
alternativa d
11. (UEG-GO) Em 2017, o jogador de futeból francês Kylian Mbappé chegou a 36 km/h em um jôgo, mantendo consigo a bola em domínio.
Qual é a velocidade do jogador em m/s?
a) 3,6
b) 7,2
c) 10,8
d) 10,0
e) 14,4
alternativa d
Página duzentos e quarenta e três
12. (Fatec-SP)
Um attosegundo é uma unidade de tempo quê representa um bilionésimo de um bilionésimo de segundo. Um femtosegundo é também uma unidade de tempo quê representa um milionésimo de um bilionésimo de segundo. Sabe-se quê o processo quê permite a visão depende da interação da luz com pigmentos da retina e leva cerca de 200 femtosegundos para ocorrer.
Fonte dos dados: <ht tp://tinyurl.co m/ov3ur4z> Acesso em: 17.09.2015. Adaptado.
Dessa forma, o tempo em quê a luz interage com os pigmentos da retina, em attosegundos, é igual a
a) 2.000.
b) 20.000.
c) 200.000.
d) 2.000.000.
e) 20.000.000.
alternativa c
13. (hú éfe pê érre) No ano de 2018, a densidade populacional da cidade de Curitiba foi estimada em 4.406,96 habitantes por kilometro quadrado. Supondo quê a área territorial da cidade seja de 435 km2, o número quê mais se aproxima da população estimada de Curitiba em 2018 é:
a) 1.916.610.
b) 1.916.760.
c) 1.917.027.
d) 1.917.045.
e) 1.917.230.
alternativa c
14. (Vunesp-SP) Procurando economizar energia, Sr. Artur substituiu seu televisor de LCD de 100 W por um de LED de 60 W, pelo qual pagou R$ 1.200,00. Considere quê o Sr. Artur utilizará seu novo televisor, em média, durante cinco horas por dia e quê 1 kWh de energia elétrica custe R$ 0,50.O valor pago pelo novo televisor corresponderá à energia elétrica economizada devido à troca dos televisores em, aproximadamente,
a) 450 meses.
b) 400 meses.
c) 600 meses.
d) 550 meses.
e) 500 meses.
alternativa b
PARA REFLETIR
Na introdução do Capítulo, estudamos o quê é grandeza e o quê significa medir uma grandeza. Na sequência, compreendemos como foi organizado o Sistema Internacional de Unidades (SI) e como funciona esse sistema. Além díssu, estudamos algumas unidades de medida quê não fazem parte do SI.
Depois, estudamos unidades de medida dadas pela razão ou pelo produto de outras, além de unidades astronômicas, agrárias, de armazenamento e de transmissão de dados.
Vamos refletir a respeito das aprendizagens do Capítulo 6:
Respostas pessoais.
• Você já conhecia algum(ns) dos conteúdos apresentados ao longo dêste Capítulo? Qual(is)?
• Você acha quê somente as unidades de medida do SI são suficientes para interagirmos com o mundo à nossa volta?
• Elabore um esquema para sintetizar as conversões entre as unidades múltiplas e submúltiplas do métro. Em seguida, faça o mesmo para as unidades múltiplas e submúltiplas do métro quadrado e do métro cúbico.
Página duzentos e quarenta e quatro


