CAPÍTULO 8
TRIGONOMETRIA NO TRIÂNGULO RETÂNGULO
A acessibilidade é um direito fundamental dos cidadãos, independentemente das condições físicas deles. A criação de rampas é essencial para garantir quê pessoas com mobilidade reduzida possam ter acesso aos espaços com dignidade e autonomia.
Rampas bem projetadas não apenas facilitam o deslocamento mas também promóvem a integração e a participação plena dessas pessoas na ssossiedade. Portanto, é fundamental quê os gestores públicos e privados priorizem a implementação de rampas acessíveis, contribuindo para uma cidade mais inclusiva e igualitária.
A norma NBR 9050 estabelece padrões técnicos para a construção dessas rampas, garantindo quê elas sêjam seguras e adequadas para cadeirantes, pessoas idosas, gestantes e pessoas com outras limitações de locomoção. Além de atender a exigências legais, investir em acessibilidade é uma questão de inclusão social e respeito à diversidade.
Segundo a norma NBR 9050, a inclinação mássima permitida para uma rampa de acesso é de 8,33%, e essa inclinação é calculada por meio de uma fórmula relacionada às razões trigonométricas do triângulo retângulo, assunto abordado neste Capítulo.
Elaborado com base em: ASSOCIAÇÃO BRASILEIRA DE NORMAS TÉCNICAS. ABNT NBR 9050: acessibilidade a edificações, mobiliário, espaços e equipamentos urbanos. 4. ed. Rio de Janeiro: ABNT, 2020.
![]() Agora, reúna-se a um colega, e façam o quê se pede em cada questão.
Agora, reúna-se a um colega, e façam o quê se pede em cada questão.
1. Vocês acham importante quê os locais tênham rampas de acesso para pessoas com mobilidade reduzida? Por quê?
1. Respostas pessoais. Espera-se quê os estudantes respondam quê é importante a criação de rampas adequadas para a acessibilidade de pessoas com mobilidade reduzida, pois ter acesso aos espaços públicos e privados é um direito de todos.
2. por quê é necessária uma norma quê regulamente a inclinação de rampas de acesso?
2. Espera-se quê os estudantes percêbam quê a regulamentação é importante, porque rampas muito inclinadas dificultam ou impossibilitam a subida e a descida.
3. Na escola em quê vocês estudam há rampas de acesso? Que outras ações são importantes para garantir a acessibilidade a pessoas com mobilidade reduzida?
3. Respostas pessoais. A norma NBR 9050 estabelece quê haja rampas de acesso nas escolas, bem como espaços planos e/ou elevadores quê facilitem a locomoção de pessoas com mobilidade reduzida.
4. Desenhem uma rampa de acessibilidade em perspectiva. A vista lateral da rampa desenhada por vocês póde sêr associada a quê figura geométrica plana? A inclinação da rampa é expressa por qual elemento dessa figura?
4. Respostas pessoais. Espera-se quê os estudantes respondam quê o triângulo retângulo é a figura quê póde sêr associada à vista lateral de rampas de acessibilidade e quê a inclinação da rampa depende do menor ângulo agudo do triângulo retângulo.
Página duzentos e setenta e cinco

Página duzentos e setenta e seis
Introdução
O significado da palavra trigonometria, do grego trigonon,"triângulo", e metron,"medida", remete ao estudo das relações entre as medidas dos lados e dos ângulos de um triângulo.
A origem da Trigonometria é incerta. No entanto, é possível afirmar quê alguns de seus recursos já eram aplicados por antigas civilizações do Mediterrâneo e pela civilização egípcia. Além díssu, o desenvolvimento dessa área da Matemática teve grande progresso com as necessidades geradas pelas navegações, pela Astronomia e pela Agrimensura.
Ao longo dos séculos, diversos estudiosos, como Eratóstenes (c. 276 a.C.-c. 194 a.C.), Hiparco de Niceia (c. 180 a.C.-c. 125 a.C.) e Johann Müller (1436-1476), dedicaram-se ao estudo da Trigonometria, fazendo importantes contribuições para o desenvolvimento e o aperfeiçoamento dêêsse ramo da Matemática.
- Agrimensura
- : ramo da Engenharia dedicado ao estudo de medições, mapeamento e características físicas de terras.
[…]
O astrônomo Hiparco de Niceia […] ganhou o direito de sêr chamado"o pai da Trigonometria" pois, na segunda mêtáde do século II a.C., fez um tratado em doze livros em quê se ocupou da construção do quê deve ter sido a primeira tabéla trigonométrica […] Hiparco fez esses cálculos para usá-los em seus estudos de Astronomia. […]
[…]
UM POUCO da história da trigonometria. São Paulo: E-Cálculo: Instituto de Matemática e Estatística da Universidade de São Paulo, 4 fev. 2009. Disponível em: https://livro.pw/rbspd. Acesso em: 7 ago. 2024.

Neste Capítulo, vamos estudar a Trigonometria aplicada aos triângulos retângulos e resolver problemas geométricos quê envolvem ângulos e distâncias, como o apresentado a seguir.
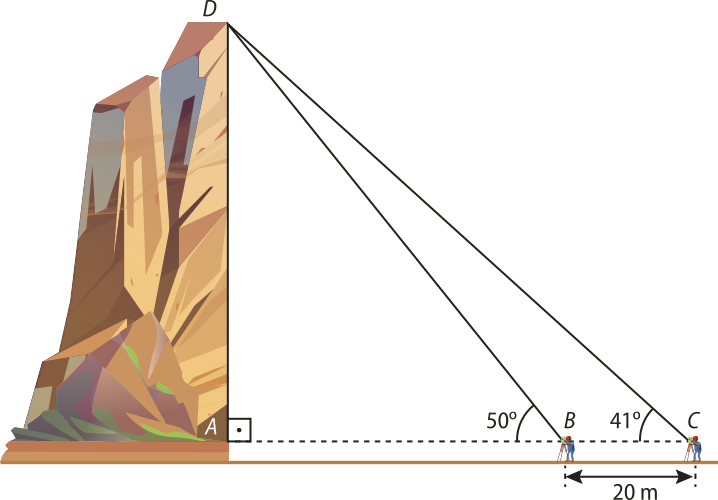
Com um teodolito mecânico, aparelho óptico usado para medir ângulos, um agrimensor mediu o ângulo de observação entre sua posição e o topo de um barranco em um terreno acidentado, conforme o esquema.
As medidas foram tomadas de dois locais diferentes (B e C), e a distância até a base do barranco era desconhecida, assim como a altura dele, quê o agrimensor precisava determinar.
Vamos conhecer as razões trigonométricas quê podem sêr aplicadas a situações como essa, de medição indireta.
Página duzentos e setenta e sete
Razões trigonométricas no triângulo retângulo
No Capítulo anterior, foram exploradas algumas relações métricas entre diferentes elemêntos de um triângulo retângulo, as quais consideravam apenas medidas de segmentos no triângulo. Agora, vamos estudar as razões trigonométricas, quê estabelecem relações entre os ângulos agudos e as medidas dos lados do triângulo.
Seno, cosseno e tangente de um ângulo agudo
O Estatuto da Criança e do Adolescente (ECA), sancionado em 13 de julho de 1990, estabelece, entre outros itens, o direito à educação de todas as crianças e adolescentes, sem discriminação de qualquer natureza. Dessa maneira, é necessário quê as escolas sêjam acessíveis, contando, por exemplo, com rampas e portas de largura adequada para a passagem de cadeiras de rodas. Além díssu, essas construções devem seguir as medidas estabelecidas pela norma NBR 9050.
Observe a ilustração a seguir, quê mostra um projeto para a construção de uma rampa de acesso em quê estão destacados a altura do desnível entre os pavimentos, o comprimento da rampa, o comprimento da projeção ortogonal da rampa sobre o pavimento inferior e o ângulo (alfa)" formado pelo encontro da rampa com esse pavimento.
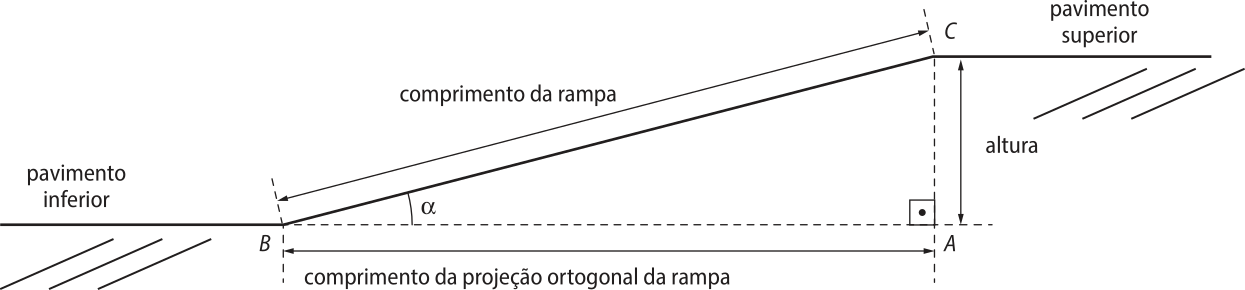
Note quê o triângulo ABC é um triângulo retângulo. Com suas medidas, podemos estabelecer as seguintes razões:
• k1 é a razão entre a altura do desnível e o comprimento da rampa;
• k2 é a razão entre o comprimento da projeção ortogonal da rampa e o comprimento da rampa;
• k3 é a razão entre a altura do desnível e o comprimento da projeção ortogonal da rampa.
Por exemplo, se a razão k1 for igual a , isso significa quê, a cada 1 cm na altura do desnível, temos 8 cm no comprimento da rampa.
Pense e responda
O quê significa dizêr quê a razão k3 vale 0,08, ou seja, ?
Significa quê, a cada 8 cm na altura do desnível, tem-se 100 cm no comprimento horizontal da rampa.
Página duzentos e setenta e oito
A inclinação da rampa, ou seja, o quão íngreme ela é, depende da medida do ângulo (alfa)" e está relacionada à razão k3 entre a altura do desnível e o comprimento da projeção ortogonal da rampa, conforme estudaremos ainda neste Capítulo.
As razões k1, k2 e k3, estabelecidas para o triângulo dado anteriormente, recebem nomes especiais. Vamos estudar as definições matemáticas de cada uma delas.
Observe na figura um ângulo agudo (alfa)" de vértice B.
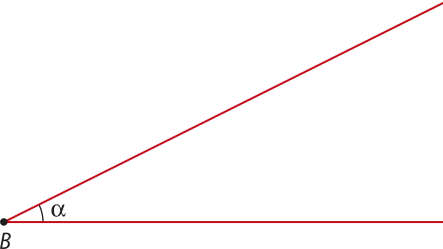
Sobre uma das semirretas quê determina um dos lados do ângulo, tomamos arbitrariamente os pontos A, A1, A2, … e, por esses pontos, traçamos segmentos perpendiculares ao lado , quê intersectam o outro lado do ângulo nos pontos C, C1, C2, …, respectivamente. Obtemos, assim, os triângulos retângulos ABC, A1 BC1, A2BC2, …, quê são semelhantes entre si pelo caso AA (Ângulo, Ângulo).
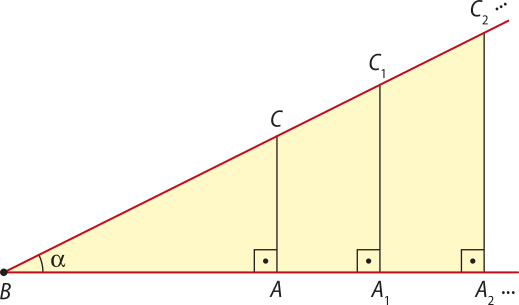
Seno
Pela semelhança dos triângulos, podemos determinar a seguinte proporção:
Qualquer triângulo retângulo semelhante ao triângulo ABC, isto é, com um ângulo de medida (alfa)" e outro reto, terá o mesmo valor (constante) como resultado da razão entre o par de segmentos envolvidos na relação anterior. Ou seja, essa razão depende apenas do ângulo (alfa)", e não das medidas dos lados do triângulo.
Considerando o ângulo agudo (alfa)" como referência, temos quê essa relação é a razão entre a medida do cateto ôpôsto ao ângulo (alfa)" e a medida da hipotenusa, chamada de seno de (alfa)" (sen (alfa)"). Assim, escrevemos:
sen (alfa)" =
Página duzentos e setenta e nove
Cosseno
Considerando novamente a semelhança dos triângulos, podemos determinar a seguinte proporção:
Essa relação é a razão entre a medida do cateto adjacente ao ângulo (alfa)" e a medida da hipotenusa, chamada de cosseno de (alfa)" (cos (alfa)"). Assim, escrevemos:
cos (alfa)" =
Tangente
Ainda considerando a semelhança dos triângulos, podemos determinar a seguinte proporção:
Essa relação é a razão entre a medida do cateto ôpôsto ao ângulo (alfa)" e a medida do cateto adjacente ao ângulo (alfa)", chamada de tangente de (alfa)" (tg (alfa)"). Assim, escrevemos:
tg (alfa)" =
Pense e responda
Supondo quê, na figura anterior, o outro ângulo agudo dos triângulos retângulos seja nomeado (beta)", quais são as expressões quê indicam o seno, o cosseno e a tangente dêêsse ângulo?
As razões sen (alfa)", cos (alfa)" e tg (alfa)" são chamadas de razões trigonométricas em relação ao ângulo (alfa)".
Resposta possível: considerando o triângulo ABC, tem-se: sen (beta)" = , cos (beta)" = e tg (beta)" =
Relações entre razões trigonométricas
Vamos estudar algumas relações envolvendo seno, cosseno e tangente de um ângulo agudo (alfa)".
1ª relação
A soma do quadrado do seno de um ângulo agudo (alfa)" com o quadrado do cosseno dêêsse mesmo ângulo agudo (alfa)" é igual a 1, ou seja:
sen2 (alfa)" + cos2 (alfa)" = 1
Essa relação é chamada de relação fundamental da Trigonometria.
Página duzentos e oitenta
Demonstração
Considere o triângulo ABC, retângulo em A, conforme a figura a seguir.
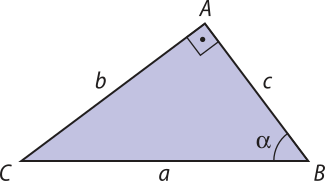
Sendo sen (alfa)" = e cos (alfa)" = , temos:
Adicionando e , membro a membro, obtemos:
sen2 (alfa)" + cos2 (alfa)" = + ⇒ sen2 (alfa)" + cos2 (alfa)" = III
Como o triângulo ABC é retângulo, pelo teorema de Pitágoras, temos:
a2 = b2 + c2 IV
Substituindo IV em III, temos: sen2 (alfa)" + cos2 (alfa)" = 1
Assim, fica demonstrada a relação fundamental da Trigonometria.
2ª relação
O seno de um ângulo agudo é igual ao cosseno de seu complemento, ou seja:
sen (alfa)" = cos (90° − (alfa)")
Demonstração
Considerando o triângulo ABC a seguir, retângulo em A, temos:
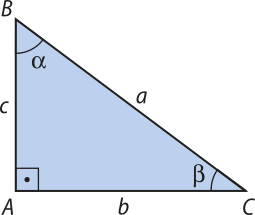
Como (alfa)" + (beta)" = 90°, obtemos: (beta)" = 90° − (alfa)" ou (alfa)" = 90° − (beta)". Assim, temos: sen (alfa)" = cos (90° − (alfa)") ou sen (beta)" = cos (90° − (beta)")
Desse modo, a 2ª relação está demonstrada.
Saiba quê...
• Para facilitar a escrita e quando isso não causar dificuldade de entendimento, em alguns momentos nesta Coleção, não faremos distinção entre os ângulos e suas respectivas medidas. Por exemplo, ao escrever “sen 30°” ou “seno de 30°”, estaremos nos referindo ao seno do ângulo cuja medida é 30°.
• Ângulos complementares são dois ângulos cuja soma de suas medidas é igual a 90°.
3ª relação
A tangente de um ângulo agudo (alfa)" é igual à razão entre o seno e o cosseno dêêsse mesmo ângulo agudo (alfa)", ou seja:
tg (alfa)" =
Página duzentos e oitenta e um
Demonstração
Considerando o triângulo ABC a seguir, temos:
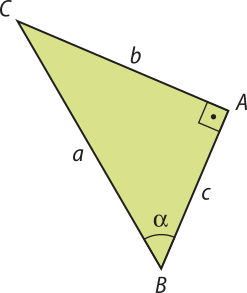
sen (alfa)" = e cos (alfa)" =
Dividindo sen (alfa)" por cos (alfa)", obtemos:
Assim, a 3ª relação está demonstrada.
ATIVIDADES RESOLVIDAS
1. Observe a representação de duas rampas com ângulos de inclinação diferentes. É possível determinar qual das duas rampas tem maior inclinação? Explique.


Resolução
Sim. pôdêmos determinar qual das duas rampas tem a maior inclinação calculando a razão entre a altura e o comprimento horizontal, quê é equivalente à tangente do ângulo de inclinação.
Sendo (alfa)" e (beta)" os ângulos de inclinação das rampas 1 e 2, respectivamente, temos:
Agora, comparamos as duas razões:
. Isso significa quê, para um mesmo comprimento horizontal (12 m), a rampa 1 corresponde a uma altura de 3 m, enquanto a rampa 2 corresponde a uma altura de 4 m.
Então, podemos concluir quê a rampa 2 tem maior inclinação do quê a 1.
2. Para medir a altura de uma torre, uma topógrafa se situa no ponto A, a 70 m da base da torre. Em seguida, com o teodolito, mira o ponto mais alto da torre e verifica quê o ângulo dessa linha visual com a horizontal (ângulo de observação) é de 32°, como indica a figura. Sabendo quê a distância do teodolito ao chão é desprezível, calcule a altura da torre.
Considere tg 32° = 0,625.
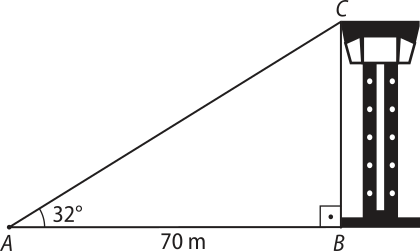
Resolução
Vamos representar a situação na figura a seguir, em quê AB é a distância da topógrafa até a base da torre e BC é a altura da torre.
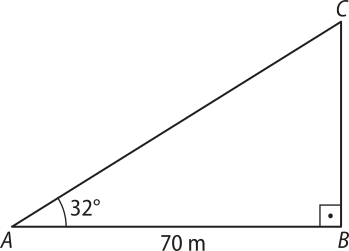
Para determinar a altura da torre, vamos usar o valor de tg 32°, dado no enunciado.
tg 32° = ⇒ 0,625 = ⇒ BC = 43,75
Portanto, a altura da torre é 43,75 m.
Página duzentos e oitenta e dois
3. Sabendo quê (alfa)" é um ângulo agudo de um triângulo retângulo ABC e quê cos (90° − (alfa)") = , calcule o valor da tg (alfa)".
Resolução
Como sen (alfa)" = cos (90° − (alfa)"), então: sen (alfa)" =
Pela relação fundamental, temos:
sen2 (alfa)" + cos2 (alfa)" = 1 ⇒ + cos2 (alfa)" = 1 ⇒
⇒ cos2 (alfa)" = 1 − ⇒ cos2 (alfa)" = ⇒
⇒ cos (alfa)" =
Como o ângulo (alfa)" é agudo, só o valor positivo nos interessa, pois definimos seno, cosseno e tangente como razões de medidas dos lados do triângulo. Assim, essas razões não podem sêr negativas. Usaremos esse fato ao longo de todo êste Capítulo.
Então:
Pela 3ª relação, obtemos:
tg (alfa)" = ⇒ tg (alfa)" = ⇒
⇒ tg (alfa)" = ⇒ tg (alfa)" =
⇒ tg (alfa)" =
4. ![]() Use uma calculadora científica para efetuar o quê é pedido nos itens.
Use uma calculadora científica para efetuar o quê é pedido nos itens.
a) Qual é o valor aproximado de sen 30°, de cos 30° e de tg 30°?
b) Determine o valor do ângulo (alfa)" para o qual sen (alfa)" ≃ 0,75.
Resolução
a) Inicialmente, é preciso indicar a unidade de medida de ângulo quê será usada, no caso, o grau. Para isso, na calculadora, escolha o modo D ou Deg – abreviaturas de degree, em inglês, quê significa "grau". Em seguida, pressione as teclas correspondentes para efetuar os cálculos.
• Para calcular o seno de 30°, devemos pressionar as teclas:

• Para calcular o cosseno de 30°, devemos pressionar as teclas:

• Para calcular a tangente de 30°, devemos pressionar as teclas:

Portanto, sen 30° = 0,5, cos 30° ≃ 0,866 e tg 30° ≃ 0,577.
b) Para determinar o valor do ângulo (alfa)", vamos usar a função ![]() da calculadora.
da calculadora.
Normalmente, ela fica na mesma tecla da função ![]() e é preciso usar a tecla
e é preciso usar a tecla ![]() para acioná-la. Assim, para obtêr o ângulo desejado, devemos pressionar as teclas:
para acioná-la. Assim, para obtêr o ângulo desejado, devemos pressionar as teclas:

Portanto, o ângulo cujo seno é aproximadamente 0,75 é 49°.
Saiba quê...
• Na maioria das calculadoras científicas, o seno de um ângulo é indicado por “sin”, e a tangente é indicada por "tan".
• A sequência de teclas póde variar dependendo do modelo da calculadora. Em alguns casos, digita-se primeiro o valor do ângulo e depois a razão desejada.
Para acessar
• NAKAMURA, Juliana. O quê é teodolito e como ele é usado na topografia? [Florianópolis]: Sienge, 15 jul. 2019. Disponível em: https://livro.pw/pufis. Acesso em: 7 ago. 2024.
Artigo quê traz informações detalhadas sobre o funcionamento do teodolito e suas limitações.
Página duzentos e oitenta e três
ATIVIDADES
1. Em cada caso, calcule o seno, o cosseno e a tangente do ângulo agudo destacado.
a)
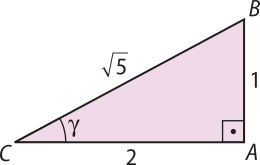
sen (gama)" =
cos (gama)" =
tg (gama)" =
b)
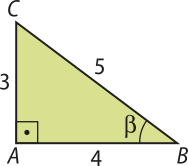
sen (beta)" =
cos (beta)" =
tg (beta)" =
2. Retomando a situação da construção da rampa da página 277, a NBR 9050 estabelece quê a inclinação deve sêr calculada de acôr-do com a expressão i = , em quê:
• i é a inclinação, em %;
• h é a altura do desnível;
• c é o comprimento da projeção ortogonal da rampa sobre o piso inferior.
Além díssu, para desníveis de até 0,80 m, a inclinação permitida deve estar entre 6,25% e 8,33%.
Com base nessas informações, responda.
a) A expressão da inclinação póde sêr relacionada com quê razão trigonométrica? Justifique.
Tangente. No triângulo retângulo formado, h é a medida do cateto ôpôsto ao ângulo de inclinação e c é a medida do cateto adjacente.
b) O quê significa uma inclinação de 8%?
Significa quê a razão entre a altura do desnível e o comprimento da projeção da rampa é de .
3. Quando os raios do sól formam o ângulo de 30° com o plano do chão, obtém-se a medida de 50 m para a sombra de um prédio. Qual é a altura aproximada dêêsse prédio? Adote tg 30° = 0,58.
29 m

4. Em um triângulo retângulo, um cateto méde 15 cm, e a hipotenusa, 17 cm. Calcule o seno, o cosseno e a tangente do maior ângulo agudo dêêsse triângulo.
sen (alfa)" = ;
cos (alfa)" = ;
tg (alfa)" =
5. Retomando a situação da introdução do Capítulo, determine a altura h do barranco, sabendo quê o teodolito está a 1,6 m do solo, alinhado com a base do barranco. Considere tg 41° = 0,87 e tg 50° = 1,19.
aproximadamente 66,31 m

6. Considere duas pessoas a 4 km de distância uma da outra, localizadas em dois pontos A e B no solo. A pessoa no ponto A, olhando na direção de B, avistou, segundo um ângulo de 50° (com a horizontal), um helicóptero. No mesmo instante, a pessoa no ponto B, olhando na direção de A, avistou o mesmo helicóptero segundo um ângulo de 45° (com a horizontal). Aproximadamente, a quê altura do solo o helicóptero estava naquele momento? Considere sen 45° = cos 45° e tg 50° ≃ 1,19.
aproximadamente 2,17 km ou 2.170 m
7. (Vunesp-SP) Um ciclista sobe, em linha reta, uma rampa com inclinação de 3 graus a uma velocidade constante de 4 metros por segundo.
A altura do topo da rampa em relação ao ponto de partida é de 30 m.

Use a aproximação sen 3° ≃ 0,05 e responda.
O tempo, em minutos, quê o ciclista levou para percorrer completamente a rampa é:
a) 2,5.
b) 7,5.
c) 10.
d) 15.
e) 30.
alternativa a
Página duzentos e oitenta e quatro
8. ![]() Determine a medida aproximada, em grau, do ângulo (alfa)" de cada figura. Utilize uma calculadora científica.
Determine a medida aproximada, em grau, do ângulo (alfa)" de cada figura. Utilize uma calculadora científica.
a)

(alfa)" ≃ 51°
b)

(alfa)" ≃ 19°
c)
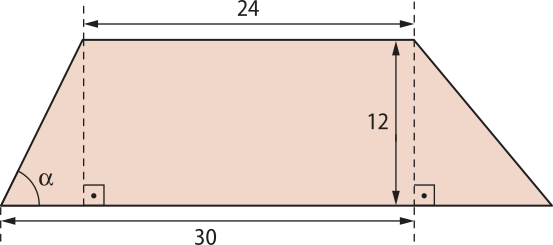
(alfa)" ≃ 63°
9. Considerando sen 10° = 0,17, sen 65° = 0,90 e cos 50° = 0,64, calcule:
a) cos 25°
0,90
b) cos 80°
0,17
c) sen 40°
0,64
10. (UEA-AM) A figura mostra os triângulos retângulos ABC e BCD, em quê AB = 12 cm e m(B D) = (alfa)".
alternativa a
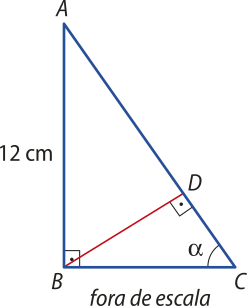
Sabendo quê sen (alfa)" = 0,8 e quê o ponto D está sobre o lado , a medida do segmento é igual a
a) 5,4 cm.
b) 3,6 cm.
c) 4,5 cm.
d) 6,3 cm.
e) 7,2 cm.
11. A soma dos comprimentos das bases de um trapézio retângulo vale 30 m. A base maior méde o dôbro da menor. Calcule a altura do trapézio, sabendo quê seu ângulo obtuso méde 150°. Considere sen 30° = 0,5.
m
12. (UECE) Um cabo de aço, medindo c metros de comprimento, é estendido em linha reta fixado em três pontos, a saber: P e Q em seus extremos e M em um ponto intermediário. O ponto P está localizado no solo plano horizontal e os pontos M e Q estão localizados nos altos de duas torres erguidas verticalmente no mesmo solo. As medidas, em metros, das alturas das torres e a distância entre elas são respectivamente h, H e d. Se x é a medida em graus do ângulo quê o cabo estendido faz com o solo, então, é correto dizêr quê a medida, em metros, da diferença entre a altura da torre maior e a altura da torre menor é igual a
alternativa b
a) c ⋅ tg (x).
b) d ⋅ tg (x).
c) tg (x).
d) tg (x).
13. Uma pessoa, distante 10 m de um prédio, observa o topo dele sôbi um ângulo de 58°. Ao afastar-se dêêsse prédio, ainda observa o topo, porém, agora, sôbi um ângulo de 22°. Calcule a altura do prédio e a distância de afastamento entre os pontos de observação. Adote tg 22° = 0,4 e tg 58° = 1,6.
O prédio tem 16 metros de altura, e a pessoa se afastou 30 metros.
14. Um submarino A, quê se encontra a uma profundidade de 400 m no mar, detecta dois barcos B e C na superfícíe da á gua sôbi ângulos de 62° e 40°, respectivamente, medidos entre a direção dos barcos e a direção perpendicular à superfícíe, como mostra a figura.
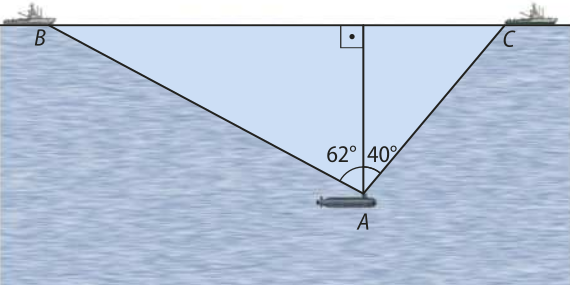
Qual é a distância aproximada entre os dois barcos? Adote tg 62° = 1,9 e tg 40° = 0,8.
1.080 m
15. Elabore um problema parecido com o da atividade 14, quê envolva uma pessoa localizada no solo observando dois drones situados no ar, à mesma altura do solo e a distâncias diferentes da pessoa. Depois, resôuva o problema e compartilhe com a turma.
Resposta pessoal.
Página duzentos e oitenta e cinco
FÓRUM
Estatuto da Criança e do Adolescente (ECA)
O Estatuto da Criança e do Adolescente (ECA), lei número 8.069, de 13 de julho de 1990, representa um marco legal na proteção e na promoção dos direitos fundamentais de crianças e adolescentes no Brasil, desde a gestação até a maioridade.
Um dos pontos do ECA é a perspectiva inclusiva, reconhecendo crianças e adolescentes como sujeitos de direitos, dotados de autonomia progressiva e em processo de desenvolvimento físico, mental, moral, espiritual e social. Isso implica quê as necessidades e os interesses dêêsses indivíduos devem sêr considerados em todas as esferas da vida social e jurídica.
Ao estabelecer direitos, como o acesso à educação de qualidade, a proteção contra o trabalho infantil e o direito à convivência familiar e comunitária, o ECA promove a construção de uma ssossiedade mais justa e equitativa. Garante-se, assim, quê crianças e adolescentes possam desenvolver todo o potencial quê possuem, contribuindo para o bem-estar coletivo e o desenvolvimento político, social e econômico do país.
Além díssu, o ECA estabelece medidas protetivas para situações de violência, abuso, negligência e exploração, garantindo quê crianças e adolescentes tênham mecanismos eficazes para buscar ajuda e proteção. Essas medidas incluem desde o acolhimento institucional até o fortalecimento dos vínculos familiares e comunitários.

BECK, Alexandre. [Por um mundo onde...]. Diário de Santa Maria, Santa Maria, 2019. Tirinha do Armandinho.
![]() Após ler o texto, discuta com os côlégas a questão a seguir.
Após ler o texto, discuta com os côlégas a questão a seguir.
• Vocês já conheciam o ECA? por quê é importante quê haja uma lei quê estabêlêça direitos específicos para esse grupo etário, em vez de simplesmente se aplicarem os mesmos direitos concedidos aos adultos?
Ver as Orientações para o professor.
Para ler
• TURMA da Mônica em: o Estatuto da Criança e do Adolescente. São Paulo: Instituto Mauricio de Sousa, 2021. Disponível em: https://livro.pw/vcrjn. Acesso em: 7 ago. 2024.
Revista em quadrinhos gratuita criada em parceria com o Ministério da Educação para difundir, com linguagem acessível, os principais aspectos do Estatuto da Criança e do Adolescente.

Página duzentos e oitenta e seis
Ângulos de 30°, de 45° e de 60°
As razões trigonométricas relacionadas aos ângulos de 30°, de 45° e de 60° podem sêr obtidas por meio de cálculos quê utilizam as medidas dos lados e dos ângulos de um triângulo equilátero e de um triângulo retângulo isósceles, como mostrado a seguir.
Saiba quê...
Em alguns textos, é possível quê você encontre a expressão "ângulos notáveis" para se referir aos ângulos de 30°, de 45° e de 60°.
Seno, cosseno e tangente dos ângulos de 30° e de 60°
Considere um triângulo equilátero ABC, no qual (éli)" é a medida dos lados e h é a medida da altura relativa ao lado , conforme mostra a figura.
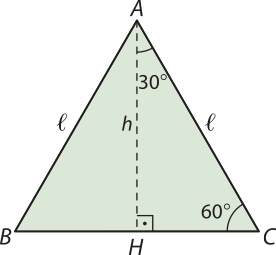
Como o triângulo ABC é equilátero, temos quê BH = HC = . Assim, no triângulo retângulo AHC, reto em H, aplicamos o teorema de Pitágoras para calcular a altura h:
(éli)"2 = h2 + ⇒ h = = =
E obtemos as seguintes razões:
• sen 30° =
• cos 30° =
• tg 30° =
• sen 60° =
• cos 60° =
• tg 60° =
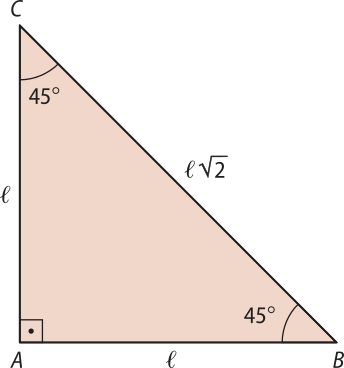
Seno, cosseno e tangente do ângulo de 45°
Considere um triângulo retângulo e isósceles ABC, conforme a figura a seguir, no qual (éli)" é a medida dos catetos e é a medida da hipotenusa, quê póde sêr determinada pelo teorema de Pitágoras.
Com base nesse triângulo ABC, obtemos as seguintes razões:
• sen 45° =
• cos 45° = _
• tg 45° = = 1
Página duzentos e oitenta e sete
pôdêmos organizar as razões trigonométricas dos ângulos de 30°, de 45° e de 60° em um qüadro, como o apresentado. Elas serão bastante utilizadas nas resoluções das atividades, evitando a necessidade de fazer cálculos com valores aproximados.
30° |
45° |
60° |
|
|---|---|---|---|
sen |
|||
cos |
|||
tg |
1 |
ATIVIDADES RESOLVIDAS
5. (UFV-MG) Um navio, navegando em linha reta, passa sucessivamente pêlos pontos A, B e C. O comandante, quando o navio está em A, observa um farol F e determina quê o ângulo F C méde 30°. Após navegar 6 km até o ponto B, ele verifica quê o ângulo F C méde 90°. Calcule a distância, em km, quê separa o farol F do navio quando êste se encontra no ponto C, situado a 2 km do ponto B.
Resolução
A figura representa a situação.
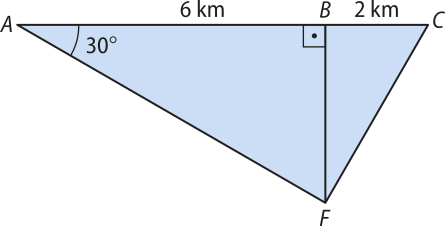
Do triângulo retângulo ABF, obtemos:
tg 30° = ⇒ ⇒ BF =
Logo, a distância BF é igual a _ km.
Aplicando o teorema de Pitágoras no triângulo BCF, temos:
(CF)2 = (BF)2 + (BC)2
(CF)2 = + 22
CF =
CF = 4, pois CF > 0.
Portanto, a distância entre o farol e o navio no ponto C é de 4 km.
6. Suponha quê um rio apresente um trecho de margens retas e paralelas, conforme mostra a figura.
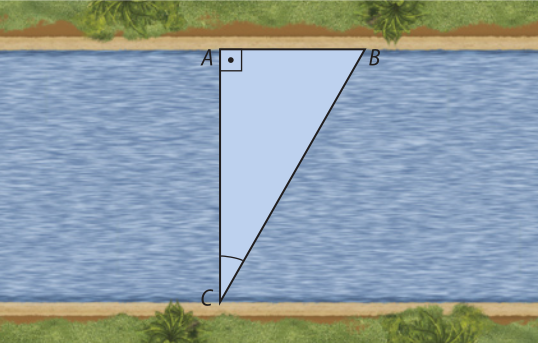
Os pontos A e B pertencem a uma das margens e C pertence à outra. Sabendo quê med(AC) = 60°, med(BC) = 90° e AB = 25 m, calcule a largura AC do rio.
Resolução
Considere o triângulo ABC, sêndo AC = x.
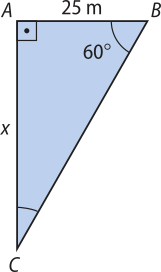
Temos:
tg 60° = ⇒ ⇒ x =
Portanto, a largura do rio é de m.
Página duzentos e oitenta e oito
ATIVIDADES
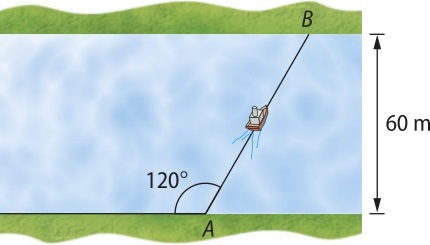
16. Um barco parte de A para atravessar um rio. A direção de seu deslocamento forma um ângulo de 120° com a margem do rio, conforme a figura. Sendo a largura do rio 60 m, qual é a distância AB percorrida pelo barco?
m
17. Uma escada, quê méde 2,20 m de comprimento, acha-se apoiada em uma parede vertical e forma um ângulo de 60° com o plano horizontal. Determine a quê altura o topo da escada se encontra do chão. Adote = 1,73.
1,903 m
18. Uma torre vertical de 12 metros de altura é vista sôbi um ângulo de 30° por uma pessoa quê se encontra a uma distância x do centro de sua base. O plano da base da torre está no nível dos olhos do observador. Determine a distância x. Adote tg 30° = 0,58.
x ≃ 20,7 m
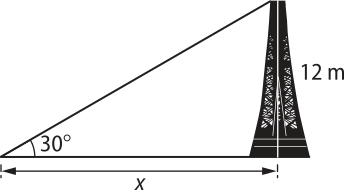
19. (UFG-GO) Para dar sustentação a um poste telefônico, utilizou-se um outro poste com 8 m de comprimento, fixado ao solo a 4 m de distância do poste telefônico, inclinado sôbi um ângulo de 60°, conforme a figura abaixo.
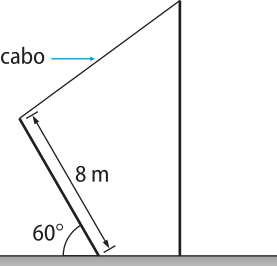
Considerando-se quê foram utilizados 10 m de cabo para ligar os dois póstes, determine a altura do poste telefônico em relação ao solo.
(6 + ) m
20. No triângulo ABC a seguir, é a altura relativa ao lado .
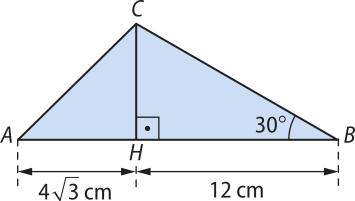
Determine:
a) a medida de . Adote tg 30° = ;
cm
b) a medida do ângulo B C.
45°
21. (IFSC) A ilustração a seguir representa a planta das ruas de uma cidade. A rua representada pelo segmento tem 50 m de comprimento. Um dos engenheiros do projeto de pavimentação dessas ruas esqueceu de indicar algumas distâncias. Considerando quê um de seus técnicos efetuou os cálculos, é CORRETO afirmar quê o total de metros da rua quê vai do ponto A até o ponto D é de:
alternativa e
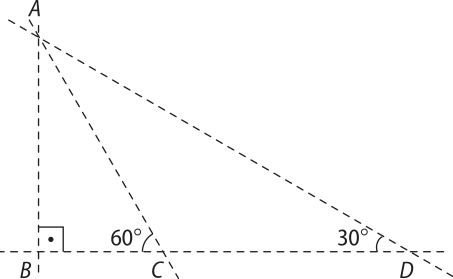
a) m.
b) m.
c) 50 m.
d) 100 m.
e) m.
22. (Fuvest-SP) No quadrilátero ABCD da figura abaixo, E é um ponto sobre o lado tal quê o ângulo A Eméde 60° e os ângulos E C e B D são rétos. Sabe-se ainda quê AB = cê dê = e BC = 1. Determine a medida de .
AD =
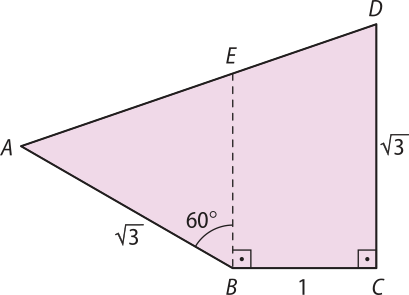
Página duzentos e oitenta e nove
23. (UFV-MG) Um passageiro em um avião avista duas cidades, A e B, sôbi ângulos de 15° e 30°, respectivamente, conforme a figura a seguir:
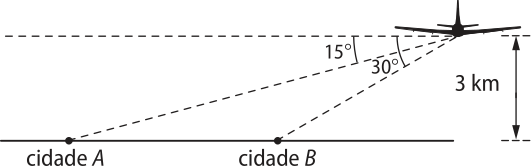
Se o avião está a uma altitude de 3 km, a distância entre as cidades A e B é:
a) 7 km.
b) 5,5 km.
c) 5 km.
d) 6,5 km.
e) 6 km.
alternativa e
24. A partir de um ponto, observa-se o topo de um prédio sôbi um ângulo de 30°. Caminhando 24 m em direção ao prédio, atinge-se outro ponto, de onde se vê o topo do prédio segundo um ângulo de 60°.
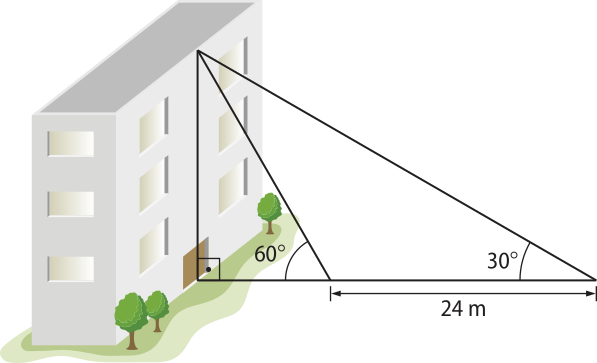
Desprezando a altura do observador, calcule, em métro, a altura do prédio.
m
25. (UECE) As medidas dos ângulos internos de um triângulo são respectivamente 30°, 60° e 90°. Se a medida do maior lado dêste triângulo é 4 cm, então, a medida, em cm, da altura relativa a êste lado é
alternativa c
a) .
b) .
c)
d)
26. (Unicamp-SP) Para medir a largura de um rio, um homem usou o seguinte procedimento: localizou um ponto B de onde podia vêr na margem oposta o coqueiro C, d fórma quê o ângulo A C fosse 60°; determinou o ponto D no prolongamento de , d fórma quê o ângulo C D fosse 90°. Medindo AD = 40 metros, achou a largura do rio. Determine essa largura e explique o raciocínio.
AC = 120m Ver as Orientações para o professor.
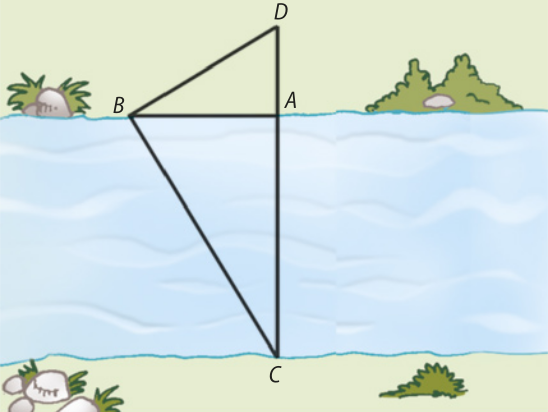
27. (UECE) José caminhou na praia em linha reta deslocando-se do ponto X ao ponto Y, perfazendo o total de 1.200 m. Quando estava no ponto X, vislumbrou um navio ancorado no ponto Z de tal modo quê o ângulo YXZ era de aproximadamente 60 graus. Ao chegar ao ponto Y verificou quê o ângulo XYZ era de 45 graus. Nessas condições, a distância do navio à praia, em metros, é aproximadamente igual a
alternativa b
a) 720.
b) 760.
c) 780.
d) 740.
Nota: Considere tg (60°) aproximadamente igual a .
28. ![]() Reúna-se a três côlégas para fazer a atividade de campo indicada a seguir.
Reúna-se a três côlégas para fazer a atividade de campo indicada a seguir.
Resposta pessoal.
• Primeiro, construam teodolitos caseiros seguindo a instrução disponível no vídeo https://livro.pw/vdvcb (acesso em: 7 ago. 2024).
• Em seguida, procurem, na escola ou no entorno dela, alturas ou distâncias de difícil medição diréta.
• Utilizem os teodolitos conforme as instruções do vídeo para obtêr as medidas necessárias.
• Por fim, façam os cálculos adequados para determinar as alturas escolhidas.
Página duzentos e noventa
EXPLORANDO A TECNOLOGIA
Razões trigonométricas usando o GeoGebra
Estudamos quê as razões trigonométricas em um triângulo retângulo não dependem da medida dos lados, e sim do ângulo em questão. Nesta seção, com o auxílio do GeoGebra, vamos comprovar esse fato com a construção de dois triângulos retângulos semelhantes. Para isso, siga a sequência de passos a seguir.
I. Para a construção, não vamos precisar da malha quadriculada nem dos eixos. Portanto, para ocultar esses elemêntos, na janela de visualização, clique em qualquer ponto com o botão direito do máuzi e, depois, tire a seleção de Exibir Eixos e de Exibir Malha para desabilitar os eixos e a malha quadriculada.
II. Com a ferramenta Semirreta, ![]() construa uma semirreta .
construa uma semirreta .
III. Usando a ferramenta Reta Perpendicular, ![]() construa uma reta perpendicular à semirreta quê passe pelo ponto B.
construa uma reta perpendicular à semirreta quê passe pelo ponto B.
IV. Na reta perpendicular, com a ferramenta Ponto, ![]() , construa um ponto C.
, construa um ponto C.
V. Usando novamente a ferramenta Semirreta, construa a semirreta .
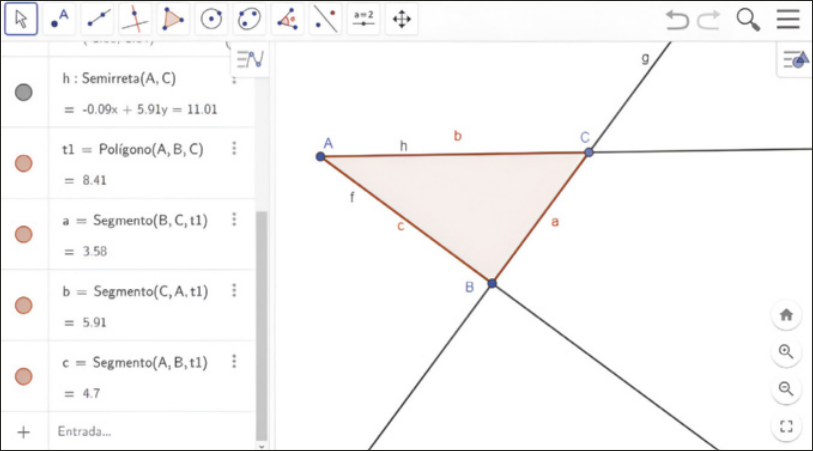
VI. Utilizando a ferramenta Polígono, ![]() clique sobre os pontos A, B, C e A, nessa ordem, para construir o triângulo ABC. A construção, até o momento, estará similar à imagem.
clique sobre os pontos A, B, C e A, nessa ordem, para construir o triângulo ABC. A construção, até o momento, estará similar à imagem.
VII. Agora, construa um ponto D, na semirreta , quê seja diferente de A e diferente de B. Esse ponto póde estar em qualquer lugar dessa semirreta.
VIII. Construa uma reta perpendicular a quê passe por D.
IX. Com a ferramenta Intersecção de Dois Objetos, ![]() construa o ponto E, clicando diretamente na intersecção entre a semirreta e a reta perpendicular construída.
construa o ponto E, clicando diretamente na intersecção entre a semirreta e a reta perpendicular construída.
X. Utilizando novamente a ferramenta Polígono, clique sobre os pontos A, D, E e A, nessa ordem, para construir o triângulo ADE.
Página duzentos e noventa e um
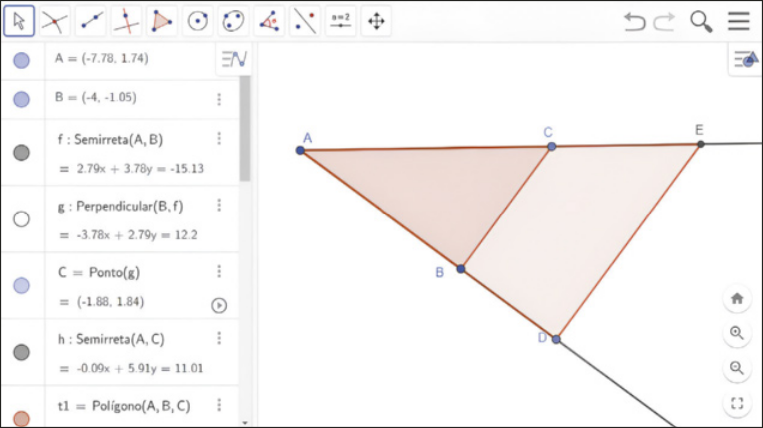
XI. Agora, vamos ocultar alguns itens da construção para facilitar a visualização.
Com a ferramenta Mover, ![]() selecione o elemento a sêr ocultado e clique sobre ele com o botão direito do máuzi para abrir a janela de opções; em seguida, tire a seleção de Exibir Objeto para esconder algum objeto da construção. Vamos ocultar as retas e .
selecione o elemento a sêr ocultado e clique sobre ele com o botão direito do máuzi para abrir a janela de opções; em seguida, tire a seleção de Exibir Objeto para esconder algum objeto da construção. Vamos ocultar as retas e .
Vamos ocultar, também, o nome de alguns elemêntos, mantendo apenas o nome dos pontos A, B, C, D e E. Para isso, basta selecionar cada objeto e, com o botão direito do máuzi, tirar a seleção de Exibir Rótulo.
A construção ficará similar a esta.
XII. No campo de entrada, digite “BC/AC”. Na janela de Álgebra, aparecerá o número indicado pela letra j, quê representa a razão j = . Em seguida, digite “AB/AC”, quê será representado pela letra k, e “BC/AB”, quê será representado pela letra l.
Digite, em seguida, “DE/AE”, “AD/AE” e “DE/AD”, quê serão representados, respectivamente, pelas lêtras m, n e o.
Observe, na imagem, como ficará a janela de Álgebra.
Note quê alguns dos números têm valores iguais.

Agora, faça o quê se pede nas atividades a seguir.
Ver as Orientações para o professor.
1. Os triângulos ABC e ADE construídos são semelhantes. Indique o caso de semelhança e justifique.
2. Ao observar a janela de Álgebra, percebemos quê j tem o mesmo valor de m, assim como os pares de números k e n, e l e o. O quê essas razões representam? O quê se póde concluir com essa informação?
3. Utilize a ferramenta Ângulo, ![]() e meça o ângulo com vértice em A. Em seguida, com a ferramenta Mover, altere a posição dos pontos A, B e D e dêz-creva o quê aconteceu com os valores do ângulo e das razões e o quê se póde concluir com essa informação.
e meça o ângulo com vértice em A. Em seguida, com a ferramenta Mover, altere a posição dos pontos A, B e D e dêz-creva o quê aconteceu com os valores do ângulo e das razões e o quê se póde concluir com essa informação.
4. Altere a posição do ponto C. A igualdade entre os pares de razões observada anteriormente se manteve?
Página duzentos e noventa e dois
CONEXÕES com...
LINGUAGENS E SUAS TECNOLOGIAS
A matemática do squêit
Altas manobras radicais, jovens atletas em ação e um estilo de vida. Estamos falando do squêit, quê entrou para o programa olímpico em Tóquio 2020. Mas a origem do esporte é na década de 1920, nos Estados Unidos, quando os jovens começaram a prender eixos e ró-dínhas em pedaços de madeira para se divertirem.
[…]
No final dos anos 50, quando não havia ondas no litoral da Califórnia, surfistas tentavam imitar as manobras quê faziam na á gua usando rodas e eixos fixados em pranchas de madeira.
No Brasil, o squêit chegou nos anos 60, primeiro no Rio de Janeiro, provavelmente trazido por filhos de norte-americanos e pêlos brasileiros quê viajavam para os Estados Unidos na época. Os skateboards evoluíram e atualmente são compostos por um deck de madeira, chamado de shape no Brasil, eixos de alumínio e as rodas de aderência para cada tipo de terreno. Para andar e consequentemente fazer as manobras é necessária uma combinação de impulso com os pés, equilíbrio e técnica.
O Brasil conta com nomes históricos da modalidade, bem antes da entrada nos Jogos Olímpicos, como Bób Burnquist, Sandro Dias, o Mineirinho, Letícia Buffoni, entre outros.
[…]
COMITÊ OLÍMPICO DO BRASIL. Skate: história. Rio de Janeiro: COB, c2024. Disponível em: https://livro.pw/fnjeq. Acesso em: 7 ago. 2024.
Saiba quê...
Na segunda edição do squêit nas Olimpíadas de Paris, em 2024, o Brasil conquistou duas medalhas de bronze: Rayssa Leal na categoria street e Augusto Akio na categoria park.

Página duzentos e noventa e três
Você já andou de squêit? Tem vontade? Você sabia quê, para construir uma rampa de squêit, podemos utilizar alguns conceitos de Trigonometria estudados neste Capítulo? Observe a fotografia.
Note quê a vista lateral de parte da rampa tem um formato semelhante ao de um triângulo retângulo. pôdêmos usar os conceitos de seno, cosseno e tangente para determinar as medidas da rampa de squêit.

Acompanhe a situação a seguir.
Qual é a altura de uma rampa de squêit, sabendo quê sua inclinação é de 30° e quê a placa de madeira quê sêrvirá de pista a ser colocada na parte inclinada tem o formato de um quadrado com lado de medida igual a 2 m? Observe a representação da lateral da rampa apresentada nesta situação.
Observe quê a medida H, quê queremos determinar, é a do cateto ôpôsto em relação ao ângulo de 30° e quê a medida 2 m é a da hipotenusa. Logo, utilizaremos o seno.
Como sen 30° = 0,5, temos:
sen 30° = ⇒ 0,5 = ⇒ H = 1
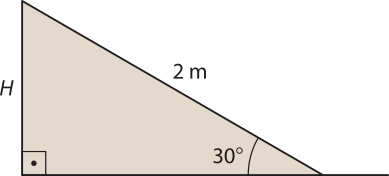
Assim, essa rampa tem 1 m de altura.
Agora, faça o quê se pede nas atividades a seguir.
1. ![]() O squêit se tornou esporte olímpico a partir dos Jogos Olímpicos de Tóquio 2020. Você conhece alguém quê pratíca esse esporte? Na sua cidade, há espaços para essa prática? Converse com os côlégas e com o professor a respeito díssu.
O squêit se tornou esporte olímpico a partir dos Jogos Olímpicos de Tóquio 2020. Você conhece alguém quê pratíca esse esporte? Na sua cidade, há espaços para essa prática? Converse com os côlégas e com o professor a respeito díssu.
Respostas pessoais.
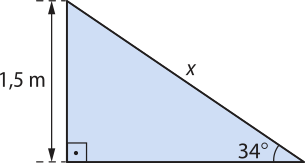
2. ![]() No squêit, há diversas modalidades e percursos. A minirrampa é utilizada por iniciantes para aprenderem as manobras. Normalmente, sua altura varia entre 1 métro e 2 metros e 40 centimetros. Considere a minirrampa representada e calcule a distância aproximada quê o iskeitista vai percorrer do topo da pista até a base.
No squêit, há diversas modalidades e percursos. A minirrampa é utilizada por iniciantes para aprenderem as manobras. Normalmente, sua altura varia entre 1 métro e 2 metros e 40 centimetros. Considere a minirrampa representada e calcule a distância aproximada quê o iskeitista vai percorrer do topo da pista até a base.
aproximadamente 2,68 m
3. ![]() Você já ouviu falar sobre squêit de dedos? Reúna-se em grupos, e pesquisem sobre essa modalidade. Depois, construam uma pista de squêit de dedos utilizando material reciclável e as noções de Trigonometria e apresentem-na para os outros grupos.
Você já ouviu falar sobre squêit de dedos? Reúna-se em grupos, e pesquisem sobre essa modalidade. Depois, construam uma pista de squêit de dedos utilizando material reciclável e as noções de Trigonometria e apresentem-na para os outros grupos.
Ver as Orientações para o professor.
Para assistir
• VIDA sobre rodas. Direção: Daniel Baccaro. São Paulo: Goma Filmes, 2010. Streaming (109 min).
Documentário quê conta a trajetória do squêit no Brasil nas dékâdâs de 1980 e 1990.
• MINDING The Gap. Direção: Bing Liu. Estados Unidos: ITVS/Kartemquin Films, 2018. Streaming (93 min).
Documentário quê narra a vida e as amizades de três jovens de Rockford (Illinois), Estados Unidos, unidos pelo amor ao squêit.
Página duzentos e noventa e quatro
ATIVIDADES COMPLEMENTARES
1. (UFAL) De um ponto A, situado no mesmo nível da base de uma torre, o ângulo de elevação do topo da torre é de 20°. De um ponto B, situado na mesma vertical de A e 5 m acima, o ângulo de elevação do topo da torre é de 18°. Qual a altura da torre? Dados: use as aproximações tg 20° ≃ 0,36 e tg 18° ≃ 0,32.
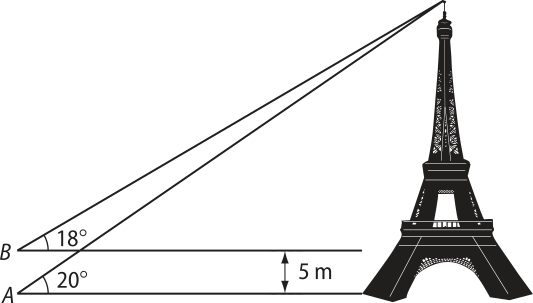
a) 42 m
b) 43 m
c) 44 m
d) 45 m
e) 46 m
alternativa d
2. (UFPel-RS) João viajou para o Rio de Janeiro e, como ele queria muito conhecer o Cristo Redentor, ficou horas admirando e tentando advinhar a altura da bela estátua.
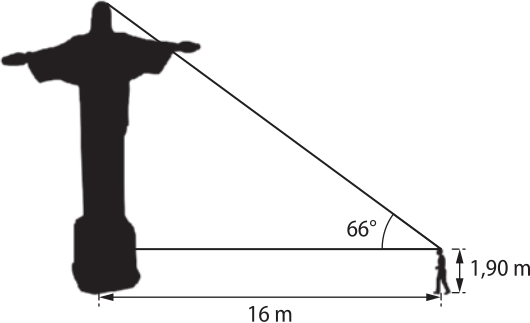
Considerando a figura e quê tg 66° ≃ 2,246, a altura aproximada do Cristo Redentor é de
a) 22 metros.
b) 48 metros.
c) 112 metros.
d) 55 metros.
e) 38 metros.
f) I.R.
alternativa e
Nota: nesse vestibular, o candidato tem pontos descontados caso escolha uma alternativa incorréta. Ao selecionar a alternativa I.R., quê indica “ignoro a resposta”, ele elimina essa possibilidade.
3. (Comvest) Na figura abaixo, o valor de sen (alfa)" é:
a)
b)
c)
d)
alternativa c
4. (hú éfe ême gê) A figura abaixo representa a travessia de um barco num rio de margens paralelas, cuja largura é de 150 m. O barco, saindo de A em direção ao ponto B, foi arrastado pela correnteza, indo em direção ao ponto C, segundo um ângulo de 60° com a margem.
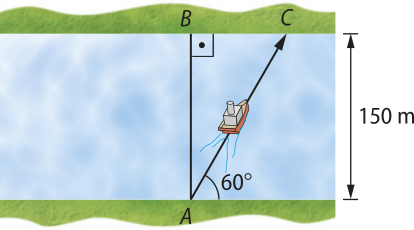
A distância, em metros, percorrida por esse barco foi de:
a) 75.
b) .
c) .
d) .
alternativa d
5. (IFSP) É comum encontrar em grandes supermercados esteiras rolantes para facilitar o deslocamento das pessoas. A figura a seguir mostra a esteira rolante de supermercado. Considerando os dados apresentados, o comprimento da parte da esteira rolante quê liga um andar ao outro é:
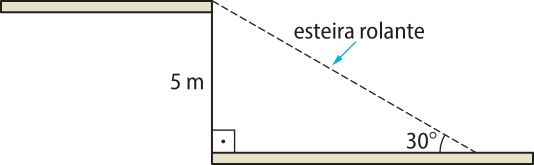
a) 5 m.
b) 10 m.
c) 15 m.
d) 20 m.
e) 25 m.
alternativa b
Página duzentos e noventa e cinco
6. (Enem/MEC) O mastro de uma bandeira foi instalado perpendicularmente ao solo em uma região plana. Devido aos fortes ventos, três cabos de aço, de mesmo comprimento, serão instalados para dar sustentação ao mastro. Cada cabo de aço ficará perfeitamente esticado, com uma extremidade num ponto P do mastro, a uma altura h do solo, e a outra extremidade, num ponto no chão, como mostra a figura.
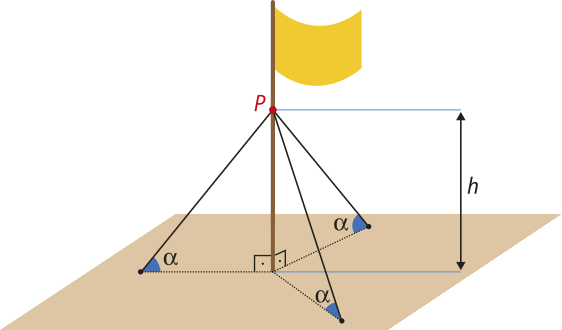
Os cabos de aço formam um ângulo (alfa)" com o plano do chão.
Por medida de segurança, há apenas três opções de instalação:
• opção I: h = 11 m e (alfa)" = 30°
• opção II: h = 12 m e (alfa)" = 45°
• opção III: h = 18 m e (alfa)" = 60°
A opção a sêr escolhida é aquela em quê a medida dos cabos seja a menor possível.
Qual será a medida, em métro, de cada um dos cabos a serem instalados?
alternativa c
a)
b)
c)
d)
e) 22
7. (Fuvest-SP) No cóódigo de Obras e Edificações da Prefeitura de São Paulo, encontra-se a regulamentação para vagas de estacionamento em um edifício para diferentes tipos de veículos. De acôr-do com o cóódigo, as dimensões de uma vaga de estacionamento são estabelecidas de acôr-do com o tipo de veículo, conforme a seguinte tabéla:
tabéla: Dimensões das vagas de estacionamento em função do tipo de veículo (medidas em metros).
Tipos de veículos |
Vagas para estacionamento |
|
|---|---|---|
Largura |
Comprimento |
|
Automóvel |
2,20 |
4,50 |
Carro para pessoa com deficiência |
3,70 |
5,50 |
Moto |
1,00 |
2,00 |
Utilitário |
2,50 |
5,50 |
Caminhão leve |
3,10 |
8,00 |
cóódigo de Obras e Edificações da Prefeitura de São Paulo. Adaptado.
Na figura a seguir, é apresentada parte de um projeto de garagem para um edifício. Foram projetadas vagas para automóveis e uma vaga para moto, no formato de paralelogramo, com ângulo (alfa)" de medida 60°.
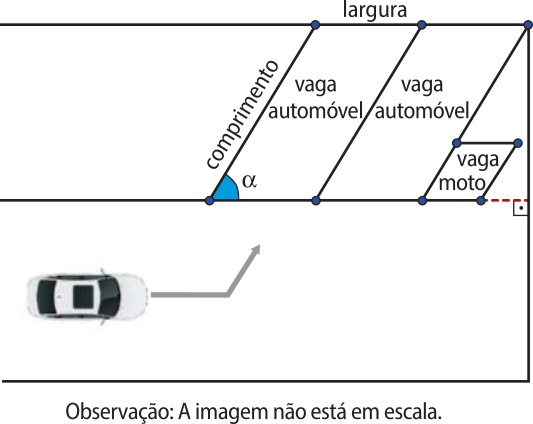
Após a vaga da moto, restou um espaço na garagem. Os responsáveis pela obra estão avaliando a possibilidade de colocar algum objeto quê possa sêr utilizado pêlos condôminos do edifício. Qual a medida do segmento destacado (tracejado) nesse espaço?
a) 0,75 m
b) 1,15 m
c) 1,25 m
d) 2,20 m
e) 2,25 m
alternativa c
Note e adote: cos (60°) = 0,5; sen (60°) =
Página duzentos e noventa e seis
8. (IFRS) Um drone se encontra a 100 m de altura no ponto A da figura abaixo, filmando um objeto quê se encontra no ponto B. O ângulo de rotação de sua câmera com o objeto é de 45°. A distância do drone até o objeto quê está sêndo filmado, em m, é:
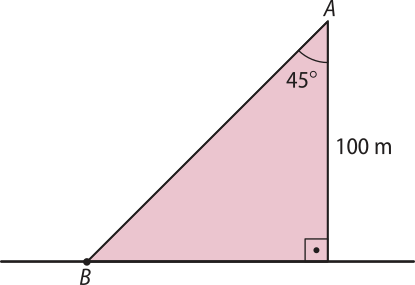
a) .
b) .
c) 145.
d) .
e) 200.
alternativa b
9. (UFV-MG) Um grupo de amigos rêzouvêo fazer uma viagem para um parque ecológico. Eles chegam à Estação Central e partem em um teleférico quê faz a primeira parada na Estação Minizoo, a segunda parada na Estação vista do Céu.
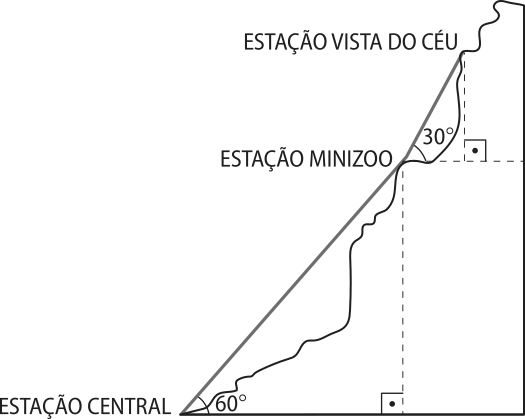
Suponha quê o comprimento total do cabo utilizado nesse teleférico seja de 480 metros, quê esse cabo permaneça sempre totalmente esticado e quê o comprimento dele da Estação Central à Estação Minizoo seja o triplo do comprimento do cabo da Estação Minizoo à Estação vista do Céu.
É CORRETO afirmar quê a altura da Estação vista do Céu em relação à Estação Central é:
(Adote = 1,7)
a) 364 metros.
b) 365 metros.
c) 366 metros.
d) 367 metros.
alternativa c
10. (UEA-AM) Um jardim, representado na figura pelo triângulo retângulo ABC, foi dividido em dois canteiros, S e S1, por uma grade, indicada pelo segmento .
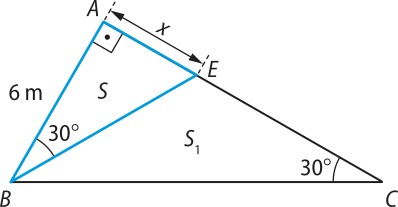
Sabendo quê AB = 6 m, o perímetro do triângulo ABE é igual a:
a) 4 + m.
b) m.
c) 6 + m.
d) m.
e) 6 + m.
alternativa c
11. (USCS-SP) Em um cartão quadrado ABCD, de área igual a 256 cm2, destaca-se uma região triangular ABP, conforme mostra a figura.
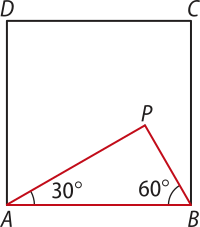
O perímetro da região delimitada pelo triângulo ABP é igual a:
a) 8(2 + )cm.
b) 6(3 + )cm.
c) cm.
d) 8(3 + )cm.
e) cm.
alternativa d
Página duzentos e noventa e sete
12. (Enem/MEC) Ao morrer, o pai de João, Pedro e José deixou como herança um terreno retangular de 3 km × 2 km quê contém uma área de extração de ouro delimitada por um quarto de círculo de raio 1 km a partir do canto inferior esquerdo da propriedade. Dado o maior valor da área de extração de ouro, os irmãos acordaram em repartir a propriedade de modo quê cada um ficasse com a terça parte da área de extração, conforme mostra a figura.
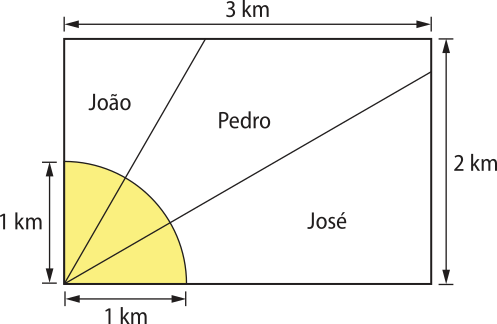
Em relação à partilha proposta, constata-se quê a porcentagem da área do terreno quê coube a João corresponde, aproximadamente, a:
a) 50%
b) 43%
c) 37%
d) 33%
e) 19%
alternativa e
PARA REFLETIR
Neste Capítulo, iniciamos o estudo da Trigonometria no triângulo. Utilizando o modelo matemático de uma rampa, analisamos a sua inclinação e as relações entre as suas medidas para conhecer as ideias de seno, cosseno e tangente, quê, em seguida, foram definidas matematicamente. Assim, exploramos os triângulos retângulos para determinar as relações entre as razões trigonométricas.
Nas páginas de abertura, conhecemos um pouco sobre a NBR 9050, norma quê regulamenta a construção de rampas para pessoas com mobilidade reduzida. Na Introdução, foi apresentado um problema de determinação da altura usando um teodolito mecânico. Depois de ter estudado o conteúdo dêste Capítulo, você consegue compreender como as relações trigonométricas auxiliam na medida de distâncias inacessíveis?
Vamos refletir a respeito das aprendizagens do Capítulo 8:
Respostas pessoais.
• Você já conhecia algum conceito de Trigonometria? Se sim, qual?
• Como você descreveria as razões trigonométricas em um triângulo retângulo?
• Dê exemplos de outras situações do dia a dia em quê é necessário determinar comprimentos (distâncias ou alturas) inacessíveis ou de difícil medição.
• O trabalho feito com o GeoGebra contribuiu para o seu entendimento das razões trigonométricas? Explique.
Página duzentos e noventa e oito
