Resoluções das atividades
Capítulo 1 • Conjuntos
Atividades
1. a) Como A é compôzto pêlos números naturais múltiplos de 3 e menóres do quê 20, então: A = {0, 3, 6, 9, 12, 15, 18}.
b) Como B é compôzto pêlos números naturais primos menóres do quê 27, então: B = {2, 3, 5, 7, 11, 13, 17, 19, 23}.
c) Como C é compôzto pêlos números naturais menóres do quê 50 e múltiplos de 7, então: C = {0, 7, 14, 21, 28, 35, 42, 49}.
d) O único satélite natural do planêta Terra é a Lua, então: D = {Lua}.
e) As consoantes da palavra “pedra” são p, d e r, então: E = {p, d, r}.
2.
a) Verdadeira, pois 1 é um elemento de B.
b) Falsa, pois {1} não é um elemento de B.
c) Verdadeira, pois 2 é um elemento de B.
d) Verdadeira, pois −1 é um elemento de B.
e) Falsa, pois 1 é um elemento de B.
f) Falsa, pois 3 não é um elemento de B.
• Respostas possíveis: b) 1 ∈ B; e) 4 ∉ B; f) 3 ∉ B
3.
a) O subconjunto de A formado por números maiores do quê 5 e menóres do quê 10 é {6, 7, 8, 9}.
b) O subconjunto de A formado por números pares é {4, 6, 8, 10}.
c) O subconjunto de A formado por números ímpares maiores do quê ou iguais a 7 é {7, 9, 11}.
4.
a) Todos os subconjuntos de E formados por 3 elemêntos são {2, 4, 6}; {2, 4, 8}; {2, 6, 8} e {4, 6, 8}.
b) O subconjunto de E formado por 4 elemêntos é {2, 4, 6, 8}.
5. Dois conjuntos são iguais quando possuem os mesmos elemêntos. Nesse caso, se {0, 1, 2} = {2, a, b}, em quê a e b são números naturais, tem-se: a = 0 e b = 1 ou a = 1 e b = 0. Assim, a + b = 1.
6.
a) Os subconjuntos quê podem sêr formados com duas músicas são {a, b}, {a, c}, {a, d}, {b, c}, {b, d} e {c, d}.
b) Formar todos os pares possíveis com as músicas a, b, c e d equivale a criar subconjuntos com dois elemêntos, ou seja, {a, b}, {a, c}, {a, d}, {b, c}, {b, d} e {c, d}. Portanto, o número de pares possíveis é 6.
7.
a) Verdadeira, pois todos os elemêntos do conjunto A também pertencem ao conjunto B; portanto, o conjunto A está contido em B.
b) Verdadeira, pois todos os elemêntos do conjunto C também pertencem ao conjunto B; portanto, o conjunto C está contido em B.
c) Falsa, pois alguns elemêntos do conjunto B não pertencem ao conjunto A; portanto, o conjunto B não está contido em A.
d) Falsa, pois não há elemêntos do conjunto A quê também pertençam ao conjunto C; portanto, o conjunto A não está contido em C.
e) Verdadeira, pois alguns elemêntos do conjunto B não pertencem ao conjunto A; portanto, o conjunto B não está contido em A.
f) Verdadeira, pois não há elemêntos do conjunto A quê também pertençam ao conjunto C; portanto, o conjunto A não está contido em C.
g) Verdadeira, pois todos os elemêntos do conjunto A também pertencem ao conjunto B; portanto, o conjunto A está contido em B. Consequentemente, o conjunto B contém o conjunto A.
h) Verdadeira, pois alguns dos elemêntos do conjunto B não pertencem ao conjunto A; portanto, o conjunto B não está contido em A. Consequentemente, o conjunto A não contém o conjunto B.
8.
a) Como o conjunto A é compôzto apenas pelo elemento 1, quê também pertence ao conjunto B, então pode-se afirmar quê A ⊂ B.
b) Como o conjunto A é compôzto apenas pelo elemento 1, quê também pertence ao conjunto C, então pode-se afirmar quê A ⊂ C.
c) Como o conjunto A é compôzto apenas pelo elemento 1, quê também pertence ao conjunto D, então pode-se afirmar quê A ⊂ D.
d) Como o elemento 0 pertence ao conjunto B, porém não pertence ao conjunto C, então pode-se afirmar quê B ⊄ C.
e) Como o conjunto B é compôzto pêlos elemêntos 0 e 1, e ambos pertencem ao conjunto D, então pode-se afirmar quê B ⊂ D.
f) Como o elemento 3 pertence ao conjunto C, porém não pertence ao conjunto D, então pode-se afirmar quê C ⊄ D.
9. Ao escrever os conjuntos na forma numérica, obtêm-se: A = {4, 6, 8, 10, 12, 14}, B = {0, 2, 4, 6, 8, 10, 12, 14} e C = {0, 4, 6, 8, 10, 12, 14,...}
a) Como todos os elemêntos do conjunto A também pertencem a B, então pode-se afirmar quê A ⊂ B.
b) Como todos os elemêntos do conjunto A também pertencem a C, então pode-se afirmar quê A ⊂ C.
c) Como o elemento 2 pertence ao conjunto B, mas não pertence a C, então pode-se afirmar quê B ⊄ C.
10. a) Verdadeira, pois 0 é um elemento de A.
b) Falsa, pois 1 é um elemento e não um subconjunto de A.
c) Verdadeira, pois 3 é um elemento de A.
d) Verdadeira, pois {3} é um subconjunto de A.
e) Falsa, pois 1 não é elemento de A. Consequentemente, {1, 2} não é subconjunto de A.
f) Verdadeira, pois o conjunto vazio é subconjunto de qualquer conjunto.
g) Falsa, pois o conjunto vazio não é um elemento de A.
h) Falsa, pois {3} não é um elemento de A.
11.
a) Verdadeira, pois o elemento 5 pertence aos dois conjuntos.
b) Verdadeira, pois os elemêntos a, b e c pertencem a ambos os conjuntos.
c) Falsa, pois o número 2 não está contido no conjunto {0, 2, 4}, o número 2 pertence ao conjunto {0, 2, 4}, ou seja, 2 ∈ {0, 2, 4}.
d) Verdadeira, pois o elemento 8 pertence ao conjunto {2, 4, 6, 8, 10}.
e) Verdadeira, pois os elemêntos 1 e 2 pertencem ao conjunto {1, 2, 3}.
f) Verdadeira, pois o conjunto dos números naturais não possui elemêntos negativos.
g) Verdadeira, pois o elemento 3 pertence ao conjunto {0, 3, 6, 9}.
Página trezentos e sessenta e um
h) Verdadeira, pois o número está localizado entre os números 0 e 1; portanto, não pertence ao conjunto dos números naturais. As afirmações verdadeiras são: a, b, d, e, f, g e h.
12. Como P ⊂ Q, pode-se admitir quê todos os elemêntos de P também pertencem a Q. A respeito de se Q ⊂ P, nada se póde afirmar. Porém, pode-se ter duas situações:
1. Caso essa afirmação seja verdadeira, deve-se considerar quê P = Q, ou seja, todos os elemêntos de Q também pertencem a P.
2. Caso essa afirmação seja falsa, então existe algum elemento de Q quê não pertence a P.
Com base nessas informações, pode-se julgar os itens:
a) Falsa, pois se x ∈ P e P está contido em Q, então x pertence a Q.
b) Falsa, pois ao considerar P = Q, então não existe elemento x ∈ Q e x ∉ P.
c) Falsa, pois ao considerar Q ⊄ P, então x póde pertencer a Q e não pertencer a P.
d) Verdadeira, se existir algum elemento quê não pertence a Q, então esse elemento também não pertence a P, pois P está contido em Q.
e) Falsa, pois, como P está contido em Q, os elemêntos de P também pertencem a Q; portanto, esses elemêntos de P são comuns a ambos os conjuntos. Resposta: alternativa d.
13. Como {1, 2} ⊂ M, M já possui os elemêntos 1 e 2. Agora, como M ⊂ {1, 2, 3, 4}, então as possibilidades são: M = {1, 2}, M = {1, 2, 3}, M = {1, 2, 4} ou M = {1, 2, 3, 4}. Portanto, 4 conjuntos.
14. Como A ⊂ B e B ⊂ C, pode-se concluir quê A ⊂ C, pois todos os elemêntos de A pertencem a B, quê, por sua vez, também pertencem a C.
Como todo elemento de C também pertence a A, pois C ⊂ A, então pode-se concluir quê A = C.
Portanto, como A ⊂ B e B ⊂ C e A = C, pode-se afirmar quê a relação entre os conjuntos é A = B = C, pois os elemêntos pertencentes a cada conjunto são comuns aos outros.
15. Pelo enunciado, sabe-se quê A = {0, 11, 12, 13, 14} e B = {11, 12}. Como o conjunto C é formado pêlos números pares compreendidos entre 11 e 19, obtém-se C = {12, 14, 16, 18}. Como o conjunto D é formado pêlos números ímpares compreendidos entre 10 e 16, obtém-se D = {11, 13, 15}.
Assim, ao utilizar as definições de união e intersecção entre conjuntos, obtêm-se:
a) A ⋂ B = {11, 12}
b) A ⋂ C = {12, 14}
c) B ⋃ C = {11, 12, 14, 16, 18}
d) C ⋃ D = {11, 12, 13, 14, 15, 16, 18}
e) Como A ⋃ B = {0, 11, 12, 13, 14} e C = {12, 14, 16, 18}; então (A ⋃ B) ⋃ C = {0, 11, 12, 13, 14} ⋃ {12, 14, 16, 18} = {0, 11, 12, 13, 14, 16, 18}.
f) Como A ⋂ C = {12, 14} e D = {11, 13, 15}; então (A ⋂ C) ⋂ D = {12, 14} ⋂ {11, 13, 15} = ∅.
16. Pelo enunciado, tem-se os conjuntos A = {m, n, p, q}; B = {n, p, q}; e C = {p, q, r, s}. Portanto:
a) A − B = {m, n, p, q} − {n, p, q} = {m}
b) A − C = {m, n, p, q} − {p, q, r, s} = {m, n}
c) B − C = {n, p, q} − {p, q, r, s} = {n}
d) A ⋂ B = {m, n, p, q} ⋂ {n, p, q} = {n, p, q} Como C = {p, q, r, s}; então (A ⋂ B) − C = {n, p, q} − {p, q, r, s} = {n}
e) Como A − C = {m, n} e B − C = {n}; então (A − C) ⋂ (B − C) = {m, n} ⋂ {n} = {n}
f) A − ∅ = {m, n, p, q} − ∅ = {m, n, p, q}
17. Ao observar o diagrama, pode-se escrever os seguintes conjuntos:
A = {1, 2, 3, 4, 9}, B = {2, 6, 7, 9} e C = {2, 4, 5, 6, 8}.
a) A ⋃ B = {1, 2, 3, 4, 9} ⋃ {2, 6, 7, 9} = {1, 2, 3, 4, 6, 7, 9}
b) A ⋃ C = {1, 2, 3, 4, 9} ⋃ {2, 4, 5, 6, 8} = {1, 2, 3, 4, 5, 6, 8, 9}
c) A ⋃ B ⋃ C = {1, 2, 3, 4, 6, 7, 9} ⋃ {2, 4, 5, 6, 8} = {1, 2, 3, 4, 5, 6, 7, 8, 9}
d) B ⋂ C = {2, 6, 7, 9} ⋂ {2, 4, 5, 6, 8} = {2, 6}
e) A ⋂ B = {1, 2, 3, 4, 9} ⋂ {2, 6, 7, 9} = {2, 9} Então, A ⋂ B ⋂ C = {2, 9} ⋂ {2, 4, 5, 6, 8} = {2}.
f) A − C = {1, 2, 3, 4, 9} − {2, 4, 5, 6, 8} = {1, 3, 9}
g) A ⋂ C = {1, 2, 3, 4, 9} ⋃ {2, 4, 5, 6, 8} = {2, 4} Então, (A ⋂ C) − B = {2, 4} − {2, 6, 7, 9} = {4}.
18. Ao se aplicar a definição de intersecção entre conjuntos, obtêm-se as respostas a seguir:
a) {10, 11, 12} ⋂ {7, 8, 9, 10, 11} = {10, 11}
b) {−3, −2, −1, 0} ⋂ {0, 1, 2, 3} = {0}
c) = ∅
19. O enunciado fornece as seguintes informações: A ⋃ B = {1, 2, 3, 4, 5, 6, 7}, A ⋂ B = {4, 5}, E − B = {1, 2}, B − A = {6, 7}, E ⋂ B = ∅ e E ⊂ A.
Considerando quê A ⋂ B = {4, 5} e B − A = {6, 7}, pode-se concluir quê B = {4, 5, 6, 7}, porque (A ⋂ B) ⋃ (B − A) = B. Agora, como A ⋃ B = {1, 2, 3, 4, 5, 6, 7}, A ⋂ B = {4, 5} e B = {4, 5, 6, 7}, pode-se concluir quê A = {1, 2, 3, 4, 5}.
Como E − B = {1, 2} e não existem elemêntos em comum entre eles, pois E ⋂ B = ∅, pode-se concluir quê E = {1, 2}. Com essas informações, pode-se construir o diagrama a seguir:
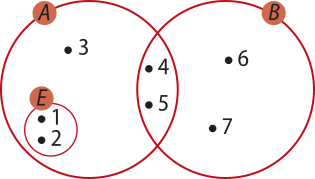
Assim, tem-se:
CAE = A − E = {1, 2, 3, 4, 5} − {1, 2} = {3, 4, 5}
20. Os conjuntos fornecidos pelo enunciado são: U = {0, 1, 2, 3, 4, 5, 6, 7}, A = {0, 2, 5}, B = {1, 3, 5, 7} e E = {2, 4, 6}.
a) CUA = U − A = {0, 1, 2, 3, 4, 5, 6, 7} − {0, 2, 5} = {1, 3, 4, 6, 7}
b) CUB = U − B = {0, 1, 2, 3, 4, 5, 6, 7} − {1, 3, 5, 7} = {0, 2, 4, 6}
c) CUE = U − E = {0, 1, 2, 3, 4, 5, 6, 7} − {2, 4, 6} = {0, 1, 3, 5, 7}
21. Conforme o enunciado, deve-se considerar M(a) o conjunto dos múltiplos de a e D(a) o conjunto dos divisores de a.
a) M(3) = {0, 3, 6, 9, 12, 15, 18, 21, 24, 27, 30, 33,...} e D(30) = {1, 2, 3, 5, 6, 10, 15, 30}
Então, M(3) ⋂ D(30) = {3, 6, 15, 30}.
b) M(2) = {0, 2, 4, 6, 8, 10,...} e M(4) = {0, 4, 8, 12, 16,...}
Então, M(2) ⋂ M(4) = {0, 4, 8,...}.
c) D(100) = {1, 2, 4, 5, 10, 20, 25, 50, 100} e D(50) = {1, 2, 5, 10, 25, 50}
Então, D(100) ⋂ D(50) = {1, 2, 5, 10, 25, 50}.
d) M(7) = {0, 7, 14, 21, 28, 35, 42, 49, 56,...} e M(5) = {0, 5, 10, 15, 20, 25, 30, 35, 40,...}
Então, M(7) ⋂ M(5) = {0, 35, 70,...}.
Página trezentos e sessenta e dois
22. Considere x o número de elemêntos do conjunto B; então, de acôr-do com o enunciado, temos:
n(B) = x
n(A) = x + 15
n(A ⋂ B) = 134
n(A ⋃ B) = 49
Como n(A ⋂ B) = n(A) + n(B) − n(A ⋃ B), ao substituir os valores, obtemos:
134 = x + 15 + x − 49
134 − 15 + 49 = 2x
2x = 168 ⇒ x = 84
Então, n(A) = 84 + 15 ⇒ n(A) = 99.
Portanto, o número de elemêntos de A é 99.
23. Considerando U o conjunto universo, A o conjunto das pessoas quê liam o jornál A e B o conjunto das pessoas quê liam o jornál B, de acôr-do com o enunciado, pode-se construir o diagrama a seguir:
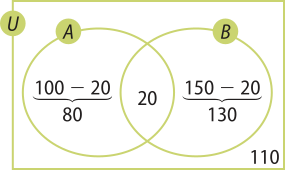
Portanto, considerando cada situação do diagrama, pode-se afirmar quê o número de pessoas consultadas foi: 80 + 20 + 130 + 110 = 340
Portanto, 340 pessoas.
24. Considerando U o conjunto universo, I o conjunto dos estudantes quê cursam Inglês e E o conjunto dos quê cursam Espanhol, de acôr-do com o enunciado, pode-se construir o diagrama a seguir:
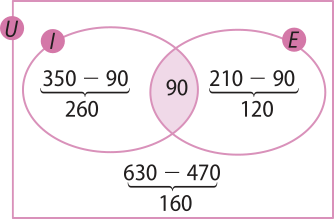
Pelo diagrama, tem-se:
a) Se 350 estudantes cursam Inglês e 90 deles também cursam Espanhol, então o número de estudantes quê cursam apenas Inglês é:
350 − 90 = 260.
Portanto, 260 estudantes cursam apenas Inglês.
b) Se 210 estudantes cursam Espanhol e 90 deles cursam Inglês e Espanhol, então o número de estudantes quê cursam apenas Espanhol é:
210 − 90 = 120.
Portanto, 120 estudantes cursam apenas Espanhol.
c) Se 260 estudantes cursam apenas Inglês, 120 apenas Espanhol e 90 cursam esses dois idiomas, então o número de estudantes quê cursam Inglês ou Espanhol é:
260 + 90 + 120 = 470.
Portanto, 470 estudantes cursam Inglês ou EspanhoI.
d) Se a escola tem 630 estudantes, dos quais 470 cursam Inglês ou Espanhol, o número de estudantes quê não cursam nenhum dos dois idiomas é: 630 − 470 = 160.
Portanto, 160 estudantes não cursam nenhum dos dois idiomas.
25. Sejam X o conjunto dos esportistas quê jogam xadrez, V dos quê jogam vôlei e T dos quê jogam tênis. Pode-se criar um diagrama começando pelo valor da intersecção dos três conjuntos e, em seguida, adequando o diagrama conforme as informações do enunciado. Observar a seguir o diagrama:
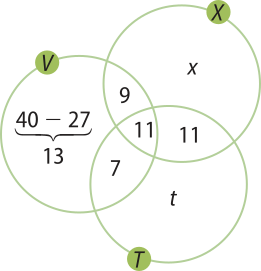
a) Sejam x o número de pessoas quê jogam apenas xadrez e t o número de pessoas quê jogam apenas tênis. Do enunciado, temos: x + 9 + 11 + 11 = t + 7 + 11 + 11 x + 9 =
= t + 7, portanto t = x + 2. Como o total de esportistas é 99, temos:
40 + x + 11 + t = 99
40 + x + 11 + x + 2 = 99
2x + 53 = 99
2x = 46, portanto x = 23 e t = 25.
São 25 pessoas quê jogam apenas tênis e 11 pessoas quê jogam tênis e xadrez, mas não jogam vôlei. Logo:
25 + 11 = 36
36 esportistas jogam tênis, mas não jogam vôlei.
b) São 25 pessoas quê jogam apenas tênis, 23 quê jogam apenas xadrez e 11 quê jogam xadrez e tênis, mas não jogam vôlei. Logo:
25 + 23 + 11 = 59
59 esportistas jogam xadrez ou tênis, mas não jogam vôlei.
c) São 13 pessoas quê jogam apenas vôlei e 7 pessoas quê jogam vôlei e tênis, mas não jogam xadrez. Logo:
13 + 7 = 20
20 esportistas jogam vôlei e não jogam xadrez.
26. a) Como os elemêntos do conjunto A são números naturais menóres do quê 8, então: A = {0, 1, 2, 3, 4, 5, 6, 7}
b) Como os elemêntos do conjunto C são números inteiros não nulos menóres do quê 4 e maiores do quê −3, então:
C = {−2, −1, 1, 2, 3}
27. Exemplo de resposta:
a) M = {x ∈ ℕ | 6 ≤ x ≤ 8}
b) T = {x ∈ ℤ | x ≤ −1}
28. Segundo o enunciado, o conjunto A é definido por A = {0, 2, 4, 6, 8} e B = {1, 3, 5, 7}. Logo:
a) 4 ∈ A
c) 8 ∈ A
e) 1 ∈ B
b) 5 ∉ A
d) 2 ∉ B
f) 10 ∉ A
29. a) Considerando quê k é um número natural e quê a lei é x = 2k, tem-se:
k = 0 ⇒ x = 0
k = 2 ⇒ x = 4
k = 1 ⇒ x = 2
Portanto, o conjunto é A = {0, 2, 4,...}.
b) Considerando quê k é um número natural e quê a lei é x = k2, tem-se:
k = 0 ⇒ x = 0
k = 2 ⇒ x = 4
k = 1 ⇒ x = 1
k = 3 ⇒ x = 9
Portanto, o conjunto é B = {0, 1, 4, 9,...}.
30. Segundo o enunciado, os conjuntos A e B são definidos por:
A = {2, 4, 6, 8, 10, 12,...} e B = {0, 1, 2, 3, 4, 5, 6, 7, 8, 9, 10}. Logo:
A ⋃ B = {2, 4, 6, 8, 10}
Portanto, n(A ⋃ B) = 5.
Página trezentos e sessenta e três
31. Segundo o enunciado, o conjunto A é definido por A = {2, 3}. Já o conjunto B é definido pelas raízes da equação produto (x − 2)(x − 3) = 0. Pela equação, temos x − 2 = 0 ou x − 3 = 0. Logo, x = 2 ou x = 3. Portanto, B = {2, 3}.
32. De acôr-do com as definições de número natural, número inteiro e número racional, pode-se afirmar quê:
a) −7 ∉ ℕ, pois os números naturais assumem somente valores positivos.
b) 4 ∈ ℤ, pois 4 é um número natural e, consequentemente, também é inteiro.
c) ∉ ℤ, pois é uma fração e não um número inteiro.
d) 0,166... ∈ ℚ, pois 0,166... é uma dízima periódica cujo período é 6.
33. a) Fazendo x = 0,323232... e multiplicando ambos os membros por 100, obtém-se: 100x = 32,323232...
Subtraindo, membro a membro, as duas igualdades, temos:
100x − x = 32,323232... − 0,323232...
99x = 32 ⇒ x =
b) Fazendo z = 2,715715... e multiplicando ambos os membros por 1.000, obtém-se:
1.000z = 2.715,715715...
Subtraindo, membro a membro, as duas igualdades, temos:
1.000z − z = 2.715,715715... −2,715715...
999z = 2.713 ⇒ z =
34. Considerando o enunciado, os conjuntos A e B são:
a) Divisores de 18: A = {1, 2, 3, 6, 9, 18}
b) Divisores de 30: B = {1, 2, 3, 5, 6, 10, 15, 30}
c) Divisores comuns de 18 e 30: C = A ⋂ B ⇒ C = {1, 2, 3, 6}
d) O mássimo divisor comum entre 18 e 30 é 6.
35. Considerando o enunciado, os conjuntos A, B e C são: A = {0, 2, 4, 6, 8, 10, 12,...}, B = {0, 3, 6, 9, 12, 15, 18,...} e C = {0, 5, 10, 15,...}
Portanto:
A ⋃ C = {0, 2, 4, 5, 6, 8, 10, 12, 14, 15, 16, 18, 20,...}
B − (A ⋃ C) = {0, 3, 6, 9, 12, 15, 18,...} − {0, 2, 4, 5, 6, 8, 10, 12, 14, 15, 16, 18, 20,...} = {3, 9, 21, 27, 33, 39, 51, 57, 63, 69,...}
Pode-se observar quê o conjunto B − (A ⋃ C) é compôzto por números múltiplos de 3 quê não são pares nem múltiplos de 5. Como, pelo enunciado, são solicitados os 10 primeiros números, tem-se: 3, 9, 21, 27, 33, 39, 51, 57, 63, 69
36. Por tentativa e êrro, temos:
15² + 16² = 225 + 256 = 481.
37. a) −2x − 9x + 5 = 0
11x = 5 ⇒ x =
Portanto, M = .
b) + a = 2 ⇒ a =
Portanto, N = .
c) Como (y − 1)(y + 2)(y − 3) = 0 é uma equação produto, então y − 1 = 0 ou y + 2 = 0 ou y − 3 = 0.
Logo, y = 1 ou y = −2 ou y = 3.
Portanto, P = {−2, 1, 3}.
d) Resolvendo a equação x2 − 25 = 0 ⇒ (x + 5)(x − 5) = 0
Então, x + 5 = 0 ou x − 5 = 0.
Logo, x = −5 ou x = 5.
Como x é natural, então S = {5}.
38. Primeiro, vamos obtêr 7,363636... na forma de fração.
a = 7,363636...
100a = 736,363636...
100a − a = 736,363636... − 7,363636...
99a = 729
a = =
Então, a razão póde sêr representada por ou por qualquer fração equivalente:
Se x = 162 e y = 22, então x dividido por y tem quociente 7 e résto 8, o quê respeita as condições do enunciado.
Portanto, x = 162, y = 22 e z = 7. Assim:
x + y + z = 162 + 22 + 8 = 192
Resposta: alternativa d.
39. Observando a ilustração, pode-se considerar quê o número x é aproximadamente 1,6. Logo:
2x − 2 = 2 ⋅ 1,6 − 2 = 3,2 − 2 = 1,2 ≃ U.
Resposta: alternativa d.
40. Obtendo a fração geratriz da dízima 0,333..., tem-se:
x = 0,333...
10x = 3,333...
Subtraindo, membro a membro, as duas igualdades:
10x − x = 3,333... − 0,333...
9x = 3 ⇒ x =
Portanto:
= 18
Resposta: alternativa c.
41. Para ordenar números racionais, pode-se encontrar uma fração equivalente, para cada um deles, com um mesmo denominador. Como o mmc(24, 3, 8) = 24, pode-se reescrever os números p = , q = e r = como frações equivalentes de mesmo denominador, no caso, 24.
Portanto, obtêm-se: p = , q = e r =
Logo, p < r < q.
Resposta: alternativa a.
42. a) 3x − 4x − 4 = 0 ⇒ x = −4
Como x é natural, então A = ∅.
b) x2 − 7 = 0 ⇒ (x + _ )(x − _) = 0
Então, x + _ = 0 ou x − = 0.
Logo, x = − ou x = .
Portanto, B = .
c) + 0,25a + a = 2
2a = 2 ⇒ a = 1
Portanto, C = {1}.
d) 3 + x2 = 4 ⇒ x2 − 1 = 0 ⇒
⇒ (x + 1)(x − 1) = 0
Então, x + 1 = 0 ou x − 1 = 0.
Logo, x = −1 ou x = 1.
Portanto, D = {−1, 1}.
Página trezentos e sessenta e quatro
e) + y = ⇒ 4y = ⇒ y =
Portanto, E = .
f) x2 − 4 = 0 ⇒ (x + 2)(x − 2) = 0
Então, x + 2 = 0 ou x − 2 = 0.
Logo, x = −2 ou x = 2.
Portanto, F = {−2, 2}.
43. Em cada item, deve-se substituir √ 3 pela aproximação 1,732.
a)
O valor da expressão é aproximadamente 1,866.
b)
O valor da expressão é aproximadamente 0,616
44. Exemplo de resposta:
a) Como todo número irracional possui inverso, ao calcular o produto entre um irracional e seu respectivo inverso, obtém-se 1 como resultado. Como exemplo, pode-se considerar a = _ e b = , assim a ⋅ b = 1, quê não é um número irracional.
b) Como todo número irracional possui ôpôsto, ao calcular a soma entre um irracional e seu respectivo ôpôsto, obtém-se 0 como resultado. Como exemplo, pode-se considerar a = e b= , assim a + b = 0, quê não é um número irracional.
45. Ao desenvolver o produto ( + 1)( − 1), obtém-se
− 12 = 3 − 1 = 2, ou seja, é um número racional.
Agora, ao representar a dízima periódica 0,999... na forma de fração, tem-se:
x = 0,999...
10x = 9,999...
Subtraindo, membro a membro, as duas igualdades, temos:
10x − x = 9,999... − 0,999...
9x = 9 ⇒ x = ⇒ x = 1
Portanto, 0,999... é um número racional.
Assim, deve-se considerar quê ambos os números são racionais.
Resposta: alternativa b.
46.
a) Como se deve considerar todos os números entre 6 e 10, inclusive ambos, a notação de conjunto ficará {x ∈ ℝ | 6 ≤ x ≤ 10}.
b) Como se deve considerar todos os números entre −1 e 5, desconsiderando o −1 e incluindo o 5, a notação de conjunto ficará {x ∈ ℝ | −1 < x ≤ 5}.
c) Como se deve considerar todos os números entre −6 e 0, sêndo ambos desconsiderados, a notação de conjunto ficará {x ∈ ℝ | −6 < x < 0}.
d) Como se deve considerar todos os números maiores do quê 0, incluindo o próprio 0, a notação de conjunto ficará {x ∈ ℝ | x ≥ 0}.
e) Como se deve considerar todos os números menóres do quê 3, a notação de conjunto ficará {x ∈ ℝ | x < 3}.
47. Deve-se representar os intervalos na reta real, observando os extremos de cada intervalo.
a) Todos os números entre 2 e 8, sêndo ambos considerados.

b) Todos os números menóres do quê 2, considerando o número 2.

c) Todos os números entre −6 e −1, considerando o número
−6 e não considerando o −1.

d) Todos os números maiores do quê 2, considerando o número 2.

e) Todos os números entre 2 e 5, sêndo ambos desconsiderados.

f) Todos os números entre −2 e 2, sêndo ambos considerados.

48. Nesta atividade, deve-se observar a reta real, principalmente os extremos, e verificar se esses pertencem, ou não, ao intervalo.
a) O intervalo representa os números compreendidos entre os extremos 2 e 4. Como as bó-linhas estão cheias, ambos devem sêr considerados. Portanto, o conjunto é {x ∈ ℝ | 2 ≤ x ≤ 4}.
b) O intervalo representa os números maiores do quê 1. Como a bó-linha está vazia, devemos desconsiderar esse extremo. Portanto, o conjunto é {x ∈ ℝ | x > 1}.
c) O intervalo representa os números compreendidos entre os extremos _ e 5. Como as bó-linhas estão vazias, ambos devem sêr desconsiderados. Portanto, o conjunto é _ .
d) O intervalo representa os números menóres do quê . Como a bó-linha está cheia, devemos considerar esse extremo. Portanto, o conjunto é .
49. a) Considerando quê o conjunto A é o intervalo aberto entre 0 e 3 e quê o conjunto B é o intervalo aberto entre 1 e 5, a união entre eles será:
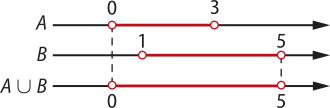
A ∪ B = {x ∈ ℝ | 0 < x < 5}
b) Considerando quê o conjunto A é o intervalo aberto em −4
e fechado em 1 e quê o conjunto B é o intervalo fechado entre 2 e 3, a união entre eles será:

A ∪ B = {x ∈ ℝ | −4 < x ≤ 1 ou 2 ≤ x ≤ 3}
c) Considerando quê o conjunto A é o intervalo aberto entre 2
e 5 e quê o conjunto B é o intervalo aberto entre 1 e 4, a união entre eles será:
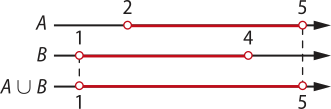
A ⋃ B = {x ∈ ℝ | 1 < x < 5}
Página trezentos e sessenta e cinco
d) Considerando quê o conjunto A é o intervalo fechado em −2 e aberto em 2 e quê o conjunto B é o intervalo aberto com os números maiores do quê 0, a união entre eles será:
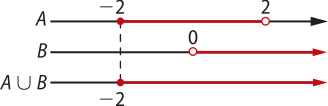
A ⋃ B = {x ∈ ℝ | x ≥ −2}
50. Pelo enunciado, pode-se considerar quê os conjuntos são representados da seguinte forma:
Conjunto A: intervalo fechado em −1 e aberto em 6;
conjunto B: intervalo aberto em −4 e fechado em 2;
conjunto E: intervalo aberto em −2 e 4.
a) (B ⋃ E) − A
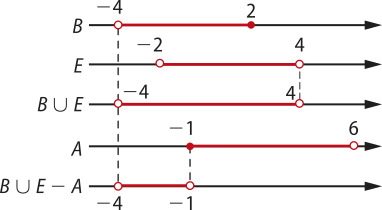
(B ⋃ E) − A =]−4, −1[
b) E − (A ⋂ B)

E − (A ⋂ B) =]−2, −1[ ⋃] 2, 4[
51. Como ambos os números x e y são números decimais e estão entre 0 e 1, o produto de x por y está entre 0 e x, pois será um número estritamente menor do quê x. Resposta: alternativa b.
Atividades complementares
1. Segundo o enunciado, como A ⋂ B = {f, g}, B ⋂ C = {b, f} e C ⋂ A = {e, f}, pode-se concluir quê A ⋂ B ⋂ C = {f}. Com base nisso e considerando as informações do enunciado, pode-se construir o diagrama a seguir:
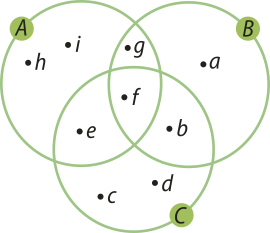
Assim, pode-se escrever os conjuntos:
A = {e, f, g, h, i}, B = {a, b, g, f} e C = {b, c, d, e, f}.
Resposta: alternativa c.
2. Segundo o enunciado, 10 alunos acertaram ambas as kestões, 25 alunos acertaram a primeira questão e 20 alunos acertaram a segunda questão. Assim, pode-se construir o seguinte diagrama:
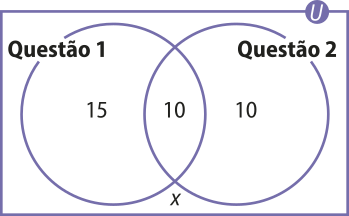
Como a sala de aula possui 40 alunos, tem-se:
15 + 10 + 10 + x = 40
Ao resolver a equação, obtém-se x = 5.
Resposta: alternativa e.
3. Considerando x o número de pessoas com tipo sangüíneo AB, de acôr-do com o enunciado, podemos montar o seguinte diagrama:
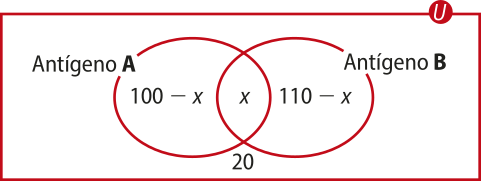
Como foram coletadas amostras de sangue de 200 pessoas, tem-se:
200 = 100 − x + x + 110 − x + 20
200 = 230 − x
x = 230 − 200 ⇒ x = 30
Assim, o número de pessoas com tipo sangüíneo A é:
100 − x = 100 − 30 = 70
Portanto, 70 pessoas.
Resposta: alternativa c.
4. Sabe-se, pelo enunciado, quê três candidatos concorreram a uma eleição e quê os eleitores votaram em apenas dois candidatos. Assim, ao construir um diagrama representando essa situação, deve-se considerar quê a intersecção entre os três conjuntos, A, B e C, deve sêr representada por 0. Além díssu, também deve-se considerar nulos os espaços reservados para apenas um candidato, pois ninguém votou apenas em uma pessoa. Ver a seguir esse diagrama:

Assim, pode-se concluir quê o candidato A recebeu 120 votos, o candidato B recebeu 180 votos e o candidato C recebeu 100 votos.
Portanto, o candidato B venceu com 180 votos.
Resposta: alternativa e.
Página trezentos e sessenta e seis
5.
Resposta: alternativa a
6. Como = −3,4, conclui-se quê:
−4 < < −3.
Portanto, o número foi marcado entre −4 e −3.
Resposta: alternativa d.
7. Para definir o intervalo em quê o número (pi)" − está localizado, pode-se obtêr valores aproximados, na forma decimal, para (pi)" e para _ Assim, (pi)" ≃ 3,14 e _ ≃ 1,41. Logo, 3,14 − 1,41 = 1,73.
Portanto, (pi)" − _ está localizado entre e 2.
Então, o valor (pi)" − está no intervalo .
Resposta: alternativa c.
8. I. Verdadeira, pois a e b são reais positivos, então:
a > b ⇒ > 1 ⇒ > ⇒ >
II. Falsa, pois, para a = 4 e b = 9, temos: + = 2 + 3 = 5
III. Falsa, pois, para a = e b = , temos: + = + =
Logo, apenas a afirmação I está correta.
Resposta: alternativa a.
9. Para calcular a diferença A − B, deve-se representar os conjuntos A e B na reta numérica e, em seguida, construir um diagrama. Portanto, reescrevendo os conjuntos A e B na forma de intervalos, obtêm-se: A = [−4, 3] e B = [−2, 5[.
Representando-os no diagrama, obtém-se:
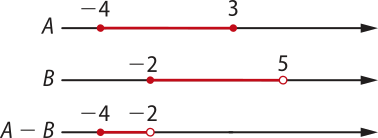
A diferença A − B, segundo o diagrama, é [−4, −2[, quê póde sêr escrita como {x ∈ ℝ | −4 ≤ x < −2}.
Resposta: alternativa a.
10. • Falsa. O número 3,14159265 é uma aproximação para o número irracional indicado pela letra grega (pi)". A representação correta seria 3,14159265... (com as reticências).
• Falsa. O conjunto dos números racionais e o dos irracionais não possuem nenhum ponto em comum.
• Verdadeira. Toda dízima periódica é um número racional, pois póde sêr representada como uma fração.
Resposta: alternativa d.
11.
a) Falsa. A quantidade de habitantes de uma cidade é um número natural, pois está associada à contagem.
b) Falsa. A medida da altura de uma pessoa é um número racional, pois póde havêer casas decimais.
c) Falsa. A velocidade média de um veículo é um número racional, porém póde sêr positivo.
d) Verdadeira. O valor pago, em reais, é representado com casas decimais; logo, é um número racional positivo.
e) Falsa. A medida do lado de um triângulo póde sêr um número irracional, porém necessariamente positivo.
Resposta: alternativa d.
Capítulo 2 • Noções de Estatística
Atividades
1. De acôr-do com as informações do qüadro, concluímos:
I. Falsa, pois o número de pessoas quilombolas em Arraias é 1.572, enquanto o número de pessoas em Mateiros é 1.190.
II. Falsa, pois o percentual de pessoas quilombolas em Aragominas é 15,67%, enquanto o percentual em São Félix do Tocantins é 38,25%.
III. Correta, pois o percentual de pessoas quilombolas em Mateiros é 43,30%.
Resposta: alternativa c.
2.
a) Os dados coletados são quantitativos, pois são resultados de uma medida.
b) Organizando os dados em ordem crescente, temos: 120; 131; 137; 144; 149; 151; 160; 163; 170; 172; 179; 181; 181; 187; 188; 189; 192; 193; 193; 199; 202; 205; 205; 210; 211; 217; 220; 226; 234; 239.
c) A amplitude total é calculada pela diferença entre o maior valor e o menor valor do rol. Dessa forma, fazemos 239 − 120 = 119. Portanto, a amplitude total é 119 km.
d) Com a amplitude total, podemos calcular a quantidade de intervalos de amplitude de 20 km: = 5,95
Logo, teremos 6 intervalos de amplitude de 20 km. Assim, os intervalos e suas respectivas freqüências absolutas serão:
[120; 140[: 120; 131; 137 (3 elementos)
[140; 160[: 144; 149; 151 (3 elementos)
[160; 180[: 160; 163; 170; 172; 179 (5 elementos)
[180; 200[: 181; 181; 187; 188; 189; 192; 193; 193; 199 (9 elementos)
[200; 220[: 202; 205; 205; 210; 211; 217 (6 elementos)
[220; 240[: 220; 226; 234; 239 (4 elementos)
Dessa forma, as freqüências relativas são calculadas da seguinte maneira:
[120; 140[: = 0,1 ⇒ 10%
[140; 160[: = 0,1 ⇒ 10%
[160; 180[: = 0,167 ⇒ 16,7%
[180; 200[: = 0,3 ⇒ 30%
[200; 220[: = 0,2 ⇒ 20%
[220; 240[: = 0,133 ⇒ 13,3%
Coletando todas as informações, construímos a tabéla de freqüência:
km |
FA |
FR |
|---|---|---|
[120; 140[ |
3 |
10% |
[140; 160[ |
3 |
10% |
[160; 180[ |
5 |
16,7% |
[180; 200[ |
9 |
30% |
[200; 220[ |
6 |
20% |
[220; 240[ |
4 |
13,3% |
Total |
30 |
100% |
Página trezentos e sessenta e sete
e) De acôr-do com a tabéla de freqüências, concluímos:
I. Falsa. Em apenas 10 dos 30 dias, o motorista rodou mais do quê 200 km.
II. Falsa. O motorista rodou menos do quê 180 km em 36,7% dos dias, pois: 10% + 10% + 16,7% = 36,7%
III. Verdadeira. O motorista rodou em 30% dos dias de 180 a 200 km e, em 20% dos dias, de 200 a 220 km.
Portanto, a afirmação verdadeira é III.
3. O menor comprimento de barra indica a categoria com o menor índice de imunização; nesse caso, apenas aproximadamente 40% dos adultos entre 20 e 29 anos estão imunizados. Resposta: alternativa d.
4. Observe quê, para cada ano, para cada olimpíada, há 100 bó-linhas. Portanto, cada bó-linha vale 1%.
a) Como há apenas 4 bó-linhas amarelas, a porcentagem de mulheres quê era esperada nas Olímpiadas de Paris, em 1924, foi 4%.
b) De acôr-do com o gráfico, a porcentagem de homens nas Olimpíadas de 2016 era 55%, pois no gráfico há 55 bó-linhas pretas.
c) O percentual de participação das mulheres nas Olimpíadas de Paris, em 2024, foi de 49,14%; portanto, próximo de 50%.
5. De acôr-do com o gráfico observa-se quê, de 2005 a 2009, o aumento do volume de vendas foi de 283,2 milhões, pois 519,2 − 236 = 283,2. Dessa forma, a razão entre 283,2 milhões de vendas e 236 milhões de vendas (número de vendas em 2005), expressa em porcentagem desejada:
= 1,2 ⇒ aumento de 120%
Resposta: alternativa c.
6. De acôr-do com o gráfico quê ilustra a quantidade de cirurgias totais, sabemos quê 45% das 800 cirurgias foram realizadas no fêmur. Assim, calculando 45% de 800, tem-se:
0,45 ⋅ 800 = 360
Ou seja, foram realizadas 360 cirurgias no fêmur.
Agora, observando o gráfico de cirurgias realizadas em homens, vemos quê 40% das 440 cirurgias feitas em homens foram do fêmur, o quê corresponde a 176 cirurgias, pois 0,40 ⋅ 440 = 176.
Logo, a quantidade de cirurgias do fêmur realizadas em mulheres é 184, pois 360 − 176 = 184.
Resposta: alternativa c.
7. O professor escolheu o gráfico de linha para analisar a variação do dólar, pois esse gráfico ilustra, por meio de uma linha, a variação temporal de fenômenos, quê, nesse caso, permite observar quando o preêço do dólar aumentou e quando diminuiu.
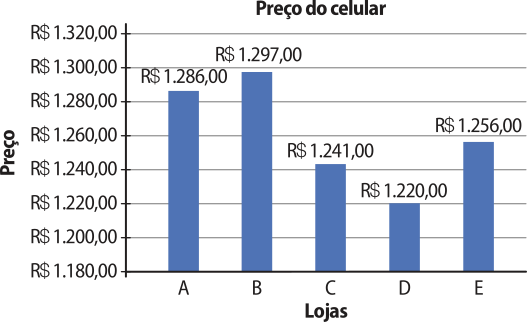
8. a) O gráfico de barras é o mais adequado, porque cada preêço é representado por um comprimento de barra; nesse caso, comparamos os preços pêlos comprimentos das barras.
b)
9.
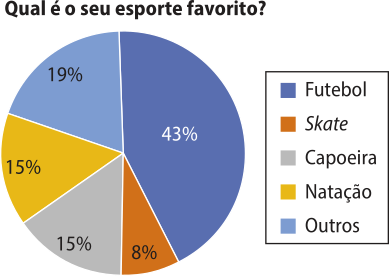
a) O êrro é quê a soma dos percentuais resulta em 106%. Em um gráfico de setores, a soma das porcentagens de todos os setores deve resultar em 100%.
b)
10. Resposta pessoal. Espera-se quê os estudantes pesquisem informações quê comprovem o quanto a participação das mulheres na vida pública evoluiu pouco, mesmo quê elas representem a maioria entre os eleitores.
11. Resposta pessoal. Uma resposta possível é quê, se toda a renda fosse distribuída igualmente entre os trabalhadores brasileiros, em dezembro de 2023, cada um receberia R$ 3.100,00.
12. Calculando a média salarial de cada setor, temos:
I: = 1.245
II: = 1.230
III: = 1.425
IV: = 1.255
V: = 1.250
Logo, o setor quê apresenta a menor média salarial é o Setor II.
Resposta: alternativa b.
13. A média mensal das vendas do comércio de Cláudio póde sêr calculada da seguinte forma:
= 8,75.
Logo, a média de vendas é 8,75 mil reais.
Resposta: alternativa c.
14. Utilizando as informações do gráfico de setores, calculamos as quantidades de alunos dessa escola quê têm 15, 16 e 17 anos, respectivamente:
15 anos: 0,25 ⋅ 80 = 20 ⇒ 20 alunos
16 anos: 0,30 ⋅ 80 = 24 ⇒ 24 alunos
17 anos: 0,45 ⋅ 80 = 36 ⇒ 36 alunos
A média das idades dos 80 alunos dessa escola póde sêr calculada pela seguinte média ponderada:
= 16,2
Resposta: alternativa d.
15. Colocando os dados em rol, temos:
154; 159; 160; 165; 169; 171; 174; 174; 174; 178; 179; 180; 180; 181; 185; 188; 195; 195
A mediana Md é a média aritmética entre 174 e 178, pois há 18 dados:
Md = = 176
Página trezentos e sessenta e oito
A (Moda) Mo é a altura quê mais se repete, ou seja, Mo = 174. Assim, a média aritmética x ̅ entre a (Moda) e a mediana é:
= = 175
Logo, as afirmações I, III e IV são verdadeiras.
Resposta: alternativa c.
16. De acôr-do com os dados do gráfico, podemos calcular a média x ̅ , a (Moda) Mo e a mediana Mo.
A média dos dados é ôbitída por meio da seguinte média ponderada:
= = 4,15625
A (Moda) é Mo = 3, pois é o número de viagens quê mais se repete.
A mediana Md será a média aritmética dos 80º e 81º dados, pois ocorreram 160 viagens.
Md = = 4
Logo, Mo < < Md.
Resposta: alternativa d.
17. I. Verdadeira, pois se não houvesse estudante com altura maior do quê 1,68 m, a média seria inferior a esse valor. Raciocínio semelhante póde sêr feito para o caso de havêer um estudante com menos de 1,68 m de altura.
II. Falsa, pois os dados são insuficientes para afirmar com certeza quê há mais de um estudante nas condições dadas.
18. A soma das áreas dos retângulos do histograma é:
5 ⋅ (6 + 8 + 11 + 15 + 24 + 14 + 10 + 7 + 5) = 500
Assim, cada uma das duas regiões terá 250 unidades de área (metade de 500). Além díssu, sabemos quê a mediana M encontra-se no 5º intervalo, logo:
5 ⋅ 6 + 5 ⋅ 8 + 5 ⋅ 11 + 5 ⋅ 15 + (M − 165) ⋅ 24 = 250 ⇒ 200 + (M − 165) ⋅ 24 = 250 ⇒ M = + 165 ≃ 167,08
Portanto, a abscissa do ponto M é aproximadamente 167,08.
19. Calculando a média do estudante, tem-se:
= ⇒ 5 = ⇒ y = 4,5
Portanto, a nota mínima para sêr aprovado é 4,5.
20. Para quê o gerente permaneça no cargo, a média deve sêr de, no mínimo, 30 mil reais. Assim, calcula-se a média igualando-a a 30 mil.
30 = ⇒ 145 + x = 180 ⇒ x = 35
Resposta: alternativa e.
21. Como os dados estão em um histograma, por convenção, tanto para o cálculo da média quanto da (Moda) consideramos os pontos médios de cada intervalo.
a) O tempo médio é calculado da seguinte forma:
= 151,3462
O tempo médio de espera foi de, aproximadamente, 151,3 minutos.
b) A (Moda) é calculada da seguinte forma:
= 152,5
Logo, a maioria das pessoas esperou 152,5 minutos na fila.
22. a) Resposta pessoal.
b) Resposta pessoal.
c) Espera-se quê os estudantes citem as kestões financeiras e o equilíbrio entre vida profissional e maternidade.
23.
a) Espera-se quê os estudantes percêbam quê no mapa de 2022 as tonalidades de todas as regiões são mais escuras quê no mapa de 2010, indicando quê a idade mediana aumentou em todas as Unidades da Federação.
b) Não. Em todos os locais indicados a idade mediana aumentou
c) Aumentou 6 anos.
d) Resposta pessoal.
e) Resposta pessoal.
24. O tempo médio de cada atleta foi:
Atleta 1: = 120
Atleta 2: = 120
a) O desvio médio de cada atleta foi:
Atleta 1: dm1 = = 4,4
Atleta 2: dm2 = = 2,4
Página trezentos e sessenta e nove
b) A variância e o desvio padrão do atleta 1 foram:
Va1 = = 34,8
Dp1 = ≃ 5,9
A variância e o desvio padrão do atleta 2 foram:
Va2 = = 9,2
Dp2 = ≃ 3,03
c) O atleta 2 teve uma perfórmance mais regular nas cinco corridas, porque tanto o desvio médio quanto o desvio padrão do atleta 2 foram inferiores aos desvios médio e padrão do atleta 1.
25. a) A amplitude de cada lâmpada foi:
Marca 1: A1 = 48 − 28 = 20
Marca 2: A2 = 49 − 26 = 23
Para calcular o desvio médio de tempo de duração de cada lâmpada, calculamos inicialmente as médias:
Marca 1: = 37
Marca 2: = 37
Assim, o desvio médio de cada marca foi:
Marca 1: dm1 = = 6
Marca 2: dm2 = = 8
Já a variância e o desvio padrão foram:
Marca 1: Dp1 = = ≃ 6,99
Marca 2: Dp2 = = ≃ 8,65
b) A marca 1 apresentou os melhores resultados, pois sua amplitude foi de 20 mil horas e seu desvio médio e seu desvio padrão foram inferiores à lâmpada da marca 2, o quê indica quê a distribuição dos tempos estimados de uso da lâmpada da marca 2 são mais próximos do tempo médio de duração de 37 mil horas.
26. Resposta pessoal. Um aluno póde preferir a empresa X, porque ela paga os maiores e os menóres salários. Nesse caso, se ele seguir carreira dentro da empresa receberá salários maiores do quê a empresa Z. Por outro lado, um aluno póde escolher a empresa Z, pois a chance de receber salário próximo de R$ 9.000,00 é maior do quê na outra empresa.
27. Como a média de tempo das cinco equipes é a mesma, a equipe campeã é determinada pelo menor desvio padrão pois, isso indica quê seus tempos foram os quê mais se aproximaram do tempo médio de cada próva. Dessa forma, a equipe campeã foi a equipe III.
Resposta: alternativa c.
28. a) Resposta pessoal. b) Resposta pessoal. c) Resposta pessoal. d) Resposta pessoal.
Depois quê os estudantes fizerem os cálculos, é interessante quêstionar sobre o que poderia acontecer com os dados se a altura do professor fosse acrescentada ao conjunto.
29. Resposta pessoal. Exemplo de problema: Ana e Maria fazem um curso de língua inglesa. Ao longo de um ano, elas realizaram quatro provas, cujas notas são apresentadas a seguir:
Ana |
75 |
96 |
85 |
70 |
|---|---|---|---|---|
Maria |
86 |
65 |
98 |
77 |
Determine a amplitude das notas de Ana e de Maria.
A amplitude é dada pela diferença entre a maior e a menor nota de cada uma. Assim:
Ana: 96 − 70 = 26
Maria: 98 − 65 = 33
Página trezentos e setenta
30. a) Ao organizar os dados em um diagrama de ramos e fô-lhas, obtém-se:
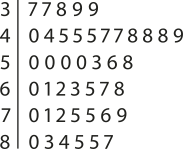
b) Como o conjunto de dados tem número ímpar de elemêntos a mediana é o termo central (22°), ou seja, 56.
A (Moda) é o elemento quê mais se repete, nesse caso, 50.
c) Quem acertou 70 kestões ou mais, ou seja, 3 + 4 + 3 + 3 =
= 13 estudantes.
≃ 0,3023 ⇒ aproximadamente 30,23%
d)
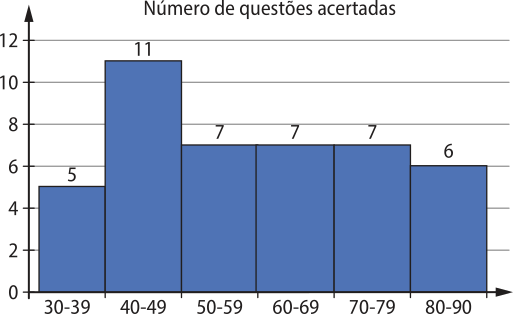
Fonte: Dados fictícios.
e) Resposta pessoal. Espera-se quê os estudantes percêbam quê as duas representações são adequadas, dependendo da intenção de quem está fazendo o gráfico. O histograma permite visualizar de maneira mais imediata a freqüência de cada intervalo, já o diagrama de ramo e fô-lhas preserva cada dado da amostra.
31. a) Observando o box-plot, é possível concluir quê o mais novo tem 21 anos e o mais velho, 55 anos.
b) Sim. Resposta esperada: O terceiro quartil indica quê 25%
dos dados estão acima dele, portanto 75% estão abaixo.
c) Há mais estudantes entre 46 e 55 anos. Resposta esperada:
É possível concluir isso, porque a linha do terceiro quartil até o valor mássimo é maior do quê a linha do primeiro quartil até o valor mínimo.
d) O número 37 indica quê mêtáde dos estudantes tem idade abaixo de 37 anos; a outra mêtáde, acima de 37 anos.
32. Resposta pessoal. Exemplo de problema: qual é a amplitude do diagrama?
Como a amplitude de um conjunto de dados é a diferença entre o maior e o menor valor, tem-se: 77 − 40 = 34
33. Para elaborar o box-plot, inicialmente, organizam-se os dados em ordem crescente para identificação dos valores necessários.
37, 37, 38, 39, 39, 40, 44, 45, 45, 45, 47, 47, 48, 48, 48, 49, 50, 50, 50, 50, 53, 56, 58, 60, 61, 62, 63, 65, 70, 71, 72, 75
Como o conjunto tem 32 dados, a mediana é dada pela média aritmética dos termos centrais, ou seja, Md = = 49,5.
O primeiro quartil é o termo central dos valores à esquerda da mediana, ou seja, Q1 = 45.
O terceiro quartil é o termo central dos valores à direita da mediana, ou seja, Q3 = 60,5.
Calculando os limites inferiores e superiores, tem-se: Limite inferior: Q1 − 1,5(Q3 − Q1)= 45 − 1,5(60,5 − 45) =
= 45 − 23,25 = 21,75
Limite superior: Q3 + 1,5(Q3 − Q1)= 60,5 + 1,5(60,5 − 45) =
= 60,5 + 23,25 = 83,75
Observar quê tanto o valor mínimo da amostra (37) quanto o valor mássimo (75) estão dentro dos limites inferior e superior, respectivamente.
Então, tem-se:
Valor mínimo |
37 |
|---|---|
Q1 |
45 |
Q2 (mediana) |
49,5 |
Q3 |
60,5 |
Valor mássimo |
75 |
Com base nos valores do qüadro, pode-se construir o seguinte box-plot:
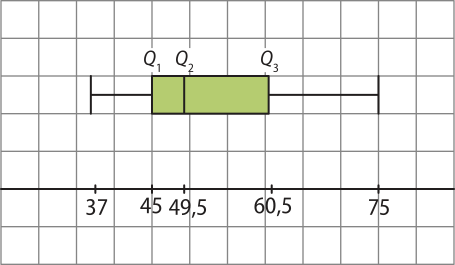
Resposta pessoal. Exemplos de perguntas:
1. Qual é a média dos valores situados entre o primeiro e o terceiro quartil?
Os valores entre o primeiro e o terceiro quartil são:
47, 47, 48, 48, 48, 49, 50, 50, 50, 50, 53, 56, 58 e 60. Logo, a média será:
= 51
2. Qual é a amplitude da amostra?
A amplitude da amostra é a diferença entre o maior e o menor valor, ou seja:
75 − 37 = 38
A amplitude é de 38 kg.
Atividades complementares
1. Seja x a quantidade total de perfumes vendidos no mês de novembro. De acôr-do com os gráficos, temos quê a arrecadação em espécie póde sêr calculada da seguinte maneira:
Perfume I: 0,13 ⋅ x ⋅ 200 = 26x
Perfume II: 0,10 ⋅ x ⋅ 170 = 17x
Perfume III: 0,16 ⋅ x ⋅ 150 = 24x
Perfume IV: 0,29 ⋅ x ⋅ 100 = 29x
Perfume V: 0,32 ⋅ x ⋅ 80 = 25,6x
Como x representa uma quantidade, o perfume quê gerou mais arrecadação foi o perfume IV.
Resposta: alternativa d.
2. De acôr-do com o gráfico, analisamos as informações.
a) Falsa, pois o Distrito Federal teve o maior decréscimo no período entre 2014 e 2017.
b) Falsa, pois Santa Catarina apresentou um número maior em 2017 do quê em 2007.
c) Falsa, pois em 2017, a taxa do Brasil foi aproximadamente de 5 homicídios a cada 100 mil mulheres, enquanto a soma das taxas das três unidades federativas foi aproximadamente de 8 homicídios a cada 100 mil mulheres.
d) Falsa, pois o gráfico não mostra todos os estados da Região Sul do Brasil. Por isso, não é possível afirmar quê a taxa de Santa Catarina superou as taxas dos demais estados dessa região.
e) Verdadeira.
Resposta: alternativa e.
Página trezentos e setenta e um
3. Lembrando quê a circunferência completa tem um ângulo de 360° e tendo em conta quê o turno da manhã representa 40% da circunferência, a medida do ângulo (alfa)" correspondente ao turno da manhã é:
(alfa)" = 0,40 ⋅ 360° = 144°
Resposta: alternativa a.
4. Como a quantidade de estudantes é par, a nota mediana é dada pela média entre a 15ª e a 16ª maiores notas, ou seja, 6,0 e 8,0, respectivamente. Logo, a nota mediana é:
= 7,0
Resposta: alternativa b.
5. Sejam y, z e w as três notas cuja média é 8,0 e x a nota quê se repete. De acôr-do com as informações do enunciado, temos:
= 7,0 ⇒ y + z + w = 21,0
Assim:
= 8,0 ⇒ 2x + y + z + w = 40,0 ⇒
⇒ 2x = 40,0 − 21,0 = 19,0 ⇒ x = 9,5
Resposta: alternativa b.
6. De acôr-do com o gráfico de barras, podemos calcular a média mensal de mortes violentas na comunidade LGBTQIA+ da seguinte forma:
= 25
Assim, a média mensal foi de 25 mortes violentas no Brasil da comunidade LGBTQIA+ em 2021.
7. De acôr-do com o gráfico, vemos quê há cinco estudantes com massa corporal maior do quê 80 kg. Destes cinco estudantes, apenas dois deles têm a medida de altura acima da média, quê é 1,65 m. Logo:
= 0,20 ⇒ 20%
Ou seja, 20% dos estudantes têm as medidas de massa corporal e altura acima das médias.
Resposta: alternativa b.
8. a) A porcentagem p aproximada de alunos quê tiraram nota menor ou igual a 7 foi:
p = ≃ 0,13 ⇒ 13%
A quantidade q de alunos quê tiraram notas maiores do quê 8 foi:
q = 253 = ⋅ 253 = 121
Logo, 121 alunos tiraram notas maiores quê 8.
b) A média M das notas foi, aproximadamente:
M = = ≃ 8,02
A nota mediana Me das notas foi, aproximadamente:
3 + 9 ⋅ (Me -7) = ⇒
⇒ 3 + 9Me − 63 = ⇒
⇒ 9Me = 71,5 ⇒
⇒ Me ≃ 7,94
9. O atleta mais regular é aquele cujo desvio padrão é o menor entre todos. Nesse caso, o atleta mais regular é o atleta III.
Por outro lado, o atleta menos regular é aquele cujo desvio padrão é o maior entre todos. Assim, o atleta menos regular é o atleta II.
Logo, a primeira luta será entre os atletas II e III.
Resposta: alternativa c.
10. Estabelecendo a mediana e a (Moda), tem-se:
Md = = = 34
Mo = 33
34 + 33 = 67
Resposta: alternativa a
11. I. Verdadeira. Observando o primeiro box-plot, tem-se quê o peso mediano estava acima de 89 kg.
II. Verdadeira. O terceiro quartil em 93 kg indica quê 25% dos pacientes pesam 93 kg ou mais.
III. Falsa. O valor 84 kg está mais próximo do primeiro quartil, o quê indica um total de aproximadamente 25% dos pacientes pesando menos do quê 84 kg.
IV. Falsa. Como o primeiro e o terceiro quartis estão entre 83 kg e 87 kg, tem-se quê isso corresponde a aproximadamente 50% dos pacientes.
Resposta: alternativa b.
Capítulo 3 • Introdução às funções e função afim
Atividades
1. a) O número de barras de chocolate é a variável independente, pois uma pessoa póde comprar quantas quiser. O preêço a sêr pago é a variável dependente, pois o valor final depende da quantidade de barras compradas.
b) O andar do apartamento em quê uma pessoa mora é a variável independente, pois uma pessoa póde morar no andar quê desejar. O tempo gasto para o elevador chegar ao apartamento é a variável dependente, pois o tempo dependerá do andar em quê a pessoa mora.
2. O enunciado da atividade afirma quê há uma relação entre as variáveis s e t e, como o objetivo da questão é descobrir qual é a relação algébrica entre essas variáveis, uma estratégia é substituir um valor de t nas relações e eliminar aquelas quê apresentam uma resposta diferente da tabéla.
Assim, ao considerar t = 1, deve-se obtêr s = 0. A alternativa d apresenta uma resposta diferente, pois, ao resolver a equação s = t2, considerando t = 1, obtém-se s = 1. Portanto, não póde sêr essa alternativa.
Ao considerar t = 2, deve-se obtêr s = 3. Porém, as alternativas a e b apresentam respostas diferentes, pois, ao resolver a equação, s = 2t − 2, considerando t = 2, obtém-se s = 2, e, ao resolver a equação s = t − 1, obtém-se s = 1. Logo, ambas as alternativas, a e b, não estão corretas.
Portanto, por eliminação, resta a alternativa c.
Para conferir a resposta, pode-se substituir os valores de t e s na relação e verificar a resposta:
t = 1 ⇒ s = 12 − 1 = 0
t = 2 ⇒ s = 22 − 1 = 3
t = 3 ⇒ s = 32 − 1 = 8
t = 4 ⇒ s = 42 − 1 = 15
t = 5 ⇒ s = 52 − 1 = 24
Resposta: alternativa c.
3. Como o perímetro é a soma dos lados de um polígono, pode-se concluir quê o perímetro do retângulo é P = 6x. A área do retângulo é o produto entre a base e a altura, portanto, A = x ⋅ 2x = 2x2. A diagonal do retângulo equivale à hipotenusa de um triângulo retângulo cujos catetos médem x e 2x. Portanto, d = = é a medida da diagonal do retângulo.
Página trezentos e setenta e dois
4. Considerando as informações fornecidas pelo enunciado, pode-se observar quê:
x (nº de entrada) |
y (nº de saída) |
|---|---|
0 |
2 ⋅ 0 + 3 = 3 |
1 |
2 ⋅ 1 + 3 = 5 |
2 |
2 ⋅ 2 + 3 = 7 |
3 |
2 ⋅ 3 + 3 = 9 |
4 |
2 ⋅ 4 + 3 = 11 |
5 |
2 ⋅ 5 + 3 = 13 |
x |
2 ⋅ x + 3 |
Considerando o modelo anterior, pode-se concluir quê a = 2 e b = 3 e a fórmula é y = 2x + 3.
5. Considerando quê p representa o número de pães fabricados e t o tempo, em horas, quê se leva para fabricar p pães, pode-se afirmar quê:
a) p = 300t é a lei quê representa essa relação.
b) Em 3 horas e 30 minutos, ou seja, t = 3,5, serão fabricados: p(3,5) = 300 ⋅ 3,5 = 1.050
Em 3 horas e 30 minutos serão fabricados 1.050 pães.
6. Pelo enunciado, tem-se A = {−2, −1, 0, 1}, portanto cada um de seus elemêntos faz parte do domínio de f. Então, a imagem da função deve sêr calculada com base em cada elemento do domínio de f.
a) f(x) = x3, então:
f(−2) = (−2)3 = −8
f(−1) = (−1)3 = −1
f(0) = 03 = 0
f(1) = 13 = 1
Portanto, Im(f) = {−8, −1, 0, 1}.
b) f(x) = −x + 3, então:
f(−2) = −(−2) + 3 = 5
f(−1) = −(−1) + 3 = 4
f(0) = −0 + 3 = 3
f(1) = −1 + 3 = 2
Portanto, Im(f) = {2, 3, 4, 5}.
c) f(x) = 1 − x2, então:
f(−2) = 1 − (−2)2 = −3
f(−1) = 1 − (−1)2 = 0
f(0) = 1 − 02 = 1
f(1) = 1 − 12 = 0
Portanto, Im(f) = {−3, 0, 1}.
7. a) Observe quê a imagem corresponde a cada elemento do domínio acrescido de duas unidades. Assim, uma possível lei de formação é y = x + 2 ou f(x) = x + 2.
b) Observe quê a imagem corresponde a cada elemento do domínio elevado ao quadrado. Assim, uma possível lei de formação é y = x2 ou h(x) = x2.
8. Conforme informação do enunciado, o pintor cobra o valor fixo de 30 reais mais uma quantia quê depende da área pintada. Com base nisso, pode-se organizar a seguinte tabéla:
Área x pintada (em m2) |
Total y a pagar pela pintura (em reais) incluindo a parcela fixa |
Valor fixo (em R$) |
Valor cobrado pela área x pintada (em m2) |
Valor cobrado por m2 pintado (em R$) |
|---|---|---|---|---|
5 |
40 |
30 |
10 |
2 |
10 |
50 |
30 |
20 |
2 |
15 |
60 |
30 |
30 |
2 |
20 |
70 |
30 |
40 |
2 |
30 |
90 |
30 |
60 |
2 |
40 |
110 |
30 |
80 |
2 |
• Falso. Pela tabéla, pode-se afirmar quê o pintor cobra 30 reais mais 2 reais (e não 3 reais) pelo métro quadrado pintado.
• Verdadeiro. Como o pintor cobra 2 reais o métro quadrado pintado, para pintar uma área de 250 m2, ele cobrará 500 reais. Acrescentando a taxa fixa de 30 reais, o valor final será de 530 reais.
• Falso. Seguindo o raciocínio anterior, para pintar uma área de 150 m2, o pintor cobrará 300 reais. Acrescentando a taxa fixa, o valor final será de 330 reais. Portanto, mais do quê 300 reais.
Resposta: alternativa c.
9. a) Como não há nenhuma restrição para valores quê x póde assumir na função h(x) = 4x − 5, então o domínio será D(h) = ℝ.
b) A função j(x) = está definida para 1 + x ≠ 0. Portanto, x não póde assumir os valores −1. Logo, o domínio da função é D(j) = ℝ − {−1}.
c) A condição de existência da função z(x) = é 2x ≥ 0. Portanto, x não póde assumir valores menóres do quê 0. Logo, o domínio da função é D(z) = {x ∈ ℝ | x ≥ 0}.
Página trezentos e setenta e três
10. a) Ao observar a ilustração, pode-se perceber quê a quantidade de palítos é um número múltiplo de 3, quê depende da quantidade de palítos de cada lado. Portanto, pode-se preencher o qüadro da seguinte maneira:
Número de palítos em cada lado |
Total de palítos em cada triângulo |
|---|---|
1 |
3 |
2 |
6 |
3 |
3 ⋅ 3 = 9 |
4 |
3 ⋅ 4 = 12 |
5 |
3 ⋅ 5 = 15 |
6 |
3 ⋅ 6 = 18 |
b) Como a quantidade de palítos é o triplo do número de palítos do lado do triângulo, logo f(x) = 3x ou y = 3x.
c) O domínio da função será os números naturais positivos, ou seja, D(f) = {1, 2, 3, 4, 5, 6,...}. A imagem é composta por todos os números naturais múltiplos de 3 maiores do quê 0, ou seja, Im(f) = {3, 6, 9, 12, 15, 18,...}.
d) Como a construção possui 45 palítos, pode-se afirmar quê y = 45. Portanto, precisa-se descobrir quantos palítos há em cada lado, ou seja, o valor de x. Logo:
y = 3x ⇒ 45 = 3x ⇒ x = 15
Portanto, cada lado deve ter 15 palítos.
11. Resposta pessoal. Ao elaborar um problema quê envolva a construção de um quadrado com palítos de fósforo, espera-se quê o estudante chegue à relação y = 4x para contabilizar a quantidade total de palítos (y) ou, caso se tenha a quantidade total de palítos, encontre a quantidade de palítos quê cada lado possui (x).
12. Segundo enunciado, há uma relação entre a quantidade x de anúncios feitos por uma loja em um período de uma semana e a quantidade y de itens vendidos nesse mesmo período.
Essa relação é estabelecida pela função y = x + 80.
Considerando quê a loja deve vender 200 itens, ou seja, y = 200, então, o número de anúncios deverá sêr:
200 = x + 80 ⇒ 400 = 3x + 160 ⇒ x = 80
Assim, o gerente da loja deverá anunciar 80 vezes durante a semana para vender 200 itens.
13. Conforme a orientação dos eixos ordenados e os pontos localizados nesse sistema cartesiano, pode-se afirmar quê as coordenadas dos pontos são: A(2, 2), B(0, 0), C(5, 0), D(0, 6), E(−3, 0), F(0, −2), G(−2, 4), H(−5, −5), I(5, −3) e J(−5, 1).
14. Como os pares ordenados representam o mesmo ponto, então pode-se afirmar quê os valores das abscissas são iguais, assim como os valores das ordenadas. Logo:
2a − 3 = 5a − 1 ⇒ 2a − 5a = −1 + 3 ⇒ −3a = 2 ⇒ a = b + 2 = 2b − 3 ⇒ b − 2b = −3 − 2 ⇒ b = 5
15. a) Como cada flecha possui um valor para a coordenada, pode-se localizar cada uma delas no plano cartesiano, conforme a imagem a seguir:
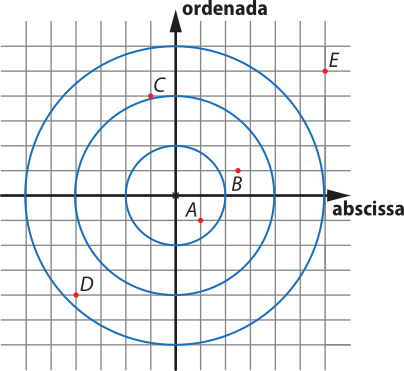
b) No círculo menor, Manoel acertou uma flecha (A).
c) Manoel fez 300 pontos referentes à flecha em A, 100 pontos referentes à flecha em B e mais 100 pontos (duas flechas de 50 pontos) referentes às flechas em C e em D. A flecha em E não rendeu pontos, pois está fora do alvo. Portanto, o total de pontos quê Manoel conquistou ao lançar 5 flechas foi: 300 + 100 + 100 = 500, portanto 500 pontos.
16. O domínio do gráfico de uma função é representado pela projeção de todos os pontos do gráfico sobre o eixo das abscissas, e a imagem é representada pela projeção de todos os pontos, dêêsse mesmo gráfico, sobre o eixo das ordenadas. Com base nisso, tem-se:
a) D(f) = {x ∈ ℝ | −2 ≤ x < 3} e Im(f) = {y ∈ ℝ | −2 ≤ y < 2}
b) D(f) = {x ∈ ℝ | −3 < x < 3} e Im(f) = {y ∈ ℝ | −1 ≤ y ≤ 3}
c) D(f) = {x ∈ ℝ | −3 ≤ x ≤ 4 e x ≠ 1} e Im(f) = {y ∈ ℝ | −2 < y ≤ 3}
d) D(f) = ℝ e Im(f) = ℝ
e) D(f) = ℝ e Im(f) = {y ∈ ℝ | y ≥ 0}
f) D(f) = {x ∈ ℝ | x < 0} e Im(f) = {y ∈ ℝ | y > 0}
17. Para responder às perguntas, deve-se observar o gráfico.
a) A tempera-túra atinge 0°C no instante em quê o gráfico corta o eixo das abscissas; portanto, às 2 h e às 8 h.
b) Os extremos do intervalo em quê a tempera-túra varia se dá pelas tempera-túras mínima e mássima. Assim, a tempera-túra mínima é de −5°C e a mássima é de 13°C. Portanto, a tempera-túra varia de −5°C a 13°C.
c) A tempera-túra é positiva no intervalo em quê o gráfico está acima do eixo da abscissa, ou seja, de 0 h às 2 h e de 8 h às 24 h.
18. a) Considerando x = 27, a numeração será:
y = 1,25x + 7 ⇒ y = 1,25 ⋅ 27 + 7 ⇒ y = 40,75
Arredondando o resultado para o número natural imediatamente maior, obtém-se 41.
b) Resposta pessoal. Considerando, por exemplo, quê a numeração do pé de um estudante seja 40, a medida de seu pé será:
y = 1,25x + 7 ⇒ 40 = 1,25x + 7 ⇒ x = 26,4
A medida do pé deverá sêr inferior ou igual a 26,4 cm, pois, caso contrário, ele deverá calçar 41.
Página trezentos e setenta e quatro
Por outro lado, como esse valor é arredondado para cima, o pé dele póde sêr menor do quê 26,4 cm. Porém, não póde sêr muito menor, pois, caso contrário, ele deveria calçar 39. Considerando quê a medida do pé de uma pessoa quê calça 39 seja:
y = 1,25x + 7 ⇒ 39 = 1,25x + 7 ⇒
⇒ x = 25,6
Então, se um estudante calça número 40, a medida do pé precisa sêr maior do quê 25,6cm e menor ou igual a 26,4cm.
19. As funções afins são escritas na forma f(x) = ax + b, em quê a e b são números reais.
a) Então, as funções II, III e IV são funções afins.
b) II: função polinomial do 1º grau; III: função polinomial do 1º grau e função linear; IV: função constante
c) II) a = −2 e b =
II) a = e b = 0
IV) a = 0 e b = 0,01
20. a) A notação f(2) equivale a dizêr quê x = 2. Então, para calcular o valor solicitado, basta substituir x por 2 na lei da função:
f(2) = 5 ⋅ 2 − 2 ⇒ f(2) = 8
b) A notação f(x) = 0 equivale a dizêr quê y = 0. Então, deve-se igualar a lei da função a zero. Logo:
5x − 2 = 0 ⇒ x =
21. Sendo x o volume, em métro cúbico, de concreto utilizado, então o preêço total do concreto utilizado é:
y = ⋅ x+
Resposta: alternativa d.
22. Como h é uma função afim, pode-se escrevê-la na forma genérica y = ax + b.
Considerando os dados do problema, obtém-se:
h(1) = 4 ⇒ x = 1 e y = 4
Então:
a ⋅ 1 + b = 4 ⇒ a + b = 4 I
h(−2) = 10 ⇒ x = −2 e y = 10
Então:
a ⋅ (−2) + b = 10 ⇒ −2a + b = 10 II
Resolvendo o sistema formado por I e II, temos:
⇒
3a = −6 ⇒ a = −2
Se a = −2, então −2 + b = 4 ⇒ b = 6.
Como a = −2 e b = 6, a função h é dada por h(x) = −2x + 6.
Daí, pode-se calcular:
h = -2 + 6 = 1 + 6 = 7
A função é h(x) = −2x + 6 e
h = 7.
23. Segundo o enunciado, f(x) = ax + 2, porém sabe-se quê f(4) = 20. Portanto, pode-se considerar quê, para x = 4, tem-se y = 20.
Para calcular o valor do coeficiente a, deve-se substituir esses valores na função. Ao fazer isso, obtém-se:
20 = a ⋅ 4 + 2 ⇒ a =
24. a) As fórmulas quê relacionam a quantidade de impressões e o valor pago de cada gráfica são: yA = 0,30x e yB = 0,25x, em quê x representa a quantidade de impressões.
b) Sim, pois, por exemplo, se o número de folhetos impressos triplicar, o valor a sêr pago também triplicará; se o número de folhetos impressos cair pela mêtáde, o valor a sêr pago também cairá pela mêtáde. Isso significa quê o valor pago pela impressão é diretamente proporcional ao número de unidades impréssas.
c) Se Sofia encomendar 1.000 folhetos, então x = 1.000. Logo:
yB = 0,25 ⋅ 1.000 = 250
O valor a sêr pago por 1.000 folhetos será R$ 250,00.
25. Como f é uma função linear, então pode-se considerar quê b = 0.
O enunciado nos informa quê f(−3) = 4, ou seja, x = −3 e y = 4, então:
f(x) = ax ⇒ 4 = a ⋅ (−3) ⇒ a =
Portanto, a função linear é f(x) = x.
Agora, ao calcular f(6), obtém-se:
f(x) = x ⇒ f(6) = ⋅ 6 ⇒ f(6) = −8
26. a) Considerando p o perímetro do retângulo, pode-se escrever quê:
p(x) = 2x + 2 ⋅ (x + 5)
p(x) = 4x + 10
Em quê p é uma função polinomial do 1º grau restrita ao domínio]0, +∞[, pois a medida do lado de qualquer polígono é um número positivo.
b) Ao considerar os valores de x e p(x), descritos a seguir, e substituí-los na função p(x) = 4x + 10, obtêm-se os seguintes valores:
p(5) = 4 ⋅ 5 + 10 = 20
p(10) = 4 ⋅ 10 + 10 = 50
p(20) = 4 ⋅ 20 + 10 = 90
p(30) = 4 ⋅ 30 + 10 = 130
p(x) = 162 ⇒ 4x + 10 = 162 ⇒
⇒ x = = 38
p(x) = 210 ⇒ 4x + 10 = 210 ⇒
⇒ x = = 50
Portanto, completando a tabéla tem-se:
x (em metro) |
p(em metro) |
|---|---|
5 |
30 |
10 |
50 |
20 |
90 |
30 |
130 |
38 |
162 |
50 |
210 |
c) Não, pois a razão não é constante.
d) Como o perímetro méde 78 m, pode-se considerar quê p(x) = 78. Logo:
4x + 10 = 78 ⇒ 4x = 68 ⇒ x = 17
Como o outro lado méde x + 5, então os lados médem 17 m e 22 m.
27. Se f é uma função polinomial do 1º grau, então pode-se escrevê-la, na forma genérica, como f(x) = ax + b. Considerando os dados fornecidos no enunciado, têm-se:
f(3) = 6 ⇒ a ⋅ 3 + b = 6 ⇒ 3a + b = 6 I
f(4) = 8 ⇒ a ⋅ (4) + b = 8 ⇒ 4a + b = 8 II
Resolvendo o sistema formado por I e II:
⇒ ![]()
Se a = 2, então 3 ⋅ 2 + b = 6 ⇒ b = 0.
Assim f(x) = 2x. Daí, podemos calcular f(10):
f(x) = 2x ⇒ f(10) = 2(10) ⇒ f(10) = 20
Resposta: alternativa e.
28. a) Considerando d a distância percorrida, em centímetro, e t o tempo de duração da caminhada, em segundo, pode-se escrever quê a relação entre distância percorrida e tempo é d = 80t.
b) Sim, são grandezas diretamente proporcionais, pois a razão é igual a 80.
c) Caso a pessoa caminhe por 10 s:
d = 80 ⋅ 10 = 800
Ela percorrerá, em 10 s, 800 cm ou 8 m.
Agora, caso a pessoa caminhe por 40 s:
d = 80 ⋅ 40 = 3.200
Ela percorrerá, em 40 s, 3.200 cm ou 32 m.
Página trezentos e setenta e cinco
d) Como 100 m equivalem a 10.000 cm, então:
10.000 = 80 t ⇒ t = = 125
Portanto, essa pessoa levará 125 s para percorrer 100 m.
29. Considerando os dados fornecidos pelo enunciado, pode-se escrever:
f(x) = ax + b e f(1) = −9 ⇒ a + b = −9
Como b2 − a2 é uma diferença entre dois quadrados, é possível escrevê-lo na forma fatorada (b + a)(b − a). Como a + b = b + a =−9, tem-se:
b2 − a2 = (b + a)(b − a) ⇒
⇒ 54 = −9 ⋅ (b − a) ⇒
⇒ (b − a) = −6 ⇒ a − b = 6
30. A lei da função quê modela o experimento póde sêr considerada da forma y = ax + b, sêndo y o nível da á gua e x o número de bolas. Tomando os valores fornecidos pelo qüadro e aplicando-os na fórmula da função, pode-se obtêr o seguinte sistema:
Subtraindo a primeira equação da segunda, obtém-se:
6,70 − 6,35 = 10a − 5a + b − b ⇒
⇒ 5a = 0,35 ⇒ a = 0,07
Substituindo esse valor em qualquer uma das equações, obtém-se b = 6.
Portanto, a lei da função é y = 0,07x + 6.
Resposta: alternativa e.
31. a) Considerando os valores x = 0 e x = 1 para a função f(x) = 2x + 1, obtém-se:
x |
f(x) |
|---|---|
0 |
1 |
1 |
3 |
Portanto, tem-se os seguintes pares ordenados (0, 1) e (1, 3) quê pertencem à função. Assim, ao inserir esses pontos no plano cartesiano e traçar a reta quê passa por eles, obtém-se:
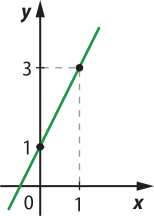
b) Considerando os valores x = 0 e x = 1 para a função g(x) = −x + 4, obtém-se:
x |
g(x) |
|---|---|
0 |
4 |
1 |
3 |
Portanto, tem-se os seguintes pares ordenados (0, 4) e (1, 3) quê pertencem à função. Assim, ao inserir esses pontos no plano cartesiano e traçar a reta quê passa por eles, obtém-se:
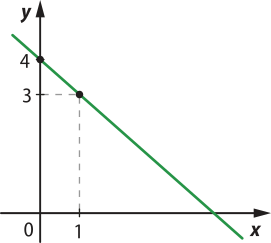
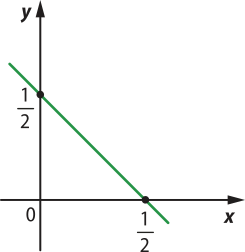
c) Considerando os valores x = 0 e x= para a função y = − x, obtém-se:
x |
y |
|---|---|
0 |
|
0 |
Portanto, tem-se os seguintes pares ordenados quê pertencem à função. Assim, ao inserir esses pontos no plano cartesiano e traçar a reta quê passa por eles, obtém-se:
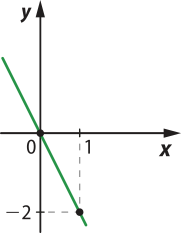
d) Considerando os valores x = 0 e x = 1 para a função h(x) = −2x, obtém-se:
x |
h(x) |
|---|---|
0 |
0 |
1 |
−2 |
Portanto, tem-se os seguintes pares ordenados (0, 0) e (1, −2) quê pertencem à função. Assim, ao inserir esses pontos no plano cartesiano e traçar a reta quê passa por eles, obtém-se:
32. Na função f(x) = ax + b, o valor b é a ordenada do ponto em quê o gráfico intercepta o eixo y. Como p − 2 representa o coeficiente linear b, temos:
p − 2 = 4 ⇒ p = 6
33. Na função polinomial f(x) = ax + b, o gráfico intercepta o eixo das abscissas quando f(x) = 0. Portanto, considerando os dados fornecidos pela atividade, pode-se concluir quê f(3) = 0. Logo:
f(3) = 0 ⇒ −2 ⋅ 3 + 4m + 5 = 0 ⇒
⇒ m =
34. Para determinar o zero de uma função, deve-se calcular f(x) = y = 0. Assim, para cada caso, tem-se:
a) f(x) = −3x + 4
f(x) = 0 ⇒ −3x + 4 = 0 ⇒ x =
b) y = x
y = 0 ⇒ x = 0 ⇒ x = 0
c) y = 2x + 8
y = 0 ⇒ 2x + 8 = 0 ⇒ x = −4
d) y = 6 +
y = 0 ⇒ 6 + = 0 ⇒ x = −24
35. Sabe-se quê o custo total da fabricação de um artigo é R$ 45,00 por unidade, mais um custo fixo de R$ 2.000,00.
a) Considerando os dados do enunciado, pode-se definir quê a função quê representa o custo total é dada por f(x) = 45x + 2.000, em quê x representa a quantidade de peças fabricada.
b) O custo de fabricação de 10 unidades é o valor de f(10). Logo:
f(10) = 45 ⋅ 10 + 2.000 ⇒ f(10) = 2.450
Portanto, o custo de fabricação de 10 peças será R$ 2.450,00.
c) Afirmar quê o custo total é R$ 3.800,00 equivale a dizêr quê f(x) = 3.800. Portanto, para saber o número de peças quê gerou esse custo, deve-se resolver a equação:
3.800 = 45x + 2.000 ⇒
⇒ 45x = 1.800 ⇒ x = 40
Portanto, a produção de 40 unidades gerará um custo total de R$ 3.800,00.
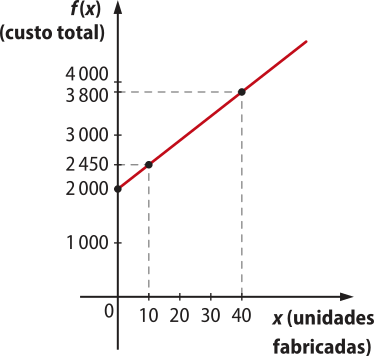
d) Nota-se quê o ponto (0, 2.000) faz parte do gráfico, pois f(0) = 2000. Outros pontos quê compõem o gráfico, de acôr-do com os item b e c, são (10, 2.450) e (40, 3.800). Portanto, destacando esses pontos, tem-se o
Página trezentos e setenta e seis
Observa-se quê o gráfico da função custo total é formado por pontos, e não por um segmento contínuo, pois o domínio da função é o conjunto ℕ. No entanto, todos esses pontos estarão sobre a semirreta quê representa o gráfico da função y = 45x + 2.000 cujo domínio é ℝ+.
36. Como os gráficos de f e g são retas, ambas as funções são polinomiais do 1º grau e podem sêr expressas por y = ax + b.
Para determinar a lei de formação de uma função afim, precisa-se de dois pontos pertencentes ao gráfico da função para substituir na lei e determinar os valores dos coeficientes a e b.
O gráfico da função f passa pêlos pontos (4, 0) e (0, 4).
Então:
⇒
Substituindo o valor de b encontrado em II na equação I, tem-se:
4a + 4 = 0 ⇒ 4a = −4 ⇒ a = −1
Portanto, a lei de formação da função f é f(x) = −x + 4.
Já o gráfico da função g passa pela origem (0, 0), então ela é uma função linear e póde sêr expressa por g(x) = ax, já quê b = 0.
Para x = 2, a ordenada de f(x) é igual à ordenada de g(x), pois é o ponto em quê as duas retas se cruzam. Então:
f(2) = −2 + 4 = 2
Logo, o gráfico de g passa pelo ponto (2, 2). Então:
g(x) = ax ⇒ 2 = 2a ⇒ a = 1
Portanto, g(x) = x.
Assim, as leis de formação das funções são f(x) = −x + 4 e g(x) = x.
37. Observando o gráfico, pode-se considerar quê os pontos (1, 20) e (5, 60) pertencem à função, pois são pontos do gráfico.
a) Para determinar a lei de formação da função y = ax + b, deve-se utilizar os pontos em um sistema, conforme a seguir:
Subtraindo a primeira equação da segunda, obtém-se a = 10. Substituindo esse resultado na primeira equação, obtém-se b = 10.
Portanto, a lei de formação da função definida pelo gráfico é y = 10x + 10.
b) Considerando o sétimo ano, ou seja, x = 7 e substituindo na função, obtém-se:
y = 10x + 10 ⇒ y = 10 ⋅ (7) + 10 ⇒
⇒ y = 80
Portanto, a projeção de vendas do sétimo ano será de R$ 80.000,00.
c) Sim. Espera-se quê os estudantes indiquem quê são necessários apenas dois pontos sobre a reta para determinar a lei de formação da função representada pelo gráfico e quê pontos fora da reta não puderam sêr utilizados.
38. Para identificar se uma função é decrescente, constante ou crescente, deve-se analisar o coeficiente a de cada um dos itens e verificar se é negativo, nulo ou positivo, respectivamente.
a) y = x + 1 → crescente, pois a = , ou seja, positivo.
b) y = −2x + 3 → decrescente, pois a = −2, ou seja, negativo.
c) f(x) = → constante, pois a = 0, ou seja, nulo.
d) f(x) = 3,5 − 0,4x → decrescente, pois a = −0,4, ou seja, negativo.
e) y = −5x → decrescente, pois a = −5, ou seja, negativo.
f) f(x) = −6 → constante, pois a = 0, ou seja, nulo.
39. a) A função é decrescente, pois a inclinação da reta é no sentido descendente. Observa-se quê, à medida quê os valores de x aumentam, os valores de f(x) diminuem.
b) Como a função é uma reta, ela é da forma f(x) = ax + b; então, ao tomar os pontos (0, 3) e (6, 0), é possível obtêr o sistema:
Da primeira equação, obtém-se b = 3, e substituindo esse valor na segunda equação, obtém-se a = .Desse modo, tem-se:
f(x) = x + 3.
c) Ao calcular o zero da função f(x) = x + 3, obtém-se x = 6. Como f é uma função decrescente, pois a < 0, então:
f(x) > 0 para x < 6; f(x) < 0 para x > 6;
f(x) = 0 para x = 6.
40. a) Para mostrar quê f é uma função afim, é necessário desenvolver os produtos notáveis e a fatoração existentes na função. Logo:
f(x) = x(3 − x) + (x − 1)2 ⇒
⇒ f(x) = 3x − x2 + x2 − 2x + 1 ⇒
⇒ f(x) = x + 1
Portanto, f é uma função polinomial do 1º grau.
b) Para calcular o zero da função, deve-se calcular f(x) = 0. Logo:
f(x) = 0 ⇒ x + 1 = 0 ⇒ x = −1
c) f(x) > 0 ⇒ x + 1 > 0 ⇒ x > −1 ⇒
⇒ S = {x ∈ ℝ | x > −1}
41. a) Como a = 1, a função f é crescente. Calculando o zero da função, obtém-se: x + 5 = 0 ⇒ x = −5
Com base nessas informações, pode-se construir o seguinte esboço:
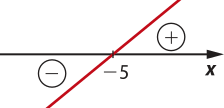
Portanto, tem-se:
f(x) = 0 para x = −5;
f(x) > 0 para x > −5;
f(x) < 0 para x < −5.
b) Como a = −3, a função y é decrescente.
Calculando o zero da função, obtém-se: −3x + 9 = 0 ⇒ x = 3
Com base nessas informações, pode-se construir o seguinte esboço:
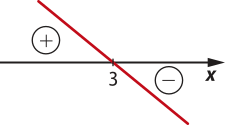
Portanto, tem-se:
y = 0 para x = 3;
y > 0 para x < 3;
y < 0 para x > 3.
c) Como a = , a função y é crescente. Calculando o zero da função, obtém-se: − 1 = 0 ⇒ x = 3
Com base nessas informações, pode-se construir o seguinte esboço:
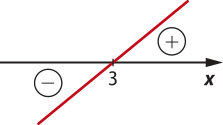
Portanto, tem-se:
y = 0 para x = 3;
y > 0 para x > 3;
y < 0 para x < 3.
d) Como a = , a função f é decrescente.
Calculando o zero da função, obtém-se: 2 − =0 ⇒ x = 4
Com base nessas informações, pode-se construir o seguinte esboço:
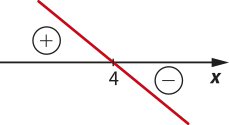
Portanto, tem-se:
f(x) = 0 para x = 4;
f(x) > 0 para x < 4;
f(x) < 0 para x > 4.
42. Segundo os dados fornecidos pelo enunciado, o zero da função é x = −3 e a função passa pelo ponto (1, 2).
a) O gráfico passa pêlos pontos (−3, 0) e (1, 2). Plotando esses pontos no plano cartesiano e sabendo quê a função é afim, tem-se:
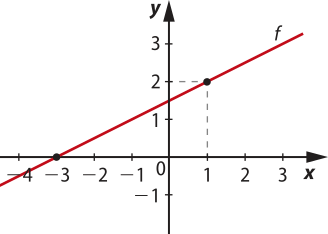
b) Como a função é afim, ela é da forma f(x) = ax + b, então, tomando os pontos (−3, 0) e (1, 2), é possível construir o sistema a seguir:
Página trezentos e setenta e sete
Subtraindo a primeira equação da segunda, obtém-se a = . Substituindo o valor de a em qualquer uma das equações, obtém-se b = . Logo: f(x) = +
c) A partir do zero da função, é possível estudar o sinal da função. Com base no gráfico do item a e considerando quê a função é crescente, obtêm-se:
f(x) = 0 para x = −3;
f(x) > 0 para x > −3;
f(x) < 0 para x < −3.
43. a) Observa-se quê o gráfico representa uma função da forma T = at + b, em quê T é a tempera-túra em°C e t, o tempo em minuto.
Assim, considerando os pontos (0, −10) e (5, 30) quê pertencem à função, pode-se construir o sistema a seguir:
Da primeira equação, obtém-se b = −10. Substituindo o valor de b na segunda equação, obtém-se a = 8.
Portanto, a função é T = 8t − 10.
Para descobrir o tempo em quê a tempera-túra atingiu 0°C, basta considerar T = 0, assim:
8t − 10 = 0 ⇒ t = 1,25
Tem-se quê:
1,25 min = 1 min + 0,25 min =
= 1 min + 0,25 ⋅ 60 s =
= 1 min + 15 s = 1min15s
Portanto, a tempera-túra atingiu 0°C após 1 minuto e 15 segundos.
b) Como t = 1,25 é o zero da função, observando o gráfico, obtêm-se:
A tempera-túra é positiva para 1,25 < t ≤ 5.
A tempera-túra é negativa para 0 ≤ t < 1,25.
44.
a) Para expressar o peso mínimo P, quê a pessoa poderá atingir após n semanas, deve-se considerar quê a ela vai emagrecer o mássimo por semana, isto é, 2,5 kg. Desse modo, uma função quê relacione o peso com o número de semanas nesse spa é dada por P = 156 − 2,5n.
b) A princípio, deve-se descobrir quantas semanas são necessárias para essa pessoa chegar a 120 kg, ou seja, P = 120. Logo:
156 − 2,5n = 120 ⇒ n = 14,4
Como essa pessoa deve chegar a menos de 120 kg, então ela precisa ficar mais de 14,4 semanas. Como o número de semanas é um número natural, é razoável concluir quê ela deverá permanecer no mínimo 15 semanas para atingir seu objetivo.
45. a) 5x − 2(x + 2) ≥ 1 − (3 − 4x) ⇒
⇒ 5x − 2x − 4 ≥ 1 − 3 + 4x ⇒
⇒ x ≤ −2
S = {x ∈ ℝ | x ≤ −2}
b) ⇒
⇒ ![]() ⇒
⇒
⇒ 6x + 6 − x + 1 ≤ 2 ⇒
⇒ 5x ≤ −5 ⇒ x ≤ −1
S = {x ∈ ℝ | x ≤ −1}
46. Resolvendo a inequação, temos:
7x − 8 < 4x + 1 ⇒ 7x − 4x < 1 + 8 ⇒
⇒ 3x < 9 ⇒ x < 3
Como x é um número natural, os possíveis valores são 0, 1 e 2.
S = {0, 1, 2}
47. a) A área de um retângulo é calculada pelo produto entre dois de seus lados adjacentes. Para quê a área do retângulo seja maior do quê 50 cm2, deve-se calcular:
Área do retângulo: A = 10x cm2
A > 50 cm2 ⇒ 10x > 50 ⇒ x > 5
b) O perímetro de um polígono é calculado pela soma de todos seus lados. Portanto, o perímetro do retângulo póde sêr calculado por P = 20 + 2x. Como o perímetro deve sêr igual ou maior do quê 32 cm, então: P ≥ 32 ⇒ 20 + 2x ≥ 32 ⇒ x ≥ 6
48. a) Segundo o enunciado, obtêm-se as informações a seguir: Área do trapézio:
A1 = ⇒ A1 = 6x + 120
Área do retângulo: A2 = 12x
Considerando quê A1 > 2 ⋅ A2, tem-se: A1 > 2A2 ⇒ 6x + 120 > 2 ⋅ 12x ⇒
⇒ 6x + 120 > 24x ⇒ x < 6,66...
Portanto, o maior valor inteiro de x é 6.
b) Ao montar a equação, conforme o item anterior, porém em vez de colocar 12 (altura do triângulo e trapézio) substituir por MR. Logo:![]() ⇒
⇒
⇒ > 2x ⇒ x <
Como = 6,66..., então obteve-se a mesma resposta do item anterior, portanto não é necessária a medida MR para resolver a atividade.
49. a) Para obtêr a função quê representa o lucro da empresa A, deve-se considerar os pontos quê estão no qüadro e montar o sistema a seguir:
LA :(50, 0) e (0, −500)
Da segunda equação, obtém-se b = −500, e substituindo esse valor na primeira equação, obtém-se a = 10.
Logo: LA (x) = 10x − 500, para x ≥ 0.
b) Para descobrir os valores para quê o lucro de B seja maior do quê A, deve-se, primeiro, encontrar a lei de formação de LB. Assim, utilizando os pontos fornecidos pelo enunciado (60, 0) e (0, −1.000), pode-se construir o seguinte sistema:
Da segunda equação, obtém-se b = −1.000, e substituindo esse valor na primeira equação, obtém-se a = . Logo:
LB (x) = x − 1.000, para x ≥ 0.
Como LB (x) > LA (x), então:
x − 1.000 > 10x − 500
50x − 3.000 > 30x − 1.500
x > 75
Portanto, para x > 75, o LB é superior a LA.
Atividades complementares
1. Seja p(t) o valor monetário do equipamento no tempo t dado em anos. Devido ao decrescimento linear, temos p(t) = a ⋅ t + b, com a ≠ 0. Considerando o tempo atual como t = 0 e três anos atrás como t = −3, temos os pontos (−3, 180.000) e (0, 135.000). Logo,
Da segunda equação, obtém-se b = 135.000 e, substituindo esse valor na primeira equação, obtém-se:
−3a = 180.000 − 135.000 ⇒ a = −15.000
Então, a lei de formação da função p é p(t) = −15.000 ⋅ t + 135.000. Assim, calculando o valor monetário da máquina daqui a dois anos, basta substituirmos t = 2 em p(t): p(2) = −15.000 ⋅ 2 + 135.000 = 105.000
Resposta: alternativa a.
2. De acôr-do com o texto, a substância A já estava presente no organismo. O medicamento aumentou a quantidade da substância por um período de tempo e depois voltou ao normal. Sendo assim, deve-se desconsiderar as alternativas a e b, pois, em ambos os casos, inicialmente já havia uma quantidade da substância A no corpo; porém, depois de um tempo, a quantidade não voltou ao normal, ficou acima da quantidade inicial.
Não se deve considerar a alternativa c, pois o gráfico mostra quê inicialmente a quantidade da substância A era nula, o quê contraria o enunciado.
Também se deve desconsiderar a alternativa e, pois o gráfico mostra quê, depois de um tempo, a quantidade da substância A diminuiu, e o texto afirma quê aumentou.
Resposta: alternativa d.
Página trezentos e setenta e oito
3. Analisando as sentenças, segundo as informações obtidas no gráfico, conclui-se quê:
a) Falsa. No intervalo entre t = 10 e t = 20, as tempera-túras são decrescentes.
b) Falsa, pois, no intervalo entre t = 5 e t = 10, as tempera-túras são crescentes.
c) Verdadeira. A partir de t = 20, quanto maior o tempo, maior é a tempera-túra.
d) Falsa, pois para t = 20 a tempera-túra é inferior a 50.
e) Falsa. Identifica-se no gráfico quê um determinado valor de tempera-túra póde sêr obtído em, no mássimo, 3 instantes diferentes.
Resposta: alternativa c.
4. A reta r é o gráfico de uma função afim f dada por f(x) = a ⋅ x + b, com a e b sêndo números reais e a ≠ 0.
A reta r corta o eixo das ordenadas em (0,−4), o quê implica quê b = −4.
Para descobrir o valor de a, utilizamos o ponto (4,6):
f(4) = 6 ⇒ 4a − 4 = 6 ⇒ a =
Assim, f(x) = x − 4. Agora, note quê a abscissa do ponto P é o zero da função afim f e, portanto, P é da forma . Assim, o valor da abscissa do ponto P é:
Resposta: alternativa d.
5. Como o salário fixo é de R$ 300,00, deve-se calcular a comissão de cada mês.
No 1º mês foram vendidos 500 m de tecido com 1,40 m de largura. A área do tecido foi A = 500 ⋅ 1,4 = 700.
Então, o vendedor receberia de comissão:
700 ⋅ 0,5 = 350, portanto R$ 350,00. E seu salário final seria: 300 + 350 = 650, portanto R$ 650,00.
2º mês: Como, no segundo mês, supõe-se vender o dôbro, a comissão também será dobrada, ou seja, R$ 700,00. Então, o salário seria de 300 + 700 = 1.000, portanto R$ 1.000,00.
Resposta: alternativa c.
6. Observando o gráfico, pode-se notar quê, ao aumentar 10 métros de fio (de 15 para 25), o valor aumentou R$ 20,00 (de R$ 80,00 para R$ 100,00), ou seja, o Sr. Luiz cobra R$ 2,00 por metro instalado de fio.
Assim, como ele cobrou R$ 80,00 para instalar 15 metros de fio, pode-se concluir quê o valor fixo cobrado é de: 80 − 2 ⋅ 15 = 50, portanto R$ 50,00. Assim, a lei da função quê fornece o valor cobrado pelo Sr. Luiz é: fL (x) = 2x + 50. Portanto, pode-se descartar as alternativas a e b.
Já o Sr. José cobra R$ 4,50 por métro e não cobra um valor fixo, ou seja, a lei de formação da função é: fJ (x) = 4,5x. Se alguém contratar um serviço quê utilize 30 metros de fio, o orçamento do Sr. José (R$ 135,00) será maior do quê o orçamento do Sr. Luiz (R$ 110,00). Portanto, a alternativa c está incorréta. Igualando as duas funções, para saber a metragem em quê o valor a sêr cobrado será equivalente, tem-se:
2x + 50 = 4,5x ⇒ 2,5x = 50 ⇒ x = 20. Portanto, se a instalação for de 20 m, não haverá diferença no valor cobrado pêlos dois.
Resposta: alternativa d.
7. Para a função sêr crescente, deve-se ter 3 − 2a > 0. Logo:
3 − 2a > 0 ⇒ −2a > −3 ⇒ 2a < 3 ⇒
⇒ a <
Resposta: alternativa b.
8. A semirreta representa o gráfico de uma função f dada por f(x) = a ⋅ x + b, com a e b números reais e a ≠ 0. De acôr-do com o gráfico, a taxa fixa é R$ 17,00, já quê o gráfico passa pelo ponto (0, 17). Ou seja, f(x) = a ⋅ x + 17. Para encontrarmos o valor de a, vamos utilizar o ponto (7; 42,20):
f(7) = 42,20 ⇒ 7a + 17 = 42,20 ⇒ a = 3,6 Assim, f(x) = 3,6 ⋅ x + 17. Agora, sabendo quê o consumo do mês de dezembro foi o dôbro do consumo do mês de novembro, então devemos calcular o valor de f em x = 2 ⋅ 7 = 14. Ao fazer isso, obtemos f(14) = 3,6 ⋅ 14 + 17 = 67,4.
Portanto, o valor da fatura no mês de dezembro dessa residência foi R$ 67,40. Resposta: alternativa a.
9. Para os reservatórios estarem com o mesmo volume, deve-se ter a condição
VA (t) = VB (t).
Logo:
VA (t) = VB (t) ⇒ 200 + 3t = 5.000 − 3t ⇒
⇒ 6t = 4.800 ⇒ t = 800
Portanto, os reservatórios terão o mesmo volume em 800 minutos.
Resposta: alternativa d.
10. De acôr-do com as informações sobre as funções f(x) = 2x + 3 e g(x) = −x + 6, temos:
a) Falsa. As funções f e g não possuem pontos de mássimo ou mínimos, já quê ambas são não constantes e possuem domínio igual a D(f) = D(g) = ℝ.
b) Falsa. A função f é crescente, pois seu coeficiente angular é igual a 2 > 0. Já a função g é decrescente, pois seu coeficiente angular é igual a −1 < 0.
c) Falsa. As funções f e g têm o mesmo domínio: D(f) = D(g) = ℝ.
d) Verdadeira. Calculando f e g no ponto x = 1, temos:
Portanto, o ponto (1, 5) é comum as funções f e g.
e) Falsa. De acôr-do com o item d, as funções f e g se intersectam no ponto (1, 5).
Resposta: alternativa d.
Capítulo 4 • Função quadrática
Atividades
1. Considerando a função f(x) = x2 − 5x + 4 e calculando o valor numérico para cada item, tem-se:
a) f(0) = 02 − 5 ⋅ 0 + 4 = 4
b) f(−4) = (−4)2 − 5 ⋅ (−4) + 4 = 40
c) f() = ()2 - 5 ⋅ () + 4 =
d) = − 5 ⋅ + 4 =
= 6 −
2. Como a altura h está em função do tempo t, a altura do objeto após 3 segundos do lançamento é:
h(t) = 30t − 5t2 ⇒
⇒ h(3) = 30 ⋅ 3 − 5(3)2 = 45
O objeto, depois de 3 segundos do lançamento, estará a 45 metros do solo.
3. Considerando a fórmula proposta no enunciado, pode-se substituir n por 50, assim:
S(50) = S(5) = +
S(50) = + 25
S(50) = 1.275
4. a) Pelo enunciado, a produção é vendida por (500 − x) reais a unidade, e cada unidade tem um custo de R$ 100,00. Também se deve considerar quê há uma despesa fixa mensal de R$ 10.000,00.
Assim, pode-se concluir quê a receita R(x), em função das unidades vendidas, póde sêr calculada por:
R(x) = (500 − x)x ⇒
⇒ R(x) = −x2 + 500x
E a função custo C é:
C(x) = 100x + 10.000
Como o lucro é representado pela diferença entre receita e custo, tem-se:
L(x) = R(x) − C(x) ⇒ L(x) =
= −x2 + 500x − (100x + 10.000) ⇒
⇒ L(x) = −x2 + 400x − 10.000
b) O lucro para 100 produtos póde sêr calculado considerando x = 100, ou seja:
L(100) = −(100)2 +
+ 400 ⋅ (100) − 10.000 = 20.000
Portanto, o lucro será de R$ 20.000,00.
5. Como a função f é quadrática, então pode-se escrevê-la na forma f(x) = ax2 + bx + c; considerando os dados do problema, f(0) = 6, f(1) = 2 e f(−2) = 20, tem-se:
6 = a ⋅ (0)2 + b ⋅ (0) + c ⇒ c = 6
2 = a ⋅ (1)2 + b ⋅ (1) + c ⇒
⇒ a + b = −4
20 = a ⋅ (−2)2 + b ⋅ (−2) + c ⇒
⇒ 4a − 2b = 14
Página trezentos e setenta e nove
Portanto, obtém-se c = 6 e resolve-se o sistema a seguir envolvendo os coeficientes a e b.
Simplificando a segunda equação por 2 e, em seguida, adicionando ambas as equações, obtém-se a = 1. Substituindo o valor de a em qualquer uma das equações, obtém-se b = −5.
Logo, f(x) = x2 − 5x + 6.
Calculando f :
f
6. Para traçar uma parábola, deve-se atribuir alguns valores para x e calcular o respectivo valor numérico, ou seja, o valor de y. Esse par (x, y) será um ponto da parábola.
a) y = −x2
x |
y |
|---|---|
−2 |
−4 |
−1 |
−1 |
0 |
0 |
1 |
−1 |
2 |
−4 |
Portanto, o esboço da parábola será:
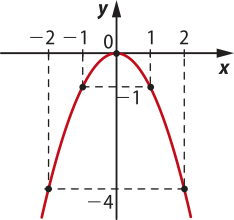
b) y = x2 − 4
x |
y |
|---|---|
−2 |
0 |
0 |
−4 |
2 |
0 |
Portanto, o esboço da parábola será:
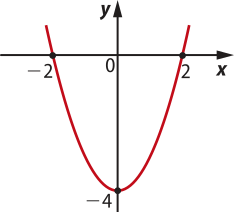
c) y = −x2 + 6x − 9
x |
y |
|---|---|
1 |
−4 |
2 |
−1 |
3 |
0 |
4 |
−1 |
Portanto, o esboço da parábola será:
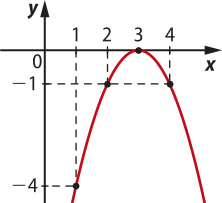
d) y = x2 − 5x
x |
y |
|---|---|
−1 |
6 |
0 |
0 |
5 |
0 |
Portanto, o esboço da parábola será:
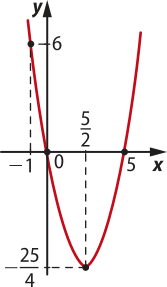
7. Como o ponto (1, 6) deve pertencer à parábola, então pode-se concluir quê, quando x = 1, obrigatória mente y = 6.
Considerando essa informação, tem-se:
y = 3x2 − x + m ⇒
⇒ 6 = 3(1)2 − 1 + m ⇒
⇒ 6 = 3 − 1 + m ⇒ m = 4
8. Observando quê os pontos A e D tem a mesma ordenada, então D é da forma D(x, 5). Para determinar a abscissa de D, vamos avaliar os pontos A(0, 5) e C(5, 0) na função f(x) = x2 − bx + c:
Assim, f(x) = x2 − 6x + 5. Agora, avaliando f no ponto D(x, 5) e notando quê x > 0, obtemos:
f(x) = x2 − 6x + 5 = 5 ⇒ x2 − 6x = 0 ⇒
⇒ x ⋅ (x − 6) = 0 ⇒ x = 6
Logo, as coordenadas do ponto D são (6, 5).
Resposta: alternativa d.
9. Para encontrar as coordenadas dos vértices utilizam-se as fórmulas xv = e yv = . Já para saber se a função possui zeros, primeiro calcula-se o valor do ∆ para a equação y = 0 e, se for positivo, encontram-se as raízes. Ver esse processo em cada item a seguir.
a) y = x2 − 6x + 5
Considerando x2 − 6x + 5 = 0, temos:
(delta)" = (−6)2 − 4 ⋅ 1 ⋅ (5) = 16
Assim:
x =
Logo, os zeros da função são x(minutos)" = 1 e x(segundos)" = 5.
b) y = 3x2 − 4x
Considerando 3x2 − 4x = 0, temos:
(delta)" = (−4)2 − 4 ⋅ 3 ⋅ 0 = 16
Assim:
x =
Logo, os zeros da função são x(minutos)" = 0 e x(segundos)" = .
c) y = −x2 + x − 3
Considerando −x2 + x − 3 = 0, temos:
(delta)" = (1)2 − 4 ⋅ (−1) ⋅ (−3) = −11
A função não tem zeros.
d) y = x2 − 9
Considerando x2 − 9 = 0, temos:
(delta)" = (0)2 − 4 ⋅ 1 ⋅ (−9) = 36
Assim:
x =
Logo, os zeros da função são x(minutos)" = −3 e x(segundos)" = 3.
e) y = −6x2
Considerando −6x2 = 0, temos:
(delta)" = (0)2 − 4 ⋅ (−6) ⋅ 0 = 0
Assim:
x =
Logo, o zero da função é x(minutos)" = x(segundos)" = 0.
f) y = 4x2 − x +
Considerando 4x2 − x + = 0, temos:
(delta)" = (−1)2 − 4 ⋅ (4) ⋅ =
Sendo assim, a função não tem zeros.
10. Como 2 é um zero da função, pode-se escrever:
k(2)2 − 2(2) + 3 = 0 ⇒
⇒ 4k − 1 = 0 ⇒ k =
11. O produto das raízes póde sêr calculado por . Como o enunciado forneceu quê as raízes são −2 e 5, tem-se:
−2 ⋅ 5 = ⇒ a = −1
Já a soma das raízes póde sêr calculada por . Como a = −1, tem-se:
−2 + 5 = ⇒ b = 3
Portanto, a função é f(x) = −x2 + 3x + 10. Como já se sabe quais são os zeros da função, para se traçar um esboço da função, precisam-se calcular as coordenadas do vértice.
Calculando as coordenadas do vértice:
(delta)" = (3)2 − 4 ⋅ (−1) ⋅ (10) = 49
xv = ⇒ xv = =
yv = ⇒ yv = =
Página trezentos e oitenta
Portanto, V .
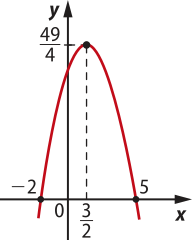
12. a) Para a função ter um zero apenas, necessariamente é preciso quê:
(delta)" = 0 ⇒ (2m)2 − 4 ⋅ 1 ⋅ 16 = 0 ⇒
⇒ 4m2 − 64 = 0 ⇒ m2 = 16 ⇒ m = ±4
b) Como o gráfico deve passar pelo ponto (2, −4), então f(2) = −4. Logo:
−4 = (2)2 + 2(m)(2) + 16 ⇒ m = −6
13. a) Para a função f(x) = x2 − 2x + k ter dois zeros, é necessário quê (delta)" > 0.
Portanto:
(delta)" > 0 ⇒ b2 − 4ac > 0 ⇒
⇒ (−2)2 − 4 ⋅ 1 ⋅ k > 0 ⇒
⇒ −4k > −4 ⇒ k < 1
b) Para a função ter apenas um zero, é necessário quê (delta)" = 0. Portanto:
(delta)" = 0 ⇒ (−2)2 − 4 ⋅ 1 ⋅ k = 0 ⇒
⇒ −4k = −4 ⇒ k = 1
c) Para a função não ter zeros, é necessário quê (delta)" < 0. Portanto:
(delta)" < 0 ⇒ (−2)2 − 4 ⋅ 1 ⋅ k < 0 ⇒
⇒ −4k < −4 ⇒ k > 1
14. Como o volume do reservatório é de 72 m3 e a função quê representa a drenagem em relação ao tempo é V(t) = 24t − 2t2, considera-se quê estará vazio quanto V(t) = 72. Portanto:
24t − 2t2 = 72 ⇒ − 2t2 + 24t − 72 = 0 ⇒
⇒ t2 − 12t + 36 = 0
Resolvendo a equação:
(delta)" = (−12)2 − 4 ⋅ (1) ⋅ (36) = 0
Assim:
t = = = 6
Ou seja, foram necessárias 6 horas para quê o reservatório se esvaziasse completamente. Como o processo de drenagem iniciou-se às 10 horas, o reservatório ficou completamente vazio às 16 horas, pois 10 + 6 = 16.
Resposta: alternativa b.
15. a) A função f é a quê tem como gráfico uma parábola. Portanto, os pontos de intersecção com o eixo das abscissas são da forma (x, 0), em quê x é raiz de f. Logo:
f(x) = (x + 1)(x − 3) ⇒
⇒ (x + 1)(x − 3) = 0
Como essa é uma equação produto, tem-se quê:
(x + 1) = 0 ou (x − 3) = 0
Logo, x = −1 ou x = 3.
Portanto, os pontos de intersecção são (−1, 0) e (3, 0).
b) Pode-se identificar o ponto de intersecção com o eixo das ordenadas considerando x = 0. Logo:
f(0) = (0 + 1)(0 − 3) = 1 ⋅ (−3) = −3
O ponto de intersecção com o eixo das ordenadas é (0, −3).
c) O ponto de intersecção da reta com o eixo das ordenadas ocorre quando x = 0. Logo:
g(0) = + 3 = 3
O ponto de intersecção da reta com o eixo das ordenadas é (0, 3).
d) Para calcular o ponto de intersecção entre as duas funções, deve-se considerar f(x) = g(x). Logo:
x2 − 2x − 3 = + 3
2x2 − 5x − 12 = 0
Resolvendo a equação:
(delta)" = (−5)2 − 4 ⋅ (2) ⋅ (−12) = 121
Assim: x = =
Portanto, x’ = 4 e x” = .
Como se deseja apenas a intersecção do segundo quadrante, deve-se desconsiderar o valor positivo de x. Escolhendo a função g, o respectivo valor numérico para x = é:
g = + 3 ⇒
⇒ g =
Portanto, o ponto de intersecção entre as funções f e g é .
16. a) Segundo o enunciado da atividade, pode-se considerar quê v = 40, portanto:
d(v)= (v2 + 8v)⇒
⇒ d(40)= (402 + 8 ⋅ 40) = 16
Portanto, se o carro estiver a 40 km/h, a distância de frenagem será de 16 m.
b) Como a distância de frenagem é 53,2 m, então pode-se concluir quê d(v) = 53,2. Logo:
53,2 = (v2 + 8v)⇒
⇒ v2 + 8v − 6.384 = 0
Resolvendo a equação:
(delta)" = (8)2 − 4 ⋅ 1 ⋅ (−6.384) = 25.600
Assim:
v = =
Logo, v(minutos)" = −84 e v(segundos)" = 76.
Nesse caso, deve-se desconsiderar a resposta negativa.
Portanto, a velocidade é 76 km/h.
17. Pode-se admitir, nesse caso, quê os zeros da função são os momentos em quê a bola está no chão, ou seja, no primeiro momento, quando a bola é chutada, portanto, quando x = 0. O segundo momento ocorre após a cobrança da falta, exatamente quando a bola toca no chão novamente. Portanto, a distância entre o ponto quê a bola sai do solo na primeira vez e quando ela repousa no solo novamente se dá pela diferença entre os zeros da função. Como a trajetória é uma parábola, a maior altura quê a bola vai alcançar se dá no yV.
a) Calculando os zeros da função: h(x)= +0,5x = 0, tem-se:
(delta)" = (0,5)2 − 4 ⋅ ⋅ (0) = 0,25
Assim:
Logo, os zeros da função são x(minutos)" = 0 e x(segundos)" = 30.
Portanto, a distância em quê a bola sai do solo e quê chega novamente ao solo é dada por 30 − 0 = 30, ou seja, 30 metros.
b) Como a altura mássima equivale a yV, tem-se:
yv =
⇒ yv = = 3,75
A altura mássima quê a bola alcança é 3,75 metros.
18. Para cada item, deve-se encontrar, quando houver, o(s) zero(s) da função fazendo y = 0, em seguida as coordenadas do vértice e, também, do ponto de intersecção da parábola com o eixo y. Utilizando esses pontos, pode-se esboçar a parábola.
a) y = x2 − 5x + 6
Considerando x2 − 5x + 6 = 0, temos:
(delta)" = (−5)2 − 4 ⋅ (1) ⋅ (6) = 1
Assim: x = =
Logo, os zeros da função são x(minutos)" = 2 e x(segundos)" = 3.
Calculando o vértice da parábola:
xv = ⇒ xv = =
yv = ⇒ yv = =
Portanto, V .
A parábola intersecta o eixo y no ponto de coordenada (0, c), ou seja, (0, 6).
Traçando o gráfico:
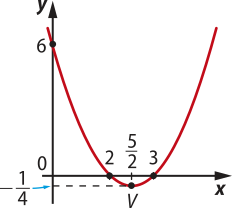
b) y = −x2 + 4
Considerando −x2 + 4 = 0, temos:
(delta)" = (0)2 − 4 ⋅ (−1) ⋅ (4) = 16
Assim: x = =
Logo, os zeros da função são x(minutos)" = −2 e x(segundos)" = 2.
Calculando o vértice da parábola:
xv = ⇒xv = = 0
yv = ⇒ yv = = 4
Portanto, V(0, 4).
Página trezentos e oitenta e um
A parábola intersecta o eixo y no ponto de coordenada (0, c), ou seja, (0, 4).
Traçando o gráfico:
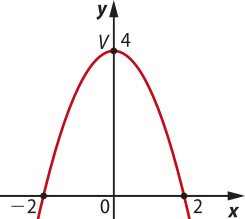
c) y = x2 − 4x + 4
Considerando x2 − 4x + 4 = 0, temos: (delta)" = (−4)2 − 4 ⋅ (1) ⋅ (4) = 0
Assim: x = = = 2
Logo, o zero da função é x = 2.
Calculando o vértice da parábola:
xv = ⇒ xv = = 2
yv = ⇒ yv = = 0
Portanto, V(2, 0).
A parábola intersecta o eixo y no ponto de coordenada (0, c), ou seja, (0, 4).
Traçando o gráfico:
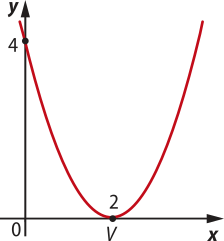
d) y = x2 + 2x + 5
Considerando x2 + 2x + 5 = 0, temos:
(delta)" = (2)2 − 4 ⋅ (1) ⋅ (5) = −16
Sendo assim, a função não possui zeros.
Calculando o vértice da parábola:
xv = ⇒xv = = −1
yv = ⇒yv = = 4
Portanto, V(−1, 4).
Para x = −2, temos:
y = (−2)2 + 2(−2) + 5 = 5
Para x = 0, temos:
y = 02 + 2 ⋅ 0 + 5 = 5
Portanto, o gráfico passa pelo ponto (−2, 5) e cruza o eixo y no ponto (0, 5).
Traçando o gráfico, tem-se:
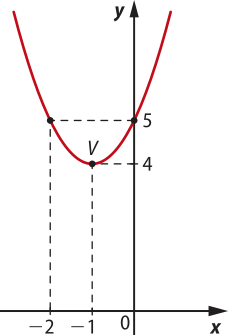
19. Para determinar a imagem de uma função quadrática, é necessário calcular a ordenada do vértice. Assim, em cada situação, tem-se:
a) f(x) = 3x2 − 2x − 1
(delta)" = (−2)2 − 4 ⋅ (3) ⋅ (−1) = 16
yV = =
Como a concavidade da parábola é voltada para cima, pois a > 0, tem-se Im(f)= .
b) g(x) = −2x2 + 1
(delta)" = (0)2 − 4 ⋅ (−2) ⋅ (1) = 8
yV = = 1
Como a concavidade da parábola é voltada para baixo, pois a < 0, tem-se Im(g) = {y ∈ ℝ | y ≤ 1}.
20. Segundo o enunciado, a área do cercado é retangular, por isso seus lados opostos são congruentes. Considerando quê a medida do lado adjacente à parede é x, pode-se afirmar quê o lado paralelo à parede méde 40 − 2x, pois a cerca méde 40 m e foi completamente utilizada.
Como a área do retângulo, A(x), é o produto entre dois lados adjacentes, então:
A(x) = x(40 − 2x) ⇒ A(x) = 40x − 2x2
A área mássima é representada pela ordenada do vértice, ou seja, yV.
Assim, (delta)" = (40)2 − 4 ⋅ (−2) ⋅ (0) = 1.600
yV = = 200
A área mássima será 200 m2.
21. Segundo o enunciado, sabe-se quê:
AABCD = 30 ⋅ 50 = 1.500 cm2.
Considerando a área dos triângulos
AAMN, ACPQ, AMDQ e ANBP, tem-se:
AAMN = ACPQ =
AMDQ = ANBP
=
= =
Segundo a imagem no enunciado, pode-se afirmar quê:
AMNPQ = AABCD − 2 ⋅ (AAMN + AMDQ)
Assim:
AMNPQ =
= 1.500 − 2 =
= 1.500 − x2 − 1.500 + 80x − x2 =
= −2x2 + 80x
Portanto, o valor da área AMNPQ depende do valor de x por uma função da forma:
A(x) = −2x2 + 80x.
Como o coeficiente de x2 é negativo, a parábola terá a concavidade voltada para baixo e a ordenada do vértice será o valor mássimo. Esse valor é obtído quando a abscissa dêêsse ponto for:
xV = = = 20
Portanto, o quadrilátero terá área mássima quando x = 20 cm.
22. A variação de tempera-túra de uma peça, em relação ao tempo, é descrita pela função f(t) = −t2 + 4t + 2, com 0 < t < 5.
Como a parábola tem concavidade para baixo, a abscissa xv representa o momento em quê a função atinge o valor mássimo, então:
xv = = 2;
Portanto, a tempera-túra atingirá o valor mássimo quando t = 2.
23. Considerando como x o valor da redução, em reais, tem-se: preêço do combo: 10 − x
Quantidade de combos vendida:
200 + 100x
Para cada real de desconto, são vendidos 100 combos a mais.
Portanto, a função quê representa a arrecadação, ou receita, é:
R(x) = (10 − x)(200 + 100x) ⇒
⇒ R(x) = −100x2 + 800x + 2.000
Assim, a mássima arrecadação é representada pelo yV.
Sendo assim:
(delta)" = (800)2 − 4 ⋅ (−100) ⋅ (2.000) =
= 1.440.000
yV = = 3.600
A arrecadação mássima será de R$ 3.600,00.
Resposta: alternativa c.
24. a) Do enunciado, obtêm-se as informações:
R(x) = L(x) + C(x), R(x) = x2 + 7.500x + + 3.000 e C(x) = 2x2 + 2.500x + 3.000
Portanto:
R(x) = L(x) + C(x) ⇒ L(x) = R(x) − C(x)
L(x) = x2 + 7.500x + 3.000 − (2x2 + 2.500x + 3.000)
L(x) = −x2 + 5.000x
Resolvendo a equação L = 0, obtém-se quê os zeros da função são 0 e 5.000.
Com relação ao vértice, tem-se:
xv = = 2.500
(delta)" = (5.000)2 − 4 ⋅ (−1) ⋅ (0) = 25.000.000
yv = = 6.250.000
Portanto, o esboço do gráfico é:
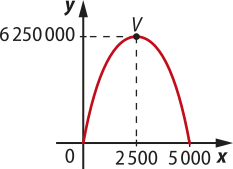
b) Conf orme o gráfico, o lucro mássimo é obtído para 2.500 unidades produzidas.
25. Sejam y1 e y2 as ordenadas dos pontos P e V, isto é, P(4, y1) e V(2, y2). Assim,
Agora, para calcular a reta quê passa por P(4, 3) e V(2, −1), devemos calcular o coeficiente angular da reta:
m = = 2
Página trezentos e oitenta e dois
Logo, a reta póde sêr expressa na forma g(x) = 2x + b, em quê b é um número real. Lembrando quê P(4, 3) pertence a reta, temos:
3 = g(4) = 2 ⋅ 4 + b ⇒ b = −5
Então, a reta quê passa pêlos pontos P e V intersecta o eixo y no ponto de ordenada igual a −5.
Resposta: alternativa e.
26. a) A função f(x) = x2 − 3x − 10, tem concavidade para cima, pois a = 1, ou seja, a > 0.
Considerando x2 − 3x − 10 = 0, temos:
(delta)" = (−3)2 − 4 ⋅ (1) ⋅ (−10) = 49
Assim:
x = =
Portanto, x’ = −2 e x” = 5.
Com base nesses dados, é possível fazer o seguinte esboço:

Portanto:
f(x) = 0 para x = −2 ou x = 5
f(x) > 0 para {x ∈ ℝ | x < −2 ou x > 5}
f(x) < 0 para {x ∈ ℝ | −2 < x < 5}
b) A função f(x) = −x2 + 2x, tem concavidade para baixo, pois a = −1, ou seja, a < 0.
Considerando −x2 + 2x = 0, temos:
(delta)" = (2)2 − 4 ⋅ (−1) ⋅ (0) = 4
Assim:
x = =
Portanto, x’ = 0 e x” = 2.
Com base nesses dados, é possível fazer o seguinte esboço:
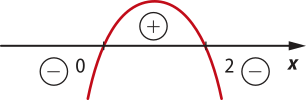
Portanto:
f(x) = 0 para x = 0 ou x = 2
f(x) > 0 para {x ∈ ℝ | 0 < x < 2}
f(x) < 0 para {x ∈ ℝ | x < 0 ou x > 2}
c) A função f(x) = −4x2 + 4x − 1 tem concavidade para baixo, pois a = −4, ou seja, a < 0.
Considerando −4x2 + 4x − 1 = 0, temos:
(delta)" = (4)2 − 4 ⋅ (−4) ⋅ (−1) = 0
Assim:
x = = =
Portanto, x = .
Com base nesses dados, é possível fazer o seguinte esboço:
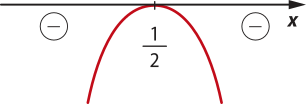
Portanto:
f(x) = 0 para x = .
f(x) < 0 para .
d) A função f(x) = x2 − x + 10, tem concavidade para cima, pois a = 1, ou seja, a > 0.
Considerando x2 − x + 10 = 0, temos:
(delta)" = (−1)2 − 4 ⋅ (1) ⋅ (10) = −39
Como (delta)" < 0 a função não possui zeros, ou seja, ela não possui intersecções com o eixo das abscissas. Portanto, como a > 0, a parábola está acima do eixo x.
Com base nesses dados, é possível fazer o seguinte esboço:

Portanto:
f(x) > 0 para todo x real.
27. Para a função sêr positiva para todo x real, necessariamente, deve-se ter a > 0 e (delta)" < 0. Como a = 1, deve-se satisfazer a segunda condição. Como f(x) = x2 − (2m + 1)x + m2, então:
(delta)" < 0 ⇒ (2m + 1)2 − 4(1)(m2) < 0 ⇒
⇒ 4m < −1 ⇒m <
S =
28. Para a função sêr negativa, para todo x real, necessariamente, deve-se ter a < 0 e (delta)" < 0.
Para a < 0, tem-se k < 0.
Para (delta)" < 0, tem-se 4k2 − 4(k)(k − 1) < 0 ⇒
⇒ 4k < 0 ⇒ k < 0.
Como ambas as situações apresentam a mesma solução, então k < 0.
S = {k ∈ ℝ | k < 0}
29. a) Dada a equação x2 − 2x − 8 = 0, tem-se:
(delta)" = (−2)2 − 4 ⋅ (1) ⋅ (−8) = 36
Logo:
x = =
Portanto, x’= −2 e x” = 4.
Como a = 1, logo a > 0, então a concavidade da parábola é voltada para cima. Com essas informações, pode-se fazer o seguinte esboço:

Como a solução considera apenas os valores negativos, então S =
= {x ∈ ℝ | −2 < x < 4}.
b) Dada a equação 9x2 − 8x − 1 = 0, tem-se:
(delta)" = (−8)2 − 4 ⋅ (9) ⋅ (−1) = 100
Logo:
x = =
Portanto, x’ = e x” = 1.
Como a = 9, logo a > 0, então a concavidade da parábola é voltada para cima. Assim, com essas informações, pode-se fazer o seguinte esboço:
![]()
Como a solução considera apenas os valores maiores ou iguais a zero, então
S = .
c) Dada a equação −3x2 + 2x − 1 = 0, tem-se:
(delta)" = (2)2 − 4 ⋅ (−3) ⋅ (−1) = −8
Assim, a equação não possui solução real.
Como a = −3, logo a < 0, então a concavidade da parábola é voltada para baixo. Com essas informações, pode-se fazer o seguinte esboço:
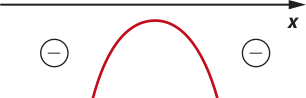
Como a solução considera apenas os valores maiores do quê zero, então S = ∅.
d) Dada a equação −x2 + 4x − 4 = 0, tem-se:
(delta)" = (4)2 − 4 ⋅ (−1) ⋅ (−4) = 0
Logo:
x = = = 2
Portanto, x = 2.
Como a = −1, logo a < 0, então a concavidade da parábola é voltada para baixo. Com essas informações, pode-se fazer o seguinte esboço:
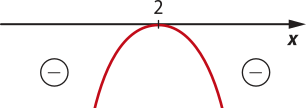
Como a solução considera apenas os valores menóres do quê zero, então
S = {x ∈ ℝ | x ≠ 2}.
30. Aplicando a propriedade distributiva em ambos os lados da inequação (2x − 5)(x − 4) − 7 ≥ (x − 2)(x − 3) e associando os termos semelhantes, chega-se à inequação x2 − 8x + 7 ≥ 0.
Considerando x2 − 8x + 7 = 0, temos:
(delta)" = (−8)2 − 4 ⋅ (1) ⋅ (7) = 36
Logo:
x = =
Portanto, x’ = 1 e x” = 7.
Como a = 1, logo a > 0, então a concavidade da parábola é voltada para cima. Com essas informações, pode-se fazer o seguinte esboço:

Portanto, a solução é S = {x ∈ ℝ | x ≤ 1 ou x ≥ 7}.
Página trezentos e oitenta e três
31. Como f(x) = x2 − 3x + 8, então, f(1) =
= 12 − 3(1) + 8 = 6.
Como se deve encontrar o conjunto solução para f(x) ≥ 2f(1), logo:
x2 − 3x + 8 ≥ 2 ⋅ 6 ⇒ x2 − 3x − 4 ≥ 0
Considerando x2 − 3x − 4 = 0, temos:
(delta)" = (−3)2 − 4 ⋅ (1) ⋅ (−4) = 25
Assim:
x = =
Portanto, x’ = −1 e x” = 4.
Como a = 1, logo a > 0, então a concavidade da parábola é voltada para cima. Com essas informações, pode-se fazer o seguinte esboço:

Portanto, o conjunto solução será S =
= {x ∈ ℝ | x ≤ −1 ou x ≥ 4}
32. a) Calcular o conjunto solução para h(t) ≥ 8 equivale a:
−5t2 + 7t + 6 ≥ 8 ⇒ −5t2 + 7t − 2 ≥ 0
Considerando −5t2 + 7t − 2 = 0, temos:
(delta)" = (7)2 − 4 ⋅ (−5) ⋅ (−2) = 9
Logo:
t = =
Assim, t’ = e t” = 1.
Como a = −5, logo a < 0, então a concavidade da parábola é voltada para baixo. Portanto, com essas informações, pode-se fazer o seguinte esboço:

Portanto, o conjunto solução é S =
= .
b) Para determinar o conjunto imagem da função h(t) = −5t2 + 7t + 6, determinamos inicialmente a ordenada yv do vértice da parábola. Sendo assim:
yv = = = 8,45
Como a < 0, o gráfico de h tem concavidade voltada para baixo e yv é o valor mássimo da função.
Portanto, a imagem da função h é Im(h) = {y ∈ ℝ | y ≤ 8,45} ou ]−∞, 8,45].
33. a) Como a função L = −x2 + 30x − 5 representa o lucro de uma empresa em relação à quantidade mensal de vendas, o maior lucro obtído é representado pelo vértice da parábola quê representa essa situação, ou seja:
Lmáx = L(xv) ou Lmáx = yv. Logo:
xv = = 15
Lmáx = −(15)2 + 30 ⋅ 15 − 5 ⇒
⇒ Lmáx = 220
Assim, o lucro mensal mássimo é de R$ 220,00.
b) Considerar quê o lucro mensal, no mínimo, deve sêr 195 equivale a dizêr quê:
−x2 + 30x − 5 ≥ 195 ⇒
⇒ −x2 + 30x − 200 ≥ 0
Considerando −x2 + 30x − 200 = 0, temos:
(delta)" = (30)2 − 4 ⋅ (−1) ⋅ (−200) = 100
Logo:
x = =
Portanto, x’ = 10 e x” = 20.
Como a = −1, logo a < 0, então a concavidade da parábola é voltada para baixo. Portanto, com essas informações, pode-se fazer o seguinte esboço:

Portanto, o valor de x deve variar segundo o conjunto
S = {x ∈ ℝ | 10 ≤ x ≤ 20}.
34. a) Para quê haja lucro, os valores de venda devem sêr maiores do quê o custo, ou seja, V > C. Logo:
−5n2 + 100n − 320 > 5 + 10n − n2 + 18n − 65 > 0
Considerando −n2 + 18n − 65 = 0, temos:
(delta)" = (18)2 − 4 ⋅ (−1) ⋅ (−65) = 64
Logo:
n = =
Portanto, n’ = 5 e n” = 13.
Como a = −1, logo a < 0, então a concavidade da parábola é voltada para baixo. Portanto, com essas informações, pode-se fazer o seguinte esboço:
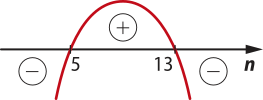
Para quê haja lucro nas vendas, deve-se ter: 5 < n < 13, sêndo n um número inteiro.
b) Como o lucro (L) é a diferença entre receita (V) e custo (C), tem-se:
L = V − C
L = −5n2 + 100n − 320 − (5 + 10n)
L = −5n2 + 90n − 325
O valor de n quê acarreta o maior lucro possível ocorre no vértice da função, ou seja:
xv = = 9
(delta)" = (90)2 − 4 ⋅ (−5) ⋅ (−325) = 1.600
yV = = 80
Portanto, o maior lucro possível será de R$ 80,00 quando vender 9 pássaros.
35. Para obtêr lucro, deve-se considerar
L(n) > 0. Considerando
L(n) = −200n2 + 1.600n − 2.400 = 0, temos:
(delta)" = (1.600)2 − 4 ⋅ (−200) ⋅ (−2.400) =
= 640.000
Logo:
n = =
Portanto, n’ = 2 e n” = 6.
Como a = −200, logo a < 0, então a concavidade da parábola é voltada para baixo. Portanto, com essas informações, pode-se fazer o seguinte esboço:

Calculando as coordenadas do vértice:
xv = = 4
yV = = 800
Julgando cada uma das afirmações, obtêm-se:
I. Verdadeira. Para 2 < n < 6, a função é positiva, ou seja, o fabricante terá lucro.
II. Verdadeira. O lucro mássimo será de R$ 800,00; portanto, inferior a R$ 1.000,00.
III. Falsa. O lucro será mássimo quando forem vendidas 4 caixas quê equivalem a 4 ⋅ 300 = 1.200, portanto 1.200 picolés.
Resposta: alternativa a.
36. Verificar os valores de x para os quais f assume valores positivos equivale a calcular f(x) > 0. Portanto:
−2x2 + x + 1 > 0
Considerando −2x2 + x + 1 = 0, temos:
(delta)" = (1)2 − 4 ⋅ (−2) ⋅ (1) = 9
Logo: x = =
Assim, x’ = e x” = 1.
Como a = −2, logo a < 0, então a concavidade da parábola é voltada para baixo. Portanto, pode-se fazer o seguinte esboço:

Portanto, para f(x) > 0 o conjunto solução é S= .
Resposta: alternativa e.
Atividades complementares
1. Fazendo um esquema com as informações do enunciado, obtém-se:
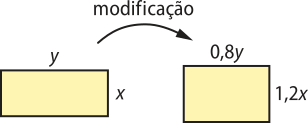
Página trezentos e oitenta e quatro
Do perímetro, vêm: 2x + 2y = 200 ⇒
⇒ x + y = 100
Isolando y, temos: y = 100 − x I
Como a área de um retângulo é calculado por A = b ⋅ h, após a transformação, a área será calculada por:
A = (x ⋅ 1,2) (y ⋅ 0,8) =
= 1,2x ⋅ 0,8y = 96xy II
Substituindo I em II:
A(x) = 0,96 ⋅ x ⋅ (100 − x)
A(x) = 96x − 0,96x2
Resposta: alternativa e.
2. Como às 6 horas começam as atividades da empresa então, nesse momento, deve-se considerar quê x = 0. Portanto, às 7 horas, tem-se x = 1, às 8 horas, tem-se x = 2, às 9 horas, x = 3, e assim por diante. Para encontrar o número de peças produzidas entre 7 h e 9 h, deve-se calcular a diferença ente N(3) e N(1). Considerando quê N(x) = x2 + 10x, tem-se:
N(3) = 32 + 10 ⋅ 3 = 39
N(1) = 12 + 10 ⋅ 1 = 11
Portanto, N(3) − N(1) = 39 − 11 = 28
Resposta: alternativa b.
3. Conforme o enunciado, para 1.910 deve-se considerar quê x = 1. Substituindo esse valor na função, tem-se:
y = ⋅ 12 − ⋅ 1 + ⇒
⇒ y = ⇒
⇒ y = ⇒
⇒ y = =
Portanto, y = 2,47 μg/L.
Para 1.930 deve-se considerar quê x = 3.
Logo:
y = − ⋅ 32 − ⋅ 3 + ⇒
⇒ y = ⇒
⇒ y = =
Portanto, y = 2,19 μg/L.
Logo, o nível decresceu em 0,28 mg/L, pois, 2,47 − 2,19 = 0,28.
Resposta: alternativa e.
4. Considerando as informações contidas no enunciado, tem-se quê:
Como p(2) = 0, então:
0 = m ⋅ 22 + n ⋅ 2 + 1 ⇒ 4m + 2n = − 1.
Como p(−1) = 0, então:
0 = m ⋅ (−1)2 + n ⋅ (−1) + 1 ⇒ m − n = − 1.
Assim, pode-se construir o sistema a seguir:
Multiplicando a segunda equação por 2 e adicionando o resultado à primeira equação, obtém-se m = .
Substituindo esse resultado na primeira equação, obtém-se n = .
Resposta: alternativa a.
5. Com base no enunciado, pode-se obtêr algumas informações importantes:
I) Como o gráfico possui uma única intersecção com a reta y = 2 no ponto (2, 2), pode-se concluir quê o vértice da função tem abscissa e ordenada 2, ou seja, xV = 2 e yV = 2.
II) Como a intersecção da reta x = 0 é o ponto (0, −6), pode-se concluir quê c = −6.
Como o ponto (2, 2) pertence à função, pode-se escrever:
f(2) = a ⋅ 22 + b ⋅ 2 − 6 = 2 ⇒
⇒ 4a + 2b − 6 = 2 ⇒
⇒ 4a + 2b = 8 ⇒ 2a + b = 4
Da afirmação I, pode-se escrever quê:
xv = ⇒ xv = = 2 ⇒ b = −4a
Substituindo essa informação na equação 2a + b = 4, obtêm-se:
2a + b = 4 ⇒ 2a −4a = 4 ⇒ a = −2
b = −4a ⇒ b = −4(−2) ⇒ b = 8
Portanto, a + b + c = −2 + 8 + (−6) = 0.
Resposta: alternativa b.
6. Seja x a quantidade inicial de funcionários e y o valor quê cada um pagaria pelo presente, tem-se:
= y
Com a desistência de dois funcionários, cada um dos restantes contribuiu com R$ 5,00 a mais, ou seja,
= y + 5 ⇒ y = − 5
Daí, tem-se:
= -5 ⇒
⇒ = ⇒
⇒ 200x − 400 = 200x − 5x(x − 2) ⇒
⇒ x2 − 2x − 80 = 0 ⇒ x’ = 8 ou x’’ = 10
Como a quantidade de funcionários é positiva, temos quê x = 10 e cada funcionário restante contribuiu com:
= =25
Resposta: alternativa d.
7. Como a função h é o produto entre as funções f e g, pode-se afirmar quê:
h(x) = f(x) ⋅ g(x) ⇒
⇒ h(x) = (−x + 2) ⋅ (x + 1)
Portanto, as raízes da função h são:
−x + 2 = 0 ⇒ x = 2
ou x + 1 = 0 ⇒ x = −1
Logo, a soma das raízes é 1.
Resposta: alternativa a.
8. Como os pontos (0, −9), (1, 0) e (2, 15) estão contidos em uma função quadrática, pode-se montar as seguintes equações:
−9 = a ⋅ 02 + b ⋅ 0 + c ⇒ c = −9
Substituindo c e os valores das coordenadas dos pontos (1, 0) e (2, 15):
0 = a ⋅ 12 + b ⋅ 1 − 9 ⇒ a + b = 9
15 = a ⋅ 22 + b ⋅ 2 − 9 ⇒ 4a + 2b = 24 ⇒
⇒ 2a + b = 12
Portanto, obtém-se o sistema:
Subtraindo a primeira equação da segunda, obtém-se a = 3. Substituindo o valor de a na primeira equação, obtém-se b = 6. Assim, a lei da função é f(x) = 3x2 + 6x − 9.
Calculando as coordenadas do vértice:
xv = ⇒ xv = = −1
Calculando o discriminante:
(delta)" = (6)2 − 4 ⋅ (3) ⋅ (−9) = 144
yV = = −12
Portanto, o vértice da função quadrática f(x) = 3x2 + 6x − 9 é (−1, −12).
Resposta: alternativa e.
9. Para determinar a altura mássima atingida pela bola após o saque do atleta, calculamos a ordenada do vértice associado a função y:
yv = =
= = = 20,17
Logo, a altura mássima quê a bola chega é de aproximadamente 21,67 m, pois 20,17 + 1,5 = 21,67. êste valor é maior quê a medida da altura dos tetos dos ginásios I, II, III e IV e menor do quê a medida da altura do ginásio V.
Resposta: alternativa d.
10. A receita do lava-jato é representada pelo produto entre a quantidade de clientes e o valor da lavagem. Assim, de acôr-do com a situação do problema, pode-se escrever:
R(x) = (50 − 2x)(20 + x) ⇒
⇒ R(x) = −2x2 + 10x + 1.000
Portanto, a maior arrecadação (yV), bem como o valor da lavagem (xV), é representada pelo vértice da parábola.
Logo, o valor do aumento da lavagem quê maximiza a receita é:
xv = ⇒ xv = = 2, 5
Resposta: alternativa c.
11. A receita do clube é representada pelo produto entre a quantidade de sócios e o valor da mensalidade. Assim, de acôr-do com a situação do problema, pode-se escrever:
R(x) = (800 + 10x)(200 − x) ⇒
⇒ R(x) = −10x2 + 1.200x + 160.000
A maior receita (yV), bem como o valor da mensalidade (xV)para quê isso ocorra, é representada pelo vértice da parábola. Logo, o valor do desconto da mensalidade quê maximiza a receita é:
xv = ⇒ xv = = 60
Portanto, a mensalidade quê o clube deve cobrar para quê tenha a maior receita possível é R$ 140,00 (200 − 60 = 140).
Resposta: alternativa c.
Página trezentos e oitenta e cinco
12. A receita quê uma empresa póde ter é representada pelo produto entre a quantidade de produtos vendidos e o valor de cada um deles. Assim, de acôr-do com a situação do problema, pode-se escrever:
R(x) = p(x) ⋅ x ⇒ R(x) = (400 − x)x ⇒ R(x) = 400x − x2
A maior receita (yV), bem como o valor de cada produto(xV) para quê isso ocorra, é representada pelo vértice da parábola. Logo, a maior receita quê essa empresa póde obtêr é representada por yV.
Calculando o discriminante:
(delta)" = (400)2 − 4 ⋅ (−1) ⋅ (0) = 160.000
Logo:
yV = = 40.000
Resposta: alternativa d.
13. Analisando a inequação N2 − 17N + 16 > 0, pode-se observar quê o gráfico da função y = N2 − 17N + 16 é representado por uma parábola cuja concavidade é voltada para cima, pois a = 1 e, portanto, positivo.
Considerando N2 − 17N + 16 = 0, obtém-se:
(delta)" = (−17)2 − 4 ⋅ (1) ⋅ (16) = 225
Logo:
N = =
Assim, N’ = 1 e N” = 16.
Fazendo o esboço da parábola:

Analisando o esboço, tem-se:
N2 − 17N + 16 = 0 para N = 1 ou N = 16.
N2 − 17N + 16 > 0 para {N ∈ ℝ| N < 1 ou N > 16}.
Sendo assim, a solução do problema consiste em um número menor do quê 1 ou maior do quê 16. Portanto, segundo as alternativas, o número 17 atende à exigência.
Resposta: alternativa d.
14. O enunciado informa quê a função quê relaciona a tempera-túra com o tempo é do 2º grau, portanto da forma f(x) = ax2 + bx + c, em quê f representa a tempera-túra em °C e x representa o tempo em hora. Como o paciente chegou ao posto de saúde com 40 °C de febre, considerando essa informação uma coordenada de um ponto dessa função, entende-se quê o ponto (0, 40) pertence à função. Portanto:
40 = a ⋅ 02 + b ⋅ 0 + c ⇒ c = 40
O enunciado também informa quê duas horas depois a tempera-túra era de 38 °C, ou seja, o ponto (2, 38) também pertence à função. Logo:
40 = a ⋅ 22 + b ⋅ 2 + 40 ⇒ 4a + 2b = −2
Como o ponto mássimo da tempera-túra, o vértice da parábola, ocorre 30 minutos (0,5 hora) após a chegada do paciente, pode-se concluir quê (0,5; yV)pertence à função. Logo:
xv = = 0, 5 ⇒ a = −b
Substituindo esse resultado na equação anterior:
4a + 2b = −2 ⇒ −4b + 2b = −2 ⇒ b = 1
E, consequentemente, a = −1.
Portanto, a função é f(x) = −x2 + x + 40.
Calculando o discriminante:
(delta)" = (1)2 − 4 ⋅ (−1) ⋅ (40) = 161
yV = = 40, 25
Logo, 40,25 − 3 = 37,25.
Resposta: alternativa 02.
15. Para melhor compreensão, vamos transferir os dados da Figura 2 para o plano cartesiano. Assumindo quê o ponto quê determina a altura H da igreja tenha abscissa igual a zero, então, pela simetria da figura, temos a representação:
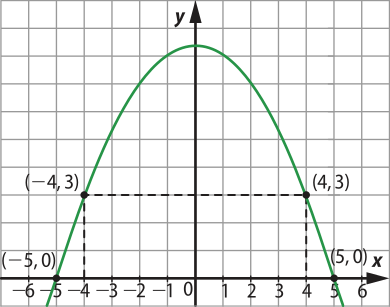
Assim, temos o gráfico de uma parábola f(x) = ax2 + bx + c quê passa pêlos pontos (−4, 3), (4, 3) e cujas raízes são (−5, 0) e (5, 0). Observe quê:
= 5 − 5 ⇒ b = 0
= 5 ⋅ (− 5) ⇒ c = −25a
Logo, f(x) = ax2 − 25a = a(x2 − 25). Para determinar o valor de a, avaliamos o ponto (4, 3) na função f:
3 = f(4) = a((4)2 − 25) = −9a ⇒ a =
Então, f(x) = (x2− 25). Dessa forma, a altura procurada H, em métro, é atingida em x = 0:
H = f(0) = (02 − 25) =
Resposta: alternativa d.
Capítulo 5 • Função exponencial
Atividades
1. a) =
Utilizando uma calculadora, obtém-se a aproximação 3,344.
b)
Utilizando uma calculadora, obtém-se a aproximação 3,162.
c)
Utilizando uma calculadora, obtém-se a aproximação 1,260.
d) 30,25 =
Utilizando uma calculadora, obtém-se a aproximação 1,316.
e)
Utilizando uma calculadora, obtém-se a aproximação 1,331.
f)
Utilizando uma calculadora, obtém-se a aproximação 0,577.
2. a) 34 ⋅ 35 = 34 + 5 = 39
b) (x3)4 = x3 ⋅ 4 = x12
c) 79 ⋅ 74 = 79 + 4 = 713
d) = 1012 − 5 = 107
e) (103)2 = 103 ⋅ 2 = 106
f) an + 1 ⋅ an − 2 = an + 1 + n − 2 = a2n − 1
Página trezentos e oitenta e seis
3. a) = = 3−2
b) = = 10−4
c) = = 2−5
d) = = = 6−2
e) = = 2−1
f) = = a−2
4. a) 51,5 ≃11,180
b) 121_ 4 ≃1,861
c) 280,25 ≃2,300
d) 34,5 ≃140,296
e) 22,6 ≃6,063
f) ≃1,894
g) ≃11, 665
h) ≃53, 957
5. De acôr-do com a definição, um número representado em notação científica é da forma a ⋅ 10n, em quê 1 ≤ a < 10 e n é um número inteiro.
a) 299.793.458 ≃ 2,998 ⋅ 108
b) 12.742 ≃ 1,274 ⋅ 104
c) 0,00011 = 1,1 ⋅ 10−4
6. Como em cada item a seguir há um produto ou uma razão entre notações científicas, podem-se reorganizar os fatores de cada notação de acôr-do com a operação indicada no respectivo item.
a) (2,0 ⋅ 103) ⋅ (4,0 ⋅ 10−5) =
= 2,0 ⋅ 4,0 ⋅ 103 ⋅ 10−5 =
= (2,0 ⋅ 4,0) ⋅ 103 − 5 = 8 ⋅ 10−2
b) (5,2 ⋅ 106) ∶ (1,3 ⋅ 10−3) =
= (5,2 ∶ 1,3) ⋅ (106 − (−3)) = 4 ⋅ 109
c) (1,5 ⋅ 103) ⋅ (2,0 ⋅ 10−5) ⋅ (4,0 ⋅ 10−8) =
= (1,5 ⋅ 2,0 ⋅ 4,0) ⋅ (103 − 5 − 8)) =
= 12 ⋅ 10−10 = 1,2 ⋅ 10−9
7. a) Desenvolvendo as potências em cada item:
a = 33 = 27
b = (−2)3 = −8
c = 3−2 = =
d = (−2)−3 = =
b) A sequência dos números a, b, c e d escritos na ordem crescente é: −8;; ; 27
8. Para calcular a mêtáde de 22012, deve-se dividir o número por dois, logo:
= 22012 − 1 = 22011
9. Aplicando as propriedades da potenciação:
4x + 2 − (x − 2) ∶ 4x − (x − 1) = =
= = 43 = 64
10. Observando a expressão , pode-se colocar310 em evidência no numerador e denominador.
Logo:
![]() = = = 1
= = = 1
11. Vamos analisar os algarismos das unidades nas potências de 12. Observa-se quê, nas multiplicações de 12 por 12, o algarismo das unidades é obtído pelo produto 2 ⋅ 2, dêêsse modo:
121 termina em 2
122 termina em 4, pois 2 ⋅ 2 = 4
123 termina em 8, pois 2 ⋅ 2 ⋅ 2 = 8
124 termina em 6, pois 2 ⋅ 2 ⋅ 2 ⋅ 2 = 16
125 termina em 2, pois 2 ⋅ 2 ⋅ 2 ⋅ 2 ⋅ 2 = 32
126 termina em 4, pois 2 ⋅ 2 ⋅ 2 ⋅ 2 ⋅ 2 ⋅ 2 = 64
127 termina em 8, pois 2 ⋅ 2 ⋅ 2 ⋅ 2 ⋅ 2 ⋅ 2 ⋅ 2 = 128
128 termina em 6, pois 2 ⋅ 2 ⋅ 2 ⋅ 2 ⋅ 2 ⋅ 2 ⋅ 2 ⋅ 2 = 256
Observe quê uma potência de 12 terminará em 6 a cada potência cujo expoente é múltiplo de 4. Assim, dentro do intervalo 78 ≤ n ≤ 155, deve-se encontrar o maior múltiplo de 4.
Como o résto da divisão de 155 por 4 é 3, então o maior múltiplo de 4 será 152.
Portanto, n = 152.
12. Para simplificar cada expressão devem-se aplicar as propriedades da potenciação.
a)
b) = 243
c) =
= 2−2 =
d) = = 7(4,3 − 2,6) − (−0,3) = 72 = 49
e) =
= =
= 5 ⋅ (4−1 ⋅ 5)= 52 ⋅ 2−2 = =
13. Nas passagens 1 e 2, as propriedades de potenciação foram aplicadas corretamente. Porém, na passagem 3, há um êrro com relação ao sinal, pois o sinal negativo (operação) não foi distribuído entre os termos do subtraendo. Corrigindo:![]() Portanto, a resposta correta é 25.
Portanto, a resposta correta é 25.
14. Chamando o resultado da expressão de A e usando as propriedades das potências:
A = ⇒
⇒ A = ⇒
⇒ A = 3 ⋅ 10 ⇒ A = 30
15. Aplicando as propriedades da potenciação:
= =
= =
16. Aplicando as propriedades de potenciação.
xyz = (22)3 ⋅ 223 ⋅ 232 = 26 ⋅ 28 ⋅ 29 = 223
17. Fatorando os termos da expressão e aplicando as propriedades das potências:
=
= =
= ![]() = =
= =
= 1010 −20 = 10−10
18. Fatorando os termos da expressão e aplicando as propriedades da potenciação:
=
= ![]() =
=
= = =
19.
a) f(x) = 5x ⇒ função crescente, pois a > 1.
b) f(x) = ⇒ função decrescente, pois 0 < a < 1.
c) f(x) = 2−x = (2−1)x = ⇒ função decrescente, pois 0 < a < 1.
d) f(x) = = ⇒ função crescente, pois a > 1.
20. a) f(x) = 3x
Considerando alguns pontos para x e substituindo na lei da função:
x |
f(x) = 3x |
|---|---|
−1 |
|
0 |
1 |
1 |
3 |
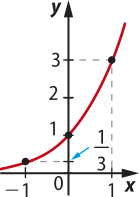
Portanto, o domínio é D(f) = ℝ e a Im(f) = ℝ*+.
Página trezentos e oitenta e sete
b) f(x) = 2x + 1
Considerando alguns pontos para x e substituindo na lei da função:
x |
f(x) = 2x + 1 |
|---|---|
−2 |
|
−1 |
1 |
0 |
2 |
1 |
4 |
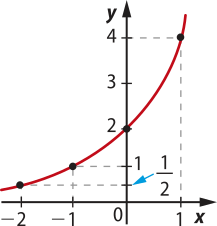
Portanto, o domínio é D(f) = ℝ e a Im(f) = ℝ*+.
c) f(x) =
Considerando alguns pontos para x e substituindo na lei da função:
x |
f(x) = |
|---|---|
−1 |
3 |
0 |
1 |
1 |
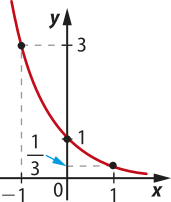
Portanto, o domínio é D(f) = ℝ e a Im(f) = ℝ*+.
d) f(x) = 2x + 1
Considerando alguns pontos para x e substituindo na lei da função:
x |
f(x) = 2x + 1 |
|---|---|
−1 |
|
0 |
2 |
1 |
3 |
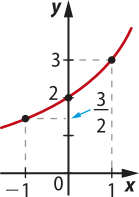
Portanto, o domínio é D(f) = ℝ e a Im(f) = {y ∈ ℝ | y > 1}.
21. a) Considerando alguns valores para x e substituindo em ambas as funções, obtêm-se o qüadro e os gráficos a seguir.
t |
2t |
2t |
|---|---|---|
0 |
0 |
1 |
1 |
2 |
2 |
2 |
4 |
4 |
3 |
6 |
8 |
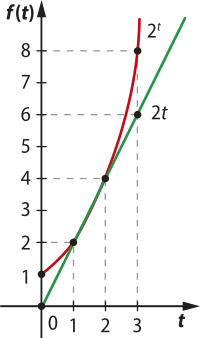
b) Sim, ao observar os gráficos é possível perceber quê eles se interceptam em t = 1 e t = 2, com t em hora.
c) Ambas são funções crescentes.
d) Para t = 3, tem-se:
f(t) = 2t ⇒ f(3) = 2 ⋅ (3) = 6
f(t) = 2t ⇒ f(3) = 23 = 8
Logo, 8 − 6 = 2, ou seja, 2.000 bactérias.
22.
a) A amostra de bactérias aumentou no intervalo entre 20 °C e 60 °C; diminuiu no intervalo entre 80 °C e 120 °C e manteve-se estável nos intervalos entre 0 °C e 20 °C e entre 60 °C e 80 °C.
b) Para calcular a quantidade de bactérias, deve-se relacionar a tempera-túra com o intervalo e a função. Portanto:
• 30 °C ⇒ f(30) = 20,1(30 −10) = 22 = 4
Ou seja, 400.000 bactérias.
• 50 °C ⇒ f(50) = 20,1(50 −10) = 24 = 16
Ou seja, 1.600.000 bactérias.
• 90 °C ⇒ g(90) = 32 ⋅ 2−0,2(90 −80) = 23 = 8
Ou seja, 800.000 bactérias.
• 110 °C ⇒ g(110) = 32 ⋅ 2−0,2(110 −80) = 2−1 = 0,5
Ou seja, 50.000 bactérias.
23. Para a função do tipo f(x) = ax sêr decrescente, necessariamente deve-se ter quê 0 < a < 1. Assim:
0 < k − 3 ⇒ 3 < k
k − 3 < 1 ⇒ k < 4
Logo: 3 < k < 4
24. Calculado o valor numérico para cada valor de x nas respectivas funções:
x = −2 |
x = −1 |
x = 0 |
x = 1 |
x = 2 |
x = 3 |
|
|---|---|---|---|---|---|---|
lei da função: f(x) = 3x |
1 |
3 |
9 |
27 |
||
lei da função: g(x) = 3x + 2 |
3 |
5 |
11 |
29 |
||
lei da função: h(x) = 3x − 2 |
1 |
3 |
a) Considerando os pontos do qüadro, é possível plotar os gráficos f, g e h:
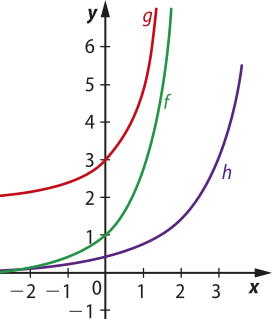
b) Analisando os gráficos, é possível observar quê as funções são crescentes.
c) Os domínios e as imagens de cada função são:
D(f) = ℝ e Im(f) = ℝ*+;
D(g) = ℝ e Im(g) = {y ∈ ℝ | y > 2};
D(h) = ℝ e Im(h) = ℝ*+
Página trezentos e oitenta e oito
d) O gráfico de m equivale ao gráfico de f com um deslocamento de todos os pontos dêêsse gráfico em duas unidades na vertical para baixo.
e) O gráfico de q equivale ao gráfico de f com um deslocamento de todos os pontos dêêsse gráfico em duas unidades na horizontal para a esquerda.
f)
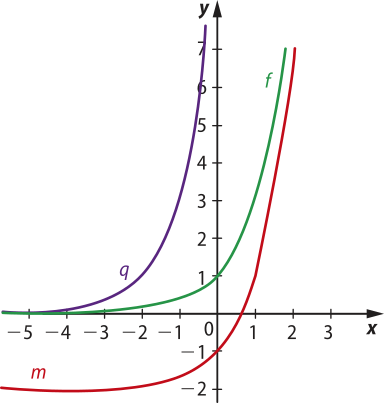
25. a) Considerando a taxa de variação média como a média do rendimento entre o primeiro e sexto mês, pode-se calcular como:
TMÉDIA = = 3,524
Portanto, o rendimento médio no período foi de R$ 3,52.
b) Como o rendimento é de 0,35% ao mês e o valor de investimento inicial é de R$ 1.000,00, pode-se entender quê a lei de formação da função quê calcula o valor disponível é:
f(x) = 1.000 ⋅ (1 + 0,0035)x ⇒ f(x) = 1.000 ⋅ (1,0035)x
c) Considerando um período de 12 meses e utilizando uma calculadora, o cliente obterá um saldo disponível de:
f(12) = 1.000 ⋅ (1,0035)12 ⇒ f(12) ≃ R$ 1.042,82
26. Para resolver as equações exponenciais, pode-se manter ambos os membros na mesma base e igualar os expoentes.
a) 2x = 26 ⇒ x = 6
S = {6}
b) 10x = 103 ⇒ x = 3
S = {3}
c) 32x = 35 ⇒ 2x = 5 ⇒ x =
S =
d) = ⇒ x = 5
S = {5}
e) = ⇒ = ⇒ 4x = 1 ⇒ x =
S =
f) 4x = 4−3 ⇒ x = −3
S = {−3}
g) 3x = ⇒ x =
S =
h) 4x = 3 ⇒ 22x = ⇒ 2x = ⇒ x =
S =
27. Considerando a função f(x) = 52x − 1, para calcular o valor de x, devem-se aplicar os conceitos de função, ou seja:
a) 52x − 1 = 125 ⇒ 52x − 1 = 53 ⇒ 2x −1 = 3 ⇒ x = 2
b) 52x − 1 = 1 ⇒ 52x − 1 = 50 ⇒ 2x −1 = 0 ⇒ x =
c) 52x − 1 = 0 ⇒ ∄ x ∈ ℝ | 52x − 1 = 0
d) 52x − 1 = ⇒ 52x − 1 = 5−1 ⇒ 2x − 1 = −1 ⇒ x = 0
28. Para resolver as equações, devem-se manter ambos os membros da equação exponencial na mesma base e, em seguida, igualar os expoentes. Logo:
a) 2x − 2 = ⇒ 2x − 2 = 23 − (x − 3) ⇒ 2x − 2 = 26 − x ⇒
⇒ x − 2 = 6 − x ⇒ x = 4
S = {4}
b) 252x + 2 = ⇒ 52(2x + 2) = 5−5x + 1 ⇒ 4x + 4 = −5x + 1 ⇒
⇒ 9x = −3 ⇒ x=
S =
c) 5x 2 − 2∶ 25 = ⇒ 5x 2 − 4 = 53x ⇒ x2 − 4 = 3x ⇒
⇒ x2 − 3x − 4 = 0 ⇒ x(minutos)" = −1 e x(segundos)" = 4
S = {−1, 4}
d) = ⇒ = 3−3 ⇒ = −3 ⇒ x =
S=
29. Aplicando as técnicas de fatoração no numerador e denominador no primeiro membro da equação:
= 2 ⇒ ![]() = 2 ⇒ = 2
= 2 ⇒ = 2
Fazendo 2x = y:
= 2 ⇒ = 2 ⇒ y = 2
Portanto, 2x = 21, ou seja, x = 1.
30. Considerando t = 0 o instante em quê havia 200 bactérias, tem-se N0 = 200. Após 12 horas, havia 600 bactérias. Então:
600 = 200 ⋅ K12 ⇒ K12 = 3
Após 48 horas do início da observação, tem-se:
N(48) = 200 ⋅ K48 = 200 ⋅ (K12)4 = 200 ⋅ (3)4 = 200 ⋅ 81 = 16.200
Após 48 horas existirão 16.200 bactérias.
31. Para resolver a equação coloca-se 2x em evidência. Logo:
2x + 1 + 2x + 2 + 2x + 3 = 224
2x ⋅ 2 + 2x ⋅ 4 + 2x ⋅ 8 = 25 ⋅ 7
2x (2 + 4 + 8) = 25 ⋅ 7
= 25
2x + 1 = 25 ⇒ x = 4
S = {4}
32. Para resolver a equação, mantém-se ambos os membros com um termo e na mesma base. Para isso, ultiliza-se as propriedades da potenciação.
33x − 1 ⋅ 32(2x + 3) =33(3 − x)
33x − 1 + 4x + 6 = 39 − 3x ⇒ 7x + 3x = 9 + 1 − 6 ⇒ 10x = 4 ⇒ x =
33. Para resolver a equação, coloca-se 8x em evidência no primeiro membro da equação exponencial:
8x = 292 ⇒ 8x =292 ⇒ 8x =32
Página trezentos e oitenta e nove
Simplificando a equação e deixando ambos os membros da equação na base 2:
23x = 25 ⇒ x=
S=
34. Aplicando as propriedades da potenciação, é possível escrever a equação da seguinte maneira:
1x + 5x + 25x = 3 ⇒ 52x + 5x − 2 = 0
Substituindo 5x = y, obtêm-se:
y2 + y − 2 = 0
Resolvendo a equação do 2º grau, obtêm-se as raízes y(minutos)" = 1 e y(segundos)" = −2.
Logo:
5x = 1 ⇒ 5x = 50 ⇒ x = 0
5x = −2 ⇒ Não há um número real quê satisfaça a equação.
Portanto, S = {0}.
35. Aplicando as propriedades da potenciação, é possível escrever a equação da seguinte maneira:
⇒
⇒ 310x − 2 − 8x +12 = 315 − 9x − 2x + 5 ⇒
⇒ 32x +10 = 3−11x +20 ⇒
⇒ 2x + 10 = −11x + 20 ⇒ x =
Portanto, S = .
36. Substituindo os dados fornecidos pelo enunciado na fórmula:
m = m0 ⇒1, 25 = 5 ⋅ ⇒
⇒ =5 ⇒ = = 5 ⋅ ⇒
⇒ 2−2 = ⇒
⇒ = 2 ⇒ t = 10.800
Portanto, em 10.800 anos.
37. Aplicando as propriedades da potenciação, é possível escrever a equação da seguinte maneira:
3 ⋅ 5x2 + 3x2 ⋅ 3 − 8 ⋅ 3x2 = 0 ⇒
⇒ 3 ⋅ 5x2 + 3x2 ⋅ (3 − 8) = 0 ⇒
⇒ 3 ⋅ 5x2 = 3x2 ⋅ 5 ⇒ =
⇒ x2 = 1 ⇒ x(minutos)" = −1 ou x(segundos)" = 1
S = {−1, 1}
38. Aplicando as propriedades da potenciação, é possível escrever a equação da seguinte maneira:
− = −1 ⇒
⇒ 32x − 1 − ⋅ 3x + 1 = 0 ⇒
⇒ − ⋅ 3x + 1 = 0
Substituindo 3x = y:
− y + 1 = 0 ⇒ y2 − 4y + 3 = 0
Resolvendo a equação do 2º grau, obtêm-se as raízes y(minutos)" = 1 e y(segundos)" = 3.
Como 3x = y:
3x = 3 ⇒ x = 1
3x = 1 ⇒ 3x = 30 ⇒ x = 0
S = {0, 1}
39. Aplicando as propriedades da potenciação, é possível escrever a equação da seguinte maneira:
s(x) = 3x − 1 + 3x ⇒ s(x) = + 3x ⇒
⇒ s(x) = 3x ⇒ s(x) = 3x
s(x) = 4 ⇒ 3x ⋅ = 4⇒ 3x = 3 ⇒ x = 1
40. Considerando a função f(x) = 3x, podem-se encontrar os termos f(x + 1) e f(−x + 4).
f(x + 1) = 3x + 1
f(−x + 4) = 3−x + 4
Como f(x + 1) + f(−x + 4) = 36, então:
3x + 1 + 3−x + 4 = 36 ⇒
⇒ 3x ⋅ 3 + 3−x ⋅ 34 = 36
Substituindo 3x = y:
3y + =36 ⇒ y2 − 12y + 27 = 0
Resolvendo a equação do 2º grau, obtêm-se as raízes y(minutos)" = 3 e y(segundos)" = 9
Como 3x = y:
3x = 9 ⇒ 3x = 32 ⇒ x = 2
3x = 31 ⇒ x = 1
Portanto, x = 2 ou x = 1.
41. Resposta pessoal. Exemplo de questão: O reservatório terá a mêtáde da sua capacidade após quantos meses de estiagem?
V(t) = V0 ⋅ 2−0,05t ⇒
⇒ = V0 ⋅ 2−0,05t ⇒ 2−1 = 2−0,05t
Igualando os expoentes:
−1 = −0,05t ⇒ t = 20
Portanto, a represa terá a mêtáde da sua capacidade após 20 meses.
42. Para resolver as inequações, devem-se deixar ambos os membros na mesma base e verificar se a base é maior do quê 1 ou pertence ao intervalo]0, 1[.
a) 2x2 − 3x ≥ 2−2
Como a base é maior do quê 1, deve-se manter o sinal da inequação entre os expoentes. Logo:
x2 − 3x + 2 ≥ 0
Resolvendo a equação x2 − 3x + 2 = 0, obtêm-se as raízes x(minutos)" = 2 e x(segundos)" = 1.

Como os intervalos em quê a função quadrática é não negativa são x ≤ 1 ou x ≥ 2, o conjunto solução será
S = {x ∈ ℝ | x ≤ 1 ou x ≥ 2}.
b)
Como a base é positiva e menor do quê 1, deve-se inverter o sinal da inequação entre os expoentes. Logo:
2x> 3 ⇒ x >
Portanto, S = .
c) (0,2)x − 2 > (0,2)0
Como a base é positiva e menor do quê 1, deve-se inverter o sinal da inequação entre os expoentes. Logo:
x − 2 < 0 ⇒ x < 2
Portanto, S = {x ∈ ℝ | x < 2}.
d) 2x + 1 ⋅ 22(x − 1) ≤ 2−5 ⇒ 2x + 1 + 2x − 2 ≤ 2−5
Como a base é maior do quê 1, deve-se manter o sinal da inequação entre os expoentes. Logo:
3x − 1 ≤ −5 ⇒ x ≤
Portanto, S = .
e) ⇒
⇒
Como a base é maior do quê 1, deve-se manter o sinal da inequação entre os expoentes. Logo:
5x + 3 > 12x + 9 ⇒ −7x > 6 ⇒
⇒ x <
Portanto, S = .
f) ≥ 0,008 ⇒
⇒ ≥ (0,2)3
Como a base é positiva e menor do quê 1, deve-se inverter o sinal da inequação entre os expoentes. Logo:
x2 − 2x ≤ 3 ⇒ x2 − 2x − 3 ≤ 0
Resolvendo a equação x2 − 2x − 3 = 0, obtêm-se as raízes x(minutos)" = −1 e x(segundos)" = 3.

Portanto, o conjunto solução será
S = {x ∈ ℝ | −1 ≤ x ≤ 3}.
43. Para resolver a inequação pode-se começar colocando o fator 3x em evidência.
Assim:
3x + 1 + 32 + x > 108
3x (3 + 9) > 108
3x > 9 ⇒ 3x > 32
Como a base é maior do quê 1, deve-se manter o sinal da inequação entre os expoentes. Portanto, x > 2.
S = {x ∈ ℝ | x > 2}
44. Para a expressão representar um número real, o radicando deve sêr maior ou igual a 0. Logo:
2x + 2x + 1 − 12 ≥ 0
Para resolver a inequação, deve-se colocar o fator 2x em evidência. Assim:
2x (1 + 2) ≥ 12 ⇒ 2x ≥ 4 ⇒ 2x ≥ 22
Como a base é maior do quê 1, deve-se manter o sinal da inequação entre os expoentes. Portanto x ≥ 2.
S = {x ∈ ℝ | x ≥ 2}
Página trezentos e noventa
45. Para definir o domínio de ambas as funções, deve-se ter o radicando maior ou igual a 0.
a) 2x − 21 − x ≥ 0 ⇒ 2x ≥ 21 − x
Como a base é maior do quê 1, deve-se manter o sinal da inequação entre os expoentes, logo:
x ≥ 1 − x ⇒ x ≥
D(f) =
b) (0,1)x2 − 5x − (0,1)−6 ≥ 0 ⇒
⇒ (0,1)x2 − 5x ≥ (0,1)−6
Como a base é positiva e menor do quê 1, deve-se inverter o sinal da inequação entre os expoentes. Logo:
x2 − 5x + 6 ≤ 0
Ao resolver a equação x2 − 5x + 6 = 0, obtêm-se as raízes x’ = 2 e x” = 3.
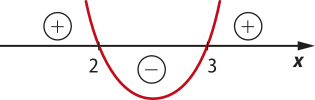
D(g) = {x ∈ ℝ | 2 ≤ x ≤ 3}
46. Considerando a inequação
4x − 10 ⋅ 2x + 16 < 0, pode-se reescrevê-la da seguinte maneira:
(2x)2 − 10 ⋅ 2x + 16 < 0
Substituindo 2x = y, temos:
y2 − 10y + 16 < 0.
Resolvendo a equação y2 − 10y + 16 = 0, obtêm-se as raízes y(minutos)" = 2 e y(segundos)" = 8.

Portanto, 2 < y < 8.
Como 2x = y, então:
2 < 2x < 8 ⇒ 21 < 2x < 23 ⇒ 1 < x < 3
Portanto, S = {x ∈ ℝ | 1 < x < 3}.
47. Para resolver a inequação
21 + x + ≥ , ambos os membros da inequação devem ter um termo com a mesma base. Logo:
21 + x + _ ≥ _ ⇒ 21 + x ≥ _ − ⇒
⇒ 21 + x ≥ ⇒ 21 + x ≥ ⋅ 2 ⇒
⇒ 21 + x ≥
Como a base é maior do quê 1, deve-se manter o sinal da inequação entre os expoentes. Assim:
1 + x ≥ ⇒ x ≥
Portanto, S = .
48. Para resolver a inequação, deve-se deixar cada membro na mesma base, ou seja:
1 < ≤ 64 ⇒ 40 < ≤ 43 ⇒
⇒ 0 < ≤ 3 ⇒ 0 < x ≤ 12
Como a solução é representada por números inteiros, então o conjunto solução é S = {1, 2, 3, 4, 5, 6, 7, 8, 9, 10, 11, 12}.
49. Para encontrar a solução da inequação, devem-se deixar ambos os membros com um termo de mesma base. Logo:
5x2 ⋅ 52x − 1 ⋅ 5−3 ≤ 5−1 ⇒ 5x2 + 2x − 1 − 3 ≤ 5−1
Como a base é maior do quê 1, deve-se manter o sinal da inequação entre os expoentes. Assim:
x2 + 2x − 3 ≤ 0
Resolvendo a equação x2 + 2x − 3 = 0, obtêm-se as raízes x(minutos)" = −3 e x(segundos)" = 1.

Portanto, S = {x ∈ ℝ | −3 ≤ x ≤ 1}.
50. Resposta pessoal. Exemplo de quêstão: Qual é o tempo mínimo necessário para quê a planta estudada atinja uma altura maior do que 90 cm?
O problema propõe quê se calculem os possíveis valores de t para quê h(t) > 90.
Logo:
2,52 + 0,04 ⋅ 30,14t > 90 ⇒
⇒ 30,14t > ⇒ 30,14t > 37
Como a base é maior do quê 1, deve-se manter o sinal da inequação entre os expoentes. Assim:
0,14t > 7 ⇒ t > 50
O tempo mínimo será de 50 dias.
51. Para resolver a inequação, aplicam-se as propriedades da potenciação para deixar as bases, em ambos os membros, iguais. Logo:
Como a base é um número quê pertence ao intervalo]0, 1[, então deve-se inverter o sinal da inequação entre os expoentes, assim: x2 − 4x + 3 < 0.
Resolvendo a equação x2 − 4x + 3 = 0, obtêm-se as raízes x(minutos)" = 1 e x(segundos)" = 3.

Portanto, 1 < x < 3.
Desse modo, x pertence ao intervalo ]1, 3[.
Resposta: alternativa d.
52. Para encontrar a solução, deve-se manter a mesma base em ambos os lados da inequação. Logo:
> 4 ⇒ > 22 ⇒
⇒ > 22 ⇒
⇒ −x2 + 8x − 7 > 0
Resolvendo essa inequação do 2º grau, obtém-se: x(minutos)" = 1 ou x(segundos)" = 7.

Logo, apenas dois números inteiros ímpares pertencem ao intervalo]1, 7[, a saber: 3 e 5.
Resposta: alternativa b.
53. Considerando t = 2, encontram-se os seguintes valores numéricos de cada função:
F1 (2) = 22 + 96 = 4 + 96 = 100
F2 (2) = 9 ⋅ 22 + 64 = 9 ⋅ 4 + 64 =
= 36 + 64 = 100
Ou seja, para t = 2 pode-se concluir quê
B1 = B2.
Considerando t = 3:
F1 (3) = 32 + 96 = 9 + 96 = 105
F2 (3) = 9 ⋅ 32 + 64 = 9 ⋅ 9 + 64 =
= 81 + 64 = 145
Assim, pode-se concluir quê, após o instante t = 2, o crescimento de B1 será menor do quê o de B2.
Resposta: alternativa b.
Atividades complementares
1. Considerando os dados fornecidos pelo enunciado:
x2 + 1 = + 1 =
= + 1 = + 1 =
Resposta: alternativa b.
2. Aplicando as propriedades da fatoração:
Resposta: alternativa e.
3. Resolvendo ambas as equações:
⇒
⇒ ⇒ x = −4
= 729 ⇒ = 36 ⇒
⇒ y2 = 38 ⇒ y = 81
Portanto: y + 3x = 81 + 3(−4) = 69
Resposta: alternativa 04.
4. Resolvendo a expressão:
(2−3,5 ⋅ )+ 0,125 + =
= = 1
Resposta: alternativa a.
5. De acôr-do com o enunciado, a classificação espectral do Sol é G2, cuja tempera-túra é de 5.770 K. Conforme a tabéla, quê usa o Sol como unidade, estrelas dessa classificação possuem luminosidade, massa e raio iguais aos do Sol. A tempera-túra da estrela é 5 vezes a tempera-túra do Sol. Utilizando os dados de tempera-túra de uma estrela da mesma classificação espectral do Sol, temos: 5.770 ⋅ 5 = 28.850 K
Isso corresponde a uma estrela de classificação espectral B0. Pela tabéla, estrelas dessa classificação possuem uma luminosidade de 2 ⋅ 104, ou seja, 20.000. Como os dados da tabéla utilizam a luminosidade do Sol como unidade, a ordem de grandeza da luminosidade dessa estrela é 20.000 vezes a luminosidade do Sol. Resposta: alternativa a.
Página trezentos e noventa e um
6. Segundo os dados fornecidos pelo gráfico, pode-se concluir quê os pontos (2, 8) e (0, −1) pertencem ao gráfico da função f. Logo:
f(0) = a ⋅ 30 + b ⇒ a + b = −1
f(2) = a ⋅ 32 + b ⇒ 9a + b = 8
Portanto, chega-se no sistema:
Subtraindo a primeira equação da segunda, tem-se: a = . Substituindo o valor de a na primeira equação:
a + b = −1 ⇒ b= −1 − ⇒ b =
Portanto, pode-se afirmar:
a ⋅ b = ⋅
Logo, é um número situado entre −4 e −1.
Resposta: alternativa a.
7. Segundo o enunciado, deve-se calcular a população de bactérias depois de 20 minutos.
Porém, a função é dada em hora, por isso deve-se transformar 20 minutos em horas, ou seja: .
Portanto:
p(t) = 40 ⋅ 23t ⇒ p = 40 ⋅ ⇒
⇒ p = 80
Portanto, após 20 minutos, a quantidade inicial de bactérias foi duplicada.
Resposta: alternativa d.
8. Segundo as informações contidas no gráfico, pode-se observar quê os pontos (0, 60.000) e (1, 54.000) pertencem à função f. Logo:
f(0) = b ⋅ a0 ⇒ 60.000 = b
f(1) = 60.000 ⋅ a1 ⇒
⇒ 54.000 = 60.000 ⋅ a ⇒ a = 0,9
Portanto, a função de depreciação é
f(t) = 60.000 ⋅ 0,9t.
Então, ao calcular f(2):
f (2) = 60.000 ⋅ 0,92 ⇒ f(2) = 48.600
Resposta: alternativa c.
9. Considerando quê, em uma condição inicial t = 0, a quantidade de substância é 800 g; pode-se afirmar quê:
Q(t) = k ⋅ 2−0,5t ⇒ Q(0) = k ⋅ 2−0,5 ⋅ 0 ⇒
⇒ k = 800
Como 25% de 800 é 200, o tempo necessário para quê a quantidade de uma substância chegue a esse valor é:
200 = 800 ⋅ 2−0,5t ⇒ 2−2 = 2−0,5t ⇒ t = 4
Resposta: alternativa b.
10. Aplicando as propriedades da potenciação:
= ⇒ = 3−3 ⇒
⇒ 3−3x + 3 = 3−3 ⇒
⇒ −3x + 3 = −3 ⇒ x = 2
Resposta: alternativa d.
11. Aplicando as propriedades da potenciação na equação 32k − 4 ⋅ 3k + 3 = 0, pode-se escrevê-la da seguinte forma:
32k − 4 ⋅ 3k + 3 = 0 ⇒ (3k)2 − 4 ⋅ 3k + 3 = 0
Fazendo 3k = y, tem-se y2 − 4y + 3 = 0 e, resolvendo essa equação do 2º grau, obtêm-se as raízes y(minutos)" = 3 e y(segundos)" = 1.
y = 3 ⇒ 3k = 3 ⇒ k = 1 ⇒ k2 = 1
y = 1 ⇒ 3k = 30 ⇒ k = 0 ⇒ k2 = 0
Resposta: alternativa b.
12. Considerando a equação presente no enunciado e aplicando as propriedades de potência, temos:
− 8 ⋅ − 9 = 0 ⇒
⇒ − 8 ⋅ − 9 = 0 ⇒
⇒ − 8 ⋅ − 9 = 0
Substituindo = y:
y2 − 8 ⋅ y − 9 = 0
Resolvendo a equação do 2º grau, obtêm-se as raízes y’ = −1 e y” = 9. Note quê a raiz y’ = −1 não é solução dentro do conjunto dos números reais; logo, para y” = 9, temos:
= 9 ⇔ = 32 ⇔ = 2 ⇔ x = 4
Assim, a solução fica entre 3,5 < k < 5,5.
Resposta: alternativa d.
13. De acôr-do com o enunciado, depois de 10 dias, ou seja, t = 10, a população de insetos reduziu à quarta parte da população inicial, ou seja, . Logo:
N(t) = N0⋅ 2kt ⇒ = N0⋅ 2k ⋅10 ⇒
⇒ 2−2 = 210k ⇒ k = −5−1
Resposta: alternativa b.
14. Como V(t) = 10.000 ⋅ (0,9)t é a função quê calcula a depreciação, então:
V(t) = 10.000 ⋅ (0,9)t ⇒
⇒ 8.100 = 10.000 ⋅ (0,9)t ⇒
⇒ (0,9)2 = (0,9)t ⇒ t = 2
Resposta: alternativa a.
15. I. Verdadeira.
Considerando quê o instante inicial é x = 0:
q(0) = 25 − 0,5 ⋅ 0 = 32
Ou seja, no instante em quê o processo foi iniciado, a quantidade de poluente era 32 mg/L.
II. Verdadeira.
Considerando o instante x = 4:
q(4) = 25 − 0,5 ⋅ 4 = 8
Ou seja, um quarto da quantidade inicial.
III. Falsa.
Considerando os instantes já calculados q(0) = 32 e q(4) = 8, pode-se perceber quê a função não é crescente.
IV. Verdadeira.
Considerando x = 2:
q(2) = 25 − 0,5 ⋅ 2 = 16
Ou seja, a mêtáde da quantidade existente no início do processo.
V. Verdadeira.
Considerando q(t) = 4:
25 − 0,5t = 22 ⇒ 5 − 0,5t = 2 ⇒ 3 = 0,5t ⇒
⇒ t = 6
Portanto, somente na 6ª hora, após iniciado o processo, é quê a quantidade de partículas atinge o nível recomendado.
16. Para calcular o tempo quê a lagoa vai conter 9.271 peixes, deve-se considerar quê n(T) = 9.271. Logo:
n(T) = 10.000 − ⇒
⇒ 9.271 = 10.000 − ⇒
⇒ = 10.000 − 9.271 ⇒
⇒ = 729 ⇒ = 36
Portanto, − 2 = 6 ⇒ = 8 ⇒ T = 24.
Resposta: alternativa c.
17. Considerando quê a função de resfriamento é T(t) = TA + (alfa)" ⋅ 3(beta)"t e quê, segundo o enunciado, os pontos (90, 0) e (270, −16) pertencem a ela, então pode-se concluir quê:
a) 0 = −18 + (alfa)" ⋅ 390(beta)" I
−16 = −18 + (alfa)" ⋅ 3270(beta)" II
Da equação I:
(alfa)" =
Substituindo (alfa)" em II:
2 = 3270(beta)" ⇒ = 3180(beta)" ⇒
⇒ 3−2 = 3180(beta)" ⇒ (beta)" =
Substituindo (beta)" na equação (I):
(alfa)" = = = 54
b) Com (alfa)" = 54 e (beta)" = , a tempera-túra do congelador deve sêr °C maior, ou seja, TA + Logo:
T(t) = TA + ⇒
⇒ TA + (alfa)" ⋅ 3(beta)"t = TA + ⇒
⇒ (alfa)" ⋅ 3(beta)"t = ⇒ 54 ⋅ = ⇒
⇒ ⇒ = 3−4 ⇒ = −4 ⇒ t = 360
Portanto, a tempera-túra é °C maior quê a tempera-túra do ambiente após 360 minutos.
18. Considerando quê a quantidade inicial será dada em t = 0, temos quê f(0) =
= c30 ⇒ f(0) = c.
Como a quantidade inicial é igual à constante c, para determinar o valor de t quê faz com quê essa quantidade de bactérias seja multiplicada por nove, precisamos encontrar t tal quê:
f(t) = 9c ⇒ c32t = 9c ⇒ 32t = 9 ⇒
⇒ 32t = 32 ⇒ t = 1
Resposta: alternativa a.
19. Como o ponto A pertence à função f(x), temos:
f(5) = 25 − k ⇒ 4 = 25 − k ⇒ 22 = 2 5 − k ⇔
⇔ 2 = 5 − k ⇒ k = 3
Como o ponto B pertence à função g(x), temos:
g(2) = k ⋅ 2 + c ⇒ 4 = 2k + c
Como k = 3:
4 = 2 ⋅ 3 + c ⇒ 4 = 6 + c ⇒ c = −2
Com os valores de k e c foram determinados, é possível calcular f(k) + g(1):
2k − k + 3 ⋅ 1 − 2 = 20 + 3 − 2 =
= 1 + 3 − 2 = 2
Resposta: alternativa b.
Página trezentos e noventa e dois
20. Para encontrar o fóssil mais antigo é necessário determinar o maior valor de t utilizando os valores apresentados na tabéla na função Q(t) = Q0 ⋅ .
De acôr-do com a tabéla, temos:
Fóssil 1:
Q0 = 128 e Q(t) = 32
32 = 128 ⋅ ⇒ = ⇒
⇒ = = ⇒ 2−3 = ⇔
⇔ −3 = ⇒ t = (3 ⋅ 5.730)
Fóssil 2:
Q0 = 256 e Q(t) = 8
8 = 256 ⋅ ⇒ = ⇒
⇒ = ⇒ 2−5 = ⇔
⇔ −5 = ⇒ t = (5 ⋅ 5.730)
Fóssil 3:
Q0 = 512 e Q(t) = 64
64 = 512 ⋅ ⇒ = ⇒
⇒ = ⇒ 2−3 = ⇔
⇔ −3 = ⇒ t = (3 ⋅ 5.730)
Fóssil 4:
Q0 = 1.024 e Q(t) = 512
512 = 1.024 ⋅ ⇒ = ⇒
⇒ = ⇒ 2−1 = ⇔
⇔ −1 = ⇒ t = (1 ⋅ 5.730)
Fóssil 5:
Q0 = 2.048 e Q(t) = 128
128 = 2.048 ⋅ ⇒ = ⇒
⇒ = ⇒2−4 = ⇔
⇔ −4 = ⇒ t = (4 ⋅ 5.730)
Logo, o fóssil mais antigo é o 2, com 5 ⋅ 5.730 anos.
Resposta: alternativa b.
Capítulo 6 • Grandezas e medidas
Atividades
1. A unidade de comprimento no SI é o métro. Milha, pé, polegada e jarda são unidades de comprimento do sistema imperial de medidas. Resposta: alternativa b.
2. 8 m = 80 dm = 800 cm Resposta: alternativa c.
3. 0,2 μm = 0,2 × 10−3 mm = 2 × 10−4 mm Resposta: alternativa c.
4. a) Grama (g) e kilograma (kg) – unidades de medida de massa; litro (L) – unidade de medida de volume.
b) Temos quê 1 L = 0,001 m3 = 1 dm3.
Logo, 1,5 L = 0,0015 m3 = 1,5 dm3.
c) A unidade de base de massa no SI é o kilograma (kg). Temos: Quantidade de ouro:
60 g = 60 ⋅ 10−3 kg = 0,06 kg.
A quantidade de minerais (1,5 kg) já está expressa em uma unidade de base do SI.
5. A próxima hora seguidinha é 23:45. De 12:34 até 23:45 se passaram 11 horas e 11 minutos, o quê equivale a:
11 ⋅ 60 min + 11 min = 671 min Resposta: alternativa a.
6. Com 2 kg (ou 2.000 g) de chocolate, é possível fazer ≃ 58,8 bôm-bôns.
Com 1 L (ou 1.000 mL) de creme de leite, é possível fazer ≃ 83,3 bôm-bôns.
Como são necessários ambos os ingredientes para fazer a receita, a quantidade mássima de bôm-bôns quê póde sêr feita é 58.
Resposta: alternativa c.
7. 2t − 920 kg = 2.000 kg − 920 kg = 1.080 kg Portanto, ainda faltam sêr carregados 1.080 kg.
Resposta: alternativa b.
8.
a) 15.000 cm2 = 15.000 ⋅ 10−4 m2 = 1,5 m2
b) 5 m3 = 5 ⋅ 1.000 L = 5.000 L
c) 0,003 km2 = 3 ⋅ 10−3 km2 =
= 3 ⋅ 10−3 ⋅ 1010 cm2 = 3 ⋅ 107 cm2
d) 2.500 mL = 2,5 ⋅ 103 mL = 2,5 ⋅ 1 L =
= 2,5 ⋅ 10−3 m3
9. A ponta da tampa da caneta está entre os valores 11 cm e 12 cm, mais perto de 12 cm quê de 11 cm. Assim, a medida do comprimento da caneta está mais próxima de 11,6 cm.
Resposta: alternativa c.
10. O comprimento de 11,6 cm da caneta possui 3 algarismos significativos, dois dêêsses são certos (1 e 1) e o outro é duvidoso (6).
11. 1,50 m − 800 mm =
= 150 cm − 80 cm = 70 cm Resposta: alternativa a.
12. 16 onças = 1 libra ⇒ 1 onça = libras x = 0,4 ⋅ onças = 0,4 ⋅ libras =
= 0,025 libras Resposta: alternativa c.
13. 1 cm/min = = =
= 10−2 × 60−1 m/s Resposta: alternativa b.
14. Sabemos quê 400 t = 400 ⋅ 103 kg =
= 400 ⋅ 103 ⋅ 103 g. Logo:
d = ⇒ 0,8 g/cm3 = ⇒
⇒ V = ⇒
⇒ V = 500 ⋅ 106 cm3 = 500 m3
Portanto, o volume de petróleo é 500 m³.
15. Temos quê 2 kg = 2.000 g e 0,5 L = 0,5 dm3 = 500 cm3.
Portanto, a densidade d do tijolo é de:
d = = 4 g/cm3
Resposta: alternativa c.
16. A massa (m) de uma fô-lha de papel A4, em grama, é de:
d = ⇒75 = ⇒ m = 4,65
Assim, a massa de papel quê um pé de eucalipto rende é igual a:
20.000 ⋅ 4,65 g = 93.000 g = 93 kg
Resposta: alternativa e.
17. Seja x o número de habitantes dêste município em 2022.
3,5 hab./km2 = ⇒
⇒ x = 1.150 ⋅ 3,5 hab. ⇒
⇒ x = 4.025 hab.
Logo, o número total de habitantes no município em 2022, de acôr-do com o hí bê gê hé, é um número entre 4.000 e 4.100 pessoas.
Resposta: alternativa e.
18. Habitantes da zona rural:
40% ⋅ 30.000 hab. = 12.000 hab.
Área da zona rural:
60% ⋅ 250 km2 = 150 km2
Densidade demográfica da zona rural:
= 80 hab. /km2
Resposta: alternativa a.
19. Calculando a densidade demográfica dos cinco locais, obtemos:
Densidade demográfica de Malta:
≃ 1.333,33 hab. /km2
Densidade demográfica do Brasil:
≃22,22 hab. /km2
Densidade demográfica do México:
=60 hab. /km2
Densidade demográfica da Namíbia:
≃ 2,44 hab. /km2
Densidade demográfica da Ilha Norfolk:
=52,6 hab. /km2
Dos cinco locais, o mais densamente povoado é Malta.
Resposta: alternativa a.
20. Resposta pessoal. Exemplo de resposta: Um liquidificador de potência 550 W foi utilizado durante 12 h em um mês. Na conta de luz, quanto foi cobrado pelo uso do liquidificador, sabendo quê o valor cobrado por kWh é R$ 0,53?
Página trezentos e noventa e três
21. Ano-luz é uma unidade de medida de comprimento; atmosféra é uma unidade de medida de pressão; tesla é uma unidade de medida de intensidade de campo magnético; watt é uma unidade de medida de potência; e hertz é uma unidade de medida de freqüência.
Resposta: alternativa a.
22. 4,4 anos-luz = 4,4 ⋅ 9,5 × 1015 m =
= 41,8 × 1015 m = 4,18 × 1016 m =
= 4,18 × 1013 km ≃ 4,2 × 1013 km Resposta: alternativa b.
23. 1,496 ⋅ 102 milhões de kilometros =
= 1,496 ⋅ 102 ⋅ 106 km =
= 1,496 ⋅ 102 ⋅ 106 ⋅ 103 m = 1,496 ⋅ 1011 m Resposta: alternativa e.
24. 240.000 ha = 2,4 ⋅ 105 ha =
= 2,4 ⋅ 105 hm2 = 2,4 ⋅ 105 ⋅ 10−2 km2 =
= 2,4 ⋅ 103 km2 = 2.400 km2
25. 5 alqueires paulistas = 5 ⋅ 2,42 ha = 12,1 há
O número de sacas quê o Sr. João espera côlher é próximo de:
48 ⋅ 12,1 = 580,8 ≃ 580.
Resposta: alternativa b.
26. 80 GBFabricante = 75 GBUsuário ⇒
⇒ 1 GBF = GBU
500 GBF = 500 ⋅ GBU =
=468,75 GBU ≃468 GBU
Resposta: alternativa a.
27. Área do terreno para venda:
3 ha − 0,9 ha = 2,1 ha = 21.000 m2
Número de terrenos a serem vendidos:
21.000 m2 ∶ 300 m2 = 70
O fazendeiro venderá 20 terrenos por
R$ 20.000,00 cada um e 50 terrenos por
R$ 30.000,00 cada um, o quê totaliza:
R$ 400.000,00 + R$ 1.500.000,00 =
= R$ 1.900.000,00.
Resposta: alternativa c.
28. Sabemos quê 211 = 2.048 e 212 = 4.096.
Assim, para quê um byte seja capaz de representar pelo menos 2.560 informações distintas, o número de bits em um byte deve passar de 8 para 12.
Resposta: alternativa b.
29. Sabemos as seguintes equivalências:
4,8 GB = 4,8 ⋅ 210 MB = 4,8 ⋅ 210 ⋅ 8 megabits
= 39.321,6 megabits
16 min = 16 ⋅ 60 s = 960 s Logo, a taxa de transferência de dáum-lôude póde sêr expressa por:
= 40,96 Mbps
Atividades complementares
1. Metro é uma unidade de medida de comprimento; nílton é uma unidade de medida de fôrça; segundo é uma unidade de medida de tempo; volt é uma unidade de medida de tensão elétrica; e kelvin é uma unidade de medida de tempera-túra.
Resposta: alternativa c.
2. 1,5 m + 18 mm + 1 m =
= 1,5 m + 0,018 m + 1 m = 2,518m
Resposta: alternativa d.
3. 2.500 polegadas = 2.500 ⋅ 2,54 cm =
= 6.350 cm = 63,5 m Portanto, um quarteirão quê tem 2.500 polegadas de comprimento tem como correspondente uma medida entre 50 metros e 100 metros.
Resposta: alternativa c.
4. 50 mi = 50 ⋅ 1.610 m = 50 ⋅ 1,610 km =
= 80,5 km Assim, desprezando as casas decimais, o valor quê deveria estar escrito na placa seria 80 km.
Resposta: alternativa c.
5. Temos quê 3 pés = 0,9144 m.
Logo, 1 pé = 0,3048 m = 30,48 cm.
Além díssu, 1 polegada = 2,54 cm.
Assim, para saber quantas polegadas equivalem a um pé, faz-se a divisão:
30,48 cm ∶ 2,54 cm = 12.
Portanto, um pé equivale a 12 polegadas.
Resposta: alternativa d.
6. 1.000 min = 16h40min
14h15min + 16h40min = 30h55min =
= 24h + 6h55min
Portanto, o relógio irá marcar 6h55min.
Resposta: alternativa d.
7. A massa de todos os livros da tabéla, em kg, é: Matemática:
330 ⋅ 2.100 dg = 330 ⋅ 0,21 kg = 69,3 kg
Ciências naturais:
390 ⋅ 0,280 kg = 109,2 kg
História:
450 ⋅ 3,15 hg = 450 ⋅ 0,315 = 141,75 kg
Geografia: 510 ⋅ 43,7 dag = 510 ⋅ 0,437 =
= 222,87 kg Logo, a massa total dos livros é de 543,12 kg.
Em cada viagem, a massa de livros quê póde sêr carregada é:
400 kg − 75 kg − 73 kg − 30 kg = 222 kg.
Assim, são necessárias 543,12 ∶ 222 ≃ 2,446
viagens para carregar todos os livros.
Como essa quantidade deve sêr um número inteiro, são necessárias pelo menos 3 viagens para finalizar a tarefa.
Resposta: alternativa c.
8. 4 dag = 4 ⋅ 10 g = 4 ⋅ 10 ⋅ 1.000 mg =
= 40.000 mg = 40.000 ⋅ 1 mg
Logo, em um recipiente de 4 dag, há 40.000 doses de 1 mg.
Resposta: alternativa a.
9. Volume de leite:
4 m3 = 4.000 L = 4.000 ⋅ 1.000 mL
Volume de leite em cada embalagem:
(4.000 ⋅ 1.000 mL) ∶ (4.000) = 1.000 mL
Resposta: alternativa e.
10. = = = 102 = 100
Resposta: alternativa d.
11. 36 km/h = = =
=
= 10 m/s Resposta: alternativa d.
12. 1 attosegundo = 10−9 ⋅ 10−9 s = 10−18s
1 femtosegundo = 10−6 ⋅ 10−9 s =
= 10−15 s = 103 ⋅ 10−18 s =
= 103 attosegundos Portanto, 200 femtosegundos =
= 200 ⋅ 103 attosengundos =
= 200.000 attosengundos.
Resposta: alternativa c.
13. Seja x o número de habitantes desta cidade em 2018.
4.406, 96 hab./km2 = ⇒
⇒ x = 435 ⋅ 4.406,96 hab. =
= 1.917.027,6 ≃ 1.917.027 hab.
Resposta: alternativa c.
14. Com o novo televisor, a economia em energia elétrica por hora é de 100 W − 60 W = 40 W. Além díssu, considerando um uso diário de 5 horas do novo aparelho, durante 30 dias de um mês, calcula-se a economia mensal:
5h ⋅ 30 ⋅ 40 W = 6.000 Wh = 6 kWh =
= 6 ⋅ R$ 0,50 = R$ 3,00
Logo, a quantidade necessária de meses para cobrir o valor pago pelo televisor é de:
R$ 1.200 ∶ R$ 3,00 = 400 meses.
Resposta: alternativa b.
Capítulo 7
• Proporcionalidade e semelhança
Atividades
1. Como as duas medidas, a altura da pessoa e a medida da sombra, já estão em métro:
2. a) Sim, pois:
b) Pelas informações do enunciado, pode-se calcular:
⇒ y = = 6,75
⇒ x = = 4,5
3. Segundo o esquema do enunciado, como há um feixe de retas paralelas cortadas por duas transversais:
⇒ ⇒ AM = 37,5
⇒ ⇒ BC = 128
Portanto, BC = 128 m e AM = 37,5 m.
Página trezentos e noventa e quatro
4. Considerando as informações fornecidas pelo enunciado:
⇒ ⇒
⇒ 30(x + 3) = 40(x − 2)
30x + 90 = 40x − 80 ⇒ x = 17
Portanto:
AB = x + 3 ⇒ AB = 17 + 3 = 20
cê dê = x − 2 ⇒ cê dê = 17 − 2 = 15
AB = 20 cm e cê dê = 15 cm.
5.
a) Não, pois, para resolver o problema, é necessário estabelecer uma razão entre as retas r e s e, para isso, são necessárias medidas correspondentes em ambas as retas, o quê não ocorre na reta s.
b) Para resolver a atividade, é necessário saber a medida de , ou .
6. Considerando as informações fornecidas pelo enunciado:
Adicionando as duas equações: AB = 7.
Substituindo esse resultado em qualquer uma das equações do sistema: cê dê = 5.
Ainda utilizando as informações do enunciado: EF = 3GH − 2.
Considerando GH = x:
⇒ = ⇒
⇒ 7x = 5(3x − 2) ⇒ 7x = 15x − 10 ⇒
⇒ x = 1,25
Logo, EF = 3 ⋅ 1,25 − 2 = 1,75.
Então, AB + cê dê + EF + GH =
= 7 + 5 + 1,75 + 1,25 = 15.
7. a) Sim, está correta, pois, FH − 30 = FG, quê é correspondente ao lado MN quê méde 40.
b) Sim, pois a proporção apresenta apenas uma incógnita e, portanto, póde sêr calculada.
c) Sim. Uma possibilidade é .
8. Estabelecendo uma relação de proporcionalidade entre os termômetros:
⇒
⇒ 180 tC = 100 (tF − 32) ⇒
⇒ tC = (tF − 32)
Portanto, considerando a tempera-túra da foto:
tC = (tF − 32) ⇒
⇒ tC = (100,9 −32) ≃ 38,28 ⇒
⇒ tC ≃ 38,28°C
9. Para quê dois polígonos sêjam semelhantes, é necessário quê os ângulos internos correspondentes sêjam congruentes e os lados correspondentes, proporcionais. Em um paralelogramo, os ângulos adjacentes são suplementares, portanto os ângulos internos correspondentes dos paralelogramos são congruentes. Verificando a proporcionalidade dos lados correspondentes:
Portanto, os paralelogramos são semelhantes.
10. Como o lado correspondente de é , conclui-se:
⇒ 3MN = 30 ⇒ MN = 10
11. Alternativa a: falsa, pois não basta ter só os ângulos congruentes, dois a dois. Além díssu, os lados também devem sêr proporcionais, dois a dois. Alternativa b: falsa, pois não basta ter só os lados proporcionais, dois a dois. Além díssu, os ângulos também devem sêr congruentes, dois a dois. Alternativa c: falsa, pois, por exemplo, um losango não é semelhante a um retângulo não quadrado. Alternativa e: falsa, pois a soma de um triângulo e um quadrado podem sêr obtidas pela expressão (n − 2) ⋅ 180, por exemplo. Resposta: alternativa d.
12. Como os decágonos regulares são semelhantes, pode-se afirmar quê = , em quê l2 representa o lado do polígono de maior lado. Diante dessa informação pode-se concluir:
⇒ ⇒
⇒ P1 = = 432
Portanto, o perímetro do polígono menor é 432 mm.
Assim, o lado do menor decágono será:
I1 = = 43, 2
Ou seja, I1 = 43,2 mm ou 4,32 cm.
13. A partir dos dados fornecidos pelo enunciado, pode-se construir a seguinte ilustração:

Como a razão de semelhança entre o tampo maior e o menor é 1,5:
= = 1,5
Logo:
x = 2,5 ⋅ 1,5 = 3,75
y = 3,5 ⋅ 1,5 = 5,25
Calculando o perímetro do tampo maior, obtemos:
P = 2 ⋅ 3,75 + 2 ⋅ 5,25 = 18 ⇒ P = 18
Portanto, o perímetro é 18 m.
14. Resposta pessoal. Exemplos de perguntas:
1. Qual é a razão de semelhança entre os trapézios ABCD e MNPQ?
Como os lados e são correspondentes, pois são a base menor de ambos os trapézios, pode-se responder:
2. Qual é a medida do lado MN?
Como já se sabe a razão de proporcionalidade entre os trapézios e o lado correspondente de é , pode-se responder:
⇒ ⇒ MN =
15. Considerando os dados fornecidos pelo enunciado, pode-se elaborar o seguinte esquema:
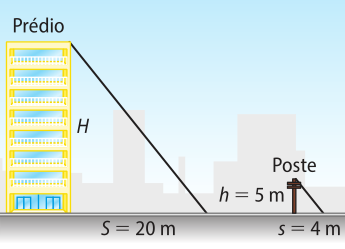
Como os triângulos são semelhantes:
⇒ ⇒ H = 25
Resposta: alternativa a.
16. Considerando as informações fornecidas pelo enunciado:
≃ (J é o ponto médio do segmento ET)
≃ (são ângulos opostos pelo vértice)
≃ (J é o ponto médio do segmento SP)
Disso, temos quê os pontos ESTP formam um paralelogramo, pois as diagonais dêêsse paralelogramo e intersectam-se em seus pontos médios quê é o ponto C. Logo, // . Daí, vêm:
≃ e ≃ JT. Assim, os triângulos
e são semelhantes pelo caso AA de razão igual a 1. Isto é, são congruentes.
2x + 7 = 21 ⇒ x = 7
Encontrando o valor de x e sabendo quê os lados e são congruentes, pode-se afirmar quê a distância quê Júlia deverá percorrer até o parque saindo de sua casa será de 7 km.
17. Sabendo quê e são paralelos, verifica-se quê os triângulos APB e CPD são semelhantes; logo:
⇒ ⇒
⇒ 5 ⋅ cê dê = 36 ⋅ 40 ⇒ cê dê = 288
O comprimento da lagoa é 288 metros.
Resposta: alternativa c.
Página trezentos e noventa e cinco
18. Considere a figura para a resolução. Seja (éli)" o lado do quadrado, logo BE =
= 5 − (éli)".
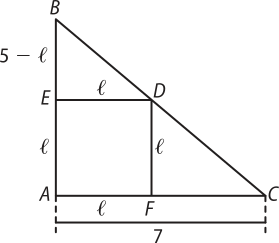
Os triângulos ABC e EBD são semelhantes pelo caso AA, pois eles têm o ângulo do vértice B em comum e ambos têm um ângulo reto. Daí, obtemos a seguinte proporção:
⇒ = ⇒
⇒ 5(éli)" = 7 ⋅ (5 − (éli)") ⇒ 5(éli)" = 35 − 7(éli)" ⇒
⇒ 12(éli)" = 35 ⇒(éli)" =
Portanto, o lado do quadrado méde cm.
Resposta: alternativa c.
19. Como a mesa tem comprimento igual a 2 metros, QL = 2 m − 1,2 m = 0,8 m.
Seja o ponto C o vértice do ângulo reto do triângulo retângulo em quê a hipotenusa é o segmento . Assim,
(triângulo)"LCB ∼(triângulo)"LQP pelo caso AA. Daí, temos a seguinte proporção:
⇒ ⇒
⇒QP = ≃ 0,67
QP ≃ 0,67 m = 67 cm Resposta: alternativa a.
20. Para determinar a área do retângulo ABCD, devemos obtêr as medidas de BC e cê dê. Como segue:
BC = BE − CE = 15 − 6 = 9
Logo, BC = 9 cm.
Os triângulos BCQ e BEF são semelhantes pelo caso AA, pois eles têm o ângulo do vértice B em comum e ambos têm dois ângulos rétos. Disso podemos obtêr a seguinte proporção: . Daí, temos:
⇒ CQ = ⇒ CQ = 4,8
E como cê dê = CQ + QD = 4,8 + 1,2 = 6,
cê dê = 6.
Portanto, a área do retângulo ABCD é igual a 6 cm ⋅ 9 cm = 54 cm2.
Resposta: alternativa b.
21. a) Considerando os dados fornecidos pelo enunciado, pode-se elaborar a seguinte ilustração:
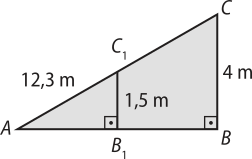
b) Como os triângulos AB1C1 e ABC são semelhantes e considerando quê CC1 = x, conclui-se:
⇒ 12,3 + x = x = 32,8 − 12,3 ⇒ x = 20,5
A pessoa deve caminhar 20,5 m.
22. 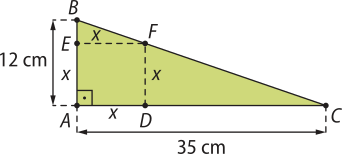
Sejam e os catetos do triângulo retângulo e AEFD o quadrado quê será extraído. Pelo caso AA, (triângulo)"ABC ∼(triângulo)"EBF, daí, tem-se:
⇒ ⇒ x =
Como ≃ 8,94, a medida do lado do quadrado desejado pelo marceneiro está mais próxima de 9 cm.
Resposta: alternativa c.
23. Pelo caso AA, (triângulo)"AEC ∼(triângulo)"DEB, pois os ângulos do vértice E são opostos pelo vértice e os ângulos e ; e e des ses triângulos são alternos internos, portanto, congruentes. Disso, obtemos a seguinte proporção:
⇒ ⇒AE = DE
Temos também quê (triângulo)"AEF ∼(triângulo)"ADB pelo caso AA, pois ambos têm um ângulo reto e o ângulo do vértice A em comum. Disso, temos a seguinte proporção:
Como AD = AE + DE, temos:
Como estudamos anteriormente quê
AE = DE, temos:
⇒ ⇒
⇒ ⇒ ⇒EF = EF = 2,4
Portanto, o comprimento da hás-te deve ter 2,4 metros.
Resposta: alternativa c.
24. Sejam x, y, z lados do triângulo semelhante respectivos aos lados 10, 12, 18:
Como o perímetro dos triângulos é 40 cm e 60 cm:
⇒ x = 15
⇒ y = 18
⇒ z = 27
Os lados do triângulo semelhantes têm medida 15 cm, 18 cm e 27 cm.
• Resposta pessoal. Exemplo de atividade: Os lados de um triângulo médem 4 cm, 5 cm e 6 cm. Determine as medidas dos lados de um triângulo semelhante ao anterior cujo perímetro é 45 cm.
Sejam x, y, z lados do triângulo semelhante respectivos aos lados 4, 5, 6:
Como os triângulos têm perímetro 15 cm e 45 cm:
⇒ x = 12
⇒ y = 15
⇒ z =18
Os lados do triângulo semelhante têm medida 12 cm, 15 cm e 18 cm.
25. O corrimão é formado por duas partes horizontais de 30 cm cada uma e por uma parte inclinada, quê corresponde à hipotenusa de um triângulo retângulo cujos catetos médem 90 cm e 120 cm (5 degraus com 24 cm cada um).
Com base nesses dados, a medida (C) do corrimão será:
C = 30 + 30 + =
= 60 + =
= 60 + = 60 + 150 = 210
O corrimão méde 210 cm ou 2,10 m.
Resposta: alternativa d.
26. De acôr-do com a ilustração fornecida pelo enunciado e aplicando as relações métricas do triângulo retângulo, temos:
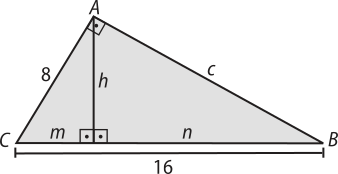
As medidas são: , , e
27. De acôr-do com o enunciado, pode-se obtêr a ilustração a seguir:

Aplicando o teorema de Pitágoras:
(x + 8)2 = x2 + 162
x2 + 16x + 64 = x2 + 256
16x = 256 − 64 ⇒ x = 12
AC = x + 8
AC = 12 + 8 = 20
Logo, a hipotenusa méde 20 m.
Página trezentos e noventa e seis
28. Não. Como a altura é relativa à hipotenusa, não é possível calcular as medidas dos catetos. Para sêr possível calcular, seria necessário mais uma informação, por exemplo: a medida de uma das projeções.
29. Considerando as informações do enunciado, pode-se elaborar a imagem a seguir:
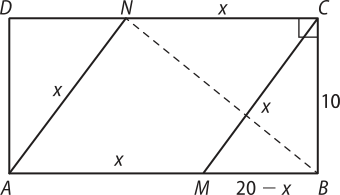
Por meio do triângulo BCM, quê é retângulo em B, pode-se estabelecer a seguinte relação:
x2 = (20 − x)2 + 102 ⇒
⇒ x2 = 400 − 40x + x2 + 100 ⇒
⇒ 40x = 500 ⇒ x=
Portanto, para calcular a medida NB, pode-se considerar o triângulo retângulo BCN. Assim:
NB2 = x2 + 102 ⇒ NB2 = + 102 ⇒
⇒ NB2 = ⇒
⇒ NB = = ≃16
30. Observando a sequência, os quadrados representados pelas 4ª, 11ª e n ª figuras correspondem aos números inteiros 52, 122 e x2, em quê x = n −1.
Como x precisa sêr o maior número, conclui-se:
x2 = 52 + 122 ⇒ x2 = 169 ⇒ x = 13
Portanto, será a 12ª figura.
Resposta: alternativa b.
31. Como o trecho RS méde 1.700 m, então o trecho ST méde 300 m.
Assim, considerando o triângulo STU, quê é retângulo em T, tem-se quê ST = 300, TU = 400 e US = x. Portanto:
US2 = ST2 + TU2 ⇒
⇒ x2 = 3002 + 4002 ⇒ x = 500
Assim, o custo de instalação será:
Tubulação através do rio:
500 ⋅ 830 = 415.000
Tubulação terrestre:
1.700 ⋅ 400 = 680.000
Custo total:
415.000 + 680.000 = 1.095.000
Resposta: alternativa d.
32. Em qualquer triângulo retângulo, o produto das medidas dos catetos é igual ao produto da medida da hipotenusa pela medida da altura relativa à hipotenusa. Daí, temos:
196H = 84 ⋅ 140
H =
H = 60
Portanto, a altura H do drone em relação ao solo é igual a 60 metros.
Resposta: alternativa d.
33. Resposta pessoal. Exemplo de pergunta: No triângulo retângulo a seguir, quais são as medidas a, b e h?

Da figura, tem-se:
a = 50 − 18 ⇒ a = 32
Pelo teorema de Pitágoras, tem-se:
502 = b2 + 402 ⇒ 2.500 = b2 + 1.600 ⇒
⇒ b2 = 900 ⇒ b = 30
E, pela relação h2 = m ⋅ n, tem-se:
h2 = 18 ⋅ 32 ⇒ h = 24
Atividades complementares
1. Considerando y como a altura do compartimento do meio, pode-se escrever a seguinte relação:
= ⇒ 2y = 42 ⇒ y = 21
Resposta: alternativa d.
2. Considerando a medida da pessoa e da árvore, em centímetro, pode-se calcular o comprimento da sombra da árvore.
Observe a ilustração:
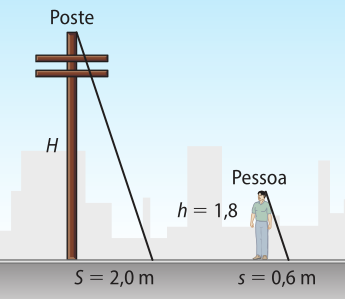
⇒ ⇒ 0,6 H = 3,6 ⇒
⇒ H = 6,0
Após a sombra do poste diminuir 0,50 m, a sombra da pessoa será:
⇒ ⇒
⇒ ⇒ 6,0t = 2,7 ⇒ t = 0,45
A sombra será de 0,45 m ou 45 cm.
Resposta: alternativa b.
3. Como a altura do poste e de Ana são proporcionais às medidas de suas respectivas sombras, então:
⇒ x = 2,3
Resposta: alternativa b.
4. Pelo esquema e pêlos dados fornecidos no enunciado, conclui-se quê:
MB = 10, pois MN = 16 e BN = 6
Assim, pode-se estabelecer a seguinte relação:
⇒ ⇒ AB = 15
Outra informação quê se póde obtêr é:
BD = 19, pois BC = 9 e cê dê = 10
Assim, pode-se estabelecer a seguinte relação:
⇒ ⇒
⇒ 2m + 10 = 19 ⇒ m = 4,5
Por fim, tem-se:
⇒ ⇒
⇒ FG = ⇒ FG = 7,5
Como FG = 7,5 e GH = 4,5, tem-se quê FH = 12.
Portanto, AB + FH = 15 + 12 = 27, ou seja, divisível por 3.
Resposta: alternativa a.
5. Pelo enunciado é possível estabelecer as relações:
⇒ ⇒
⇒ A(minutos)"B(minutos)" = = 60
⇒ ⇒
⇒ C(minutos)"D(minutos)" = = 30
Portanto, A(minutos)"B(minutos)" − C(minutos)"D(minutos)" = 60 − 30 = 30.
Resposta: alternativa b.
6.
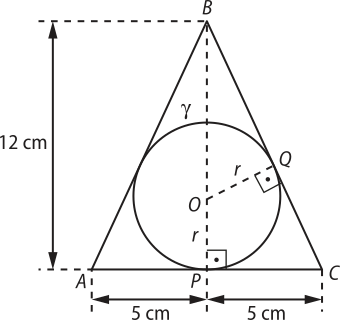
Utilizando o teorema de Pitágoras no triângulo BPC, tem-se:
BC2 = BP2 + CP2 ⇒
⇒ BC2 = 122 + 52 ⇒
⇒ BC2 = 144 + 25 ⇒
⇒ BC2 = 169 ⇒ BC = 13
Pelo caso AA, os triângulos BOQ e BPC
são semelhantes, obtendo-se:
⇒ 13R = 60 − 5R ⇒
⇒ 18R = 60 ⇒ R =
Resposta: alternativa d.
7. Considerando as informações do enunciado, pode-se elaborar a seguinte ilustração:
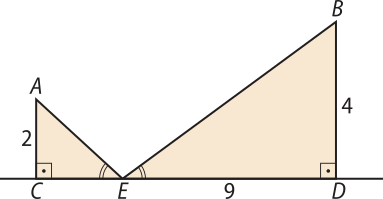
Portanto, pode-se afirmar quê:
(triângulo)"ACE ∼ (triângulo)"BDE
Página trezentos e noventa e sete
Como os triângulos são semelhantes, conclui-se:
⇒ ⇒ CE = 3
Resposta: alternativa a.
8. Como o trajeto é formado por três segmentos quê formam um percurso fechado, conclui-se quê esse trajeto é um triângulo.
Após andar 30 cm, a instrução II pede para realizar um giro de 90°, portanto esse triângulo é retângulo.
A instrução IV, quê pede para voltar ao ponto inicial, representa a construção da hipotenusa do triângulo, pois é oposta ao ângulo de 90°, ou seja, as instruções I e III formam os catetos do triângulo retângulo. Assim, nomeando a hipotenusa dêêsse triângulo como x:
x2 = 302 + 402 ⇒ x = 50
Portanto, o trajeto percorrido pelo robô é um triângulo cuja hipotenusa méde 50 cm.
Resposta: alternativa a.
9. Como AD = 2, PM = 2 – x. Temos também quê CP = PM e podemos determinar a medida de pelo teorema de Pitágoras, como segue:
CP2 = PN2 + NC2
CP2 = x2 + 22
CP =
Portanto, para 0 ≤ x ≤ 2,
S(x) = PM + PD + PC =
= (2 − x) + .
Resposta: alternativa e.
10. Pelo enunciado, pode-se obtêr quê:
BC = 2,9 − 1,3 = 1,6
Como r1// r2, segue do teorema de Tales quê vale a relação:
⇒ ⇒ cê dê = 0,6
Resposta: alternativa a.
11. De acôr-do com o enunciado, pode-se concluir quê:
CE = e AF = .
Como AD = BC, pois são os lados opostos de um paralelogramo, pode-se afirmar quê AF = = .
Além díssu, do fato quê e são congruentes e quê é um ângulo em comum nos triângulos GAF e GCE, temos, pelo caso AA (ângulo-ângulo) quê GAF e GCE são semelhantes.
Assim, a razão de semelhança entre os lados correspondentes dos triângulos GCE e GAF é:
Portanto, a razão de semelhança entre as áreas dos triângulos será:
= = 1,265625
Ou seja, a área do triângulo GCE é, aproximadamente, 27% maior quê a área do triângulo GAF.
Resposta: alternativa a.
Capítulo 8
• Trigonometria no triângulo retângulo
Atividades
1. Utilizando as relações trigonométricas apresentadas neste Capítulo, é possível determinar o quê se pede:
a) sen (gama)" = = =
cos (gama)" = = =
tg (gama)" = =
b) sen (beta)" = =
cos (beta)" = =
tg (beta)" = =
2.
a) Tangente. No triângulo retângulo formado, h é a medida do cateto ôpôsto ao ângulo de inclinação e c é a medida do cateto adjacente.
b) Significa quê a razão entre a altura do desnível e o comprimento da projeção da rampa é de .
3. Utilizando a tangente do ângulo formado entre os raios solares e o chão, é possível chegar à seguinte relação: tg 30° = ⇒ 0,58 = ⇒ x = 29
A altura do prédio é aproximadamente 29 m.
4. Pode-se determinar a medida do cateto adjacente por meio do teorema de Pitágoras:
172 = x2 + 152 ⇒ x2 = 64 ⇒ x = 8
Como 8 cm é a medida do menor lado, o ângulo ôpôsto a ele é o menor ângulo.
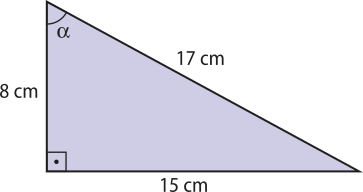
Aplica-se, então, a definição de seno, cosseno e tangente: sen (alfa)" = ; cos (alfa)" = ; tg (alfa)" =
5. Considerando o triângulo retângulo ABD, temos:
tg 50° = 1,19 ⇒ = 1,19 ⇒
⇒ h − 1,6 = 1,19 ⋅ AB (I)
Por outro lado, considere o triângulo ADC. Temos:
tg 41° = 0,87 ⇒ = 0,87 ⇒
⇒ h − 1,6 = 0,87 ⋅ (AB + 20) =
= 0,87 ⋅ AB + 17,4 (II)
De (I) e (II), obtemos:
1,19 ⋅ AB = 0,87 ⋅ AB + 17,4 ⇒
⇒ 0,32 ⋅ AB = 17,4 ⇒ AB = = 54,375
Substituindo o valor de AB em (I), chegamos a:
h − 1,6 = 1,19 ⋅ 54,375 ⇒
⇒ h ≃ 64,71 + 1,6 = 66,31
Portanto, a altura do barranco é aproximadamente 66,31 m.
6. Utilizando o esboço a seguir como referência, tem-se:
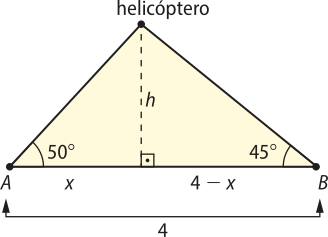
tg 45° = ⇒ 1 = ⇒
⇒ h = 4 − x ⇒ x = 4 − h
Sendo tg 50° = ⇒ 1,19 = ⇒
⇒ 1,19(4 − h) = h ⇒ h ≃ 2,17
A medida h é aproximadamente 2,17 km ou 2.170 m.
7. Relembrando quê velocidade =, para encontrar o tempo solicitado na atividade é necessário determinar a distância x, em métro, percorrida pelo ciclista, no caso, a medida da hipotenusa. Sendo assim:
sen 3° = ⇒ 0, 05 = ⇒
⇒ x= = 600
Com o valor de x já determinado, usar da fórmula da velocidade para obtêr o tempo t, em segundos.
4 = ⇒ t = = 150
Convertendo o tempo para minutos, tem-se t = = 2,5
O tempo quê o ciclista levou para percorrer completamente a rampa foi 2,5 minutos.
Resposta: alternativa a.
8. a) Utilizando a definição das medidas trigonométricas, é possível determinar o valor do cosseno do ângulo a∶
cos (alfa)" = = 0,625. Sendo assim, utiliza-se a função cos−1 da calculadora científica, chegando-se ao valor de (alfa)" ≃ 51°.
b) Seno do ângulo a∶
sen (alfa)" = = 0,333. Utiliza-se, então, a função sen−1 da calculadora científica chegando-se ao valor de (alfa)" ≃ 19°.
Página trezentos e noventa e oito
c) A partir das informações do enunciado, considere a figura a seguir:
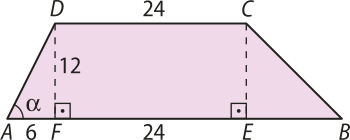
A medida EC = DF = 12. Já a medida AF deve sêr ôbitída subtraindo a medida AE de FE, portanto AF =
= 30 − 24 = 6. Determina-se, então, a tangente de (alfa)": tg (alfa)" = = =2.
Logo, com a função tg−1 da calculadora científica, tem-se quê (alfa)" ≃ 63°.
9. Utilizando a 2ª relação trigonométrica, é possível determinar o quê se pede:
a) cos 25° = sen 65° = 0,90
b) cos 80° = sen 10° = 0,17
c) sen 40° = cos 50° = 0,64
10. Inicialmente, considere o triângulo ABC. Da relação do seno de um ângulo, temos:
sen (alfa)" = 0,8 ⇒ = 0,8 ⇒ AC = 15
Assim, pelo teorema de Pitágoras no triângulo ABD:
(AC)² = (AB)² + (BC)² ⇒
⇒ (BC)² = 225 − 144 ⇒ BC = = 9
Agora, considere o triângulo BDC. Temos sen (alfa)" = 0,8 ⇒ = 0,8 ⇒ BD = 7,2
Aplicando o teorema de Pitágoras no triângulo BDC, obtemos:
(BC)² = (BD)² + (DC)² ⇒
⇒ (DC)² = 81 − 51,84 ⇒
⇒ DC = = 5,4.
Resposta: alternativa a.
11. Como a soma das bases é igual a 30 m e a base maior é o dôbro da menor, pode-se concluir quê a base menor méde 10 m e a base maior, 20 m. Como o ângulo obtuso CA méde 150°, então o ângulo DB méde 30°, pois são suplementares.
Logo:
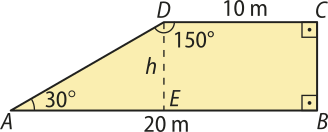
Como sen 30° =
= 0,5 e sen2 30° + cos2 30° = 1, então: cos 30° =
Assim, a altura DE vale: tg 30° = ⇒ ⇒
⇒ h =
A altura do trapézio é m.
12. De acôr-do com o enunciado, podemos construir o seguinte esquema:
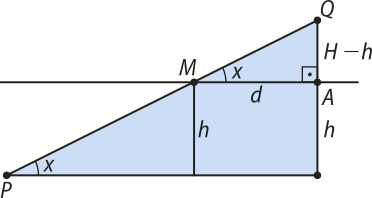
Assim, para determinar a diferença entre as alturas das torres, vamos utilizar o triângulo AQM e calcular a tangente de x:
tg x = ⇒ H − h = d ⋅ tg x
Resposta: alternativa b.
13. Utilizando a representação a seguir como referência, considera-se quê a altura do prédio méde h e a distância quê a pessoa se afastou méde x. Logo:
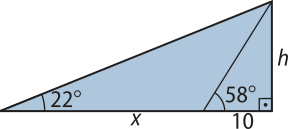
tg 58° = ⇒ 1,6 = ⇒ h = 16
tg 22° = ⇒ tg22° = ⇒
⇒ x + 10 = ⇒ x =30
Portanto, o prédio tem 16 metros de altura, e a pessoa se afastou 30 metros.
14. Como o submarino está a 400 m de profundidade, tem-se: Distância horizontal (x) do submarino A até o barco B: tg 62° = ⇒
⇒ x = tg 62° ⋅ 400=1,9 ⋅ 400 = 760
Distância horizontal (y) do submarino A até o barco C: tg 40° = ⇒
⇒ y = tg 40° ⋅ 400 = 0,8 ⋅ 400 = 320
Portanto, a distância entre os barcos é de 760 m + 320 m = 1.080 m.
15. Resposta pessoal. Exemplo de problema: João e Pedro ganharam um drone de presente e foram ao clube de aeromodelismo fazê-los voar. Porém, para evitar possíveis problemas, o clube instituiu a seguinte regra: a distância mássima entre o drone e seu respectivo proprietário deve sêr de 70 m. Como bons estudantes de Matemática, João e Pedro quiseram verificar se estavam cumprindo a regra. Sendo assim, ambos ficaram parados em um mesmo local, um de costas para o outro, e verificaram quê o equipamento de João pairava a 30 metros do chão, formando um ângulo de 30° entre a altura e suas posições. O equipamento de Pedro também estava a 30 metros do chão, formando um ângulo também de 60° entre a altura e sua posição. Considere quê João e Pedro ocupem o mesmo espaço. Determine se algum dos drones estava ou não cumprindo a regra. Considere cos 30° ≃ 0,87 e cos 60° = 0,5. Elaborando uma ilustração a partir do enunciado do problema, obtém-se quê:
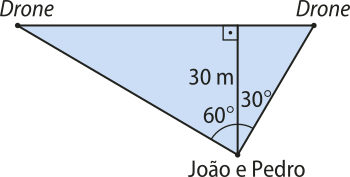
A distância entre João e o drone equivale a hipotenusa no triângulo, quê será definida com x. Logo:
cos 60° = ⇒ x = = 60
A distância entre Pedro e o drone equivale a hipotenusa no triângulo, quê será definida com y. Logo:
cos 30° = ⇒ y = ≃ 34,48
Como as distâncias de João e Pedro são, respectivamente, 60 m e 34,48 m, João e Pedro estão cumprindo a regra do clube.
16. A partir do esquema a seguir, é possível perceber quê o ângulo BC é de 60°.
Sendo assim:
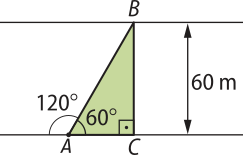
sen 60° = ⇒ ⇒
⇒ AB = 40√ 3
Dessa maneira, a distância percorrida pelo barco é _ m.
17. Utilizando o esquema a seguir como referência, é possível determinar a altura em quê a pessoa se encontra do chão:
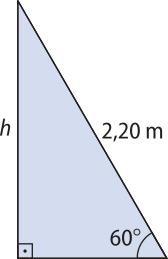
sen 60° = ⇒ = ⇒ h = 1,903
A pessoa estará a 1,903 m do chão.
18. Utilizando a definição de tangente, tem-se:
tg 30° = ⇒
⇒ 0, 58 = ⇒ x = ≃ 20,7
A distância é aproximadamente 20,7 m.
19. Segundo enunciado, sabe-se quê BA =
= 8 m, DA = 4 m e BC = 10 m. Então, considerando-se DE = BF = y e BE = x + 4, como na figura a seguir, tem-se:
Página trezentos e noventa e nove
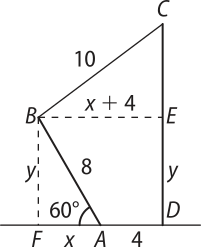
sen 60° = ⇒ y = 8 ⋅ sen 60° ⇒
⇒ y = 8 ⋅ ⇒ y =
cos 60° = ⇒ x = 8 ⋅ cos 60° ⇒
⇒ x = 8 ⋅ ⇒ x = 4
Aplicando o teorema de Pitágoras no triangulo CEB, tem-se:
(BC)2 = (CE)2 + (BE)2 ⇒
⇒ 102 = (CE)2 + 82 ⇒
⇒ (CE)2 = 100 − 64 ⇒ CE = 6
Portanto, a altura do poste é:
cê dê = CE + DE = 6 +
A altura do poste em relação ao solo é (6 + ) m.
20. a) Para determinar a medida CH, em centimetro, basta aplicar a definição de tangente:
tg 30° = ⇒
⇒ CH = 12 ⋅ tg 30° = 12 ⋅ = 4√3
Portanto, a medida de CH é 4√ 3 cm.
b) Calculando a tangente do ângulo BC, tem-se:
tg (alfa)" = = = 1
Portanto, o ângulo solicitado tem medida igual a 45°.
21. Sabendo quê o segmento méde 50 metros, determina-se assim a medida de :
tg 60° = ⇒ AB =
Com a medida AB calculada, determina-se então a medida AD, em métro:
sen 30° = = ⇒ AD =
Resposta: alternativa e.
22. Utilizando o segmento auxiliar , divide-se o quadrilátero nos seguintes triângulos:
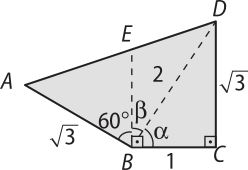
Aplicando o teorema de Pitágoras no (delta)"DCB, obtém-se:
(BD)2 = (BC)2 + (cê dê)2 ⇒ BD = 2
Logo, sen (alfa)" = = . Então:
(alfa)" = 60° ⇒ (beta)" = 30° ⇒ (alfa)" + (beta)" = 90°
Aplicando o teorema de Pitágoras no (delta)"ABD, obtém-se:
(AD)2 = (AB)2 + (BD)2 ⇒
⇒ (AD)2 = 3 + 4 ⇒ AD =
23. Considerando o esquema a seguir, percebe-se quê os ângulos AB e DB médem 15°, portanto o triângulo DAB é isósceles, logo a distância entre as cidades A e B é a mesma quê a distância entre as cidades B e D, ou seja, AB = BD.
Sendo assim, basta determinar a medida de para calcular a distância entre as cidades.
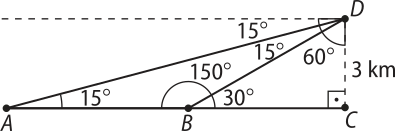
cos 60° = ⇒ BD = = 6
A distância entre as cidades B e D é 6 km.
Resposta: alternativa e.
24. Observando o esquema a seguir, é possível determinar a altura do prédio:
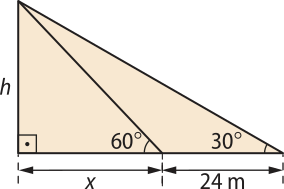
tg 60° = ⇒ ⇒ x = (I)
tg 30° = ⇒ ⇒
⇒ x = − 24 (II)
De (I) e (II), vêm:
= _ − 24 ⇒
⇒ h = 3h − = ⇒
⇒ h =
Logo, a altura do prédio é _ m.
25. Seja h a medida da altura quê procuramos, em métro. De acôr-do com o enunciado, podemos montar um esquema conforme a seguir:
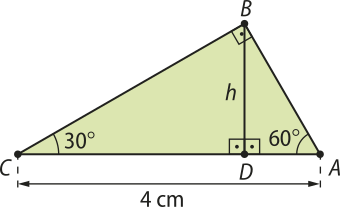
Assim: tg 60° = ⇒ h = AD (I)
tg 30° = ⇒ h = DC (II)
De (I) e (II), vêm:
DC = AD ⇒ DC = 3AD
Por outro lado,
AD + DC = AC = 4 ⇒ 4AD = 4 ⇒ AD = 1
Substituindo o valor de AD em (I), obtemos h = .
Resposta: alternativa c.
26. A partir das informações fornecidas no enunciado, pode-se utilizar o esquema a seguir:
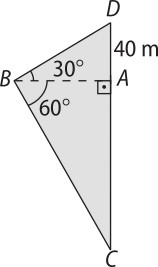
Aplicando a definição de tangente no triângulo BAD, tem-se quê:
tg 30° = ⇒ = ⇒
⇒ AB =
Para obtêr a medida da largura do rio, deve-se determinar a medida AC, quê é um cateto do triângulo BAC. Assim, ao aplicar a definição de tangente, obtém-se quê:
tg 60° = ⇒ = ⇒
⇒AC = ⇒ AC = 120
Assim, a medida de corresponde a 120 m.
27. Seja d a medida da distância entre navio e praia em métro. De acôr-do com o enunciado, podemos montar o seguinte esquema:
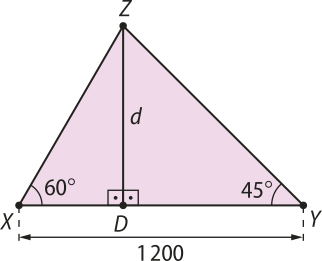
Logo: tg 60° = ⇒ d = XD (I)
tg 45° = ⇒ d = DY (II)
De (I) e (II), vêm:
DY = XD
Por outro lado,
XD + DY = XY = 1.200 ⇒
⇒ XD = 1.200 ⇒
⇒ XD = = 440
Substituindo o valor de XD em (I), obtemos d = = 760.
Resposta: alternativa b.
28. Resposta pessoal. Uma resposta possível: Com a construção de um teodolito, efetuar o cálculo da altura do prédio mais próximo da escola, considerando as medidas realizadas em pelo menos duas posições diferentes.
Página quatrocentos
Atividades complementares
1. Utilizando a definição da tangente nos dois ângulos, tem-se:
⇒
Substituindo o valor de h, da equação (I), na equação (II), obtém-se:
0,36d − 5 = 0,32d ⇒ 0,04d = 5 ⇒ d = 125
Substituindo o valor de d na equação (I), obtém-se:
h = 0,36 ⋅ 125 = 45
Resposta: alternativa d.
2. Por meio do cálculo da tangente, determina-se a altura dos olhos de João até o topo da estátua:
tg 66° = ⇒ h ≃ 36, 94
Logo, a altura da estátua é de 36,94 m + 1,90 m ≃ 38 m Resposta: alternativa e.
3. Por meio das coordenadas dos pontos, considera-se quê x é a distância entre o ponto P e a origem. Logo:
x2 = 152 + 82 ⇒ x = 17
Portanto, sen (alfa)" = .
Resposta: alternativa c.
4. Utilizando a figura a seguir como referência e sabendo quê o ângulo BC = 30°, calcula-se a distância percorrida pelo barco:
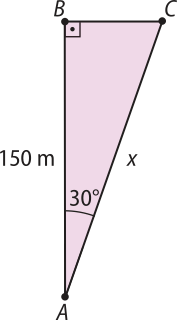
cos 30°= = ⇒
⇒ = 300 ⇒ x = _ =
A distância percorrida pelo barco foi de 100√3 metros.
Resposta: alternativa d.
5. Calculando o seno do ângulo destacado na figura, tem-se:
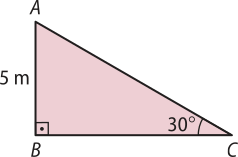
sen 30° = ⇒ ⇒ AC = 10
Logo, o comprimento da esteira rolante é 10 m.
Resposta: alternativa b.
6. Seja c a medida de comprimento do cabo, em métro. Vamos avaliar as três opções de instalação. Para isso, calculamos a tangente do ângulo (alfa)" em cada caso.
Opção 1: sen 30° = ⇒ c = 2 ⋅ 11 = 22
Opção 2: sen 45° = ⇒
⇒ c = 12 ⋅ =
Opção 3: sen 60° = ⇒
⇒ c = 18 ⋅ =
Como , , 22, então a opção escolhida será a opção 2 e a medida de cada cabo terá m.
Resposta: alternativa c.
7. Seja d a medida do comprimento do segmento tracejado, em métro.
Observe quê os segmentos quê representam os comprimentos das vagas de automóveis e da vaga de moto são paralelos.
Assim, de acôr-do com os dados da tabéla, temos o seguinte esquema:
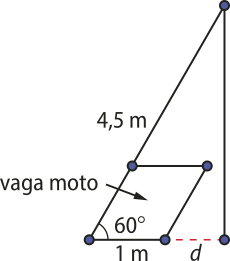
Logo: cos 60° = ⇒ ⇒
⇒ d = 2,25 − 1 ⇒ d = 1,25
Resposta: alternativa c.
8. Utilizando a definição de cosseno e considerando as informações do enunciado, tem-se:
cos 45° = ⇒ AB =
Resposta: alternativa b.
9. Seja x a distância entre a Estação Minizoo e a Estação vista do Céu. Pelo enunciado, tem-se quê:
x + 3x = 480 ⇒ x = 120
Logo, 3x = 360.
Portanto, para determinar a altura da estação vista do Céu, basta adicionar a altura de cada um dos triângulos da figura correspondente à altura da Estação Minizoo (h1)e à diferença entre a altura da Estação vista do Céu e a da Estação Minizoo (h2). Essas alturas podem sêr determinadas da seguinte maneira:
sen 60° = ⇒ h1 = ⋅ 360 =
= ⋅ 360 = 306
sen 30° = ⇒ h2 = ⋅ 120 = 60 ⇒
⇒ h2 = 60
Portanto, em métro, a altura total é h1 + h2 = 366.
Resposta: alternativa c.
10. Aplicando a definição de tangente no triângulo ABE, determina-se o valor de x: tg 30° = ⇒ x =
Aplicando o teorema de Pitágoras, tem-se:
(BE)2 = 62 + ⇒ BE =
Logo, o perímetro do triângulo, em métro, é dado por:
6 + + = 6 + .
Resposta: alternativa c.
11. Seja x a medida do lado do quadrado. Sabendo quê a área do cartão méde 256 cm², então:
x2 = 256 ⇒ x = 16
O lado do cartão méde 16 cm.
Além díssu, sabe-se quê o (triângulo)"APB é retângulo em P, logo:
sen 30° = ⇒ BP = 8
cos 30° = ⇒ AP = 8√3
Portanto, o perímetro do triângulo, em centímetro, é:
16 + 8 + = 8(3 + )
Resposta: alternativa d.
12. Utilizando a figura a seguir como referência, é possível calcular a área da parte de João:

tg 30° = ⇒ ⇒ x =
Assim, a área do terreno de João é, em kilometro quadrado, dada por:
Área total = 3 ⋅ 2 = 6
Como a área total deixada como herança é de 6 km2, tem-se quê a porcentagem do terreno de João equivale a cerca de 19%, pois:
≃ 0,1925 = 19,25%
Resposta: alternativa e.
1 BRASIL. Ministério da Educação. Base Nacional Comum Curricular: educação é a base. Brasília, DF: MÉC, 2018. p. 462. Disponível em: https://livro.pw/asnqu. Acesso em: 11 set. 2024.