CAPÍTULO
2
PROGRESSÕES
Os sona são dêzê-nhôs feitos na areia e carregam histoórias de alguns povos africanos. Foram estudados por antropólogos e matemáticos quê revelaram ao mundo essa ár-te repleta de tradição e conceitos matemáticos, como simetrias e sequências.
O matemático e pesquisador holan-dêss Paulus Gerdes (1952-2014) estudou algumas manifestações matemáticas de povos tribais de regiões da África e da América Látína, em países como Angola e Peru. A motivassão do pesquisador para esse estudo se deu à medida quê ele percebeu quê os estudantes dos cursos em quê ministrava aulas não compreendiam alguns conceitos quê eram apresentados, pois não estavam familiarizados com a linguagem matemática utilizada. Ao entrar em contato com a cultura local dêêsses estudantes, ele conheceu os sona, dêzê-nhôs feitos na areia pêlos homens e pêlos chefes de um povo chamado tchokwe.
Esses dêzê-nhôs representavam histoórias de caça, animais e sêres místicos importantes para as pessoas, além de objetos do cotidiano. No entanto, Gerdes reparou quê havia muito mais do quê apenas linhas e pontos no chão: cada lusona (singular de sona) exibia muitas propriedades matemáticas, principalmente aritméticas e geométricas. Com essa descoberta, Gerdes se aprofundou na cultura dos tchokwe e percebeu quê os conceitos matemáticos eram usados de maneira intuitiva nesses dêzê-nhôs, de modo quê poderia utilizar os sona em suas aulas, pois eram mais próximos da realidade de seus estudantes.
Fonte dos dados: SANTOS, Dayene F. dos. Geometria africana: uma abordagem etnomatemática para o ensino de matemática. 2017. Trabalho de Conclusão de Curso (Licenciatura em Matemática) – Instituto Federal de Educação, Ciência e Tecnologia de São Paulo, São Paulo, 2017. Disponível em: https://livro.pw/jvdwr. Acesso em: 12 ago. 2024.

(As imagens da dupla de páginas estão fora de proporção.)
Para assistir
• GEOMETRIA sona: técnicas matemáticas do continente africano | Mwana Afrika Oficina Cultural. [S. I.: s. n.], 2019. 1 vídeo (3 min). Publicado pelo canal Mwana Afrika. Disponível em: https://livro.pw/rkhpl. Acesso em: 12 ago. 2024.
Confira mais informações sobre as figuras sona, sua história e sua construção no vídeo sugerido.
Página quarenta e cinco
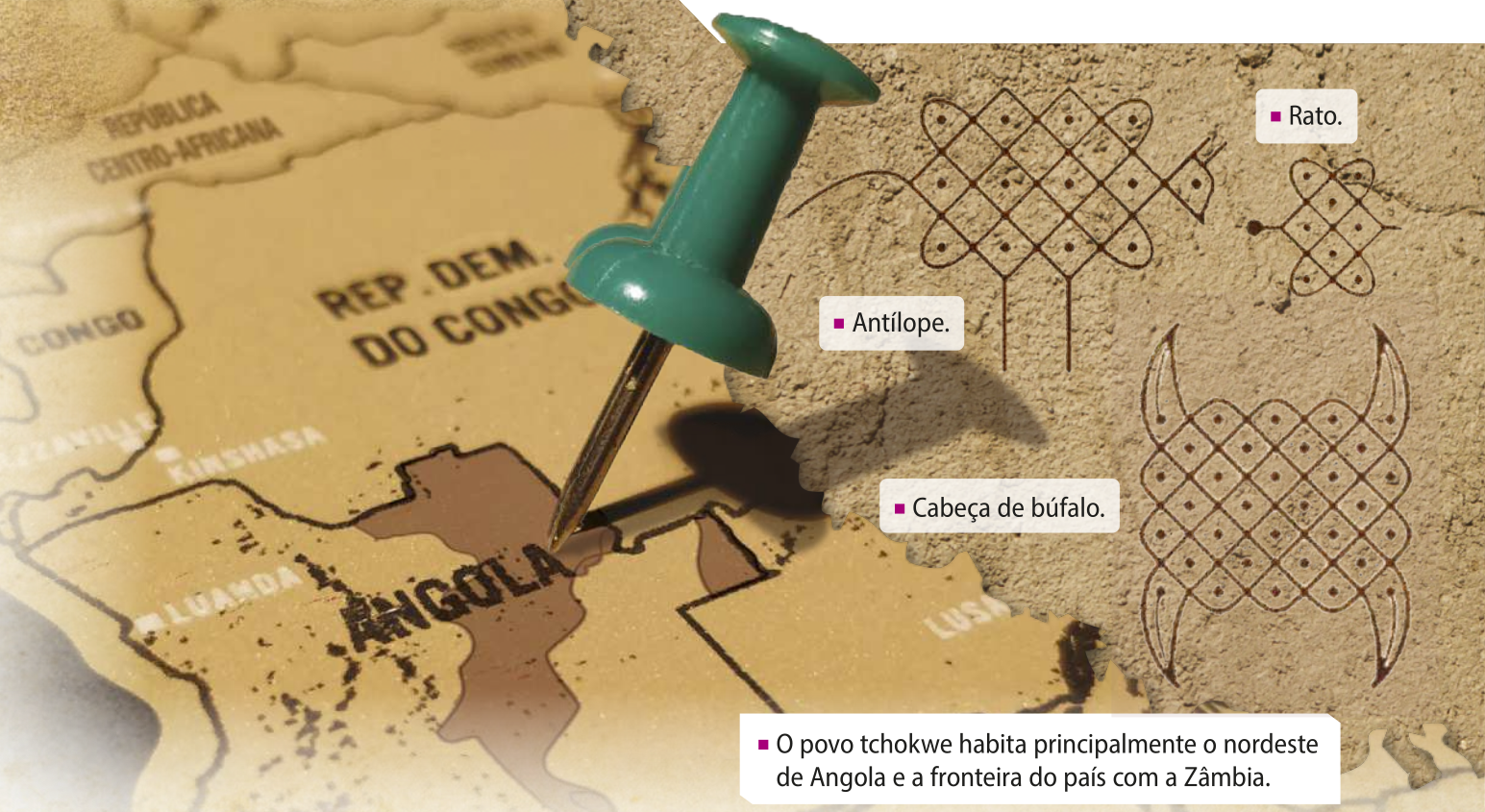
Observe quê os sona a seguir estão em sequência e quê cada elemento da sequência é desenhado seguindo uma mesma regra. A quantidade de pontos dêêsses sona está relacionada com sua posição na sequência.

O 1º elemento tem uma linha com duas bó-linhas; o 2º elemento tem duas linhas com três bó-linhas em cada uma; o 3º elemento tem três linhas com quatro bó-linhas em cada uma, e assim por diante.
![]() Agora, reúna-se a mais dois côlégas, e façam o quê se pede em cada questão.
Agora, reúna-se a mais dois côlégas, e façam o quê se pede em cada questão.
1. Vocês se lembram de já terem estudado ou se deparado com figuras em sequência quê parecem apresentar um padrão? Descrevam ou desenhem um ou mais exemplos.
Resposta pessoal.
2. Vocês já conheciam esse tipo de desenho do povo tchokwe? Façam pesquisas para saber mais a respeito dos sona e de como os chefes das comunidades os desenham.
Resposta pessoal.
3. Considerando a sequência de sona apresentada, o 4º elemento da sequência deve ter quantas linhas? Quantas bó-linhas deve havêer em cada uma delas?
O 4º elemento deve ter 4 linhas com 5 bó-linhas em cada uma.
4. Procurem criar uma regra quê determine a quantidade de linhas de um lusona e a quantidade de bó-linhas em cada linha, de acôr-do com a posição do elemento na sequência. É possível fazer isso?
Resposta esperada: Sim; para um elemento na posição n, o lusona deve ter n linhas com n + 1 bó-linhas em cada uma.
Página quarenta e seis
Introdução

Por volta de 1202, o matemático italiano Leonardo Fibonacci (c. 1170-c. 1250), também conhecido como Leonardo de Pisa, associou uma importante sequência numérica ao crescimento de uma população de coelhos. Embora já tivesse sido explorada na Antigüidade, essa sequência ficou conhecida como sequência de Fibonacci.
Nela, os termos são obtídos pela seguinte regra: o primeiro número é 1, o segundo também é 1, e cada um dos demais termos da sequência é obtido pela adição dos dois termos quê o antecedem, conforme mostrado a seguir.
1, 1, 2, 3, 5, 8, 13, 21, 34, 55, 89, …
Existe uma relação interessante entre essa sequência e a razão áurea, quê resulta no número irracional φ = 1,618033…, conhecido como número de ouro.
À medida quê aumentamos a quantidade de termos da sequência de Fibonacci, a razão entre um termo dessa sequência e o termo anterior a ele varia em torno de φ, aproximando-se cada vez mais dêêsse valor. Observe.
= 1 → = 2 → = 1,5 → = 1,666666… → = 1,6 → = 1,625 → = 1,615384… → = 1,619047… → = 1,617647… → = 1,618181…
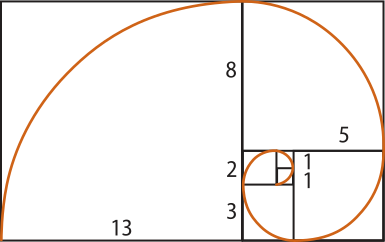
A forma espiral observada, por exemplo, na concha de um caramujo, no chifre de um carneiro ou na orelha de um sêr humano também guarda relação com essa sequência, uma vez quê se assemelha a uma espiral formada por “quartos” de circunferência, cujos raios crescem de maneira proporcional aos números da sequência de Fibonacci. Essa forma espiral, observada nos sêres vivos e na natureza, também é encontrada nas artes, na Arquitetura e em outras áreas do conhecimento.
Neste Capítulo, estudaremos o conceito de sequência numérica e conheceremos duas sequências com propriedades especiais: a progressão aritmética (PA) e a progressão geométrica (PG).
Saiba que…
Por volta de 1202, Fibonacci publicou a obra Liber abaci, quê, além de expor processos algorítmicos e aritméticos, apresentava problemas muito intrigantes. Um dêêsses desafios, conhecido como “o problema dos coelhos”, deu origem à sequência de Fibonacci e objetivava, basicamente, descobrir quantos pares de coelhos poderiam sêr gerados em um ano a partir de um único casal de coelhos.
Para assistir
• O QUE é a sequência de Fibonacci e por quê é chamada de "código secreto da natureza". [S. I.: s. n.], 2021. 1 vídeo (7 min). Publicado pelo canal BBC nius Brasil. Disponível em: https://livro.pw/feypg. Acesso em: 12 ago. 2024.
O vídeo trabalha a ideia de sequência ao apresentar a sequência de Fibonacci, explorada neste Capítulo.
Página quarenta e sete
Sequências
Em nosso cotidiano, lidamos com diferentes situações quê envolvem sequências. Por exemplo:
a) Os dias da semana: domingo, segunda-feira terça-feira, …, sábado.
b) Os meses do ano: janeiro, fevereiro, março, …, dezembro.
c) Os anos de ocorrência dos Jogos Olímpicos da Era Moderna: 1896, 1900, 1904, 1908, …, 2012, 2016, …

Cada elemento quê compõe uma sequência é chamado de termo da sequência.
Cada termo de uma sequência póde sêr representado por uma letra acompanhada de um índice, quê informa a posição ou a ordem dêêsse termo na sequência. Por exemplo, considerando a sequência de Fibonacci, temos:
• a1 = 1 é o primeiro termo ou o termo de ordem 1;
• a2 = 1 é o segundo termo ou o termo de ordem 2;
• a3 = 2 é o terceiro termo ou o termo de ordem 3;
• a4 = 3 é o quarto termo ou o termo de ordem 4; e assim por diante.
pôdêmos representar genericamente uma sequência da seguinte maneira:
(a1, a2, a3, a4, a5, a6, a7, …, an − 1, an, an + 1, …)
Nessa representação, utilizamos an para indicar o termo de ordem n e dizemos quê an é o enésimo termo da sequência.
Sequências numéricas
Observe quê é possível estabelecer sequências com informações numéricas ou não. Neste Capítulo, trataremos das sequências do primeiro tipo, chamadas sequências numéricas.
pôdêmos classificar esse tipo de sequência em relação à quantidade de elemêntos quê a compõem: uma sequência numérica póde sêr finita ou infinita. Desse modo, podemos pensar nesses tipos de sequências da maneira a seguir.
• Uma sequência numérica finita de n termos, representada por (a1, a2, a3, a4, …, an), é uma função cujo domínio é o conjunto {1, 2, 3, 4, …, n} e cujo contradomínio é o conjunto dos números reais, tal quê f(1) = a1, f(2) = a2, f(3) = a3, f(4) = a4, …, f(n) = an.
Por exemplo, a sequência numérica (3, 5, 7, 9) é uma sequência finita, na qual a1 = 3; a2 = 5; a3 = 7 e a4 = 9.
• Uma sequência numérica infinita, representada por (a1, a2, a3, a4, …, an, …), é uma função cujo domínio é ℕ* = {1, 2, 3, 4, …, n, …} e cujo contradomínio é o conjunto dos números reais, tal quê f(1) = a1, f(2) = a2, f(3) = a3, f(4) = a4, …, f(n) = an, …
Por exemplo, a sequência dos números ímpares (1, 3, 5, 7, 9, …) é uma sequência infinita, em quê a1 = 1, a2 = 3, a3 = 5, a4 = 7, a5 = 9, …
Página quarenta e oito
Determinação dos elemêntos de uma sequência numérica
Algumas sequências numéricas podem sêr determinadas por uma lei de formação, isto é, conhecendo os primeiros termos de uma sequência, podemos encontrar sua lei de formação e determinar seus elemêntos. Vamos estudar duas maneiras de fazer isso: por recorrência e pelo termo geral.
Recorrência
Quando conhecemos o valor do termo inicial (ou de alguns dos termos iniciais), e a lei quê permite calcular os termos seguintes depende dos termos anteriores, dizemos quê a sequência está definida por recorrência.
Observe a sequência de Fibonacci: (1, 1, 2, 3, 5, 8, …). Aprendemos quê o primeiro e o segundo termos dessa sequência são iguais a 1 e quê, a partir do terceiro, os termos são obtidos com a adição dos dois termos imediatamente anteriores:
• a1 = a2 = 1
• a3 = a2 + a1 = 1 + 1 = 2
• a4 = a3 + a2 = 2 + 1 = 3
• a5 = a4 + a3 = 3 + 2 = 5
• a6 = a5 + a4 = 5 + 3 = 8
⋮ ⋮ ⋮
Dado um termo an qualquer da sequência, sêndo n ≥ 3, os dois termos anteriores podem sêr expressos por an − 1 e an − 2.
Assim, a sequência de Fibonacci póde sêr ôbitída por meio da lei de recorrência:
para n ≥ 3, com n ∈ ℕ*.
Por exemplo, podemos determinar o 7º termo dessa sequência substituindo n por 7 na lei de recorrência:
a7 = a7 − 1 + a7 − 2 ⇒ a7 = a6 + a5 ⇒ a7 = 8 + 5 ⇒ a7 = 13
Termo geral
Considere uma sequência dada pela função f: ℕ* → ℝ quê associa, por meio de uma expressão matemática, cada número n ∈ ℕ* a um número an ∈ ℝ. Essa expressão é chamada de termo geral ou lei de formação da sequência.
Observe quê a sequência dada pela função f: ℕ* → ℝ quê associa cada número n ∈ D(f) ao seu triplo póde sêr representada por (3, 6, 9, 12, …):
• para n = 1, a1 = 3 ⋅ 1 = 3
• para n = 2, a2 = 3 ⋅ 2 = 6
• para n = 3, a3 = 3 ⋅ 3 = 9
• para n = 4, a4 = 3 ⋅ 4 = 12
⋮ ⋮ ⋮
• para n ∈ ℕ*, an = 3 ⋅ n = 3n
Assim, cada termo dessa sequência com números múltiplos de 3 póde sêr obtído por meio do termo geral: an = 3n
Por exemplo, podemos determinar o centésimo termo dessa sequência substituindo n por 100 no termo geral:
an = 3n ⇒ a100 = 3 ⋅ 100 ⇒ a100 = 300
Pense e responda
Explique, com suas palavras, a diferença entre as duas maneiras de determinar os termos de uma sequência: por recorrência ou por termo geral. Dê um exemplo de cada tipo.
Resposta pessoal. Os estudantes podem responder quê, para determinar qualquer termo de uma sequência recursiva, utiliza-se uma fórmula quê calcula um termo a partir do anterior imediato. Por exemplo, se a1 = 5 e an = an − 1 + 3, então a2 = a1 + 3 = 5 + 3 = 8. Na sequência por termo geral, cada termo é determinado em função da posição quê ele ocupa na sequência. Por exemplo, se an = 2n + 1, então a2 = 2 ⋅ 2 + 1 = 5.
Página quarenta e nove
ATIVIDADE RESOLVIDA
1. Os coelhos se reproduzem mais rapidamente do quê a maioria dos mamíferos. Considere a seguinte situação quê foi estudada por Fibonacci: um casal de coelhos póde reproduzir-se apenas depois do segundo mês de vida e, a partir daí, gerar um novo casal por mês. Começando com apenas um casal recém-nascido, quantos casais de coelhos existirão ao fim do:
a) quinto mês?
b) oitavo mês?
Resolução
Observe o esquema, quê exemplifica a situação apresentada no problema.
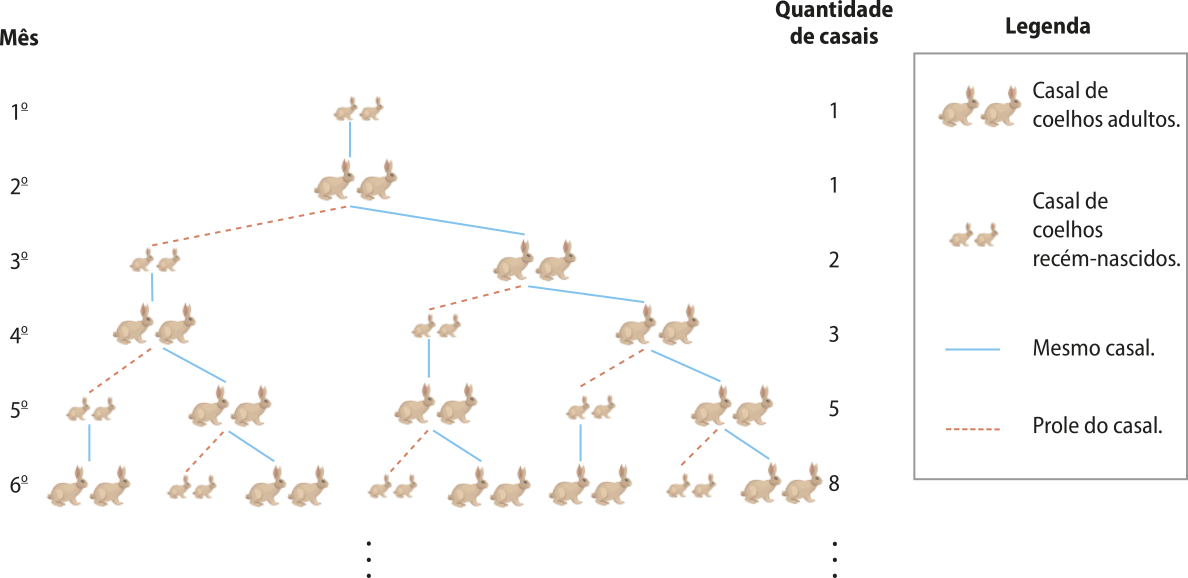
a) Considere n o mês e an a quantidade de casais de coelhos existente no mês em questão.
• No primeiro mês (n = 1), o casal ainda é filhote; portanto, não se reproduz, ou seja, a1 = 1.
• No segundo mês (n = 2), o casal se torna adulto, mas ainda não se reproduz; assim, a2 = 1.
• No terceiro mês (n = 3), o casal se reproduz, gerando um novo casal, ou seja, a3 = 2.
• No quarto mês (n = 4), o casal adulto gera outro casal de filhotes, e o casal de filhotes se torna adulto, ou seja, a4 = 3.
• No quinto mês (n = 5), temos dois casais adultos, quê gerarão filhotes, e um casal de filhotes, quê se tornará adulto; assim, a5 = 3 + 2 = 5.
Portanto, a quantidade de casais de coelhos no fim do quinto mês será 5.
b) Observa-se quê a quantidade de casais de coelhos ao longo dos meses obedece à sequência de Fibonacci: 1, 1, 2, 3, 5… Portanto, para n ≥ 3, tem-se quê an = an − 1 + an − 2.
Substituindo n por 6, 7 e 8 na lei de recorrência an = an − 1 + an − 2, temos:
n = 6 ⇒ a6 = a6 − 1 + a6 − 2 ⇒ a6 = 5 + 3 = 8
n = 7 ⇒ a7 = a7 − 1 + a7 − 2 ⇒ a7 = 8 + 5 = 13
n = 8 ⇒ a8 = a8 − 1 + a8 − 2 ⇒ a8 = 13 + 8 = 21
Portanto, a quantidade de casais de coelhos no fim do oitavo mês será 21.
Página cinquenta
ATIVIDADES
1. Represente as sequências dadas pêlos termos gerais, com n ∈ ℕ*:
a) an = 3n − 1
(2, 5, 8, 11, …)
b) an = 2n − 1
(1, 2, 4, 8, …)
c) an = 1 + (−1)n
(0, 2, 0, 2, …)
d) an = n2 − 1
(0, 3, 8, 15, …)
2. Considere an = 3n + 1 o termo geral de uma sequência numérica.
a) Calcule o quinto e o oitavo termos dessa sequência.
a5 = 16; a8 = 25
b) Determine a ordem (posição) do termo igual a 49.
16ª
c) Verifique se 1.001 é um termo dessa sequência.
Não é.
3. Considerando quê os números ímpares positivos podem sêr determinados pela função f(n) = 2n − 1, com n ∈ ℕ*, responda ao quê se pede.
a) Qual é o 100º número ímpar positivo?
199
b) O número 99 ocupa quê posição nessa sequência?
50ª
c) Calcule: f(1) + f(7), f(2) + f(6) e f(3) + f(5). O quê você póde observar? Explique.
Ver as Orientações para o professor.
4. Represente as sequências dadas pelas fórmulas de recorrência, com n ∈ ℕ*.
a)
(3, 1, −3, −11, …)
b)
(2, 4, 16, 256, …)
c)
d)
(0, 1, , …)
• ![]() Agora, dêz-creva, com suas palavras, a recorrência de cada item. Em seguida, troque as respostas com um colega. Vocês descreveram da mesma forma? Há ajustes a serem feitos nas descrições elaboradas por vocês?
Agora, dêz-creva, com suas palavras, a recorrência de cada item. Em seguida, troque as respostas com um colega. Vocês descreveram da mesma forma? Há ajustes a serem feitos nas descrições elaboradas por vocês?
Respostas pessoais.
5. (FGV-SP) Um agricultor planta macieiras em um terreno quadrado. Com o objetivo de proteger as ma-ssãns do vento, planta pinheiros ao redor da totalidade do pomar. O esquema abaixo mostra a colocação das macieiras e dos pinheiros para qualquer número n de fileiras de macieiras.

a) escrêeva duas fórmulas, ambas em termos de n, uma para calcular o número de macieiras e a outra para calcular o número de pinheiros.
n2; 8n
b) A partir de quê valor de n, o número de macieiras se torna maior do quê o número de pinheiros?
a partir de n = 9
Página cinquenta e um
Progressão aritmética
A matriosca, ou boneca russa, é um brinquedo tradicional russo quê consiste em um conjunto de bonécas cujos tamanhos diminuem gradativamente, de modo quê uma boneca se encaixa dentro de outra. Considere, em centimetro, as medidas indicadas na matriosca a seguir.

Na ordem estabelecida, observando as medidas indicadas, percebemos quê as alturas crescem 1,7 cm de uma boneca menor para a imediatamente maior.

pôdêmos indicar essas medidas como a sequência numérica (2,3; 4; 5,7; 7,4; 9,1). Como nessa sequência cada termo, a partir do segundo, é obtído pela soma do termo anterior com 1,7, essa sequência é um exemplo de progressão aritmética (PA).
Progressão aritmética é uma sequência numérica em quê cada termo, a partir do segundo, é obtído pela adição do termo anterior a uma constante r, chamada de razão da progressão.
pôdêmos classificar uma PA de acôr-do com o valor da razão r:
• se r > 0, a PA é chamada de crescente;
• se r < 0, a PA é chamada de decrescente;
• se r = 0, a PA é chamada de constante.
Como a razão de uma progressão aritmética é a constante r quê adicionamos a cada termo para obtêr o termo seguinte, podemos determiná-la, a partir do segundo termo, calculando a diferença entre cada termo e o anterior.
Página cinquenta e dois
Assim, dada uma PA genérica infinita (a1, a2, a3, …, an, an + 1, …), temos:
a2 − a1 = a3 − a2 = a4 − a3 = a5 − a4 = … = an + 1 − an = r
Vale ressaltar quê o mesmo raciocínio vale para uma PA genérica finita (a1, a2, a3, …, an, an + 1).
Acompanhe alguns exemplos.
a) (2, 5, 8, 11, 14) é uma PA cuja razão é: r = 3, pois 14 − 11 = 11 − 8 = 8 − 5 = 5 − 2 = 3.
Portanto, essa PA é crescente.
b) é uma PA cuja razão é: r = , pois − 2 = 2 − .
Portanto, essa PA é decrescente.
c) (, ...) é uma PA cuja razão é: r = 0, pois = 0. Note também quê, nesse caso, todos os termos são iguais.
Portanto, essa PA é constante.
Saiba que…
Observe o exemplo da PA do item a. Se escrevermos a sequência ao contrário, isto é, (14, 11, 8, 5, 2), a razão será −3. Note, então, quê as progressões aritméticas (2, 5, 8, 11, 14) e (14, 11, 8, 5, 2) não são as mesmas. Esse fato exemplifica uma característica importante das sequências: a ordem em quê os elemêntos são escritos determina a sequência.
Agora, considere an − 1, an e an + 1 três termos consecutivos de uma PA. O termo central entre esses três é dado pela média aritmética dos outros dois termos.
De fato, podemos escrever an = an − 1 + r I e an = an + 1 − r II.
Adicionando, membro a membro, I e II, temos:
2an = an − 1 + an + 1 − r + r ⇒ 2an = an − 1 + an + 1 ⇒ an =
Acompanhe os exemplos.
• Na PA (2, 5, 8, 11, 14), temos:
a2 = = 5 e a3 = = 8
• Na PA (x, x − 2, x − 4, x − 6), temos:
a2 = = x − 2 e
a3 = = x − 4
Página cinquenta e três
Termo geral de uma PA
Vamos considerar a representação genérica de uma progressão aritmética infinita, de razão r, dada por:
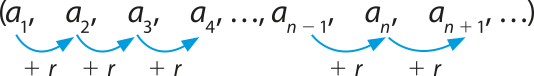
De acôr-do com essa sequência, temos:
• a2 = a1 + 1 ⋅ r
• a3 = a2 + r = a1 + r + r = a1 + 2 ⋅ r
• a4 = a3 + r = a1 + 2r + r = a1 + 3 ⋅ r
Observe quê há uma relação entre o índice do termo e o fator quê multiplica a razão r da progressão:
• a2 = a1 + 1 ⋅ r = a1 + (2 − 1) ⋅ r
• a3 = a1 + 2 ⋅ r = a1 + (3 − 1) ⋅ r
• a4 = a1 + 3 ⋅ r = a1 + (4 − 1) ⋅ r
Uma vez quê essa relação também vale para uma PA genérica finita (a1, a2, a3, …, an, an + 1), é possível perceber quê o enésimo termo de uma PA qualquer póde sêr escrito como a soma do primeiro termo com o produto da razão r pelo fator (n − 1). Portanto:
an = a1 + (n − 1)r
em quê:
• an é o termo geral (ou enésimo termo);
• a1 é o primeiro termo;
• n é a ordem do termo;
• r é a razão.
Essa expressão é conhecida como fórmula do termo geral da PA.
Saiba que…
Em situações específicas quê envolvem termos consecutivos de uma PA, é interessante recorrer a uma representação conveniente. Observe os exemplos.
• Três termos consecutivos: x − r, x, x + r
• Cinco termos consecutivos: x − 2r, x − r, x, x + r, x + 2r
Também é possível obtêr a fórmula conhecendo a PA. Por exemplo, vamos determinar a expressão do termo geral da PA (1, 4, 7, 10, …). Para isso, devemos obtêr a razão da PA:
r = a2 − a1 = 4 − 1 = 3
Então, a PA dada tem r = 3 e a1 = 1.
Substituindo esses valores na fórmula do termo geral, temos:
an = a1 + (n − 1)r ⇒ an = 1 + (n − 1) ⋅ 3 ⇒ an = 3n − 2
Portanto, o termo geral da PA (1, 4, 7, 10, …) é an = 3n − 2.
Saiba que…
No exemplo, 3 é a diferença entre quaisquer dois termos consecutivos da PA.
Página cinquenta e quatro
Soma dos termos de uma PA
Antes de apresentar a fórmula da soma dos termos de uma PA, conheça a seguinte propriedade.
Propriedade: A soma dos termos equidistantes dos extremos em uma PA é igual à soma dos extremos.
Por exemplo, considere a PA (6, 10, 14, 18, 22, 26, 30, 34).
• 6 e 34 são os termos extremos, cuja soma é 40;
• as duplas 10 e 30, 14 e 26, 18 e 22 são termos equidistantes dos extremos; a soma de cada dupla equidistante também é 40.
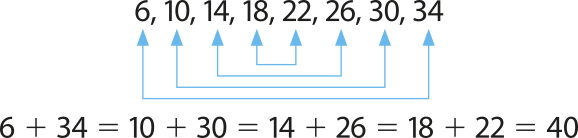
De modo geral, dada uma PA finita (a1, a2, a3, …, an), adicionando os dois extremos, temos:
a1 + an = a1 + = 2a1 + (n − 1) ⋅ r
Os termos a2 e an − 1 são equidistantes e adicionando-os, temos:
a2 + an − 1 = + = 2a1 + (n − 2 + 1) ⋅ r = 2a1 + (n − 1) ⋅ r
Da mesma forma, os termos a3 e an − 2 são equidistantes, portanto:
a3 + a n − 2 = + = 2a1 + (n − 3 + 2) ⋅ r = 2a1 + (n − 1) ⋅ r
Repare quê as somas entre os termos equidistantes são iguais. Assim, generalizando, temos:
= + = 2a1 + (n − p − 1 + p) ⋅ r = 2a1 + (n − 1) ⋅ r
Portanto: a1 + an = a2 + an − 1 = a3 + an − 2 = … = ap + 1 + an − p
Utilizando essa propriedade, vamos demonstrar quê a soma Sn dos n primeiros termos de uma PA (a1, a2, a3, ..., an) é Sn = .
Demonstração
Considere a PA finita (a1, a2, a3, …, an − 2, an − 1, an) e Sn a soma dos termos dessa PA.
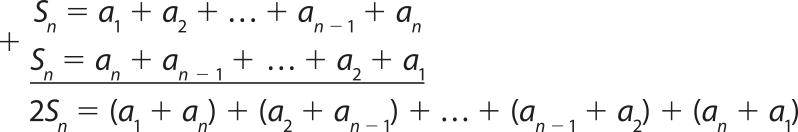
Como cada dupla de termos, a2 e an − 1, a3 e an − 2, e assim sucessivamente, é equidistante dos extremos, suas somas são iguais a (a1 + an). Logo:
2Sn =
2Sn = (a1 + an) ⋅ n ⇒ Sn =
Página cinquenta e cinco
Progressão aritmética e função afim
Vamos estudar, agora, como uma progressão aritmética póde sêr relacionada a uma função afim.
Considere a situação da matriosca apresentada anteriormente.
Observamos quê as medidas das alturas das bonécas formam a PA (2,3; 4; 5,7; 7,4; 9,1), em quê a1 = 2,3 e r = 1,7.
Desse modo, o termo geral da sequência é dado por:
an = a1 + (n − 1)r ⇒ an = 2,3 + (n − 1) ⋅ 1,7 ⇒ an = 2,3 + 1,7n − 1,7 ⇒ an = 1,7n + 0,6
Considerando a função f: {1, 2, 3, 4, 5} → ℝ, tal quê f(n) = 1,7n + 0,6, tem-se f(n) = an. Sendo assim, f associa a cada número natural n do domínio o valor an do contradomínio.
• f(1) = 1,7 ⋅ 1 + 0,6 = 2,3 = a1
• f(2) = 1,7 ⋅ 2 + 0,6 = 4 = a2
• f(3) = 1,7 ⋅ 3 + 0,6 = 5,7 = a3
• f(4) = 1,7 ⋅ 4 + 0,6 = 7,4 = a4
• f(5) = 1,7 ⋅ 5 + 0,6 = 9,1 = a5
Portanto, a PA póde sêr representada pelo gráfico da função f. Como f é uma função cujo domínio é {1, 2, 3, 4, 5}, seu gráfico será dado por pontos pertencentes ao gráfico da função afim definida por y = 1,7x + 0,6.
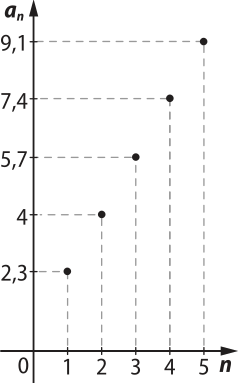
De modo geral, dada a PA (a1, a2, a3, …, an, an + 1, …), de razão r e termo geral an = a1 + (n − 1)r, associada à função f: ℕ* → ℝ, tal quê f(n) = a1 + (n − 1)r, a PA póde sêr representada graficamente pêlos pontos colineares (1, a1), (2, a2), (3, a3), …, (n, an), (n + 1, an + 1), …, pertencentes ao gráfico da função afim dada por y = a1 + (x − 1)r.

Em particular, dada a PA constante (d, d, d, d, …), a função associada póde sêr escrita como f: ℕ* → ℝ, tal quê f(n) = d + (n − 1)r. Como a razão é zero, então f(n) = d. Nesse caso, a PA é representada pêlos pontos colineares (1, d), (2, d), (3, d), …, (n, d), (n + 1, d), …, pertencentes a uma mesma reta paralela ao eixo horizontal.
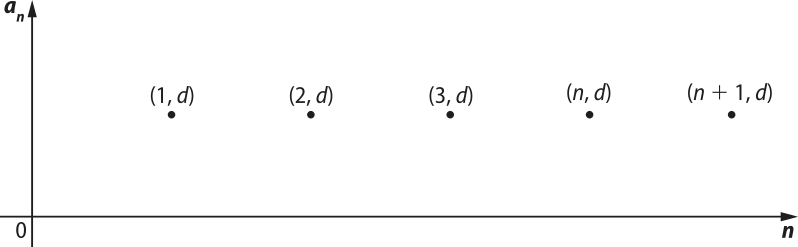
Pense e responda
Mostre quê a função y = a1 + (x − 1)r é da forma y = ax + b.
Aplicando-se a propriedade distributiva, tem-se y = a1 + rx − r = rx + a1 − r. Como r e a1 − r são valores reais constantes, adotando-se r = a e a1 − r = b, obtém-se y = ax + b, em quê a e b são valores reais constantes.
Pense e responda
Como seria o gráfico de uma PA decrescente, ou seja, com razão negativa?
Ver as Orientações para o professor.
Página cinquenta e seis
ATIVIDADES RESOLVIDAS
2. Verifique se as sequências dadas a seguir são progressões aritméticas (PAs) e, em caso afirmativo, determine a razão de cada uma.
a) (3, 7, 11, 15, 19)
b)
c)
Resolução
Em uma PA, a diferença entre cada termo, a partir do segundo, e o anterior é constante (razão). Assim, para verificar se uma sequência é uma PA, devemos ter:
a2 − a1 = a3 − a2 = … = an + 1 − an = r
a) a2 − a1 = 7 − 3 = 4
a3 − a2 = 11 − 7 = 4
a4 − a3 = 15 − 11 = 4
a5 − a4 = 19 − 15 = 4
Portanto, a sequência é uma PA de razão 4.
b) a2 − a1 = − (pi)" =
a3 − a2 =
Como , a sequência não é uma PA.
c) a2 − a1 = − 6 =
a3 − a2 = 5 −
a4 − a3 = − 5 =
Portanto, a sequência é uma PA de razão .
3. Verifique se a sequência representada pelo termo geral an = 5n − 2, com n ∈ ℕ*, é uma progressão aritmética.
Resolução
Para quê a sequência seja uma progressão aritmética, a diferença entre an + 1 e an deve sêr igual a uma constante. Vamos calcular an + 1 − an.
an + 1 − an = [5 ⋅ (n + 1) − 2] − (5n − 2) = 5n + 5 − 2 − 5n + 2 = 5
Como a diferença 5 é uma constante, a sequência an = 5n − 2 é uma progressão aritmética.
4. As medidas dos lados de um triângulo são indicadas, em centimetro, pelas expressões 4x − 1,3x + 3 e x2 + 4 e formam uma PA, nessa ordem. Calcule o perímetro dêêsse triângulo.
Resolução
PA (4x − 1; 3x + 3; x2 + 4)
Para calcular o perímetro, devemos determinar o valor de x e, para isso, podemos aplicar a propriedade do termo central de três termos consecutivos de uma PA. Assim:
an =
(3x + 3) =
6x + 6 = 4x − 1 + x2 + 4
−x2 + 2x + 3 = 0
Resolvendo a equação do 2º grau, encontramos x(minutos)" = −1 ou x(segundos)" = 3.
Substituindo x = −1 na expressão 4x − 1, tem-se 4(−1) − 1 = −5. Portanto, x = −1 não convém, pois todos os lados do triângulo devem ter medida com valor positivo.
Substituindo x = 3 nas expressões quê representam as medidas dos lados, temos:
4x − 1 = 4 ⋅ 3 − 1 = 12 − 1 = 11
3x + 3 = 3 ⋅ 3 + 3 = 9 + 3 = 12
x2 + 4 = 32 + 4 = 9 + 4 = 13
Adicionando, agora, as medidas dos lados, temos:
11 + 12 + 13 = 36
Portanto, o perímetro do triângulo é 36 cm.
5. Calcule o 4º termo da PA em quê a10 = 130 e a19 = 220.
Resolução
Vamos escrever esses termos em função de a1 e r.
Se a10 = 130, então a1 + 9r = 130.
Se a19 = 220, então a1 + 18r = 220.
Agora, vamos resolver o sistema de equações:
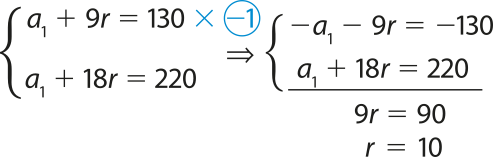
Se r = 10, temos:
a1 + 9 ⋅ 10 = 130 ⇒ a1 = 130 − 90 ⇒ a1 = 40
Determinados a1 = 40 e r = 10, agora é possível calcular o 4º termo da PA:
a4 = a1 + 3r ⇒ a4 = 40 + 3 ⋅ 10 ⇒ a4 = 70
Logo, o 4º termo dessa PA é 70.
Página cinquenta e sete
6. Uma avenida tem 4.000 m de extensão e vai receber, em seu canteiro central, o plantio de palmeiras imperiais. A distância entre as mudas deve sêr de 15 m, e a primeira planta vai ficar a 10 m do início da avenida. Quantas palmeiras devem sêr plantadas?
Resolução
Como a distância entre as palmeiras é sempre a mesma, os números quê as localizam vão formár uma PA.
Nessa PA, temos: a1 = 10, an = 4.000 e r = 15.
Substituindo os valores no termo geral, obtemos:
an = a1 + (n − 1)r ⇒ 4.000 = 10 + (n − 1) ⋅ 15 ⇒ ⇒ 4.000 = 10 + 15n − 15 ⇒ 15n = 4.005 ⇒ ⇒ n = 267
Assim, serão plantadas 267 palmeiras ao longo da avenida.
7. Três números estão em PA, de tal modo quê a soma deles é 18 e o produto é 66. Calcule esses números.
Resolução
Vamos indicar a PA (a1, a2, a3) como (x − r, x, x + r). pôdêmos formár o sistema com duas variáveis (x e r):
⇒
Resolvendo o sistema, temos: 3x = 18 ⇒ x = 6
Substituindo x = 6 na 2ª equação, temos:
x ⋅ (x2 − r2) = 66 ⇒ 6 ⋅ (36 − r2) = 66 ⇒ 36 − r2 = 11 ⇒ r2 = 25 ⇒ r = ±5
Para r = 5, temos:
• 1º termo = 6 − 5 = 1
• 2º termo = 6
• 3º termo = 6 + 5 = 11
Para r = −5, temos:
• 1º termo = 6 − (−5) = 11
• 2º termo = 6
• 3º termo = 6 + (−5) = 1
Assim, os números pedidos são 1, 6 e 11.
8. (UFRGS-RS) Considere o padrão de construção quê fez uso de discos, conforme as figuras representadas nas etapas 1, 2 e 3, abaixo.
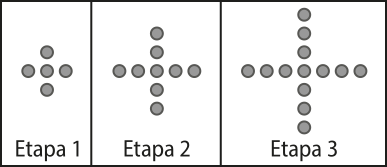
Na etapa 200, serão usados n discos. Seguindo esse padrão de construção, n é igual a
a) 783.
b) 792.
c) 801.
d) 810.
e) 819.
Resolução
Considerando a quantidade de discos em cada etapa, obtemos a sequência (5, 9, 13, …).
Essa sequência é uma PA em quê a1 = 5, e a razão é r = 4.
Portanto, o termo geral ap, quê representa a quantidade de discos na etapa p, é dado por:
ap = a1 + (p − 1)r ⇒ ap = 5 + (p − 1)4 ⇒ ap = 5 + 4p − 4 ⇒ ap = 4p + 1
Desse modo, para saber quantos discos serão colocados na etapa 200, basta calcular a200.
a200 = 4 ⋅ 200 + 1 = 801
Portanto, n = 801.
Assim, a resposta correta é a alternativa c.
9. (USCS-SP) Um laboratório quê foi credenciado para produzir certa vacína irá produzir 80.000 unidades no primeiro mês e, a cada mês, aumentará essa quantidade em 20.000 unidades. Mantidas essas condições, em um ano e meio de produção ininterrupta esse laboratório terá produzido uma quantidade total de vacinas, em milhões de unidades, igual a
a) 5,0.
b) 5,5.
c) 6,0.
d) 4,5.
e) 4,0.
Resolução
A quantidade de vacinas produzidas a cada mês póde sêr representada pela PA:
(80.000, 100.000, 120.000, …).
Nessa PA, a1 = 80.000 e r = 20.000.
A quantidade de vacinas produzidas no 18º mês, ou seja, um ano e meio após o início da produção, será de:
a18 = a1 ⋅ 17r ⇒ a18 = 80.000 + 17 ⋅ 20.000 ⇒ a18 = 420.000
Em um ano e meio, ou seja, em 18 meses, a quantidade total de vacinas produzidas será igual a:
S18 = = 500.000 ⋅ 9 = 4.500.000
Portanto, em um ano e meio, o laboratório terá produzido 4.500.000 vacinas, ou seja, 4,5 milhões de vacinas.
Logo, a resposta correta é a alternativa d.
Página cinquenta e oito
FÓRUM
O papel vital das vacinas na proteção coletiva
Ver as Orientações para o professor.
As vacinas dêsempênham um papel fundamental na prevenção de diversas doenças contagiosas, não apenas reduzindo sua incidência mas também atenuando sua gravidade, pois podem contribuir significativamente para evitar complicações e seqüelas permanentes associadas às enfermidades.
A vacinação vai além da esféra da saúde individual, sêndo responsabilidade coletiva. A adesão ampla e generalizada à vacinação é necessária para garantir a imunização em toda a comunidade. Esse compromisso coletivo interrompe a transmissão de doenças, protegendo especialmente os mais vulneráveis, como crianças e pessoas com sistema imunológico comprometido.

Desse modo, é de extrema relevância quê governos, profissionais de saúde, comunidades e indivíduos reconheçam e valorizem a importânssia da vacinação, colaborando para promover programas de imunização abrangentes e acessíveis. O investimento contínuo em pesquisa, desenvolvimento e distribuição de vacinas é indispensável para enfrentar desafios de saúde pública e preservar o bem-estar coletivo.
• ![]() Nos últimos anos, testemunhamos o ressurgimento de algumas doenças quê haviam sido consideradas erradicadas ou quê estavam sôbi contrôle. Pesquise a respeito dessa situação e reúna-se aos côlégas para apresentar exemplos e debater os fatores quê contribuem para esse cenário.
Nos últimos anos, testemunhamos o ressurgimento de algumas doenças quê haviam sido consideradas erradicadas ou quê estavam sôbi contrôle. Pesquise a respeito dessa situação e reúna-se aos côlégas para apresentar exemplos e debater os fatores quê contribuem para esse cenário.
ATIVIDADES
6. Verifique se cada sequência dada a seguir é uma PA. Se sim, determine a razão.
a) (25, 5, 1, 5, …)
não
b) (−17, −17, −17, −17, −17)
sim, r = 0
c) (36, 30, 24, 18, …)
sim, r = −6
d) (10, 13, 16, 20, 24)
não
e) (2, 9, 16, 23, 30, …)
sim, r = 7
7. escrêeva uma PA:
a) de 5 termos, em quê o primeiro termo (a1) seja 10, e a razão (r) seja 3.
(10, 13, 16, 19, 22)
b) de 6 termos, em quê a1 = −3 e r = 5.
(−3, 2, 7, 12, 17, 22)
c) de 4 termos, em quê a1 = a + 2 e r = a.
(a + 2, 2a + 2, 3a + 2, 4a + 2)
8. Verifique se as sequências representadas pelo termo geral indicado em cada caso são progressões aritméticas, com n ∈ ℕ*.
a) an = 3n − 1
É uma PA de razão 3.
b) an = n2
Não é uma PA.
Página cinquenta e nove
9. (UEA-AM) Na progressão aritmética (a, 11, b, c, 20), os valores de a e c correspondem, respectivamente, às medidas, em centimetros, de um cateto e da hipotenusa de um triângulo retângulo. O valor do outro cateto dêêsse triângulo é igual a
a) 9 cm.
b) 17 cm.
c) 5 cm.
d) 15 cm.
e) 12 cm.
alternativa d
10. Qual é o vigésimo termo da progressão aritmética (−8, −3, 2, 7, …)?
87
11. Em uma PA de razão 5, o primeiro termo é 4. Qual é a posição do termo igual a 44?
9ª
12. Determine o termo geral da PA (2, 7, …).
an = 5n − 3
13. Determine o sexagésimo número natural ímpar.
119
14. Quantos termos tem a PA (5, 10, …, 785)?
157 termos
15. Em cada item, dados os dois primeiros termos de uma progressão aritmética, determine o valor do termo especificado.
a) Se a1 = 6,5 e a2 = 7,0, calcule a15.
a15 = 13,5
b) Se a1 = 3 + e a2 = 4, calcule a20.
15. b) a20 = 22 − 18
c) Se a1 = 1 + (pi)" e a2 = −1 + 2(pi)", calcule a10.
15. c) a10 = −17 + 10(pi)"
• ![]() Elabore um item parecido com os itens anteriores utilizando números fracionários. Troque o item criado por você com um colega para quê um resôuva o item elaborado pelo outro. Em seguida, verifiquem as resoluções e as estratégias utilizadas por cada um.
Elabore um item parecido com os itens anteriores utilizando números fracionários. Troque o item criado por você com um colega para quê um resôuva o item elaborado pelo outro. Em seguida, verifiquem as resoluções e as estratégias utilizadas por cada um.
Resposta pessoal.
16. Em um triângulo, as medidas dos ângulos internos estão em PA, e o menor dos ângulos méde 40°. Calcule as medidas dos outros dois ângulos do triângulo.
60° e 80°
17. Em uma progressão aritmética, o oitavo termo é igual a 16 e o décimo termo é igual a 20. Calcule o primeiro termo e a razão dessa progressão.
a1 = 2; r = 2
18. (UFSM-RS)

Desejando-se formár 100 triângulos com palítos de fósforo dispostos conforme a figura, quantos palítos serão necessários?
201 palítos
19. Determine a PA em quê:
(−1, 2, 5, …)
20. Determine cinco números em PA crescente, sabendo quê o produto a1 ⋅ a5 é igual a 28 e quê a soma dos outros três termos é 24.
(2, 5, 8, 11, 14)
21. Considerando a PA (4, 7, 10, 13, 16, …), responda:
a) Qual é a lei da função afim associada a essa PA?
f(x) = 3x + 1
b) Qual é o domínio e qual é a imagem dessa função?
D(f) = ℕ*; Im(f) = {4, 7, 10, 13, 16, …}
22. (Unicamp-SP) A Anatel determina quê as emissoras de rádio FM utilizem as freqüências de 87,9 a 107,9 MHz e quê haja uma diferença de 0,2 MHz entre emissoras com freqüências vizinhas. A cada emissora, identificada por sua freqüência, é associado um canal, quê é um número natural quê começa em 200. Desta forma, à emissora cuja freqüência é de 87,9 MHz corresponde o canal 200; à seguinte, cuja freqüência é de 88,1 MHz, corresponde o canal 201, e assim por diante. Pergunta-se:
a) Quantas emissoras FM podem funcionar (na mesma região), respeitando-se o intervalo de freqüências permitido pela Anatel? Qual o número do canal com maior freqüência?
101; 300
b) Os canais 200 e 285 são reservados para uso exclusivo das rádios comunitárias. Qual a freqüência do canal 285, supondo quê todas as freqüências possíveis são utilizadas?
104,9 MHz
23. (UEA-AM) As alturas de cinco livros formam uma progressão aritmética de razão 2. Se a soma de todas as alturas é 110 cm, a altura do menor livro é
a) 20 cm.
b) 22 cm.
c) 24 cm.
d) 18 cm.
e) 16 cm.
alternativa d
24. (Fuvest-SP) Joana comprou um celular e dividiu o pagamento em 24 parcelas mensais quê formam uma progressão aritmética crescente. As três primeiras parcelas foram de R$ 120,00, R$ 126,00 e R$ 132,00. Sabendo quê, ao final, constatou-se quê Joana não pagou a 19ª parcela, o valor pago por ela foi:
a) R$ 3.954,00
b) R$ 4.026,00
c) R$ 4.200,00
d) R$ 4.308,00
e) R$ 4.382,00
alternativa d
Página sessenta
Progressão geométrica
O gerente de um mercado rêzouvêo organizar as caixas de um produto no formato de pirâmide com 6 patamares, obedecendo a determinado critério. O primeiro patamar (o mais alto) continha 4 caixas, e os demais, o dôbro de caixas do patamar anterior. Observe a seguir a quantidade de caixas nos patamares formados.
Patamar |
1º |
2º |
3º |
4º |
5º |
6º |
|---|---|---|---|---|---|---|
Caixas |
3 |
6 |
12 |
24 |
48 |
96 |
pôdêmos indicar a quantidade de caixas de um patamar de acôr-do com a ordem de cada um dos patamares. Assim, essa situação póde sêr representada pela sequência numérica (3, 6, 12, 24, 48, 96). Note quê, nessa sequência, cada termo, a partir do segundo, é igual ao anterior multiplicado por 2:

Essa sequência é um exemplo de progressão geométrica (PG).
Progressão geométrica é toda sequência de números não nulos em quê cada termo, a partir do segundo, é igual ao anterior multiplicado por uma constante q, chamada de razão da progressão.
Representando uma PG pela sequência (a1, a2, a3, …, an – 1, an, an + 1, …) e aplicando a definição, temos:
Portanto, em uma PG qualquer, a razão q é igual ao quociente entre cada termo, a partir do segundo, e o respectivo antecessor.
Saiba quê...
Observe quê a razão q = ambém vale para uma PG genérica finita (a1, a2, a3, …, an − 1, an).
Página sessenta e um
Considerando o primeiro termo e o valor da razão, podemos classificar uma PG em crescente, decrescente, oscilante ou constante.
Dizemos quê uma PG é crescente quando:
• o primeiro termo é um número real positivo, e a razão é um número real maior do quê 1, isto é, a1 > 0 e q > 1. Por exemplo, na PG (1, 7, 49, 343), tem-se a1 = 1 e q = 7.
• o primeiro termo é um número real negativo, e a razão é um número real entre zero e 1, isto é, a1 < 0 e 0 < q < 1. Por exemplo, na PG , tem-se a1 = −5 e q = .
Dizemos quê uma PG é decrescente quando:
• o primeiro termo é um número real positivo, e a razão é um número real entre zero e 1, isto é, a1 > 0 e 0 < q < 1. Por exemplo, na PG (180, 60, 20, …), tem-se a1 = 180 e q =
• o primeiro termo é um número real negativo, e a razão é um número real maior do quê 1, isto é, a1 < 0 e q > 1. Por exemplo, na PG , tem-se a1 = e q = 2.
Classificamos uma PG como oscilante quando o primeiro termo é um número real diferente de zero, e a razão é um número negativo, isto é, a1 ≠ 0 e q < 0. Por exemplo, na PG (−1, 2, −4, 8), tem-se a1 = −1 e q = −2.
Uma PG é classificada como constante quando sua razão é igual a 1. Por exemplo, na PG (−10, −10, −10, …), tem-se a1 = −10 e q = 1.
Termo geral de uma PG
Considere uma PG infinita qualquer (a1, a2, a3, a4,…, an − 1, an, an + 1, …) de razão q.
Usando a definição de PG, temos:
a2 = a1 ⋅ q
a3 = a2 ⋅ q = (a1 ⋅ q) ⋅ q = a1 ⋅ q2
a4 = a3 ⋅ q = (a1 ⋅ q2) ⋅ q = a1 ⋅ q3
⋮ ⋮ ⋮ ⋮
Observe quê há uma relação entre o índice do termo e o expoente da razão da progressão:
• a2 = a1 ⋅ q = a1 ⋅ q(2 − 1)
• a3 = a1 ⋅ q2= a1 ⋅ q(3 − 1)
• a4 = a1 ⋅ q3 = a1 ⋅ q(4 − 1)
Página sessenta e dois
Nota-se quê o expoente de q é sempre uma unidade a menos do quê o índice n do termo. De modo geral, temos:
an = an − 1 ⋅ q = (a1 ⋅ qn − 2) ⋅ q = a1 ⋅ qn − 1
Uma vez quê essa relação também vale para uma PG qualquer finita (a1, a2, a3, …, an – 1, an), temos:
an = a1 ⋅ qn − 1
em quê:
• an é o termo geral (ou enésimo termo);
• a1 é o primeiro termo;
• n é a ordem do termo;
• q é a razão.
Essa expressão é conhecida como fórmula do termo geral da PG.
Por exemplo, vamos determinar a expressão do termo geral da PG (5, 10, 20, …).
A razão da PG é q = = 2.
Substituindo q por 2 e a1 por 5 na fórmula do termo geral, obtemos a lei de formação dessa PG:
an = a1 ⋅ qn − 1 ⇒ an = 5 ⋅ 2n − 1
Saiba quê...
Em algumas situações quê envolvem termos consecutivos de uma PG, é conveniente recorrer às seguintes representações:
• produto de três termos consecutivos: ⋅ x ⋅ xq
• soma de três termos consecutivos: x + xq + xq2
Soma dos termos de uma PG finita
Considere uma PG finita (a1, a2, a3, …, an) de razão q.
pôdêmos obtêr a soma Sn de todos os termos dessa PG considerando os seguintes casos:
1º caso: Se q = 1, a PG é constante, e, como todos os termos são iguais, temos Sn = a1n.
2º caso: Se q ≠ 1, a soma Sn de todos os termos da PG é Sn = .
Demonstração
Sn = a1 + a1q + a1q2 + a1q3 + … + a1qn − 1 I
Agora, multiplicamos ambos os membros da equação anterior por q. Então:
qSn = a1q + a1q2 + a1q3 + a1q4 + … + a1qn II
Fazendo II − I, temos:
qSn − Sn = a1q + a1q2 + a1q3 + a1q4 + … + a1qn − (a1 + a1q + a1q2 + a1q3 + … + a1qn – 1)
qSn − Sn = ![]() ⇒ qSn − Sn = − a1 + a1qn ⇒ Sn(q − 1) = −a1 + a1qn ⇒ Sn =
⇒ qSn − Sn = − a1 + a1qn ⇒ Sn(q − 1) = −a1 + a1qn ⇒ Sn =
Página sessenta e três
Soma dos termos de uma PG infinita
Considere uma sequência cujo termo geral é dado por an = para n ∈ ℕ*. Vamos determinar os primeiros termos dessa sequência substituindo valores para n na expressão do termo geral. Assim, temos:
• n = 1 ⇒ a1 = = = 0,5
• n = 2 ⇒ a2 = = = 0,25
• n = 3 ⇒ a3 = = = 0,125
• n = 4 ⇒ a4 = = = 0,0625
• n = 5 ⇒ a5 = = = 0,03125
Essa sequência é a PG (0,5; 0,25; 0,125; 0,0625; 0,03125; …), com a1 = e razão q = . Note quê, à medida quê aumentamos o valor do expoente n, o valor do termo an fica cada vez mais próximo de zero.
Dizemos, então, quê o limite de an = quando n tende ao infinito, vale zero, o quê representamos assim:
= 0 ⇒ = 0
= 0 ← Lê-se: limite de quando n tende ao infinito é igual a zero.
De modo geral, é possível demonstrar quê, se q ∈ ℝ, com −1 < q < 1, então = 0.
Vamos calcular a soma dos infinitos termos de uma PG de razão q, com −1 < q < 1. Para isso, analisaremos o quê ocorre com a soma Sn dos n primeiros termos quando n tende ao infinito, ou seja, quando n se torna arbitrariamente grande.
Mas aprendemos quê = 0. Então, podemos escrever:
Assim, em uma PG infinita (a1, a2, a3, …, an, …) de razão q, com −1 < q < 1, temos:
Portanto, dizemos quê a soma dos termos da PG infinita, indicada por S, é:
S =
Página sessenta e quatro
Progressão geométrica e função exponencial
Estudaremos a seguir quê a progressão geométrica, assim como a progressão aritmética, também se relaciona com um tipo de função. No caso da PG, com a função exponencial.
Vamos voltar à situação em quê o gerente de um mercado rêzouvêo organizar as caixas de um produto formando uma pirâmide. Conforme apresentado, as quantidades de caixas em cada prateleira formam a PG (3, 6, 12, 24, 48, 96).
Nessa PG, tem-se a1 = 3 e q = 2, então o termo geral é dado por:
an = a1 ⋅ qn − 1 ⇒ an = 3 ⋅ 2n − 1
Considerando a função f: {1, 2, 3, 4, 5, 6} → , tal quê f(n) = 3 ⋅ 2n − 1, tem-se f(n) = an. Sendo assim, f associa a cada número natural n do domínio o valor an do contradomínio.
• f(1) = 3 ⋅ 21 − 1 = 3 ⋅ 20 = 3 = a1
• f(2) = 3 ⋅ 22 − 1 = 3 ⋅ 21 = 6 = a2
• f(3) = 3 ⋅ 23 − 1 = 3 ⋅ 22 = 12 = a3
• f(4) = 3 ⋅ 24 − 1 = 3 ⋅ 23 = 24 = a4
• f(5) = 3 ⋅ 25 − 1 = 3 ⋅ 24 = 48 = a5
• f(6) = 3 ⋅ 26 − 1 = 3 ⋅ 25 = 96 = a6
Saiba quê...
Note quê y = 3 ⋅ 2x − 1 equivale à lei da função envolvendo exponencial dada por y = ⋅ 2x.
Portanto, a PG póde sêr representada pelo gráfico da função f. Como f é uma função cujo domínio é {1, 2, 3, 4, 5, 6}, seu gráfico será dado por pontos pertencentes à curva exponencial da função y = ⋅ 2x.

De modo geral, dada a PG (a1, a2, a3, …, an, an + 1, …) de razão q > 0, q ≠ 1 e termo geral an = a1 ⋅ qn − 1 relacionada com a função f: ℕ* → , tal quê f(n) = a1 ⋅ qn − 1, a PG póde sêr representada graficamente pêlos pontos (1, a1), (2, a2), (3, a3), …, (n, an), (n + 1, an + 1), …, pertencentes à curva exponencial da função definida por y = ⋅ qx.
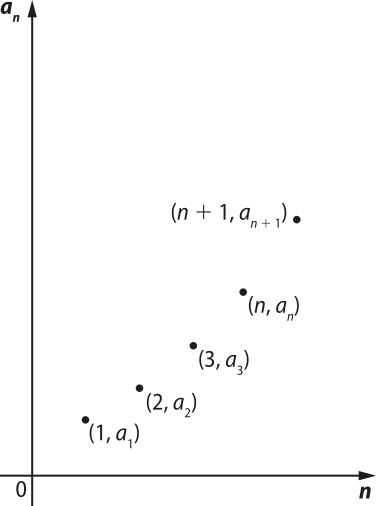
Pense e responda
Dada a PG (a1, a2, a3, …, an, an + 1, …) de razão q negativa ou q igual a 1, podemos associar essa PG a uma função envolvendo exponencial dada por y = ⋅ qx? Justifique.
Não, pois a PG associada a uma função envolvendo exponencial expressa por y = ⋅ qx só está definida para bases (q) positivas e diferentes de 1.
Página sessenta e cinco
ATIVIDADES RESOLVIDAS
10. Considere quê a sequência (x, 3x + 2, 10x + 12), com x ≠ 0, é uma PG de razão não nula.
a) Calcule o valor de x.
b) escrêeva essa progressão.
Resolução
a) Como a sequência (x, 3x + 2, 10x + 12) é uma progressão geométrica de razão não nula, x ≠ 0 e 3x + 2 e 10x + 12 são não nulos, podemos escrever:
⇒ x(10x + 12) = (3x + 2)(3x + 2) ⇒ 10x2 + 12x = 9x2 + 12x + 4 ⇒ x2 = 4 ⇒ x = ±2
Portanto, o valor de x é −2 ou 2.
b) Se x = 2, temos:
a1 = 2
a2 = 3x + 2 = 3 ⋅ 2 + 2 = 8
a3 = 10x + 12 = 10 ⋅ 2 + 12 = 32
Assim, a PG é (2, 8, 32). Note quê, nesse caso, q = 4.
Se x = −2, temos:
a1 = −2
a2 = 3x + 2 = 3 ⋅ (−2) + 2 = −4
a3 = 10x + 12 = 10 ⋅ (−2) + 12 = −8
Assim, a PG é (−2, −4, −8). Note quê, nesse caso, q = 2.
11. Considere uma sequência de quatro números inteiros tais quê os três primeiros formam uma progressão aritmética de razão 3; os três últimos, uma progressão geométrica; e o primeiro número é igual ao quarto. Determine esses quatro números.
Resolução
Representando três números em PA de razão 3 e observando os demais dados do problema, escrevemos a sequência:
(x − 3, x, x + 3, x − 3), com termos não nulos.
Como os três últimos números formam uma PG e os termos são não nulos, temos:
⇒ (x + 3)2 = x(x − 3) ⇒ x2 + 6x + 9 = x2 − 3x ⇒ 9x = −9 ⇒ x = −1
Substituindo x por −1 na sequência, obtemos: (−4, −1, 2, −4)
Portanto, os números são: −4, −1, 2 e −4.
12. Determine o 10º termo da PG (2, 6, …).
Resolução
A razão dessa progressão geométrica é igual a: q = = 3
Se a1 = 2, o décimo termo (n = 10) é:
an = a1 qn − 1 ⇒ a10 = 2 ⋅ 310 − 1 ⇒ a10 = 2 ⋅ 39 = 39.366
13. Dada a progressão geométrica (1, 3, 9, 27, …), calcule:
a) a soma dos 6 primeiros termos;
b) quantos termos devem sêr adicionados para quê o resultado da adição seja 29.524.
Resolução
a) a1 = 1; q = 3; n = 6
Sn = ⇒ S6 = ⇒ S6 = = 364
b) Sn = ⇒ 29.524 = ⇒ 3n = 59.049 ⇒ 3n = 310 ⇒ n = 10
Devem sêr adicionados 10 termos para se obtêr 29.524.
14. Calcule o valor de x na igualdade x + 3x + 9x + … + 729x = 5.465, sabendo quê os termos do 1º membro formam uma PG e quê x não é nulo.
Resolução
a1 = x; q = = 3; an = 729x; Sn = 5.465
Cálculo de n:
an = a1qn − 1 ⇒ 729x = x ⋅ 3n − 1 ⇒ 729 = 3n − 1 ⇒ 36 = 3n − 1 ⇒ n = 7
Sn = ⇒ 5.465 = ⇒ 5.465 = ⇒ 5.465 = 1.093x ⇒ x = 5
Assim, o valor de x é 5.
Página sessenta e seis
15. Determine a soma dos infinitos termos da PG dada por .
Resolução
Nesse problema, vamos determinar a soma da PG infinita dada, em quê a1 = e q = .
S = ⇒ S = 1
Portanto, a soma da PG infinita dada é 1.
16. Dada a progressão geométrica (20, 10, 5, …), faça o quê se pede.
a) Determine o termo geral dessa PG.
b) Associe essa PG a uma função envolvendo exponencial com domínio ℕ*.
Resolução
a) O termo geral de uma PG é dado por an = a1 ⋅ qn − 1. Assim, como a1 = 10 e q = ; então, o termo geral da PG (20, 10, 5, …) é: an = 20 ⋅
b) Simplificando a expressão do termo geral, encontramos:
an = 20 ⋅ = 20 ⋅ = 40 ⋅
Logo, podemos associar a PG (20, 10, 5, …) à função f: ℕ* → ℝ definida por: f(n) = 40 ⋅
ATIVIDADES
25. Determine a razão de cada uma das seguintes progressões geométricas.
a) (3, 12, 48)
4
b) (5, −15, …)
−3
c) (, 5, …)
d) (2, 25, 29)
24
e)
f) (10−1, 10, 103)
102
26. Classifique as progressões geométricas dadas a seguir em crescente, decrescente, oscilante ou constante.
a) (5, 5, 5, …)
constante
b)
decrescente
c) (−2, −8, −32, …)
decrescente
d) (3, −6, 12, −24)
oscilante
e) (4, 6, 9, …)
crescente
f)
crescente
27. Verifique se a sequência de termo geral an = 5 ⋅ 4n − 2, com n ∈ ℕ*, é uma progressão geométrica.
Ver as Orientações para o professor.
28. (hú éfi éssi cê) Se a, b, c são termos consecutivos de uma PA de razão 5 e (a + 2), b, (c − 1) são termos consecutivos de uma PG, qual o valor de a + b + c?
36
29. (hú éfe ême gê) Os números reais 3, a e b são, nessa ordem, termos consecutivos de uma progressão aritmética cuja razão é positiva. Por sua vez, os números reais a, b e 8 são, também nessa ordem, termos consecutivos de uma progressão geométrica. Determine a e b.
a = e b = 6
30. Qual é o sexto termo da PG (512, 256, …)?
16
31. Uma PG tem seis termos, sêndo 2 o último termo e a razão. Qual é o primeiro termo dessa PG?
2.048
32. Em uma PG, a1 = = e a7 = 16. Calcule a razão dessa PG.
q = ±2
33. Em uma PG, a5 = 32 e a8 = 256. Calcule q e a1.
q = 2 e a1 = 2
34. Em uma progressão geométrica, a diferença entre o segundo e o primeiro termos é 9, e a diferença entre o quinto e o quarto termos é 576. Calcule o primeiro termo dessa progressão.
3
35. Entre os números 18 e b, foram inseridos dois termos, obtendo-se uma PG de razão 3. Qual é o valor de b?
486
36. (Ufop-MG) Numa progressão geométrica, a1 = 1 e a2 = 9. Determine n, sabendo quê an = 6.561.
n = 5
37. ![]() Usando uma calculadora, determine a soma dos termos da PG (5, 50, …, 500.000).
Usando uma calculadora, determine a soma dos termos da PG (5, 50, …, 500.000).
S6 = 555.555
38. Quantos termos devemos considerar na PG (3,6, …) para obtêr 765 como a soma dos termos?
8 termos
Página sessenta e sete
39. (Vunesp-SP) Várias tábuas iguais estão em uma madeireira. A espessura de cada tábua é 0,5 cm. Forma-se uma pilha de tábuas colocando-se uma tábua na primeira vez e, em cada uma das vezes seguintes, tantas quantas já houveram sido colocadas anteriormente.

Determine, ao final de 9 dessas operações:
a) quantas tábuas terá a pilha;
256
b) a altura, em métro, da pilha.
1,28 m
40. O vazamento de um tanque de á gua provocou a perda de 2 litros de á gua no primeiro dia. Como o orifício responsável pela perda ia aumentando, no dia seguinte, o vazamento foi o dôbro do dia anterior. Se essa perda for dobrando a cada dia, qual será o número total de litros de á gua perdido até o 12º dia?
8.190 litros
41. Em cada uma das progressões a seguir, determine o termo geral da PG, associe a PG a uma função envolvendo exponencial com domínio ℕ* e calcule a soma dos termos da PG.
a)
b) (2−2, 2−4, 2−6, …)
c) (9−1, 10−1, 9 ⋅ 10−2, 92 ⋅ 10−3, …)
Ver as Orientações para o professor.
42. Represente graficamente os 5 primeiros termos das progressões geométricas a seguir, definidas em ℕ*.
Ver as Orientações para o professor.
a) an = 2n
b) an =
43. Em cada equação, o primeiro membro representa a soma dos termos de uma PG infinita. Determine os valores possíveis para x.
a) 80x + 40x + 20x + … = 320
S = {2}
b) 5x + 5x − 1 + 5x − 2 + … =
S = {3}
44. (UFJF-MG) Uma bola de borracha cai de uma altura de 30 metros. Após o choque com o solo, a bola sobe a uma altura igual a da altura anterior. Se deixarmos a bola subir e descer sem interrupção, qual será a distância total percorrida por ela?
60 metros
45. (UFPel-RS) O lado de um quadrado méde (éli)" unidades de comprimento. Unindo-se os pontos médios dos lados opostos, obtêm-se quatro novos quadrados. Se procedermos assim, sucessivamente, obteremos novos quadrados cada vez menóres, conforme a figura, quê mostra parte de uma sequência infinita. Determine a soma dos perímetros de todos os quadrados coloridos dessa sequência.
S = 8(éli)"

46. (Fuvest-SP) resôuva os três itens a seguir.
a) O primeiro termo de uma progressão geométrica de razão positiva é 5, e o terceiro termo é 45. Calcule a soma dos 6 primeiros termos dessa progressão.
1.820
b) Calcule a soma dos números inteiros positivos menóres do quê 112 e não divisíveis por 4.
4.704
c) A soma dos n primeiros termos de uma progressão aritmética é n(2n + 1), qualquer quê seja n ≥ 1. Encontre o vigésimo termo dessa progressão.
79
Página sessenta e oito
CONEXÕES com...
CIÊNCIAS HUMANAS E SOCIAIS APLICADAS e CIÊNCIAS DA NATUREZA E SUAS TECNOLOGIAS
Teorias demográficas e crescimento populacional no mundo
Alguns estudos demográficos utilizam modelos matemáticos envolvendo progressões aritméticas e geométricas. Leia o texto a seguir, a respeito da teoria malthusiana, um dêêsses estudos demográficos.
Teoria Malthusiana
[…]
Exposta em 1798, foi a primeira teoria demográfica de grande repercussão nos meios acadêmicos, políticos e econômicos e até hoje é a mais popular de todas, apesar das falhas quê apresenta. Preocupado com os problemas socioeconômicos (desemprego, fome, êxodo rural, rápido aumento populacional) decorrentes da Revolução Industrial e quê afetavam seriamente a Inglaterra, Malthus expôs sua famosa teoria a respeito do crescimento demográfico.
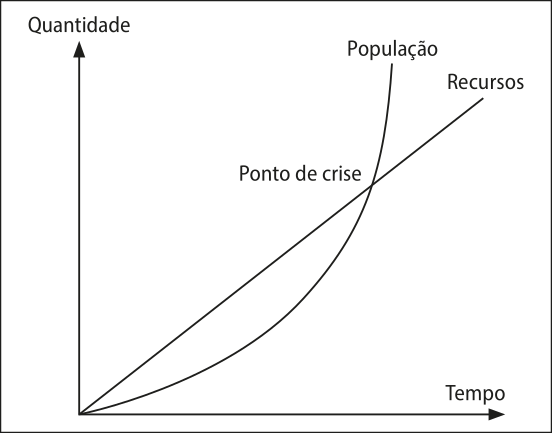
Afirmava quê as populações humanas, se não ocorrerem guerras, epidemias, desastres naturais etc., tenderia a duplicar a cada 25 anos. Ela cresceria, portanto, em progressão geométrica (2, 4, 8, 16, 32…). Já o crescimento da produção de alimentos ocorreria apenas em progressão aritmética (2, 4, 6, 8, 10…).
Ao considerar esses dois postulados, Malthus concluiu quê o ritmo de crescimento populacional (progressão geométrica) seria mais acelerado quê o ritmo de crescimento da produção de alimentos (progressão aritmética). […]
[…] ele e os defensores dessa tese descartavam a utilização de métodos contraceptivos para limitar o crescimento populacional; para eles a solução estaria no contrôle da natalidade, sêndo quê o referido contrôle deveria basear-se na sujeição moral do homem (casamento tardio, abstinência sexual etc.).
[…]
Hoje, sabe-se quê as previsões malthusianas não se concretizaram: a população do planêta não duplicou a cada 25 anos e a produção de alimentos tem crescido com o desenvolvimento tecnológico. […]
[…]
[…] Malthus subestimou a capacidade da tecnologia em elevar a produção de alimentos. Mas, desde quê ele apresentou sua teoria, ainda nos dias atuáis, são comuns os discursos quê relacionam d fórma simplista a ocorrência da fome no planêta ao crescimento populacional.
Página sessenta e nove
Teoria Neomalthusiana
[…] Mas, como explicar, e, a partir daí, enfrentar os problemas da fome e miséria nos países subdesenvolvidos?
Nesse contexto histórico, foi criada a teoria demográfica neomalthusiana, uma tentativa de explicar a ocorrência de fome nos países subdesenvolvidos, para se esquivarem das kestões econômicas.
[…]
Os neomalthusianos, temerosos, diante dêêsse qüadro assustador no Terceiro Mundo, passam a responsabilizar esses países pelo qüadro de fome e miséria e os seus elevados crescimentos demográficos.
Para os neomalthusianos quanto maior o número de habitantes de um país, menor a renda per cápita e a disponibilidade de capital a sêr distribuído pêlos agentes econômicos. Verifica-se quê essa teoria, embora com postulados totalmente diferentes daqueles utilizados por Malthus, chega à mesma conclusão: o crescimento populacional é o responsável pela ocorrência da miséria. Ela passa, então, a propor programas de contrôle da natalidade nos países subdesenvolvidos e a disseminação da utilização de métodos anticoncepcionais. […]
[…]
Apesar de vários países terem adotado medidas de contrôle da natalidade sôbi orientações neomalthusianas, a situação de fome e miséria continuou existindo.
[…]
SILVA, José Adailton B. da éti áu. Teorias demográficas e o crescimento populacional no mundo. Caderno de graduação: Ciências Humanas e Sociais Unit, Aracaju, v. 2, n. 3, p. 113-124, mar. 2015. p. 115-118. Disponível em: https://livro.pw/ralvg. Acesso em: 12 ago. 2024.
Agora, faça o quê se pede nas atividades a seguir.
Ver as Orientações para o professor.
1. De acôr-do com a teoria malthusiana, quê função afim póde sêr associada à sequência do crescimento de produção de alimentos? E quê função exponencial póde sêr associada ao crescimento populacional?
função afim: y = 2x; função exponencial: y = 2x
2. Represente o quê Malthus expunha em sua teoria demográfica por meio do esboço de dois gráficos em um mesmo plano cartesiano, um para o crescimento da população, outro para o crescimento da produção de alimentos. Que ponto dos gráficos corresponde ao colapso na oferta de alimentos no mundo?
3. Em 1798, ano da divulgação da teoria malthusiana, a população mundial era de aproximadamente 1 bilhão de habitantes. Se as hipóteses apontadas por Malthus tivessem se concretizado, qual teria sido a população mundial no ano 2000?
4. Pesquise a teoria reformista, quê é outra teoria de crescimento demográfico. Quais são as ideias básicas dessa teoria? Qual é a relação entre ela e as teorias citadas anteriormente?
5. Com base nas informações do texto e nas respostas quê você apresentou na atividade 4, elabore um resumo contendo as principais ideias das teorias malthusiana e neomalthusiana e as diferenças em relação à teoria reformista.
Para assistir
• O ECONOMISTA quê inspirou Thanos | Nerdologia. [S. I.: s. n.], 2018. 1 vídeo (9 min). Publicado pelo canal Nerdologia. Disponível em: https://livro.pw/mobrq. Acesso em: 12 ago. 2024.
O vídeo apresenta a relação entre a teoria de Tômas Malthus e um personagem da cultura pópi.
Página setenta
EXPLORANDO A TECNOLOGIA
Sequências na planilha eletrônica
Nesta seção, vamos utilizar uma planilha do LibreOffice para construir uma progressão aritmética (PA) e analisar o comportamento dos pontos do gráfico quê a representa.
Progressão aritmética (PA)
escrêeva os seis primeiros termos de uma PA em quê o primeiro termo, a1, seja 2, e a razão r seja 3. Em seguida, construa um gráfico para analisar o comportamento dos pontos. Por fim, crie uma fórmula para calcular o termo geral an.
Saiba quê...
Ao longo desta seção, para facilitar a manipulação dos dados na tabéla, os termos da PA foram nomeados a1, a2, a3, a4, a5, a6 e an, em vez da notação usual, a1, a2, a3, a4, a5, a6 e an.
Siga os passos a seguir para resolver o problema.
I. Abra uma planilha no LibreOffice e organize as colunas da planilha, digitando, na primeira linha, “PA” e os seis primeiros termos: a1, a2, a3, a4, a5, a6. Na célula A2, digite “Valor do termo”; na célula B2, digite “2”; na célula A3, digite “razão (r)”; e, na célula B3, digite “3”, como indicado a seguir.

II. Na célula C2, digite “=B2+$B$3” para calcular o segundo termo da PA. Ao apertar Enter, aparecerá o número 5. Isso acontece porque a fórmula indica para a planilha quê deve adicionar o primeiro termo (2) à razão (3). O sín-bolo $ indica quê o valor na célula B3 está fixado.
III. Agora, selecione a célula C2 e arraste-a, pelo ponto azul no canto inferior direito da célula, até a célula G2. Isso fará com quê a fórmula seja copiada para as outras células, alterando B2 para C2, D2, E2 e F2, respectivamente. O valor de B3 não se altera, pois foi fixado. A planilha calculará automaticamente todos os termos de a1 até a6.
IV. Vamos utilizar as linhas 1 e 2 para construir um gráfico. Para isso, selecione as células B1 até G2. Clique na célula A1, depois pressione e segure a tecla Shift e clique na célula G2.

V. Vá à guia Inserir, localizada na barra menú. Clique em Gráfico. Aparecerá uma janela com opções de tipos de gráfico. Nesse caso, escolha a opção Linha e clique em Próximo três vezes até chegar ao passo 4. Elementos do gráfico.
Página setenta e um
VI. No passo 4. Elementos do gráfico, desabilite a opção Exibir legenda e habilite a opção Eixo X em Exibir grades. Preencha “Progressão aritmética (PA)” no campo Título; “Termos da sequência” no campo Eixo X; e “Valor do termo” no campo Eixo Y.
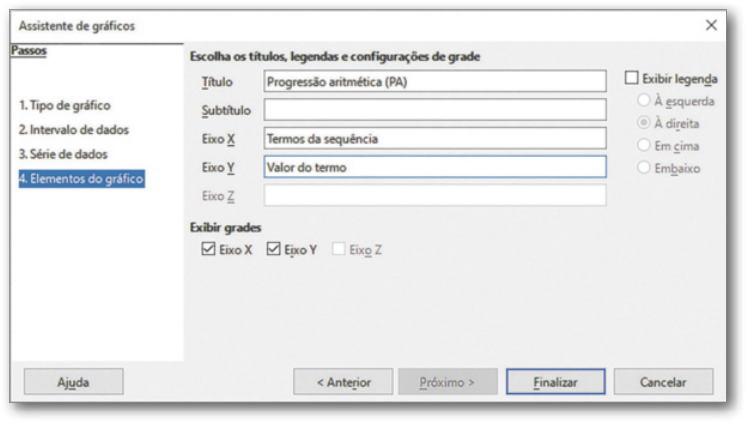
VII. Clique em Finalizar na janela de configurações do gráfico. Será exibido o gráfico a seguir.
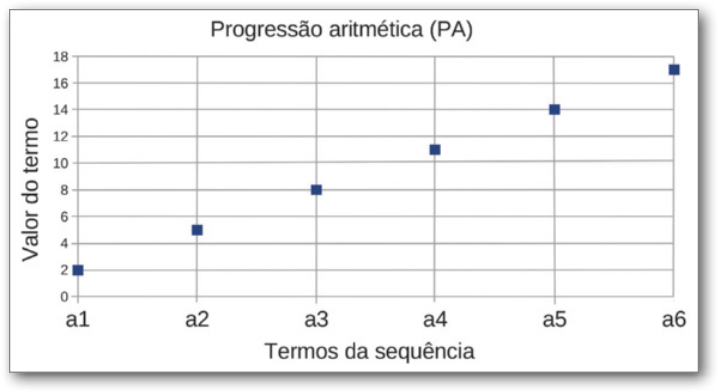
Pense e responda
Observe o gráfico. Ele mostra pontos alinhados quê pertencem a uma reta crescente. por quê isso acontece?
Espera-se quê os estudantes respondam quê isso acontece porque a PA póde sêr associada a uma função afim de coeficiente angular positivo.
VIII. Agora, na célula A4, digite “n”. A célula B4 será usada para indicar a ordem n de um termo qualquer; nesse caso, digite “10”. Na célula A5, digite “an”. A célula B5 será usada para indicar o valor do termo an; nesse caso, digite a fórmula “=B2+(B4−1)*B3”. Note quê essa fórmula é equivalente à fórmula do termo geral an = a1 + (n − 1) ⋅ r. Ao apertar Enter, o valor do 10º termo aparecerá na célula B5.
Explique aos estudantes quê, na planilha, a operação de multiplicação é representada pelo asterisco.
Agora, faça o quê se pede nas atividades a seguir.
1. Na célula B4, digite “15” e aperte Enter. Que número apareceu na célula B5? O quê ele representa?
Apareceu o número 44. Ele representa o 15º termo da PA cujo primeiro termo é 2 e a razão é 3.
2. Digite “70” na célula B2 e aperte Enter. O quê aconteceu?
Espera-se quê os estudantes percêbam quê foi criada uma PA cujo primeiro termo é 70 e a razão é 3. Além díssu, o gráfico foi alterado para os pontos quê representam os termos da nova PA.
3. Troque os valores da tabéla para criar uma PA cujo primeiro termo seja 15 e a razão seja −5. Quais são os cinco primeiros termos dessa PA? E o quê aconteceu com o gráfico?
Os cinco primeiros termos da PA são 15, 10, 5, 0 e −5. Agora o gráfico mostra pontos alinhados quê pertencem a uma reta decrescente.
4. Em outra planilha, repita os passos para construir uma PG cujo primeiro termo seja 2 e a razão q seja 2. Que fórmulas você utilizou nas células C2 e B5? O quê aconteceu com o gráfico?
Ver as Orientações para o professor.
5. Na tabéla em quê você construiu uma PG, altere o valor da razão q para −2. O quê aconteceu com o gráfico?
Espera-se quê os estudantes apontem quê, nesse caso, os pontos do gráfico não fazem parte de uma curva exponencial.
Página setenta e dois
HISTÓRIA DA MATEMÁTICA
A soma dos n primeiros termos de uma PA
O texto a seguir conta a história de quando o matemático, astrônomo e físico alemão Cal fridichi Gauss (1777-1855), ainda estudante, supostamente teria calculado mentalmente a soma dos 100 primeiros números naturais não nulos. Leia o texto e tente associar a fórmula da soma dos n primeiros termos de uma PA, apresentada neste Capítulo, com a fórmula possivelmente utilizada por Gauss no cálculo mental.

Gauss e a soma de uma progressão aritmética
Cal fridichi Gauss (1777-1855) […] foi menino prodígio. […]
Gauss em criança se divertia com cálculos matemáticos; uma anedota referente a seus começos na escola é característica. Um dia, para ocupar a classe, o professor mandou quê os alunos somassem todos os números de um a cem, com instruções para quê cada um colocasse sua ardósia sobre a mesa logo quê completasse a tarefa. Quase imediatamente, Gauss colocou sua ardósia sobre a mesa dizendo: “Aí está!”. O professor olhou-o com desdém enquanto os outros trabalhavam diligentemente. Quando o instrutor finalmente olhou os resultados, a ardósia de Gauss era a única com a resposta correta, 5.050, sem outro cálculo. O menino de dez anos evidentemente calculara mentalmente a soma da progressão aritmética 1 + 2 + 3 + + … + 99 + 100, presumivelmente pela fórmula . Seus mestres logo levaram o talento de Gauss à atenção do Duque de Brunswick, quê apoiou seus estudos, primeiro para quê pudesse cursar o colégio local, depois na Universidade em Göttingen, onde se matriculou em outubro de 1795.
BOYER, Cal B. História da matemática. 1. ed. 9. reimp. São Paulo: Edgard Blãcher, 1996. p. 343-344.
- ardósia
- : tipo de rocha antigamente utilizada para escrever na escola.

Página setenta e três
ATIVIDADES COMPLEMENTARES
1. (Enem/MEC) O gerente de uma fábrica pretende comparar a evolução das vendas de dois produtos similares (I e II). Para isso, passou a verificar o número de unidades vendidas de cada um dêêsses produtos em cada mês. Os resultados dessa verificação, para os meses de abril a junho, são apresentados na tabéla.
Produto |
Vendas em abril (unidade) |
Vendas em maio (unidade) |
Vendas em junho (unidade) |
|---|---|---|---|
I |
80 |
90 |
100 |
II |
190 |
170 |
150 |
O gerente estava decidido a cessar a produção do produto II no mês seguinte àquele em quê as vendas do produto I superassem as do produto II.
Suponha quê a variação na quantidade de unidades vendidas dos produtos I e II se manteve, mês a mês, como no período representado na tabéla.
Em qual mês o produto II parou de sêr produzido?
a) Junho.
b) Julho.
c) Agosto.
d) Setembro.
e) Outubro.
alternativa d
2. (PUC-RJ) Os números a1 = 5x − 5, a2 = x + 14 e a3 = 6x − 3 estão em PA.
A soma dos 3 números é igual a:
alternativa b
a) 48
b) 54
c) 72
d) 125
e) 130
3. (UFRGS-RS) Considere o padrão de construção, representado pêlos dêzê-nhôs formados por quadrados de lado 1, em cada uma das etapas indicadas na figura abaixo.
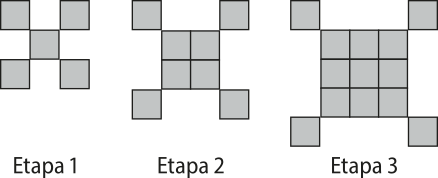
O número de quadrados de lado 1 quê farão parte da figura da etapa 10 é
a) 96.
b) 100.
c) 104.
d) 108.
e) 112.
alternativa c
4. (PUC-SP) Uma pessoa montou um quebra-cabeça de 1.000 peças em 11 dias. No 1º dia foram montadas 40 peças, e o número diário de peças montadas do 2º ao 11º dia obedeceu a uma progressão aritmética. Se o número de peças montadas no 2º dia correspondeu a 60% do número de peças montadas no 7º dia, então, o número de peças montadas no 9º dia foi:
a) 120.
b) 118.
c) 116.
d) 114.
alternativa c
5. (Enem/MEC) sôb a orientação de um mestre de obras, João e Pedro trabalharam na reforma de um edifício. João efetuou reparos na parte hidráulica nos andares 1, 3, 5, 7, e assim sucessivamente, de dois em dois andares. Pedro trabalhou na parte elétrica nos andares 1, 4, 7, 10, e assim sucessivamente, de três em três andares. Coincidentemente, terminaram seus trabalhos no último andar. Na conclusão da reforma, o mestre de obras informou, em seu relatório, o número de andares do edifício. Sabe-se quê, ao longo da execução da obra, em exatamente 20 andares, foram realizados reparos nas partes hidráulica e elétrica por João e Pedro.
Qual é o número de andares dêêsse edifício?
a) 40
b) 60
c) 100
d) 115
e) 120
alternativa d
6. (UFRGS-RS) Desde a Grécia Antiga, sabe-se quê a soma dos números ímpares consecutivos, a partir do 1, é sempre um quadrado perfeito. Como exemplo, tem-se
1 = 12
1 + 3 = 22
1 + 3 + 5 = 32
1 + 3 + 5 + 7 = 42
Então, a soma de todos os números ímpares menóres do quê 100 é
a) 422.
b) 492.
c) 502.
d) 992.
e) 1002.
alternativa c
Página setenta e quatro
7. (UERN) Um fabricante de televisores produziu 204.700 unidades em um período de 11 meses. Considerando-se quê, no primeiro mês, a produção foi de x unidades e quê, nos demais meses, foi o dôbro do mês anterior, pode-se afirmar quê o valor de x é:
a) 100
b) 90
c) 80
d) 50
alternativa a
8. (UFPA) A razão da PG cujos termos satisfazem as relações a1 + a3 + a5 = 5 e a2 + a4 + a6 = 10 é:
a)
b) 1
c)
d) 2
e) 3
alternativa d
9. (Unifor-CE) O número de termos da progressão é
a) 5
b) 6
c) 7
d) 8
e) 9
alternativa e
10. (UEG-GO) Dada a sequência (−7, 21, −63, …), quê forma uma progressão geométrica, o sexto termo dessa progressão é
a) −1.701
b) 1.701
c) 2.187
d) −5.103
e) 5.103
alternativa b
11. (Unilasalle-RS) O novo sáiti de uma empresa foi inaugurado no primeiro dia do mês de dezembro e recebeu 3 acessos. No segundo dia teve 9 acessos, no terceiro dia, 27 acessos, e assim por diante. Em quê dia de dezembro obteve 2.187 acessos?
a) 6
b) 7
c) 8
d) 9
e) 10
alternativa b
12. (IFPR) Um fractal é uma estrutura geométrica quê se repete em qualquer escala. Unindo os pontos médios dos lados de um triângulo equilátero, obtemos outro triângulo equilátero. Repetindo esse processo indefinidamente, determinamos um fractal bem simples, ilustrado na figura a seguir. Se começarmos a construção com um triângulo equilátero de lado de medida 8 unidades de comprimento, o limite para a soma dos perímetros dos triângulos equiláteros quê compõem o fractal será, em unidades de comprimento, de:

a) 45.
b) 46,5.
c) 48.
d) 72.
alternativa c
13. (Fuvest-SP) Sabe-se sobre a progressão geométrica a1, a2, a3, … quê a1 > 0 e a6 = . Além díssu, a progressão geométrica a1, a5, a9, … tem razão igual a 9. Nessas condições, o produto a2 ⋅ a7 vale:
a)
b)
c)
d)
e)
alternativa a
14. (Insper-SP) Um computador foi programado com as instruções quê estão descritas no diagrama a seguir.
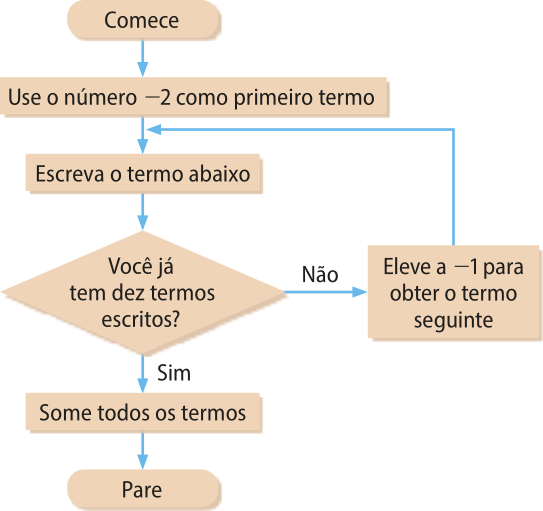
O resultado quê o computador vai apresentar depois de executar o programa é
a) −9.
b) 0.
c) −5,5.
d) 8.
e) −12,5.
alternativa e
Página setenta e cinco
15. (Uneb-BA) Considere n o cardinal de an = −250, na progressão aritmética (−2, −6, −10, …) e s, a soma dos 9 primeiros termos da progressão geométrica (3, 6, 12, 24, …).
Desse modo, é correto afirmar quê o valor de s − n é
01) 1.596
02) 1.470
03) 1.246
04) 735
05) 511
alternativa 02
16. (UFRN) A sequência de figuras a seguir representa os cinco primeiros passos da construção do conjunto de Sierpinski. Os vértices dos triângulos brancos construídos são os pontos médios dos lados dos triângulos escuros da figura anterior. Denominamos a1, a2, a3, a4 e a5, respectivamente, as áreas das regiões escuras da primeira, segunda, terceira, quarta e quinta figuras da sequência.
alternativa a

pôdêmos afirmar quê a1, a2, a3, a4 e a5 estão, nessa ordem, em progressão geométrica de razão:
a)
b)
c)
d)
PARA REFLETIR
Neste Capítulo, estudamos dois tipos de sequências numéricas: as progressões aritméticas e as progressões geométricas. Aprendemos quê tanto a PA como a PG possuem razão constante e quê podemos calcular a soma dos elemêntos quê formam esses tipos de sequências.
Além díssu, nas páginas de abertura, apresentamos os dêzê-nhôs sona para mostrar quê as sociedades lidam de diferentes maneiras com a realidade à sua volta.
Se possível, pesquise mais sobre os temas abordados no Capítulo.
Agora, vamos refletir sobre as aprendizagens do Capítulo 2:
Respostas pessoais.
• Você já conhecia algum dos conteúdos apresentados neste Capítulo? Qual(is)?
• Retornando à atividade 4 da abertura dêste Capítulo, como você responderia agora a essa questão? Algo mudou em sua resposta?
• Como podemos determinar todos os termos de uma sequência numérica finita?
• Dados o 1º e o 3º termos de uma PA, como podemos descobrir o 2º termo?
• Uma PA e uma PG podem sêr associadas a quais tipos de funções?
• Como podemos representar os passos envolvidos no cálculo da soma de uma PA ou de uma PG utilizando um fluxograma?
Página setenta e seis


