CAPÍTULO
5
RAZÕES TRIGONOMÉTRICAS NA CIRCUNFERÊNCIA
As rodas-gigantes são construções voltadas ao lazer e, por causa de suas dimensões, sérvem também como mirantes em cidades e parques de diversões em diversos locais do mundo. A primeira roda-gigante foi inaugurada em 1893 em Chicago, nos Estados Unidos. Desde então, muitas outras foram construídas, como a roda Ain Dubai, inaugurada em 2021, em Dubai, nos Emirados Árabes, com 250 metros de altura, quê passou a sêr a maior roda-gigante do mundo. A maior roda-gigante da América Látína é a Roda Rico, em São Paulo, quê se destaca com seus 91 metros de altura.
Para realizar alguns cálculos envolvendo rodas-gigantes, como determinar a distância quê certa cabine de uma roda-gigante se encontra do solo ou o comprimento do trajeto percorrido por uma cabine ao dar uma volta completa, podem-se usar conceitos quê estudaremos neste Capítulo, como arcos de circunferência e razões em uma circunferência trigonométrica.
Fontes dos dados: DEURSEN, Felipe vã. Roda-gigante surgiu há 400 anos e sofreu influências até da Torre Eiffel. Nossa UOL, [s. l.], 23 fev. 2022. Disponível em: https://livro.pw/gnzev. Acesso em: 2 out. 2024.
BRASIL. Ministério do Turismo. Maior roda-gigante da América Látína é inaugurada em São Paulo. Brasília, DF: MT, 12 dez. 2022. Disponível em: https://livro.pw/kzrxw. Acesso em: 2 out. 2024.
![]() Agora reúna-se a um colega, e façam o quê se pede em cada questão.
Agora reúna-se a um colega, e façam o quê se pede em cada questão.
1. Vocês já andaram de roda-gigante? Em caso afirmativo, conversem sobre como foi essa experiência.
Resposta pessoal.
2. Suponham quê uma pessoa está em uma cabine no ponto mais baixo da roda-gigante. Quantos graus a roda deve girar para quê essa pessoa fique no ponto mais alto?
180°
3. Se uma cabine de uma roda-gigante dá cinco voltas completas, quantos graus, ao todo, essa cabine percorreu?
5 ⋅ 360° = 1.800°
4. Expliquem o quê são e quais são as relações entre arcos, ângulos centrais e ângulos inscritos em uma circunferência.
4. Espera-se quê os estudantes respondam quê: arco é uma parte de uma circunferência; ângulo central é o ângulo cujo vértice é o centro de uma circunferência; ângulo inscrito é aquele em quê os seus lados são secantes à circunferência e o seu vértice é um ponto da circunferência. Espera-se quê os estudantes mencionem as seguintes relações: a medida angular de um arco de circunferência é igual à medida do ângulo central correspondente, e a medida de um ângulo inscrito na circunferência é a mêtáde da medida do ângulo central.
Página cento e quarenta e sete

Página cento e quarenta e oito
Introdução
Nesta Coleção, estudamos as razões trigonométricas seno, cosseno e tangente para o triângulo retângulo. No entanto, ao estudar os fenômenos periódicos, precisamos ampliar esse conceito para outros ângulos fora do intervalo entre 0° e 90° para, então, realizar a modelagem por meio das funções trigonométricas, assunto do Capítulo 6 dêste Volume.
Sendo assim, serão apresentados alguns conceitos novos, como as razões trigonométricas na circunferência, quê permitem o cálculo dessas razões para qualquer ângulo, inclusive para os ângulos maiores do quê 90°.
Agora, vamos retomar alguns conceitos da Geometria quê serão aplicados nesse estudo.
Arcos de circunferência
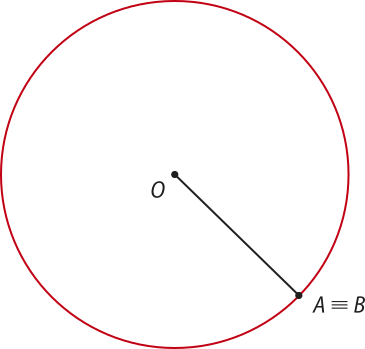
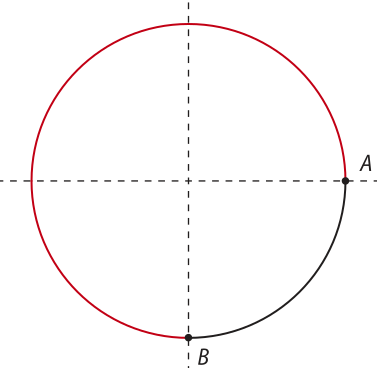
Ao marcarmos dois pontos A e B em uma circunferência de centro O, ela fica dividida em duas partes denominadas arcos de circunferência ou, simplesmente, arcos. Os pontos A e B são as extremidades dos arcos e, portanto, pertencem a ambos.
Os pontos A e B determinam dois arcos de circunferência quê podem sêr indicados por . Quando não ficar evidente a qual arco estamos nos referindo, podemos inserir um ponto entre as extremidades A e B e utilizar a notação ou para identificar cada arco.
Se as extremidades A e B coincidem, um dos arcos fica reduzido a um ponto e o outro é a própria circunferência. Eles são chamados, respectivamente, de arco nulo e de arco de uma volta.
Quando as extremidades correspondem às extremidades de um diâmetro, teremos duas semicircunferências ou arcos de meia-volta.



Página cento e quarenta e nove
Ângulo central
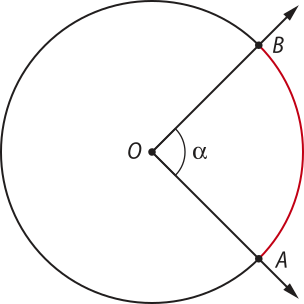
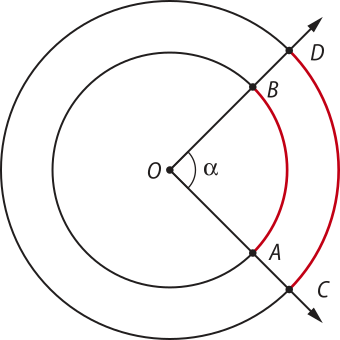
Todo ângulo quê tem vértice no centro da circunferência é chamado de ângulo central. Assim, todo arco de circunferência tem um ângulo central quê é correspondente a ele.
Na figura a seguir, é o ângulo central correspondente ao arco . Além díssu, med() = (alfa)".
Acompanhe alguns exemplos a seguir.
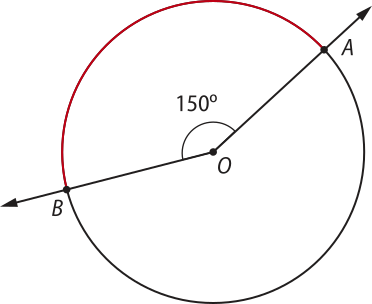
a) O ângulo central indicado méde 150°.
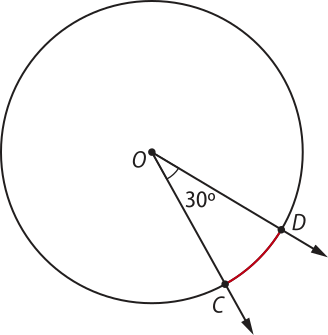
b) O ângulo central indicado méde 30°.
Medida angular e comprimento de arcos de circunferência
A medida angular de um arco é a medida do ângulo central correspondente.
Por exemplo, na figura a seguir, a medida angular do arco é igual a (alfa)". Também podemos representá-la por med(). Observe quê a medida angular do arco também é (alfa)".
A medida linear de um arco é o comprimento ao longo do arco, ou seja, a medida de uma extremidade a outra.
Saiba quê...
Quando dizemos apenas medida de um arco, geralmente nos referimos à medida angular do arco.
Pense e responda
O comprimento de um arco depende do raio da circunferência em quê ele está? E a medida angular de um arco? Justifique.
sim; não
Ver as Orientações para o professor
Página cento e cinquenta
Unidades de medida de arcos de circunferência
A medida de um arco de circunferência póde sêr expressa em grau ou em radiano. Provavelmente, você já estudou a unidade de medida grau em anos escolares anteriores. Vamos retomar algumas ideias relacionadas a essa unidade de medida e, em seguida, apresentar o radiano.
Grau
Ao dividir uma circunferência em 360 partes iguais, cada parte ôbitída é um arco quê corresponde a da circunferência e tem medida angular 1 grau, quê é indicado por 1°. Assim, uma circunferência tem 360°.
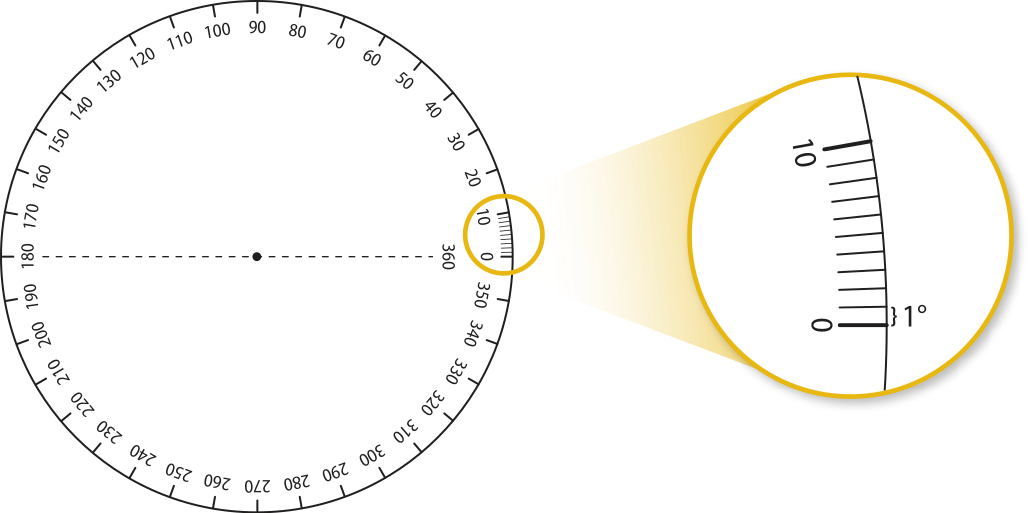
Os arcos de 90°, 180° e 270°, marcados em sentido anti-horário nas figuras a seguir, representam um quarto, mêtáde e três quartos da circunferência, respectivamente, pois , e .
Os submúltiplos do grau são o minuto e o segundo, dado quê:
• um minuto (1(minutos)") é igual a do grau;
• um segundo (1(segundos)") é igual a do minuto.
Pense e responda
• Um grau corresponde a quantos minutos?
60 minutos
• Um minuto corresponde a quantos segundos?
60 segundos
• Um grau corresponde a quantos segundos?
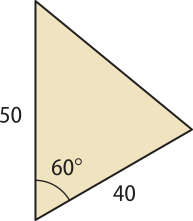
3.600 segundos
Página cento e cinquenta e um
Radiano
Agora, vamos conhecer outra unidade de medida angular: o radiano.
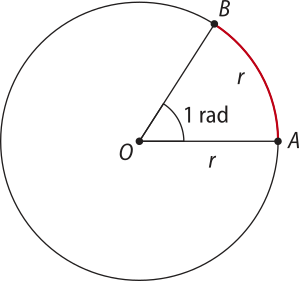
A medida de um arco é igual a 1 radiano (1 rad) quando o comprimento da sua medida linear é igual ao comprimento do raio da circunferência quê o contém.

Observe o arco a seguir.
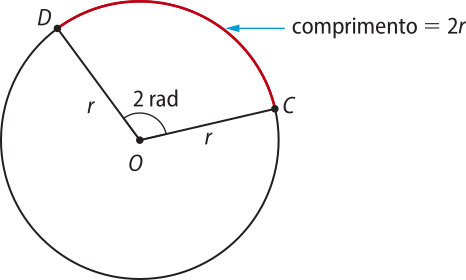
O comprimento do arco méde o dôbro da medida do raio, então a medida angular do arco é 2 rad.
Saiba quê...
• Assim como a medida do arco o ângulo central também méde 1 rad.
• Do mesmo modo, o ângulo central , assim como o arco também méde 2 rad.
Pense e responda
• Qual é a medida de um arco cujo comprimento é o triplo da medida do raio da circunferência correspondente?
3 rad
• Qual é o comprimento de um arco contido em uma circunferência de raio r cujo ângulo central correspondente méde 5 radianos?
5r
• Qual é o comprimento de um arco contido em uma circunferência de raio r cujo ângulo central correspondente méde x radianos?
x ⋅ r
• Um radiano equivale a aproximadamente quantos graus? Utilizando um transferidor, meça, na figura anterior desta página, o ângulo central Be verifique.
aproximadamente 57°
Relação entre grau e radiano
Como converter um ângulo medido em grau para a sua equivalência em radiano? No Ensino Fundamental, você estudou quê o comprimento de uma circunferência de raio r é dado por 2(pi)"r. Agora, vamos usar essa informação para estabelecer a relação entre grau e radiano e fazer conversões entre as unidades de medida angular.
Dada uma circunferência de raio r, o seu comprimento C é C = 2(pi)"r. pôdêmos interpretar essa expressão como o raio r quê "cabe" 2(pi)" vezes nesse comprimento, ou seja, aproximadamente 6,28 vezes.
Como cada arco de comprimento igual a r corresponde a um ângulo central de medida 1 rad, então o arco de comprimento 2(pi)"r (a circunferência toda) corresponde a um ângulo central de medida 2(pi)" rad. Sabemos quê a circunferência tem 360°, então concluímos quê:
2(pi)" rad = 360°
Página cento e cinquenta e dois
Pense e responda
Que cálculos podemos fazer mentalmente para obtêr as relações apresentadas a partir da relação 2(pi)" rad = 360°?
Ver as Orientações para o professor.
A partir dessa relação, podemos escrever outras, por exemplo:
• (pi)" rad = 180°
• rad = 90°
• rad = 45°
Utilizando uma regra de três e a relação (pi)" rad = 180°, podemos converter em radiano qualquer medida angular expressa em grau e vice-versa. Por exemplo, para escrever 270° em radiano, fazemos:

Então: x = rad
Logo, 270° equivalem a radianos.
Acompanhe, agora, alguns exemplos para determinarmos o comprimento e a medida angular de alguns arcos.
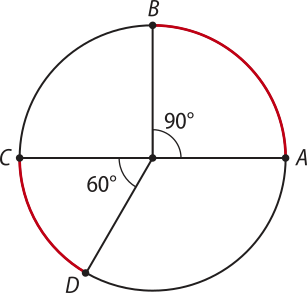
Na circunferência de raio r a seguir, os arcos e médem, respectivamente, 90° e 60°. Vamos expressar essas medidas em radiano e determinar o comprimento dos arcos e .
Como a circunferência tem 360°, o comprimento do arco é a quarta parte do comprimento da circunferência, e o comprimento do arco é a sexta parte do comprimento da circunferência. Assim, para determinar o comprimento do arco, dividimos 2(pi)"r (comprimento da circunferência) por quatro e por seis, respectivamente, como indicado a seguir.
Ângulo (em grau) |
Ângulo (em radiano) |
Comprimento do arco |
|
|---|---|---|---|
Circunferência completa |
360° |
2(pi)" |
2(pi)"r |
Arco |
90° |
2(pi)"r = |
|
Arco |
60° |
2(pi)"r = |
Pense e responda
Utilizando uma calculadora e a relação (pi)" rad = 180°, determine, aproximada mente, em grau, o valor de 1 rad.
aproximadamente 57,29°
De modo geral, para calcular o comprimento (éli)" de um arco de medida (alfa)" em uma circunferência de raio r, usamos a regra de três e estabelecemos as seguintes relações:
• para (alfa)" em grau

• para (alfa)" em radiano
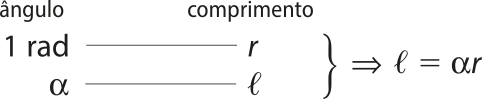
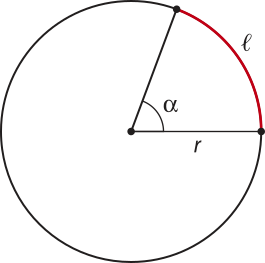
Saiba quê...
Quando a unidade de medida angular não estiver explicitada, consideraremos quê está em radiano. Por exemplo, corresponde a rad.
Página cento e cinquenta e três
ATIVIDADES RESOLVIDAS
1. Expresse 22°30(minutos)" em radiano.
Resolução
Primeiro, vamos converter 22°30(minutos)" para minuto: 22°30(minutos)" = 22 ⋅ 60(minutos)" + 30(minutos)" = 1.320(minutos)" + 30(minutos)" = 1.350(minutos)"
Agora, vamos converter 180° para minuto: 180° = 180 ⋅ 60(minutos)" = 10.800(minutos)"
Assim, podemos fazer a seguinte regra de três:
![]() ⇒ ⇒ 8x = (pi)" rad ⇒ x = rad
⇒ ⇒ 8x = (pi)" rad ⇒ x = rad
Também podemos resolver de outro modo. Acompanhe:
Como 30 minutos equivalem a meio grau, temos 22°30(minutos)" = 22,5°.
Seja x a medida do arco, temos:
x = 22,5° ⇒ 2x = 45° ⇒ 4x = 90° ⇒ 4x = rad⇒x = rad
Logo, 22°30(minutos)" = rad.
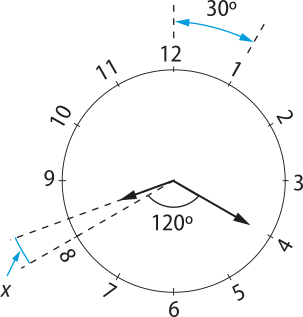
2. Determine, em grau, a medida do menor ângulo formado pêlos ponteiros de um relógio às 8h20min.
Resolução
Sejam (alfa)" a medida do ângulo pedido e x a medida do ângulo descrito pelo ponteiro das horas em 20 min a partir das 8 h. O mostrador do relógio é dividido em 12 arcos iguais. Por isso, o arco compreendido entre dois números consecutivos do relógio méde , ou seja, 30°. Assim, (alfa)" = x + 120°, já quê 120° é o ângulo formado pelo arco com extremidade nos números 4 e 8 do relógio.
A cada 60 minutos, o ponteiro das horas percórre 30°. Então, podemos fazer a seguinte relação:
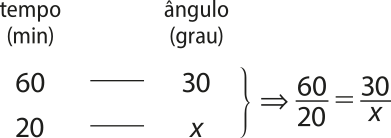 ⇒ 3 = ⇒ x = 10 (medida em grau)
⇒ 3 = ⇒ x = 10 (medida em grau)
(alfa)" = x + 120° ⇒ (alfa)" = 10° + 120° ⇒ (alfa)" = 130°
Portanto, o ângulo solicitado méde 130°.
ATIVIDADES
1. Expresse:
a) 60° em radiano;
rad
b) 210° em radiano;
rad
c) rad em grau;
200°
d) rad em grau.
9°
2. Em uma circunferência de 32 cm de diâmetro, marca-se um arco de 8 cm de comprimento. Qual é a medida dêêsse arco em radiano?
0,5 rad
3. Qual é, em radiano, a medida do arco descrito pelo ponteiro dos minutos de um relógio em um período de 25 minutos?
rad
• ![]() Reúna-se a um colega e expliquem um ao outro o raciocínio utilizado para resolver a atividade. Vocês resolveram da mesma maneira?
Reúna-se a um colega e expliquem um ao outro o raciocínio utilizado para resolver a atividade. Vocês resolveram da mesma maneira?
Resposta pessoal.
Página cento e cinquenta e quatro
4. Na figura, têm-se três circunferências, de centros A, B e C, tangentes duas a duas. As retas e são perpendiculares. Sendo 4 m o raio da circunferência maior, quantos metros devemos percorrer para ir de P a Q, seguindo as flechas?
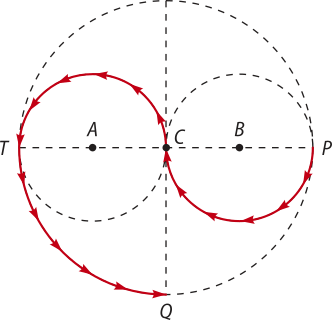
6(pi)" metros
5. Luana é artesã e faz bordados em bastidor. Para estimar a quantidade de linha quê usará na próxima encomenda, ela precisa saber algumas medidas do desenho bordado. Ajude Luana e determine o comprimento do contôrno de cada detalhe indicado em azul nas figuras dos itens a seguir. Use (pi)" = 3,14.

a) 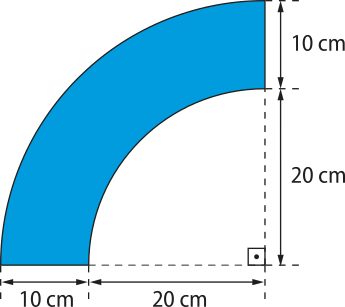
98,5 cm
b) Para fazer um detalhe, Luana desenhou um quadrado ABCD de lado 10 cm. Em seguida, traçou as linhas curvas, quê são semicircunferências com centros nos pontos médios, M e N, dos lados do quadrado.

51,4 cm
6. Você conhece o relógio de pêndulo? Ele foi criado pelo físico holan-dêss crístian Huygens (1629-1695) em 1656 a partir do princípio de funcionamento desenvolvido por Galileu Galilei. Uma das peças principais dêêsse tipo de relógio é o pêndulo, responsável por manter o equipamento funcionando.
Fonte dos dados: FERREIRA, Eduardo S. O relógio cicloidal de Huygens. Campinas: Instituto de Matemática, Estatística e Computação Científica (Imecc-Unicamp), [201-].
Disponível em: https://livro.pw/luwkg. Acesso em: 10 out. 2024.
Suponha quê o pêndulo de um relógio tenha comprimento 0,5 m e execute o movimento de A para B indicado na figura. Determine o comprimento do arco quê a extremidade do pêndulo descreve.
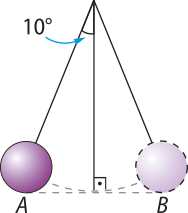
m
7. (OBMEP) Duas formigas partem do ponto A e vão até o ponto D, andando no sentido indicado pelas flechas. A primeira percórre o semicírculo maior; a segunda, o segmento , o semicírculo menor e o segmento . Os pontos A, B, C e D estão alinhados e os segmentos e médem 1 cm cada um. Quantos centimetros a segunda formiga andou menos quê a primeira?
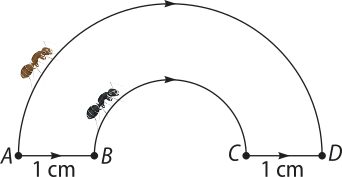
a) 2
b) (pi)"
c)
d) (pi)" − 2
e) 2(pi)"
alternativa d
Página cento e cinquenta e cinco
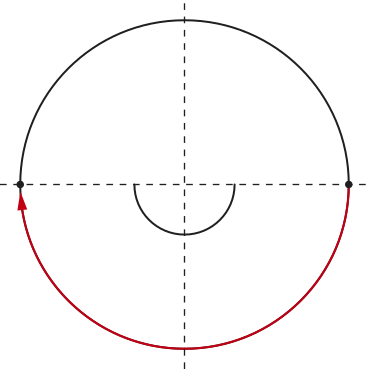
Circunferência orientada
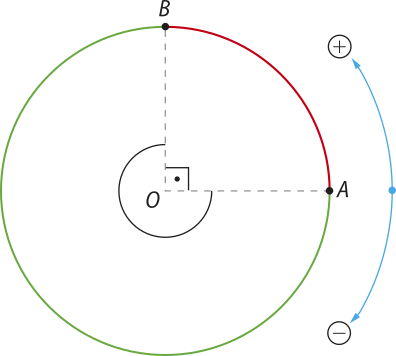
A figura a seguir mostra quê, sobre a circunferência, o percurso de A para B póde sêr feito no sentido anti-horário, seguindo o arco vermelho ou no sentido horário, seguindo o arco vêrde .
Ao estabelecer o sentido anti-horário do percurso como positivo e o sentido horário como negativo, temos uma circunferência orientada.
Assim, podemos ter as seguintes medidas angulares para o percurso de A para B da figura.
• arco vermelho: med() = rad ou med () = 90°
• arco vêrde: med() = rad ou med () = −270°
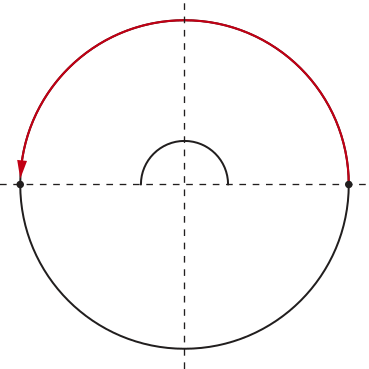
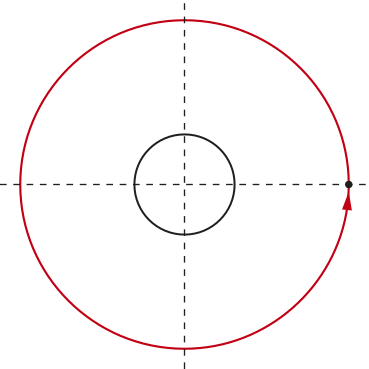
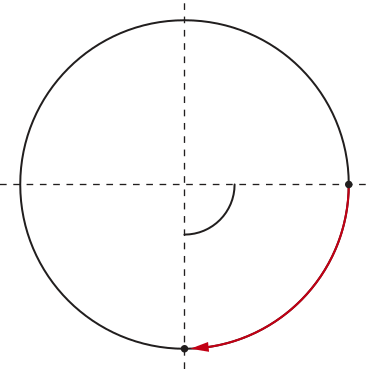
Acompanhe outros exemplos de arcos medidos na circunferência orientada:
• no sentido anti-horário

• no sentido horário
Página cento e cinquenta e seis
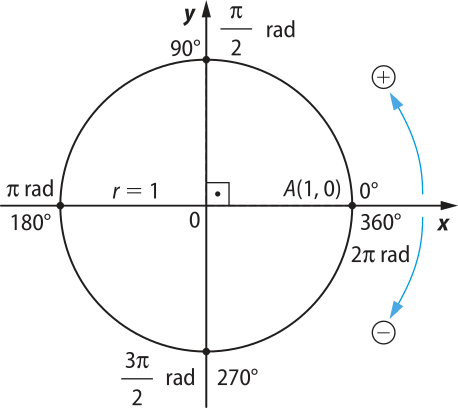
Circunferência trigonométrica
Vamos, agora, fixar um sistema de coordenadas cartesianas ortogonais xOy no plano.
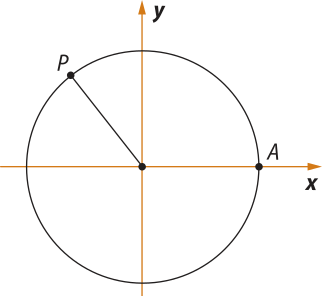
A circunferência orientada de centro na origem do sistema de coordenadas cartesianas de raio unitário (r = 1) é denominada circunferência trigonométrica ou ciclo trigonométrico. Os arcos da circunferência trigonométrica terão origem no ponto A(1, 0), denominado origem dos arcos. Observe a figura 1 a seguir.
Os eixos x e y do sistema de coordenadas cartesianas determinam, no plano, quatro regiões, denominadas quadrantes. Os quadrantes são numerados no sentido anti-horário a partir do ponto A. Os pontos A, B, C e D estão nos eixos e não pertencem a quadrante algum. Observe a circunferência trigonométrica na figura 2, com a indicação das coordenadas dos pontos A, B, C e D e a indicação dos quadrantes.

Saiba quê...
Observe quê, para todo ponto (x, y) pertencente à circunferência trigonométrica, temos: −1 ≤ x ≤ 1 e −1 ≤ y ≤ 1.
Arcos kôn-gru-us
No início do Capítulo, comentamos quê vamos estudar as razões trigonométricas para qualquer ângulo. Para isso, precisamos compreender como localizá-los na circunferência trigonométrica. Por exemplo, como representar um arco de 450° na circunferência trigonométrica? É o quê acompanharemos a seguir.
Seja P um ponto da circunferência trigonométrica. pôdêmos verificar quê há uma infinidade de arcos com origem em A e extremidade em P. Para isso, basta, a partir de P, dar voltas completas, ou seja, dar voltas em arcos cujas medidas sêjam múltiplas de 2(pi)", em qualquer sentido, horário ou anti-horário.
Considerando como exemplo o arco , mostrado na figura, o primeiro arco de quê nos lembramos é o de medida . No entanto, o ponto P é a extremidade de outros arcos, quê podem sêr obtidos adicionando (ou subtraindo) múltiplos inteiros de 2(pi)" a .
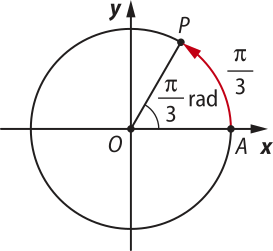
Pense e responda
por quê os arcos múltiplos de 2(pi)" têm a mesma extremidade?
Porque 2(pi)" é o comprimento da circunferência trigonométrica, quê tem raio unitário.
Página cento e cinquenta e sete
Observe os exemplos:
• No sentido anti-horário, ao dar uma volta completa mais , obtemos o arco de medida , pois = ( +1 ⋅ 2(pi)").
• No sentido anti-horário, ao dar duas voltas completas mais , obtemos o arco de medida , pois =( + 2 ⋅ 2(pi)").
• No sentido horário, ao dar uma volta completa menos obtemos o arco de medida pois = ( − 1 ⋅ 2(pi)").
Saiba quê...
Poderíamos considerar a medida do arco em grau; nesse caso, para obtêr arcos com extremidade em P, bastaria adicionar (ou subtrair) múltiplos inteiros de 180°.
Como = 60°, teríamos, entre outros arcos:
• 60° + 1 ⋅ 360° = 420°
• 60° + 2 ⋅ 360° = 780°
• 60° − 1 ⋅ 360° = −300°
Os arcos quê têm a mesma extremidade P são chamados de arcos kôn-gru-us ou congruentes.
O arco de medida θ, com 0° < θ < 360°, ou 0 < θ < 2(pi)", é chamado de 1ª determinação positiva dos arcos kôn-gru-us a ele, pois é o único representante dêêsses arcos kôn-gru-us quê está na primeira volta positiva.
De modo geral, um arco quê méde (alfa)" radianos e cuja primeira determinação positiva méde θ tem como expressão geral dos arcos kôn-gru-us a ele:
θ + k ⋅ 2(pi)", com k ∈ ℤ ou θ + 2k(pi)", com k ∈ ℤ
Caso a medida do arco seja dada em grau, como a circunferência tem 360°, teremos:
θ + k ⋅ 360°, com k ∈ ℤ
Pense e responda
• Qual é o arco obtído quando k = 0 na expressão dos arcos kôn-gru-us?
A 1ª determinação positiva dos arcos kôn-gru-us ao arco considerado.
• O quê acontece quando k é um valor negativo?
Deve-se percorrer a circunferência no sentido horário para obtêr a extremidade do arco.
• Qual é o arco côngruo a na segunda volta negativa? Como você raciocinou para chegar à resposta?
. Resposta pessoal. Para chegar a essa conclusão, os estudantes podem substituir k = −2 na expressão geral dos arcos kôn-gru-us.
Página cento e cinquenta e oito
Acompanhe um exemplo de como determinar a expressão geral dos arcos kôn-gru-us ao arco de 1.940°. Inicialmente, precisamos determinar a medida da 1ª determinação positiva dêêsse arco. Vamos dividir 1.940° por 360° para determinar quantas voltas completas o arco dará na circunferência trigonométrica.
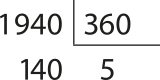
Assim, podemos escrever: 1.940° = 140° + 5 ⋅ 360°
140° ← 1ª determinação positiva
5 ← número de voltas completas
Portanto, a expressão geral dos arcos kôn-gru-us ao arco de 1.940° é:
140° + k ⋅ 360°, com k ∈ ℤ

Números reais associados a pontos da circunferência trigonométrica
Estudamos quê, além da origem A, cada arco da circunferência trigonométrica tem, como outra extremidade, um único ponto na circunferência. Assim, é possível indicar um arco apenas por esse ponto.
Vamos, agora, associar cada número real (alfa)" a um único ponto P na circunferência trigonométrica, dado quê:
• se (alfa)" > 0, percorremos, a partir de A e em sentido anti-horário, um arco de comprimento (alfa)" com extremidades em A e P;
• se (alfa)" < 0, percorremos, a partir de A e em sentido horário, um arco de comprimento |(alfa)"| com extremidades em A e P;
• se (alfa)" = 0, o ponto P coincide com o ponto A.
É como se "enrolássemos" a reta real na circunferência trigonométrica, com os pontos associados aos números positivos no sentido anti-horário e com os pontos associados aos números negativos no sentido horário. A origem da reta real coincide com o ponto A.
Acompanhe dois exemplos:
a) Para localizar o ponto associado ao número , partimos de A e percorremos um arco de comprimento na circunferência no sentido anti-horário.
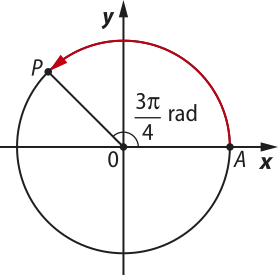
• (alfa)" =
• med() =
b) Para localizar o ponto associado ao número quê é negativo, percorremos um arco de comprimento no sentido horário na circunferência a partir de A.
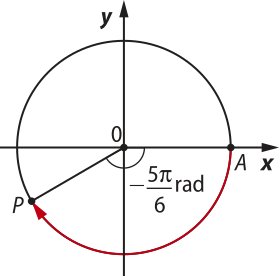
• (alfa)" =
• med() =
Saiba quê...
Como a circunferência trigonométrica tem raio unitário, cada arco associado a um número real (alfa)" tem comprimento e medida angular (alfa)" rad.
Página cento e cinquenta e nove
ATIVIDADES RESOLVIDAS
3. escrêeva a expressão geral dos arcos kôn-gru-us aos arcos a seguir.
a)
b) 175°
Resolução
a) A expressão geral para arcos em radiano é θ + 2k(pi)". Substituindo θ por , já quê 0 < < 2(pi)", temos: + 2k(pi)", com k ∈ ℤ.
b) A expressão geral para arcos em grau é θ + k ⋅ 360°. Substituindo θ por 175°, já quê 0° < 175° < 360°, temos: 175° + k ⋅ 360°, com k ∈ ℤ.
4. Um móvel percorreu um arco de 1.690° na circunferência trigonométrica, partindo do ponto A, origem dos arcos. Quantas voltas completas na circunferência esse móvel deu? Em qual quadrante parou?
Resolução
Para determinar o número de voltas completas, vamos dividir a medida do arco, em grau, por 360°, quê é a medida de uma volta na circunferência. Assim:
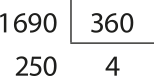
Com isso, podemos escrever a seguinte expressão:
1.690° = 250° + 4 ⋅ 360°
250° ← O arco de 1.690° tem a mesma extremidade quê o arco de 250°.
4 ← número de voltas completas
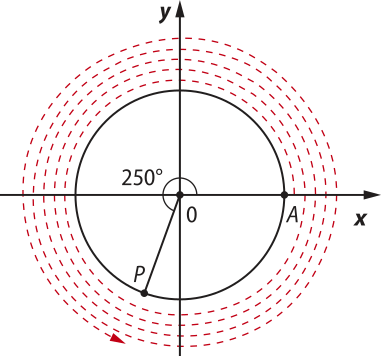
Portanto, o móvel deu quatro voltas completas no sentido anti-horário e, como 180° < 250°< 270°, parou no terceiro quadrante.
5. escrêeva a expressão geral dos arcos kôn-gru-us ao arco de .
Resolução
Temos quê:
= 17, 5(pi)" = 1, 5(pi)" + 16(pi)" = (pi)" + 8 ⋅ 2(pi)"
Assim, a 1ª determinação positiva do arco de é , e a expressão geral dos arcos kôn-gru-us é + 2k(pi)", com k ∈ ℤ.
Outra maneira de resolver a atividade seria transformar o ângulo de radiano para grau:
= 35 ⋅ = 35 ⋅ 90° = 3.150°
Assim, dividindo 3.150° por 360°, temos:
Então, podemos escrever:
3.150° = 270° + 8 ⋅ 360°
270° ← 1ª determinação positiva
8 ← número de voltas completas
Voltando para as medidas em radiano, temos:
+ 8 ⋅ 2(pi)"
Assim, a expressão geral dos arcos kôn-gru-us ao arco de é + 2k(pi)", com k ∈ ℤ.
Página cento e sessenta
ATIVIDADES
8. Represente, na circunferência trigonométrica, os pontos associados aos números a seguir.
a)
b)
c)
d) −5(pi)"
Ver as Orientações para o professor.
9. Determine a expressão geral dos arcos kôn-gru-us aos arcos destacados nas circunferências trigonométricas a seguir.
a) 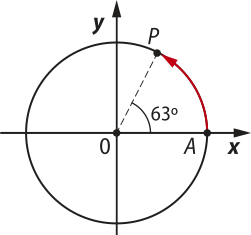
63° + k ⋅ 360°, com k ∈ ℤ
b) 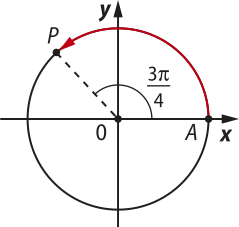
+ 2k(pi)", com k ∈ ℤ
10. Verifique se os números e estão associados a pontos coincidentes na circunferência trigonométrica.
sim
• ![]() Reúna-se a um colega e explique a ele como você fez para chegar a essa conclusão. Vocês pensaram da mesma maneira?
Reúna-se a um colega e explique a ele como você fez para chegar a essa conclusão. Vocês pensaram da mesma maneira?
Resposta pessoal.
11. Verifique se são kôn-gru-us os seguintes pares de arcos:
a) 1.490° e −1.030°
São kôn-gru-us.
b) rad e rad
Não são kôn-gru-us.
12. Determine o quadrante em quê estão localizados os pontos correspondentes aos seguintes arcos:
a) −1.640°
segundo quadrante
b) rad
quarto quadrante
13. Determine quantas voltas completas um móvel dá e em quê quadrante ele para se, partindo da origem dos arcos, percórre, na circunferência trigonométrica, um arco de:
Ver as Orientações para o professor.
a) 1.810°
b) rad
c) −1.200°
d) 900°
e) rad
f) rad
14. Quantos centimetros percórre um corpo quê descreve um arco de 600° em uma circunferência de raio 10 cm? Use (pi)" ≃ 3,14.
aproximadamente 104,67 cm
15. A figura a seguir representa um quadrado inscrito em uma circunferência trigonométrica. Determine, em grau e em radiano, as 1as determinações positivas dos arcos cujas extremidades são os vértices do quadrado.
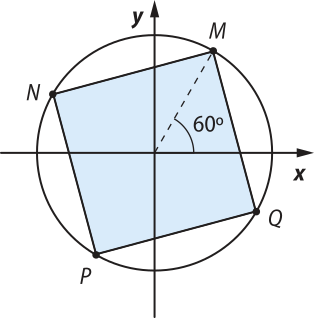
Ver as Orientações para o professor.
16. (Unicentro-PR) Analise as sentenças abaixo e assinale a alternativa correta:
I. A expressão geral dos arcos congruentes a 60° é (alfa)" = 60° + x60°; com x ∈ ℕ.
II. O menor valor não negativo côngruo ao arco de 1.140° é (alfa)" = 48°.
III. Convertendo 60° para radianos, temos rad.
IV. Na transformação de radianos para graus, encontramos 315° como resultado.
V. A expressão geral dos arcos kôn-gru-us aos arcos de 45° é 45° + k360°, com k ∈ ℤ.
a) I, II, III, IV e V são verdadeiras.
b) II, III, IV e V são verdadeiras.
c) I, II, III e V são verdadeiras.
d) III, IV e V são verdadeiras.
e) Somente II é verdadeira.
alternativa d
17. Represente, na circunferência trigonométrica, as extremidades dos arcos cujas medidas são dadas pelas expressões a seguir.
Ver as Orientações para o professor.
a) (alfa)" = + k(pi)", k ∈ ℤ
b) (alfa)" = + , k ∈ ℤ
c) (alfa)" = 90° + k ⋅ 90°, k ∈ ℤ
Página cento e sessenta e um
Seno e cosseno de um arco
Você já estudou as razões trigonométricas seno, cosseno e tangente no triângulo retângulo. Vamos retomar essas ideias.
Seja o triângulo retângulo ABC representado a seguir. Definimos seno, cosseno e tangente do ângulo agudo (alfa)" como razões entre as medidas dos lados do triângulo, como indicado a seguir.
sen (alfa)" =
cos (alfa)" =
tg (alfa)" =

Pense e responda
Nesse triângulo retângulo, sêndo med = (beta)", quais são as expressões de sen (beta)", de cos (beta)" e de tg (beta)"?
sen (beta)" = , cos(beta)"= e tg (beta)" =
Agora, vamos estudar esses conceitos na circunferência trigonométrica, estendendo-os para ângulos quaisquer.
Seja M um ponto da circunferência trigonométrica associado ao número real (alfa)". Estudamos quê M é a extremidade final do arco de medida (alfa)" em radiano. Define-se:
O seno de (alfa)" é a ordenada do ponto M.
O cosseno de (alfa)" é a abscissa do ponto M.
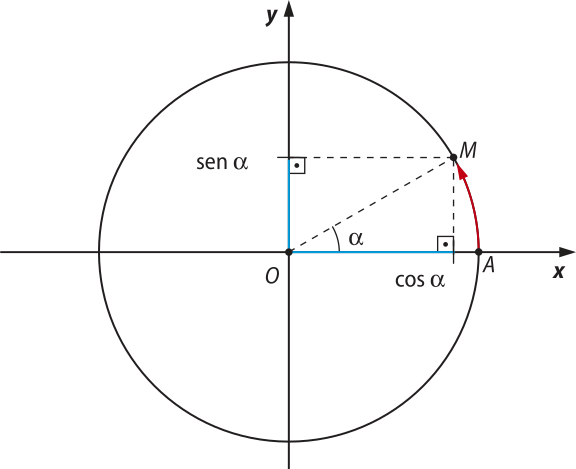
O eixo vertical y é chamado de eixo dos senos e o eixo horizontal x é chamado de eixo dos cossenos.
Com isso, cada número real (alfa)" corresponde a um ponto da circunferência trigonométrica de coordenadas (cos (alfa)", sen (alfa)").
Essas definições de seno e de cosseno são válidas para o ponto M em qualquer quadrante da circunferência trigonométrica e também para quando M está sobre os eixos. Os sinais do seno e do cosseno varíam conforme mostrado na página a seguir.
Pense e responda
Relacione a definição de seno e de cosseno no triângulo retângulo com a definição de seno e de cosseno para ângulos na circunferência trigonométrica. Justifique por quê elas coincidem para 0 ≤ (alfa)" ≤ .
Ver as Orientações para o professor.
Página cento e sessenta e dois
1) No primeiro quadrante, o seno é positivo e o cosseno é positivo.
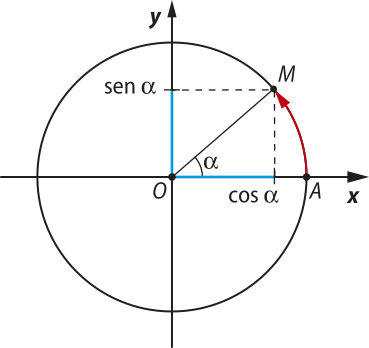
■ abscissa de M > 0 ⇒ cos (alfa)" > 0
2) No segundo quadrante, o seno é positivo e o cosseno é negativo.
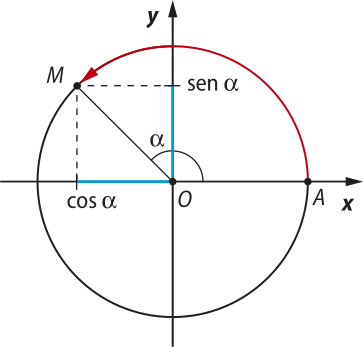
■ abscissa de M < 0 ⇒ cos (alfa)" < 0
3) No terceiro quadrante, o seno é negativo e o cosseno é negativo.
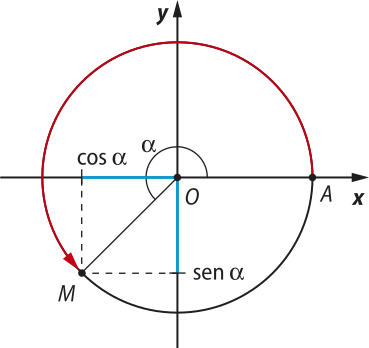
■ abscissa de M < 0 ⇒ cos (alfa)" < 0
4) No quarto quadrante, o seno é negativo e o cosseno é positivo.
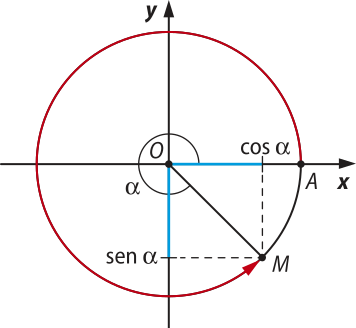
■ abscissa de M > 0 ⇒ cos (alfa)" > 0
Pense e responda
• Lembrando quê a circunferência trigonométrica tem raio unitário, responda:
a) Qual é o valor mássimo quê o seno de um ângulo póde assumir? E o valor mínimo?
1; −1
b) Qual é o valor mássimo quê o cosseno de um ângulo póde assumir? E o valor mínimo?
1; −1
• O quê acontece com os sinais do seno e do cosseno quando o ponto M está sobre o eixo x? E sobre o eixo y?
Ver as Orientações para o professor.
Alguns valores do seno e do cosseno
Agora quê já definimos o seno e o cosseno de qualquer ângulo, podemos obtêr esses valores com o uso de um software de Geometria Dinâmica, como o GeoGebra, ou utilizando uma calculadora científica. Atualmente, a maioria das calculadoras disponíveis nos sistemas operacionais dos celulares possui essa opção. No entanto, assim como foi estudado para as razões trigonométricas no triângulo retângulo, alguns ângulos são utilizados com bastante freqüência em situações nas quais não é possível recorrer a uma calculadora; portanto, saber os valores do seno e do cosseno dêêsses ângulos ajuda na realização dos cálculos.
Página cento e sessenta e três
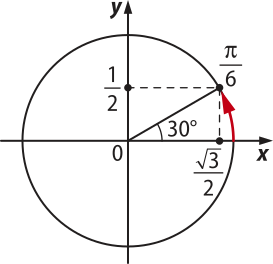
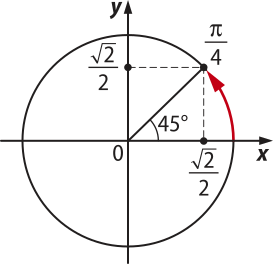
Observe o qüadro a seguir.
Medida do arco |
0° ou 0 |
30° ou |
45° ou |
60° ou |
90° ou |
180° ou (pi)" |
270° ou |
360° ou 2(pi)" |
|---|---|---|---|---|---|---|---|---|
sen |
0 |
1 |
0 |
−1 |
0 |
|||
cos |
1 |
0 |
−1 |
0 |
1 |
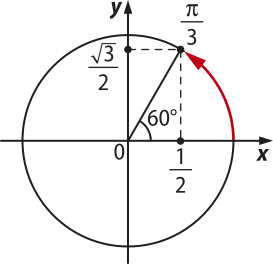
Saiba quê...
Como comentamos anteriormente, quando a unidade de medida angular do arco não estiver indicada, consideraremos quê está em radiano.
Pense e responda
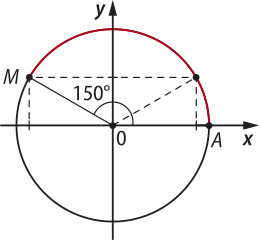
Reúna-se a um colega e discutam como vocês fariam, apenas com o qüadro anterior e seus conhecimentos matemáticos, para determinar o seno e o cosseno do arco de 150°.
Resposta pessoal.
Redução ao primeiro quadrante
A partir dos valores de seno e de cosseno para o primeiro quadrante e usando simetrias na circunferência trigonométrica, podemos estabelecer os valores de seno e de cosseno para arcos nos demais quadrantes. Ao fazer isso, dizemos quê estamos fazendo uma redução ao primeiro quadrante.
Acompanhe, a seguir, como fazer essa redução ao primeiro quadrante a partir de cada um dos demais quadrantes.
• Redução do segundo quadrante para o primeiro quadrante
Seja M o ponto da circunferência trigonométrica correspondente ao arco de medida (alfa)". O ponto N, correspondente ao arco de medida ((pi)" − (alfa)"), pertencente ao segundo quadrante, é simétrico ao ponto M em relação ao eixo dos senos.
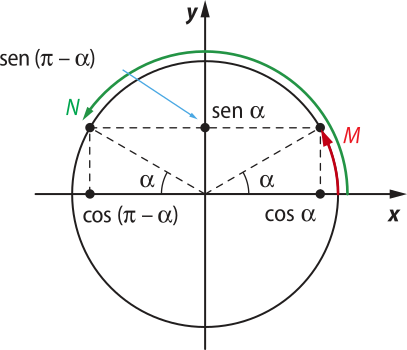
Note, na figura, quê, pela simetria, os pontos M e N têm a mesma ordenada, porém abscissas opostas. Logo, temos:
sen ((pi)" − (alfa)") = sen (alfa)"
cos ((pi)" − (alfa)") = −cos (alfa)"
Pense e responda
• por quê podemos afirmar quê cos ((pi)" − (alfa)") = −cos (alfa)"?
Dica: obissérve os tracejados quê formam triângulos na imagem.
Ver as Orientações para o professor.
• Retome a questão do Pense e responda anterior: Qual é o valor do seno e o do cosseno de 150°? Depois de estudar esse conteúdo, você pensou de maneira diferente?
Resposta pessoal.
sen (150°) = sen (30°) =
cos (150°) = −cos 30° = −
Página cento e sessenta e quatro
• Redução do terceiro quadrante para o primeiro quadrante
O ponto P, correspondente ao arco de medida ((pi)" + (alfa)"), pertencente ao terceiro quadrante, é simétrico ao ponto M, extremidade do arco de medida (alfa)", em relação ao centro da circunferência O.
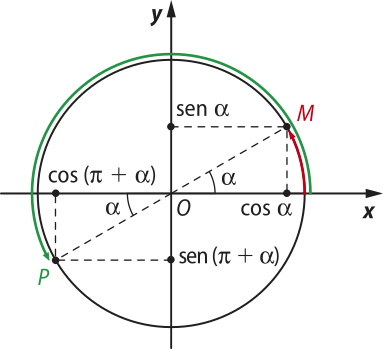
Pela simetria, os pontos M e P têm ordenadas opostas e abscissas opostas.
Logo:
sen ((pi)" + (alfa)") = −sen (alfa)"
cos ((pi)" + (alfa)") = −cos (alfa)"
• Redução do quarto quadrante para o primeiro quadrante
O ponto Q, correspondente ao arco de medida (2(pi)" − (alfa)"), pertencente ao quarto quadrante, é simétrico ao ponto M, extremidade do arco de medida (alfa)", em relação ao eixo x.
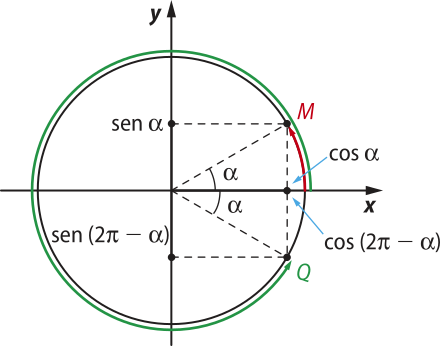
Pela simetria, os pontos M e Q têm ordenadas opostas, porém mesma abscissa.
Logo:
sen (2(pi)" − (alfa)") = −sen (alfa)"
cos (2(pi)" − (alfa)") = cos (alfa)"
Pense e responda
dêz-creva como determinar o seno e o cosseno de arcos quê estão fora da primeira volta da circunferência trigonométrica, como .
Espera-se quê os estudantes respondam quê é necessário obtêr a 1ª determinação positiva do arco, pois o seno e o cosseno do arco fora da primeira volta terão o mesmo valor quê o seno e o cosseno da 1ª determinação positiva. No caso, a 1ª determinação positiva de é igual a + 1 ⋅ 2(pi)".
Para acessar
• FERREIRA, Fábio M. Pontos simétricos na circunferência trigonométrica. [S. l.]: GeoGebra, c2024. Disponível em: https://livro.pw/enzqi. Acesso em: 2 out. 2024.
Esse línki apresenta um applet do software GeoGebra em quê é possível visualizar as simetrias na circunferência trigonométrica, variando a posição do ponto quê representa um arco da circunferência.
Página cento e sessenta e cinco
Relação fundamental da Trigonometria
No estudo das razões trigonométricas no triângulo retângulo, você estudou a relação fundamental da Trigonometria. Agora, vamos verificar quê essa relação é válida para qualquer arco.
Considere, na circunferência trigonométrica, o arco de medida (alfa)", como mostra a figura.
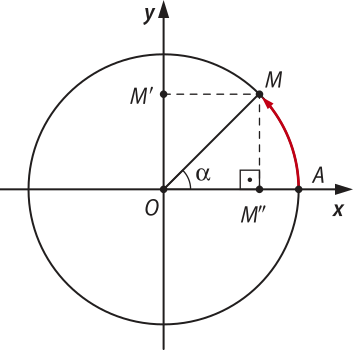
Os pontos M(minutos)" e M(segundos)" são as projeções ortogonais do ponto M sobre os eixos y e x, respectivamente. No triângulo retângulo OM(segundos)"M, pelo teorema de Pitágoras, temos:
(MM(segundos)")2 + (OM(segundos)")2 = (OM)2
Para M no primeiro quadrante, os valores do seno e do cosseno de (alfa)" são positivos. Então, OM(segundos)" = cos (alfa)" e OM(minutos)" = MM(segundos)" = sen (alfa)". Além díssu, OM = 1. Assim:
(MM(segundos)")2 + (OM(segundos)")2 = (OM)2 ⇒ (sen (alfa)")2 + (cos (alfa)")2 = 12
Ou, ainda:
sen2 (alfa)" + cos2 (alfa)" = 1
Pense e responda
por quê podemos afirmar quê OM = 1?
Porque o segmento é o raio da circunferência trigonométrica, quê, por definição, méde 1.
Essa relação, denominada relação fundamental da Trigonometria, é válida para todos os valores de (alfa)", inclusive para aqueles em quê o ponto M pertence a um dos eixos. Observe.
• Segundo quadrante
sen (180° − (alfa)") = sen (alfa)" ⇒ sen2 (180° − (alfa)") = sen2 (alfa)"
cos (180° − (alfa)") = −cos (alfa)" ⇒ cos2 (180° − (alfa)") = (−cos (alfa)")2 = cos2 (alfa)"
Então, temos quê: sen2 (180° − (alfa)") + cos2 (180° − (alfa)") = sen2 (alfa)" + cos2 (alfa)" = 1
• Terceiro quadrante
sen (180° + (alfa)") = −sen (alfa)" ⇒ sen2 (180° + (alfa)") = (−sen (alfa)")2 = sen2 (alfa)"
cos (180° + (alfa)") = −cos (alfa)" ⇒ cos2 (180° + (alfa)") = (−cos (alfa)")2 = cos2 (alfa)"
Então, temos quê: sen2 (180° + (alfa)") + cos2 (180° + (alfa)") = sen2 (alfa)" + cos2 (alfa)" = 1
• Quarto quadrante
sen (360° − (alfa)") = −sen (alfa)" ⇒ sen2 (360° − (alfa)") = (−sen (alfa)")2 = sen2 (alfa)"
cos (360° − (alfa)") = cos (alfa)" ⇒ cos2 (360° − (alfa)") = cos2 (alfa)"
Então, temos quê: sen2 (360° − (alfa)") + cos2 (360° − (alfa)") = sen2 (alfa)" + cos2 (alfa)" = 1
• M pertencente aos eixos
Para 0° ou 360°: sen2 360° + cos2 360° = 02 + 12 = 1
Para 90°: sen2 90° + cos2 90° = 12 + 02 = 1
Para 180°: sen2 180° + cos2 180° = 02 + (−1)2 = 1
Para 270°: sen2 270° + cos2 270° = (−1)2 + 02 = 1
Assim, verificamos quê a relação fundamental da Trigonometria vale para arcos em qualquer quadrante ou com extremidade nos eixos.
Página cento e sessenta e seis
ATIVIDADES RESOLVIDAS
6. Calcule o valor de cos 13(pi)".
Resolução
Como o arco de medida 13(pi)" não está na primeira volta, devemos estabelecer a 1ª determinação positiva dele, assim:
13(pi)" = (pi)" + 12(pi)" = (pi)" + 6 ⋅ 2(pi)"
Então, 13(pi)" é côngruo a (pi)", portanto cos 13(pi)" = cos (pi)".
Como cos (pi)" = −1, então cos 13(pi)" = −1.
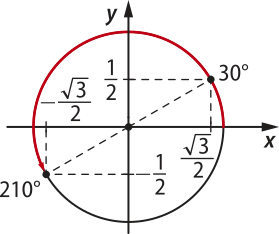
7. Calcule os valores de sen 210° e de cos 210°.
Resolução
O arco de 210° está no terceiro quadrante. Além díssu, observamos quê 210° = 180° + 30°. Assim, temos:
Então, podemos concluir quê:
sen 210° = −sen 30° =
cos 210° = −cos 30° =
8. Calcule o valor da expressão:
E =
Resolução
Para calcular o valor de E, precisamos determinar cada uma das razões trigonométricas da expressão. Como todos os arcos são maiores do quê uma volta da circunferência trigonométrica, vamos calcular a 1ª determinação positiva de cada um deles:
• 1.830° = 30° + 5 ⋅ 360°
• 14(pi)" = 7 ⋅ 2(pi)" = 0 + 7 ⋅ 2(pi)"
• + 2 ⋅ 2(pi)"
Então, 1.830° é côngruo a 30°, 14(pi)" é côngruo a 0 e é côngruo a . Com base nessas informações, vamos calcular as razões trigonométricas da expressão.
• sen 1.830° = sen 30° =
• cos 14(pi)" = cos 0° = 1
• sen = sen
O arco está no terceiro quadrante e = (pi)" + Assim:
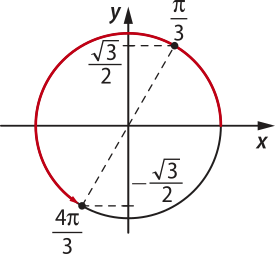
Então: sen = −sen =
Agora quê temos os valores de todas as razões trigonométricas, vamos substituí-las na expressão para determinar o valor de E.
E = =
Portanto, E = .
9. Dado sen (alfa)" = , com 0 < (alfa)" < calcule cos (alfa)".
Resolução
No enunciado, é dado o valor do seno de um ângulo no primeiro quadrante e é pedido o cosseno dêêsse ângulo. A relação fundamental da Trigonometria relaciona o seno e o cosseno de um ângulo, então vamos aplicá-la.
sen2 (alfa)" + cos2 (alfa)" = 1 ⇒ + cos2 (alfa)" = 1
+ cos2 (alfa)" = 1 ⇒ cos2 (alfa)" =
cos (alfa)" = ⇒ cos (alfa)" =
Agora, precisamos determinar se o cosseno é positivo ou negativo. Do enunciado, sabemos quê o ângulo (alfa)" pertence ao primeiro quadrante. Estudamos quê o cosseno nesse quadrante é positivo. Então:
cos (alfa)" =
Página cento e sessenta e sete
10. Para quais valores de m temos, simultaneamente, sen (alfa)" = m + 1 e cos (alfa)" = m?
Resolução
Vamos usar a relação fundamental para substituir os valores de seno e de cosseno e determinar os possíveis valores de (alfa)".
sen2 (alfa)" + cos2 (alfa)" = 1 ⇒ (m + 1)2 + m2 = 1 ⇒ m2 + 2m + 1 + m2 − 1 = 0 ⇒ 2m2 + 2m = 0 ⇒ m(2m + 2) = 0 ⇒ m = 0 ou 2m + 2 = 0 ⇒ m = −1
Portanto, os possíveis valores são m = 0 ou m = −1.
ATIVIDADES
18. Calcule os valores indicados a seguir.
a) sen 150°
b) cos 150°
c) sen 240°
d) cos 240°
e) sen 315° + cos 315°
zero
19. Calcule os valores do seno e do cosseno dos seguintes arcos:
Ver as Orientações para o professor.
a) 135°
b)
c)
d) −240°
20. (hú- hê- érre jota) O círculo a seguir tem o centro na origem do plano cartesiano xy e raio igual a 1. Nele, determina um arco de 120°.
As coordenadas de P são:
a)
b)
c)
d)
alternativa a
21. Encontre o número real expresso por:
a) sen 360° + sen 540° − 4 sen 1.710°
4
b) cos 810° + 4 cos 3.780° cos 1.350°
−4
22. Usando (pi)" ≃ 3,14, verifique se:
a) sen 8 > 0;
verdadeiro
b) cos 10 < 0;
verdadeiro
c) sen 5 > 0.
falso
• ![]() Reúna-se a um colega e explique a ele como você raciocinou para realizar a atividade. Vocês pensaram da mesma maneira?
Reúna-se a um colega e explique a ele como você raciocinou para realizar a atividade. Vocês pensaram da mesma maneira?
Resposta pessoal.
23. Simplifique as expressões a seguir.
a) sen (9(pi)" − (alfa)") + sen (5(pi)" − (alfa)")
2sen (alfa)"
b) sen ((alfa)" − 900°) + cos ((alfa)" − 540°)
−sen (alfa)" − cos (alfa)"
c) sen (4(pi)" − (alfa)") + cos (8(pi)" − (alfa)") − sen (720° − (alfa)")
cos (alfa)"
24. Determine o quadrante em quê está o arco (alfa)" sabendo quê:
a) cos (alfa)" > 0 e sen (alfa)" > 0
primeiro quadrante
b) sen (alfa)" > 0 e cos (alfa)" < 0
segundo quadrante
25. Represente, na circunferência trigonométrica, um ângulo (alfa)" tal quê:
Ver as Orientações para o professor.
a) sen (alfa)" =
b) sen (alfa)" =
c) sen (alfa)" = com (alfa)" ∈
26. Sabendo quê (alfa)" = , calcule:
A = sen − 3 sen 2(alfa)" +
A =
27. Calcule o valor da expressão:
2sen (pi)" ⋅ sen ((pi)" − (alfa)") ⋅ sen para (alfa)" =
zero
Página cento e sessenta e oito
28. Calcule o valor da expressão:
sen 8(pi)" + sen − sen
29. Relacione os senos e cossenos da coluna da esquerda com os seus respectivos valores na coluna da direita.
Alguns valores serão relacionados com mais de uma razão trigonométrica.
a) sen 120°
b) sen 150°
c) cos 120°
d) cos 150°
e) sen
f) sen
g) cos
h) cos
I.
II.
III.
IV.
a-I; b-II; c-IV; d-III; e-IV; f-II; g-I; h-III
30. (PUC-SP) Sendo cos x = e sen x = , determine m.
2 ou −1
31. (Fuvest-SP) Qual dos números é maior? Justifique.
a) sen 830° ou sen 1.195°
sen 830°
b) cos (−535°) ou cos 190°
cos 190°
32. (FEI-SP) Calcular sen ⋅ cos (31(pi)").
1
33. Se k ∈ ℕ e k < 4, quanto vale a soma dos números da forma cos (k ⋅ )?
zero
34. Sendo sen (alfa)" = e cos (alfa)" = a − 1, determine a.
a = 2
35. (UFMS) Calcule todos os valores reais de (alfa)", para os quais valem, simultaneamente, as igualdades sen x = a + e cos x = a , sêndo x um número real.
a =
36. Adotando sen 25° = 0,42 e cos 25° = 0,91, calcule:
a) sen 205° e cos 205°
−0,42; −0,91
b) sen (−25°) e cos (−25°)
−0,42; 0,91
c) sen 335° e cos 335°
−0,42; 0,91
37. Você já ouviu falar no Sangaku?
Sangaku são gravuras em madeira quê foram escritas em uma língua antiga do Japão durante o período Edo (1603-1868). Elas continham teoremas geométricos e normalmente eram entregues como oferendas em templos xintoístas em agradecimento por bons desempenhos escolares.
• Acompanhe um exemplo de problema encontrado em um Sangaku datado de 1879.
[...] um anel de oito pequenos círculos de raio t, cujos centros se encontram nos vértices de um octógono regular, é circunscrito por um círculo de raio R e circunscreve um círculo de raio r. Encontre R e r em termos de t.
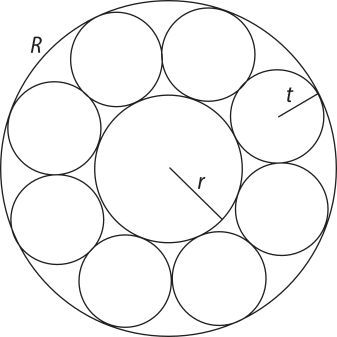
SANTOS, Thaynara K. O. Sangaku: a matemática sagrada. 2018. Trabalho de Conclusão de Curso (Licenciatura em Matemática) – Instituto Federal de Educação Ciência e Tecnologia de São Paulo, São Paulo, 2018. p. 46. Disponível em: https://livro.pw/pcnus. Acesso em: 12 set. 2024.
![]() Agora, reúna-se a um colega e façam o quê se pede em cada item a seguir.
Agora, reúna-se a um colega e façam o quê se pede em cada item a seguir.
Ver as Orientações para o professor.
a) Vocês já tí-nhão ouvido falar a respeito do Sangaku? Pesquisem sobre ele, suas origens, problemas escritos nele e informações quê tênham curiosidade em saber.
b) Resolvam o problema do Sangaku apresentado. Dado: sen 22,5° ≃ 0,38.
c) Agora é a vez de vocês! Criem um painel inspirado no Sangaku: pensem em um problema geométrico quê envolva os conteúdos vistos até agora e o representem em uma fô-lha de papel. Depois, tróquem o Sangaku criado com outra dupla, para quê uma resôuva o problema elaborado pela outra.
Resposta pessoal.
Página cento e sessenta e nove
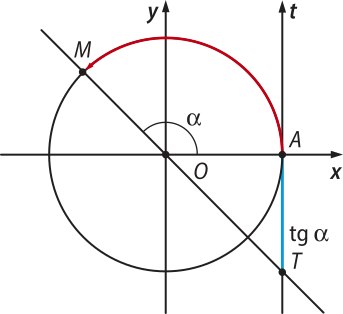
Tangente de um arco
Já analisamos o comportamento das razões seno e cosseno na circunferência trigonométrica. Agora, vamos estudar o comportamento da tangente.
Seja M um ponto da circunferência trigonométrica associado ao número real (alfa)". Isto é, M é a extremidade final do arco de medida (alfa)" radianos.
Tomemos o eixo t, paralelo ao eixo dos senos, orientado no mesmo sentido e tangente à circunferência no ponto A. O eixo t é chamado de eixo das tangentes, e o ponto A é a origem do eixo das tangentes.
Seja T o ponto de intersecção da reta com o eixo t das tangentes. Define-se:
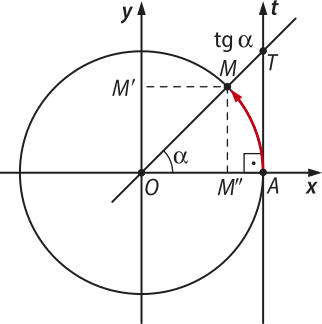
A tangente de (alfa)" é a ordenada do ponto T.
Verificamos quê:
• essa definição preserva a relação entre tangente, seno e cosseno para qualquer ângulo (alfa)", em quê cos (alfa)" ≠ 0. Por exemplo, no primeiro quadrante, nos triângulos OM(segundos)"M e OAT da figura anterior, temos:
(triângulo)"OM(segundos)"M ∼ (triângulo)"OAT ⇒ ⇒ ⇒ cos (alfa)" ⋅ tg (alfa)" = 1 ⋅ sen (alfa)" ⇒ tg (alfa)" = com cos (alfa)" ≠ 0
• quando a reta coincide com o eixo dos cossenos, temos tg (alfa)" = 0.
Observe quê a ordenada de T é 0 quando isso acontece. Assim, tg 0° = 0 e tg (pi)" = 0.
Note quê, nesse caso, vale a relação tg (alfa)" = , pois sen 0° = 0 e sen (pi)" = 0.
• quando a reta coincide com o eixo dos senos, não existe ponto de intersecção T dessa reta com o eixo das tangentes, então não existe tg (alfa)". Assim, tg e tg 270° não estão definidas.
Portanto, a tangente só não está definida para + k(pi)", com k ∈ ℤ.
Como o eixo das tangentes é orientado para cima, a tangente é positiva quando (alfa)" é do primeiro ou do terceiro quadrantes e é negativa quando (alfa)" é do segundo ou do quarto quadrantes, como indicado nas imagens da página a seguir.
Saiba quê...
A tangente de um ângulo também póde sêr indicada como tan. Escrever tg (alfa)" é o mesmo quê escrever tan (alfa)". Essa notação póde sêr encontrada, por exemplo, em algumas calculadoras científicas e programas de computador.
Pense e responda
• Relacione a definição da tangente no triângulo retângulo com a definição da tangente para ângulos na circunferência trigonométrica. Justifique por quê elas coincidem para 0 ≤ (alfa)" <
• por quê podemos afirmar quê (triângulo)"OM(segundos)"M ∼ (triângulo)"OAT?
Ver as Orientações para o professor.
Página cento e setenta
1) No primeiro quadrante, a tangente é positiva.
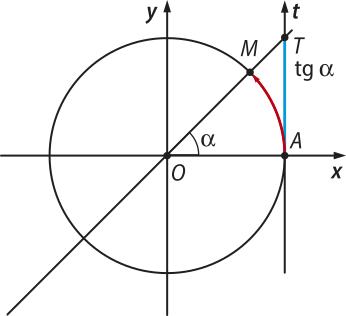
2) No segundo quadrante, a tangente é negativa.
3) No terceiro quadrante, a tangente é positiva.
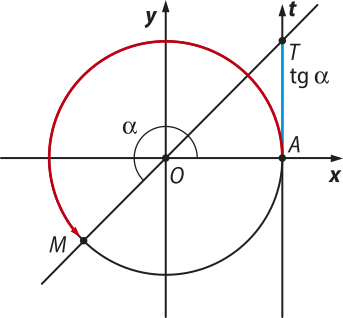
4) No quarto quadrante, a tangente é negativa.
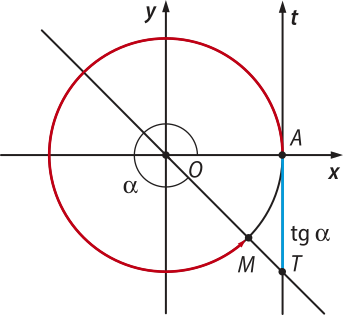
Alguns valores da tangente
Assim como fizemos com o seno e o cosseno, vamos determinar o valor da tangente para alguns arcos mais comuns na circunferência trigonométrica. Para isso, será necessário usar a relação entre as razões tg (alfa)" = e os valores de seno e cosseno dêêsses ângulos vistos anteriormente. Assim:
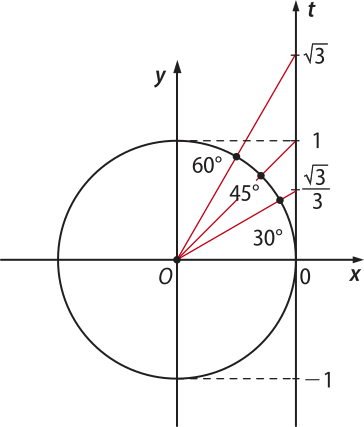
• tg 30° =
• tg 45° = = 1
• tg 60° =
Pense e responda
Há um valor mássimo quê a tangente póde assumir? E um valor mínimo? Se sim, quê valores são esses?
Espera-se quê os estudantes concluam quê não há um valor mássimo nem um valor mínimo, pois a tangente cresce ou diminui indefinidamente.
Logo, podemos escrever:
Medida do arco |
0° ou 0 |
30° ou |
45° ou |
60° ou |
90° ou |
180° ou (pi)" |
270° ou |
360° ou 2(pi)" |
|---|---|---|---|---|---|---|---|---|
tg |
0 |
1 |
não está definida |
0 |
não está definida |
0 |
Página cento e setenta e um
Pense e responda
Reúna-se a um colega e discutam como vocês fariam, apenas com o qüadro apresentado anteriormente e com seus conhecimentos matemáticos, para determinar a tangente do arco de .
Resposta pessoal.
Redução ao primeiro quadrante
Assim como fizemos com o seno e o cosseno, podemos usar as simetrias na circunferência trigonométrica e os valores da tangente no primeiro quadrante para determinar a tangente de arcos nos demais quadrantes. Nesse caso, também estamos fazendo uma redução ao primeiro quadrante.
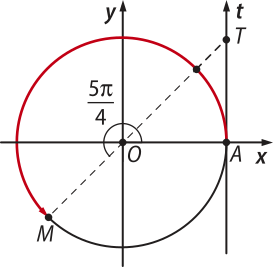
Acompanhe, a seguir, como fazer essa redução ao primeiro quadrante a partir de cada um dos demais quadrantes para (alfa)" ∈ ℝ e (alfa)" ≠ + k(pi)", com k ∈ ℤ.
• Redução do segundo quadrante para o primeiro quadrante
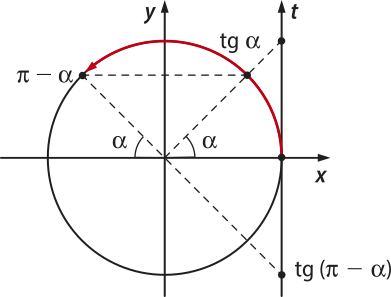
tg ((pi)" − (alfa)") = −tg (alfa)"
• Redução do terceiro quadrante para o primeiro quadrante
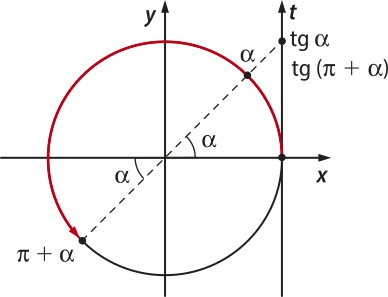
tg ((pi)" + (alfa)") = tg (alfa)"
• Redução do quarto quadrante para o primeiro quadrante
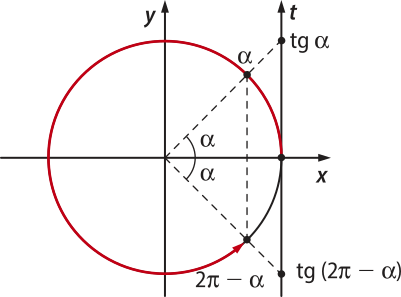
tg (2(pi)" − (alfa)") = −tg (alfa)"
Página cento e setenta e dois
ATIVIDADES RESOLVIDAS
11. Determine o valor de tg 1.845°.
Resolução
O arco de 1.845° é maior do quê uma volta.
Então, vamos calcular a 1ª determinação positiva dele:
1.845° = 45° + 5 ⋅ 360°
Logo, 1.845° é côngruo a 45°. Assim: tg 1.845° = tg 45° = 1
Portanto, tg 1.845° = 1.
12. Sabendo quê cos (alfa)" = e sen (alfa)" > 0, calcule tg − (alfa)".
Resolução
Vamos usar a relação fundamental da Trigonometria para determinar o valor de sen (alfa)".
sen2 (alfa)" + cos2 (alfa)" = 1 ⇒ sen2 (alfa)" + = 1 ⇒ sen2 (alfa)" = 1 − ⇒ sen2 (alfa)" = ⇒ sen (alfa)" =
Do enunciado, sen (alfa)" > 0. Então, sen (alfa)" = .
Temos quê tg (alfa)" = , então:
tg (alfa)" = ⇒ tg (alfa)" =
Portanto, tg (alfa)" = .
ATIVIDADES
38. Calcule o valor de:
a) tg 150°
b) tg (−945°)
−1
c) tg
d) tg 7(pi)"
zero
39. Determine o valor de tg (alfa)", dado quê sen (alfa)" = e cos (alfa)" > 0.
40. Calcule A = sen 3(alfa)" + cos 4(alfa)" − tg 2(alfa)" para (alfa)" = .
zero
41. Calcule o valor de cos 510° + tg .
42. Que número é maior: tg 1 ou tg 7?
tg 1
• ![]() Explique a um colega como você raciocinou para resolver a atividade. Vocês pensaram da mesma maneira?
Explique a um colega como você raciocinou para resolver a atividade. Vocês pensaram da mesma maneira?
Resposta pessoal.
43. Calcule o valor de:
a) tg (alfa)" + tg 3(alfa)" + tg 5(alfa)" para (alfa)" =
1
b) tg (alfa)" + tg 2(alfa)" + tg 4(alfa)" para (alfa)" = −60°
44. Determine m para quê seja raiz da equação:
tg2 (alfa)" − m cos2 (alfa)" + sen2 (alfa)" = 0
m = 15
45. Sendo sen (alfa)" = e (pi)" < (alfa)" < calcule:
a) cos (alfa)"
b) tg (alfa)"
46. (FEI-SP) Sendo (alfa)" um arco com extremidade no terceiro quadrante e sabendo quê cos (alfa)" = então 3sen (alfa)" + 4tg (alfa)" é igual a:
a)
b)
c)
d)
e)
alternativa b
47. Simplifique a expressão − tg2 (alfa)".
2
48. (Fuvest-SP) Se tg x = , com (pi)" < x < , determine o valor de y = cos x − sen x.
49. Qual é o sinal do produto tg 28° ⋅ tg 230° ⋅ tg 307°?
negativo
50. Verifique se tg > sen .
verdadeiro
51. (ITA-SP) Sabendo quê cos θ = e tg θ < 0, calcule o valor da expressão:
x =
Página cento e setenta e três
Trigonometria em um triângulo qualquer
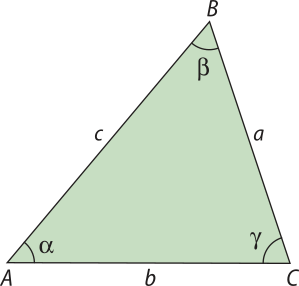
Já estudamos as razões trigonométricas em um triângulo retângulo e na circunferência. Agora, vamos ampliar essa teoria calculando as razões trigonométricas e as medidas de ângulos e lados em um triângulo qualquer. Para isso, serão apresentadas, neste tópico, a lei dos senos e a lei dos cossenos.
Lei dos cossenos
Em algumas situações, podemos modelar um problema por meio de um triângulo qualquer, em quê é necessário calcular uma ou mais medidas dos lados ou dos ângulos. Para realizar esses cálculos, utilizamos a lei dos cossenos, enunciada a seguir.
Em qualquer triângulo, o quadrado da medida de um lado é igual à soma dos quadrados das medidas dos outros dois lados menos o dôbro do produto das medidas dêêsses lados pelo cosseno do ângulo formado por eles.
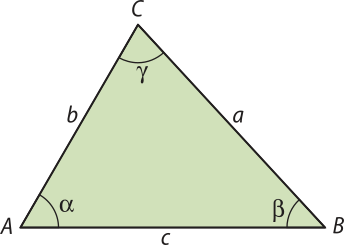
Assim, dado um triângulo ABC qualquer com as medidas dos lados e dos ângulos como indicado na figura a seguir, podemos escrever:
a² = b² + c² − 2 ⋅ b ⋅ c ⋅ cos (alfa)"
b² = a² + c² − 2 ⋅ a ⋅ c ⋅ cos (beta)"
c² = a² + b² − 2 ⋅ a ⋅ b ⋅ cos (gama)"
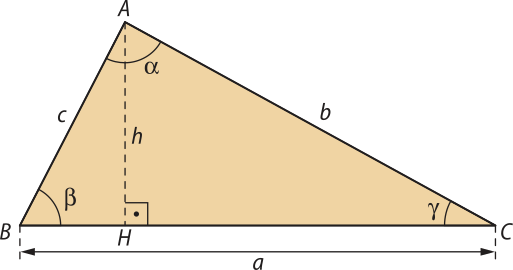
Vamos demonstrar apenas a primeira sentença para o ângulo (alfa)"; as demais são análogas. Para isso, primeiro vamos demonstrar a validade da sentença para os casos em quê (alfa)" é um ângulo agudo ou obtuso e, em seguida, verificar a validade para o ângulo reto como consequência do teorema de Pitágoras. Acompanhe a seguir cada um dêêsses casos.
1º caso: (alfa)" é um ângulo agudo
Considere o triângulo acutângulo ABC, no qual é a altura relativa ao lado , conforme mostra a figura.

No triângulo retângulo BCH, temos: a2 = h2 + (c − m)2 I
No triângulo retângulo ACH, temos:
b2 = h2 + m2 ⇒ h2 = b2 − m2 II
Substituindo II em I, temos:
a2 = b2 − m2 + (c − m)2 ⇒ a2 = b2 + c2 − 2 ⋅ c ⋅ m III
Ainda no triângulo retângulo ACH, temos: cos (alfa)" = ⇒ m = b ⋅ cos (alfa)" IV
Substituindo IV em III, obtemos:
a2 = b2 + c2 − 2 ⋅ c ⋅ (b ⋅ cos (alfa)") ⇒ a2 = b2 + c2 − 2 ⋅ b ⋅ c ⋅ cos (alfa)"
Página cento e setenta e quatro
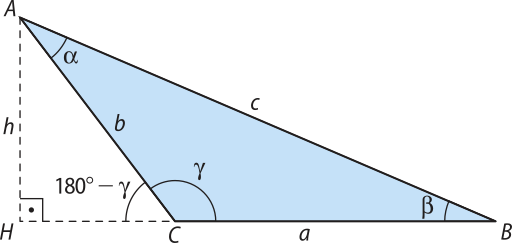
2º caso: (alfa)" é um ângulo obtuso
Considere o triângulo obtusângulo ABC, no qual é a altura relativa ao lado e é o ângulo interno obtuso, conforme mostra a figura.
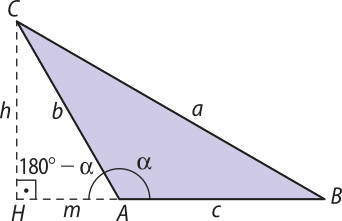
No triângulo retângulo BCH, temos:
a2 = h2 + (c + m)2 I
No triângulo retângulo ACH, temos:
b2 = h2 + m2 ⇒ h2 = b2 − m2 II
Substituindo II em I, temos:
a2 = b2 − m2 + (c + m)2 ⇒ a2 = b2 + c2 + 2 ⋅ c ⋅ m III
Ainda no triângulo retângulo ACH, temos:
cos (180° − (alfa)") =
Como cos (180° − (alfa)") = −cos (alfa)", temos:
−cos (alfa)" = ⇒ m = −b ⋅ cos (alfa)" IV
Substituindo IV em III, obtemos:
a2 = b2 + c2 + 2 ⋅ c ⋅ (−b ⋅ cos (alfa)") ⇒ a2 = b2 + c2 − 2 ⋅ b ⋅ c ⋅ cos (alfa)"
3º caso: (alfa)" é um ângulo reto
Considere um triângulo ABC retângulo em A, conforme mostra a figura.
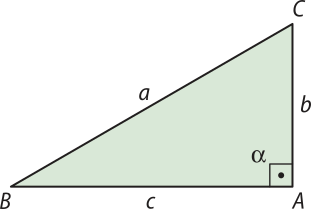
Como (alfa)" é o ângulo reto e cos 90° = 0, temos:
a2 = b2 + c2 − 2 ⋅ b ⋅ c ⋅ cos 90° ⇒ a² = b² + c²
cos 90° ← 0
Note quê, em relação ao ângulo reto, a lei dos cossenos fica reduzida ao teorema de Pitágoras.
ATIVIDADE RESOLVIDA
13. Um engenheiro quer construir um túnel entre os pontos A e B, onde se localiza um morro, conforme o esquema a seguir. Do ponto C, ele visualiza os pontos A e B e obtém os valores
AC = 260 m, BC = 420 m e = 52°.
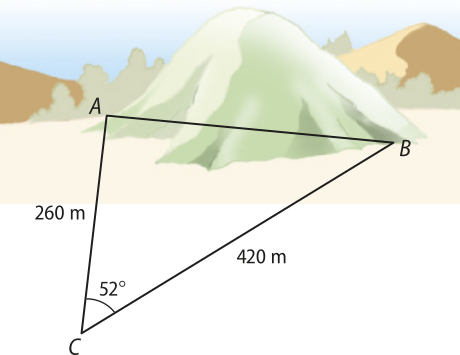
Qual será o comprimento, em métro, dêêsse túnel? (Adote cos 52° = 0,62.)
Resolução
O triângulo a seguir representa a situação.
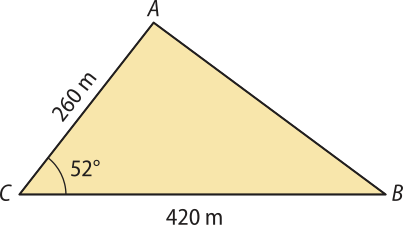
Aplicando a lei dos cossenos:
(AB)2 = (AC)2 + (BC)2 − 2 ⋅ (AC) ⋅ (BC) ⋅ cos 52°
(AB)2 = 2602 + 4202 − 2 ⋅ 260 ⋅ 420 ⋅ 0,62
AB2 = 67.600 + 176.400 − 135.408
AB2 = 108.592 ⇒ AB ≃ 329,53, pois AB > 0
Portanto, o comprimento do túnel será de aproximadamente 329,53 m.
Página cento e setenta e cinco
ATIVIDADES
52. Em um triângulo de vértices A, B e C, a medida do ângulo é igual a 60°. Se AC = 80 m e BC = 100 m, qual é, aproximadamente, em métro, a medida de ?
AB ≃ 91,65 m
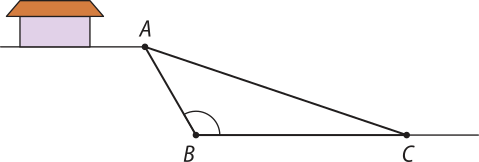
53. (UEPA) A figura a seguir mostra o kórti lateral de um terreno onde será construída uma rampa reta , quê servirá para o acesso de veículos à casa, quê se encontra na parte mais alta do terreno. A distância de A a B é de 6 m, de B a C é de 10 m e o menor ângulo formado entre e é de 120°.
Então, o valor do comprimento da rampa deve sêr de:
alternativa e
a) 12 m.
b) 12,5 m.
c) 13 m.
d) 13,5 m.
e) 14 m.
54. (hú- hê- érre jota) Ao coletar os dados para um estudo topográfico da margem de um lago a partir dos pontos A, B e T, um técnico determinou as medidas ÉTI = 32 m; BT = 13 m e = 120°, representadas no esquema abaixo.
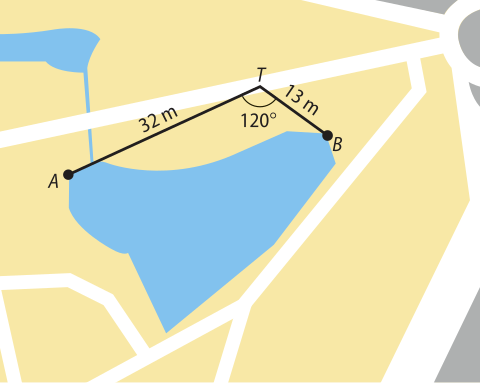
• Calcule a distância aproximada, em métro, entre os pontos A e B, definidos pelo técnico nas margens dêêsse lago.
aproximadamente 40 m
55. Em um paralelogramo, o lado maior méde 7 cm e a diagonal menor méde cm. Verifique se é possível calcular as medidas dos ângulos dêêsse paralelogramo. Em caso afirmativo, quais são essas medidas?
A questão é irresolúvel, pois falta um dado.
56. (Fatec-SP) Na figura a seguir, além das medidas dos ângulos indicados, sabe-se quê B é ponto médio de e AC = 2 cm.
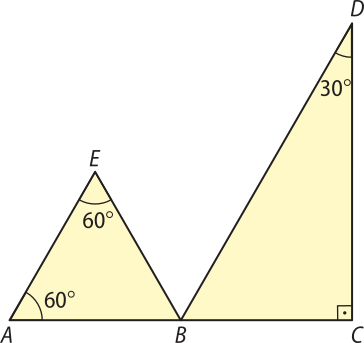
A medida de , em centimetro, é igual a:
a) .
b) 1.
c) .
d) 1,5.
e) .
alternativa e
57. Observe o visor de um relógio de ponteiros quê marca 2 horas.

Sabendo quê os ponteiros menor (das horas) e maior (dos minutos) médem, respectivamente, 50 cm e 80 cm, calcule a distância entre suas extremidades nesse horário.
70 cm
58. Joana é artesã e quer fazer um ornamento com fios coloridos. Ela escolheu uma peça em formato de triângulo, cujas medidas estão indicadas na figura 1, para compor o pingente de um colar. Ela precisa de quatro peças dessas para completar seu artesanato, como póde sêr notado no modelo na figura 2.
Sabendo quê a medida do lado é 5 cm e quê a de é 6 cm, quantos centimetros de fio colorido ela utilizará para fazer o pingente, considerando apenas o comprimento de fio utilizado para fazer os triângulos?


aproximadamente 66,28 cm
Página cento e setenta e seis
Lei dos senos
Outra maneira de calcular as medidas de lados e ângulos de um triângulo qualquer é por meio da lei dos senos, apresentada a seguir.
Em qualquer triângulo, as medidas dos lados são proporcionais aos senos dos respectivos ângulos opostos, e a constante de proporcionalidade é igual à medida do diâmetro da circunferência circunscrita a esse triângulo.
Assim, dado um triângulo ABC qualquer com as medidas dos lados e dos ângulos como indicado na figura, e tal quê a medida do raio da circunferência circunscrita ao triângulo é R, valem as relações:
= 2R
Acompanhe agora a demonstração da lei dos senos. Faremos essa demonstração para o ângulo agudo (alfa)".
Demonstração
O triângulo ABC representado a seguir está inscrito em uma circunferência de centro O e raio R. Nessa figura, traçamos o diâmetro .

Como e são ângulos inscritos, temos:
⇒ φ = (alfa)"
Observe quê o triângulo BCD é retângulo em C, pois o arco tem medida igual a 180°. Logo, o ângulo tem medida igual a 90°. Assim, temos: sen φ = ⇒ sen (alfa)" = ⇒ 2R =
Analogamente, podemos provar quê: 2R = e 2R =
Saiba quê...
• Dizemos quê um polígono é inscrito em uma circunferência se todos os vértices dêêsse polígono forem pontos da circunferência. Nesse caso, podemos dizêr também quê a circunferência é circunscrita ao polígono.
• Um ângulo inscrito na circunferência é aquele cujos lados são secantes à circunferência e cujo vértice é um ponto da circunferência.
• A medida de um ângulo inscrito em uma circunferência é igual à mêtáde da medida do arco da circunferência quê ele determina.
Pense e responda
Se o ângulo (alfa)" for obtuso, temos a seguinte figura:
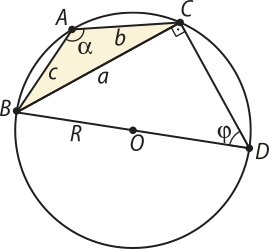
Mostre quê a lei dos senos continua válida.
Ver as Orientações para o professor.
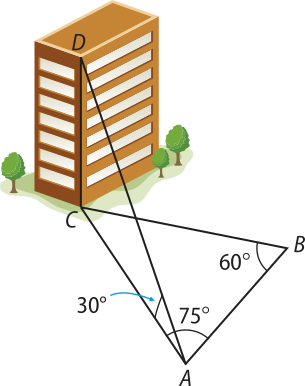
Página cento e setenta e sete
ATIVIDADE RESOLVIDA
14. ![]() Um barco pesqueiro A emite um sinal de socorro, quê é recebido por outros dois barcos, B e C, distantes entre si 70 km. Sabendo quê os ângulos e médem, respectivamente, 64° e 50°, responda: qual dos barcos, B ou C, encontra-se mais próximo do barco pesqueiro? A quê distância ele está do barco A?
Um barco pesqueiro A emite um sinal de socorro, quê é recebido por outros dois barcos, B e C, distantes entre si 70 km. Sabendo quê os ângulos e médem, respectivamente, 64° e 50°, responda: qual dos barcos, B ou C, encontra-se mais próximo do barco pesqueiro? A quê distância ele está do barco A?
Resolução
Representando a situação em um triângulo ABC, temos a seguinte figura.
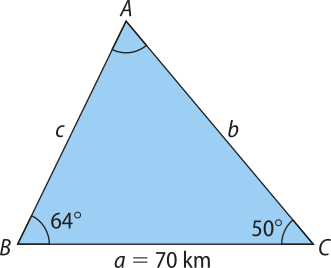
A soma das medidas dos ângulos internos do triângulo ABC é 180°. Logo:
med() + med() + med() = 180°
med() + 64° + 50° = 180°
med() = 66°
Portanto, o ângulo méde 66°.
Aplicando a lei dos senos, obtemos:
Usando uma calculadora científica, obtemos as seguintes aproximações: sen 50° ≃ 0,77, sen 64° ≃ 0,90 e sen 66° ≃ 0,91.
• Calculando a distância entre A e C, temos:
⇒ b ≃ 69,2
• Calculando a distância entre A e B, temos:
⇒ c ≃ 59,2
O barco mais próximo de A é o barco B, quê está a aproximadamente 59,2 km de distância.
ATIVIDADES
59. ![]() De duas torres de vigilância, A e B, distantes 10 km uma da outra, avista-se um foco de incêndio na floresta, conforme os ângulos assinalados na figura.
De duas torres de vigilância, A e B, distantes 10 km uma da outra, avista-se um foco de incêndio na floresta, conforme os ângulos assinalados na figura.
Qual é a distância aproximada de cada uma das torres até o foco do incêndio?
Utilize uma calculadora científica.
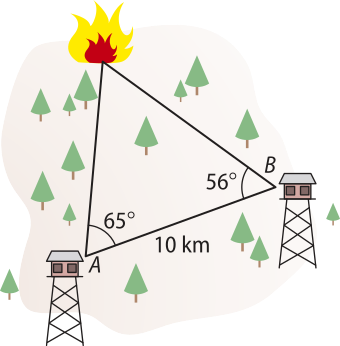
torre A: ≃9,67 km e torre B: ≃10,57 km
60. No triângulo ABC, AC = 4 m, BC = 3 m e (beta)" = 60°. Calcule sen (alfa)".
sen (alfa)" =
61. ![]() Observe a figura.
Observe a figura.
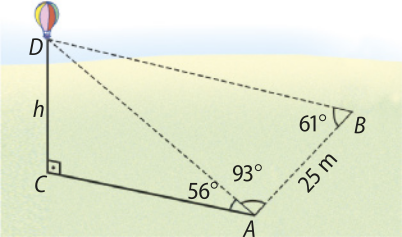
a) Qual é a distância do balão até o ponto A?
aproximadamente 49,43 m
b) A quantos metros de altura o balão está do solo?
aproximadamente 41 m
62. ![]() (Unicamp-SP) Sejam A, B, C e N quatro pontos em um mesmo plano, conforme mostra a figura a seguir.
(Unicamp-SP) Sejam A, B, C e N quatro pontos em um mesmo plano, conforme mostra a figura a seguir.
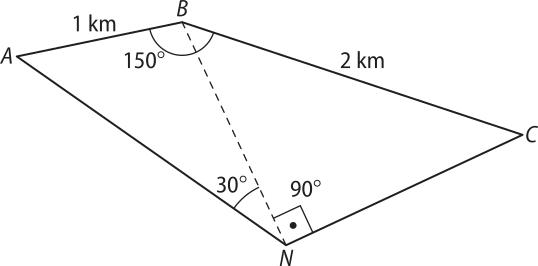
a) Calcule o raio da circunferência quê passa pêlos pontos A, B e N.
1 km
b) Calcule o comprimento do segmento .
km
Página cento e setenta e oito
63. (UnB-DF) Um observador, situado no ponto A, distante 30 m do ponto B, vê um edifício sôbi um ângulo de 30°, conforme a figura. Baseado nos dados da figura, determine a altura do edifício em métro e divída o resultado por .
cê dê = m; 15 m
64. (ITA-SP) Um navio, navegando em linha reta, passa sucessivamente pêlos pontos A, B e C. O comandante, quando o navio está em A, observa um farol L e calcula o ângulo = 30°. Após navegar 4 milhas até B, verifica o ângulo = 75°. Quantas milhas separam o farol do ponto B?
milhas
65. Um triângulo inscrito em uma circunferência de raio igual a 10 cm determina, nesta, três arcos cujos comprimentos são proporcionais aos números 3, 4 e 5. Determine a medida:
a) dos ângulos do triângulo;
45°; 60°; 75°
b) dos lados do triângulo.
10 cm; cm
FÓRUM
Focos de queimadas
Uma área de mais de 17,3 milhões de hectares foi queimada no Brasil em 2023, tamãnho maior quê o território de alguns estados, como Ácri ou Ceará. Houve aumento de 6% em relação a 2022, quando 16,3 milhões de hectares foram atingidos pelo fogo. Os dados são da platafórma Monitor do Fogo, do MapBiomas.
A área total queimada no ano passado [2023] corresponde a aproximadamente 2% do território brasileiro. O pico das queimadas aconteceu nos meses de setembro e outubro, atingindo 4 milhões de hectares.
[...]
BOEHM, Camila. Mais de 17,3 milhões de hectares foram queimados em 2023 no país. Agência Brasil, São Paulo, 19 jan. 2024. Disponível em: https://livro.pw/lihdm. Acesso em: 2 out. 2024.

Há quêimadas que ocorrem como fenômeno natural, especialmente em regiões com clima seco e kemte; no entanto, segundo a coordenadora do MapBiomas Fogo, Ane Alencar, a maioria das queimadas é provocada por atividades humanas deliberadas, como a limpeza de áreas para agricultura, pecuária e expansão urbana. Essas práticas contribuem significativamente para o aumento das áreas queimadas, intensificando os impactos negativos delas sobre o meio ambiente, a economia e a saúde pública.
![]() Diante do cenário alarmante apresentado sobre o aumento das áreas atingidas por queimadas, discuta com os côlégas e o professor a questão a seguir.
Diante do cenário alarmante apresentado sobre o aumento das áreas atingidas por queimadas, discuta com os côlégas e o professor a questão a seguir.
• Como podemos transformar a conscientização sobre os impactos das quêimadas em ações concretas que promovam a preservação ambiental e a sustentabilidade?
Ver as Orientações para o professor.
Página cento e setenta e nove
Área de um triângulo qualquer
Você já estudou no Ensino Fundamental quê a área de um triângulo é calculada pela mêtáde do produto da medida de um lado pela altura relativa a esse lado. Mas, se não se conhece a altura, e sim a medida de dois lados de um triângulo qualquer e o ângulo formado por esses lados, podemos calcular a área dêêsse triângulo utilizando o conceito de seno de um ângulo. Assim, vamos enunciar o seguinte teorema:
A área de um triângulo qualquer é igual à mêtáde do produto das medidas de dois de seus lados pelo seno do ângulo formado por esses lados.
Assim, dado um triângulo ABC qualquer com as medidas de dois lados e a medida do ângulo formado por esses lados como indicado na figura a seguir, sêndo S a área do triângulo ABC, valem as seguintes relações:
S =
S =
S =
Vamos demonstrar esse teorema para o ângulo (gama)", no caso em quê (gama)" é agudo e no caso em quê é obtuso.
Demonstração
Considere o triângulo acutângulo ABC, no qual é a altura relativa ao lado e (gama)" é um ângulo agudo, conforme mostra a figura a seguir.
A área S do triângulo é: S = I
Do triângulo retângulo AHC, temos:
sen (gama)" = ⇒ h = b ⋅ sen (gama)" II
Substituindo II em I, obtemos: S =
Página cento e oitenta
Agora, considere o triângulo obtusângulo ABC, no qual é a altura relativa ao lado e (gama)" é um ângulo obtuso, conforme mostra a figura a seguir.
Sabemos quê a área S é dada por: S = I
Do triângulo retângulo AHC, temos:
sen (180° − (gama)") = sen (gama)" = ⇒ h = b ⋅ sen (gama)" II
Substituindo II em I, temos: S =
Analogamente, podemos mostrar quê:
S = e S =
ATIVIDADE RESOLVIDA
15. ![]() Para obtêr a área de um terreno irregular, um engenheiro dividiu esse terreno em quatro regiões triangulares, formadas a partir de um mesmo vértice, como mostra a figura.
Para obtêr a área de um terreno irregular, um engenheiro dividiu esse terreno em quatro regiões triangulares, formadas a partir de um mesmo vértice, como mostra a figura.
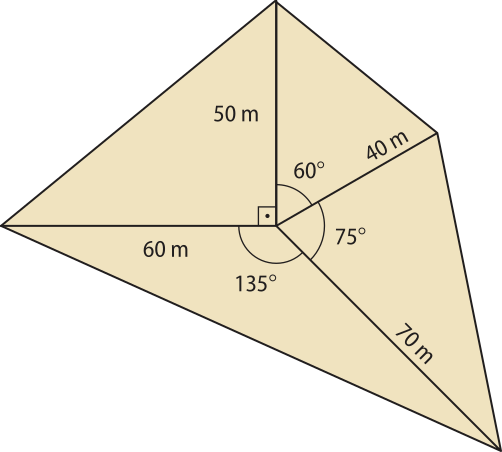
Qual é a área aproximada dêêsse terreno? (Use as aproximações até centésimos.)
Resolução
Em cada um dos triângulos obtidos, temos as medidas de dois lados e do ângulo compreendido entre eles.
Assim, podemos calcular a área de cada triângulo e depois adicioná-las para obtêr a área total. Para isso, com uma calculadora científica, vamos determinar o seno de 75°.
Para os outros ângulos, podemos utilizar os valores já apresentados anteriormente.
• Área do triângulo 1:
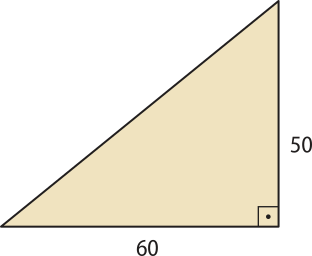
A1 = = 1.500
• Área do triângulo 2:
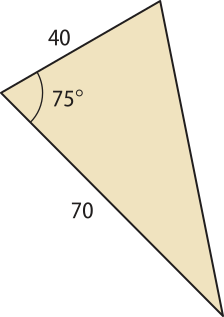
A2 = ≃ 1.400 ⋅ 0,96
A2 ≃ 1.344
Página cento e oitenta e um
• Área do triângulo 3:
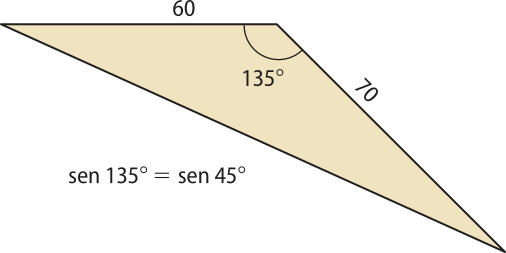
A3 =
A3 = 1.050 ⋅ ≃ 1.050 ⋅ 1,41
A3 ≃ 1.480,50
• Área do triângulo 4:
A4 = = 1.000 ⋅ ≃ 500 ⋅ 1,73
A4 ≃ 865
Então, a área total (At)do terreno é:
At = A1 + A2 + A3 + A4
At ≃ 1.500 + 1.344 + 1.480,50 + 865 = 5.189,50
Portanto, o terreno tem aproximadamente 5.189,50 m2 de área.
ATIVIDADES
66. (IFMA) Preocupado com a falta de área vêrde em sua cidade, um governante rêzouvêo aproveitar cérto terreno triangular, localizado no cruzamento de duas ruas, para construir uma praça arborizada, conforme a figura abaixo:
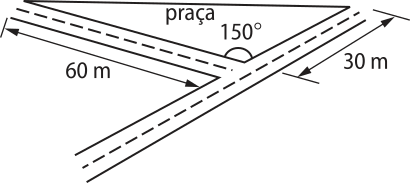
A área da praça a sêr construída, em m2, é:
a) .
b) .
c) .
d) 250.
e) 450.
alternativa e
67. Qual é a área de um triângulo isósceles no qual cada lado congruente méde 10 cm e o ângulo adjacente à base méde 75°?
25 cm2
68. O terreno ABCDE representado pela figura a seguir foi vendido a R$ 35,00 o métro quadrado. Qual é o seu valor? (Use sen 60° ≃ 0,86.)
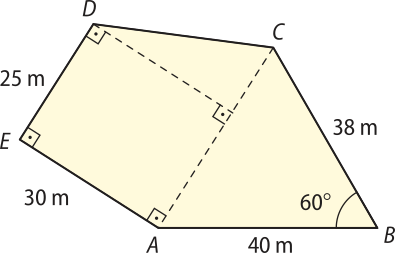
aproximadamente R$ 56.476,00
69. Qual é a área de um paralelogramo no qual dois lados consecutivos médem 7 cm e 5 cm, sabendo quê eles formam um ângulo de 120°?
69. cm2
70. A área do triângulo ABC representado a seguir é cm2.
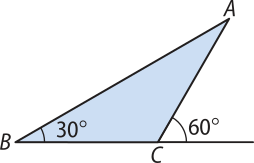
Admitindo quê ≃ 1,7, calcule o perímetro do triângulo ABC.
aproximadamente 37 cm
71. O hekzágono regular cuja medida do lado é x cm2 é formado por seis triângulos equiláteros.
Calcule a área dêêsse hekzágono.
cm2
72. ![]() Elabore um problema cuja resolução envolva aplicar a lei dos cossenos e outro quê envolva calcular a área de um triângulo usando as medidas de dois lados e o seno do ângulo formado por esses lados. Troque os problemas quê você elaborou com um colega e resolvam os problemas um do outro.
Elabore um problema cuja resolução envolva aplicar a lei dos cossenos e outro quê envolva calcular a área de um triângulo usando as medidas de dois lados e o seno do ângulo formado por esses lados. Troque os problemas quê você elaborou com um colega e resolvam os problemas um do outro.
Resposta pessoal.
Página cento e oitenta e dois
CONEXÕES com...
CIÊNCIAS DA NATUREZA E SUAS TECNOLOGIAS e LINGUAGENS E SUAS TECNOLOGIAS
Ciclismo
Você já andou de bicicleta? Se sim, gosta de praticar essa atividade? A bicicleta póde servir de instrumento de lazer para muitas pessoas. Para outras, é um meio de transporte. Há, ainda, pessoas para quem ela é trabalho.
Os atletas profissionais são uma das categorias quê utilizam a bicicleta como ferramenta de trabalho e, nesse caso, dependendo da modalidade praticada, as bicicletas possuem características específicas. Nos Jogos Olímpicos, são disputadas quatro modalidades de ciclismo: mountain báike, ciclismo de estrada, ciclismo de pista e ciclismo bicycle motocross (BMX). Vamos conhecer um pouco de cada uma delas.
Mountain Bike
[...]
Existem dois eventos de mountain báike: um para mulheres e outro para homens. Os ciclistas partem da mesma linha de largada e disputam várias voltas do circuito em um terreno montanhoso e acidentado, quê testa sua técnica, resistência e energia.
As corridas possuem uma largada em massa e, em geral, várias voltas. Os ciclistas levam de uma a duas horas para completar o percurso cheio de reviravoltas e curvas, percorrendo dezenas de quilômetros durante a próva.
[...]
O mountain báike fez sua estreia Olímpica 100 anos depois do ciclismo de pista e do ciclismo de estrada durante os Jogos Olímpicos Atlanta 1996, com provas individuais masculinas e femininas. [...]
COMITÊ OLÍMPICO INTERNACIONAL. Ciclismo mountain báike. [S. l.]: Olympics.com, c2024. Localizável em: Jogos Olímpicos Paris 2024. Disponível em: https://livro.pw/tdgax. Acesso em: 3 out. 2024.


Página cento e oitenta e três
Estrada
[...]
O ciclismo de estrada acontece ao ar livre e é dividido em dois tipos de eventos nos Jogos Olímpicos: a próva de resistência e o contrarrelógio individual.
A corrida de resistência, na qual todos os ciclistas partem ao mesmo tempo em uma largada em massa, é uma proeza altamente tática de esfôrço físico. A corrida (mais de 120 km e de 200 km para mulheres e homens, respectivamente) é freqüentemente vencida em um sprint de algumas centenas de metros, o quê significa quê os ciclistas precisam se posicionar perfeitamente e conservar energia na primeira parte da próva.
O contrarrelógio é um esfôrço individual em quê os competidores partem em tempos escalonados em vez de um pelotão agrupado. [...] o contrarrelógio raramente ultrapassa 50 km. Os eventos exigem consistência, concentração e preservação por meio de um posicionamento aerodinâmico eficaz e poderoso.
[...]
O ciclismo de estrada é um dos eventos Olímpicos originais porque foi incluído no programa competitivo da primeira edição dos Jogos Olímpicos modernos em 1896, em Atenas. [...]
[...]
COMITÊ OLÍMPICO INTERNACIONAL. Ciclismo de estrada. [S. l.]: Olympics.com, c2024. Localizável em: Jogos Olímpicos Paris 2024. Disponível em: https://livro.pw/vixtr. Acesso em: 3 out. 2024.

- Sprint
- : é uma técnica de explosão quê usa a maior velocidade possível quê um ciclista consegue atingir, muitas vezes utilizada no momento final de uma próva.
Pista
[...]
O ciclismo de pista é disputado em uma arena de 250 m no formato de uma tigéla e conhecida como velódromo, com eventos em diferentes formatos de corridas individuais e em equipes. As bicicletas da modalidade são diferentes das utilizadas no ciclismo de estrada por serem fixas e não terem freios.
Acontecem vários tipos de provas na pista, cada uma delas com regras e técnicas específicas. Algumas confiam mais na tática, enquanto outras favorécem a fôrça e potência. [...]
[...]
Uma modalidade Olímpica de longa data, o ciclismo de pista apareceu em todas as edições dos Jogos Olímpicos modernos, com exceção da edição de 1912 em Estocolmo. As mulheres competiram pela primeira vez nestes eventos nos Jogos Olímpicos Seul 1988.
[...]
COMITÊ OLÍMPICO INTERNACIONAL. Ciclismo de pista. [S. l.]: Olympics.com, c2024. Localizável em: Jogos Olímpicos Paris 2024. Disponível em: https://livro.pw/vbkdr. Acesso em: 3 out. 2024.

Página cento e oitenta e quatro
BMX
[…]
BMX é a abreviação de “bicycle motocross”. Refere-se a um tipo de corrida realizada em térra e com saltos, como uma corrida de motocross. Mas, no BMX, a bicicleta não tem motor: são utilizadas bicicletas com rodas pequenas e sem marchas. Segundo o regulamento da União de Ciclismo International (UCI), o órgão internacional de ciclismo quê rege o esporte, as bicicletas de BMX devem ter pedais planos e rodas quê não excedam 22,5 polegadas (57 cm) de diâmetro quando os p-neus estiverem cheios.
Nas competições de BMX Freestyle, as mesmas bicicletas são usadas, mas não para corridas. Em vez díssu, é uma competição julgada com base nas manobras executadas pêlos atletas. Nos Jogos Olímpicos, as competições de BMX Freestyle são realizadas em um “parque”, onde são montados rampas, saltos, corrimãos e degraus para os pilotos saltarem, girarem, darem cambalhotas e voarem.
[…]
O BMX Freestyle estreou nos Jogos Olímpicos de Tóquio 2020. […]
[…]
PRESTO, Greg. BMX freestyle na Olympic Qualifier Series: tudo o quê você precisa saber. [S. l.]: Olympics.com, 23 abr. 2024. Localizável em: Notícias: Jogos Olímpicos Paris 2024. Disponível em: https://livro.pw/krfxo. Acesso em: 3 out. 2024.

[…]
O BMX Racing é um formato muito mais explosivo do quê outras modalidades mais tradicionais do ciclismo, quê tendem a recompensar a resistência ao longo de vários minutos. Já o BMX Racing requer uma intensa explosão de energia por um breve período de alguns segundos. As corridas [...] são disputadas por, no mássimo, oito pilotos em uma pista repleta de saltos, curvas inclinadas e obstáculos, vencendo aquele quê tiver as reações mais ágeis e o ritmo mais rápido.
[…]
Em 2003, o Comitê Olímpico Internacional fez do BMX Racing um esporte Olímpico a partir dos Jogos de Beijing 2008. […]
COMITÊ OLÍMPICO INTERNACIONAL. Ciclismo BMX racing. [S. l.]: Olympics.com, c2024. Localizável em: Jogos Olímpicos Paris 2024. Disponível em: https://livro.pw/wzgms. Acesso em: 3 out. 2024.
Página cento e oitenta e cinco
![]() Agora, reúna-se a um colega, e façam o quê se pede nas atividades a seguir.
Agora, reúna-se a um colega, e façam o quê se pede nas atividades a seguir.
1. Vocês já conheciam essas modalidades de ciclismo? Qual delas mais despertou o interêsse de vocês? No município onde vocês moram, há espaços para a prática de alguma dessas modalidades? Pesquisem a respeito do assunto.
Respostas pessoais.
2. As características das bicicletas diferem de acôr-do com as necessidades de cada modalidade de ciclismo. Por exemplo, o pneu de uma bicicleta de mountain báike tem ranhuras e é mais largo do quê o pneu de uma bicicleta de pista. ob-sérvim as imagens.


Pesquisem como essas diferenças no pneu influenciam a velocidade e a aderência da bicicleta ao solo. Que outros elemêntos da bicicleta influenciam o dêsempênho dela? Elaborem um cartaz com fotos de bicicletas de cada modalidade e dos p-neus usados em cada uma e façam uma comparação entre eles. Apresentem as características de cada tipo de pneu, como medidas de aro, largura, textura, entre outras.
Pesquisa dos estudantes.
3. Vocês sabem como medir o aro da bicicleta? Pesquisem como fazer essa medição e elaborem um texto explicando o quê significa dizêr quê uma bicicleta tem aro 26. Qual é a medida aproximada do perímetro externo, em centimetro, do pneu de uma bicicleta com esse aro?
Pesquisa dos estudantes. O perímetro é aproximadamente 207,4 cm.
4. ![]() Para um praticante de BMX executar determinada manobra com sua bicicleta, ele precisa de uma rampa com a vista lateral como a da figura a seguir.
Para um praticante de BMX executar determinada manobra com sua bicicleta, ele precisa de uma rampa com a vista lateral como a da figura a seguir.
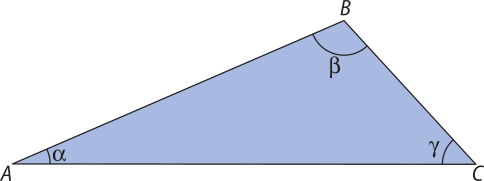
Em seus cálculos, ele determinou quê (alfa)" deve medir 23°, (beta)" deve medir 110° e AB = 2 m. Dessa maneira, quais devem sêr as medidas aproximadas de e de ?
(Usem sen 23° = 0,39, sen 47° = 0,73 e sen 110° = 0,94.)
BC ≃ 1,1 m; AC ≃ 2,6 m
Pense e responda
Que conceitos matemáticos você e seu colega utilizaram para realizar as atividades desta seção?
Resposta esperada: Comprimento da circunferência e lei dos senos.
Para assistir
• DICAS para escolher a bicicleta ideal. [S. l.: s. n.], 2019. 1 vídeo (4 min). Publicado pelo canal Sesc Santa Catarina. Disponível em: https://livro.pw/uugcv. Acesso em: 3 out. 2024.
Nesse vídeo, você vai obtêr algumas recomendações sobre o tipo de bicicleta ideal para você e para o tipo de uso quê você fará dela.
Página cento e oitenta e seis
EXPLORANDO A TECNOLOGIA
Construção de uma calculadora trigonométrica
Estudamos as razões trigonométricas seno, cosseno e tangente na circunferência trigonométrica e conhecemos alguns valores notáveis para essas razões. Também estudamos como determinar essas razões de arcos do segundo, terceiro e quarto quadrantes da circunferência trigonométrica fazendo a redução ao primeiro quadrante. No entanto, póde havêer situações do cotidiano em quê seja necessário calcular as razões trigonométricas para outros arcos ou ângulos, inclusive para valores não inteiros, como 122,3°. Como proceder nesses casos? pôdêmos utilizar diversos recursos, entre eles, uma calculadora científica, um software de Matemática dinâmica ou uma planilha eletrônica, a qual escolhemos para usar neste momento.
Vamos utilizar uma planilha eletrônica para criar nossa própria calculadora trigonométrica, ou seja, uma planilha quê calcula automaticamente os valores das razões trigonométricas para qualquer medida de ângulo.
Para isso, acompanhe a sequência de passos a seguir.
I. Abra uma planilha no Libre Office e salve-a como "CALCTRIGONOMETRICA".
II. Na planilha, para identificar cada uma das razões trigonométricas, digite cada palavra em uma célula, conforme indicado:
• na célula A2: "Ângulo (em grau)";
• na célula A4: "Ângulo (em radiano)";
• na célula C2: "Seno";
• na célula D2: "Cosseno";
• na célula E2: "Tangente".
Após esses passos, sua planilha estará semelhante à imagem a seguir.
Em uma planilha eletrônica, o cálculo das razões trigonométricas é feito com ângulos na unidade radiano. Porém, para facilitar nosso trabalho, vamos digitar o ângulo em grau e utilizaremos uma função para quê o programa realize a transformação de unidades.
Página cento e oitenta e sete
III. A função quê vai realizar esse trabalho é "Radianos()" e, como digitaremos o valor do ângulo, em grau, na célula A3, devemos informar ao programa quê é dessa célula quê ele precisa pegar o valor para fazer a conversão de unidades.
Assim, na célula A5, digite "=Radianos(A3)", e o programa nos fornecerá, nessa célula, em radiano, o valor do ângulo digitado na célula A3.
IV. A planilha eletrônica já tem, em seu banco de dados, fórmulas para o cálculo das razões trigonométricas. Para os cálculos quê queremos, as funções são "Sen()","Cos()" e "Tan()".
Então, digite:
• na célula C3: "=Sen(A5)";
• na célula D3: "=Cos(A5)";
• na célula E3: "=Tan(A5)".
V. Agora, basta inserir o valor do ângulo desejado na célula A3 para obtêr os valores das razões trigonométricas. A imagem a seguir mostra o exemplo para o ângulo de 60°.
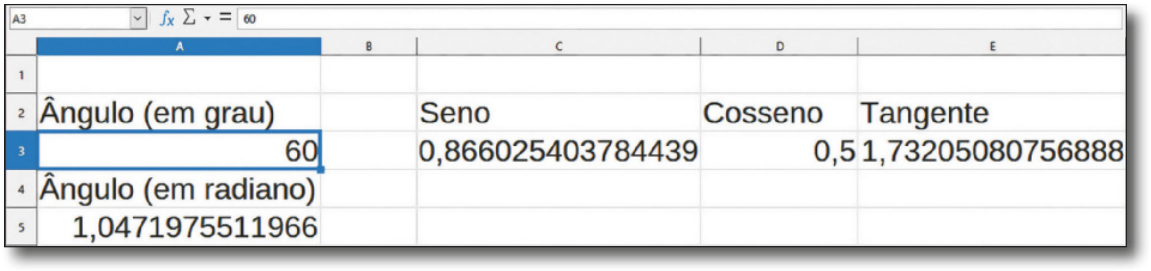
• pôdêmos escolher quantas casas decimais quêremos que a planilha nos mostre. Para alterar a quantidade de casas decimais, primeiro formatamos as células com o recurso Formatar como número, ![]() presente na barra de ferramentas. Para aumentar a quantidade de casas decimais, basta usar a ferramenta
presente na barra de ferramentas. Para aumentar a quantidade de casas decimais, basta usar a ferramenta ![]() e, para diminuir a quantidade de casas decimais, basta usar a ferramenta
e, para diminuir a quantidade de casas decimais, basta usar a ferramenta ![]() .
.
Agora, teste sua calculadora trigonométrica!
Agora, faça o quê se pede nas atividades a seguir.
1. No passo a passo apresentado, optamos por primeiro fazer a conversão da unidade do ângulo, de grau para radiano, para, em seguida, calcular as razões trigonométricas. No entanto, é possível realizar os dois passos de uma vez só. Como podemos fazer isso? Como fica a expressão das funções trigonométricas?
É preciso compor as duas funções para obtêr uma única função. As expressões ficam: "sen(radianos(A3))", "cos(radianos(A3))" e "tan(radianos(A3))".
2. Se, em vez de inserir o ângulo em grau, quiséssemos inserir o valor em radiano, como poderíamos fazer para indicar o valor de (pi)"? Por exemplo, como poderíamos digitar o ângulo de medida para obtêr as razões trigonométricas?
Respostas possíveis: Utilizar um valor aproximado ou utilizar a função pi().
3. ![]() Altere a côr da fonte das células A3 e A5 para branca. Reúna-se a um colega, e cada um de vocês deve digitar um ângulo sem quê o outro veja. O colega terá de adivinhar o quadrante a quê pertence o ângulo digitado observando os sinais das razões trigonométricas obtidas.
Altere a côr da fonte das células A3 e A5 para branca. Reúna-se a um colega, e cada um de vocês deve digitar um ângulo sem quê o outro veja. O colega terá de adivinhar o quadrante a quê pertence o ângulo digitado observando os sinais das razões trigonométricas obtidas.
A resposta depende do ângulo escolhido pêlos estudantes.
Página cento e oitenta e oito
ATIVIDADES COMPLEMENTARES
1. (UFVJM-MG) Esta roleta foi utilizada para realizar um sorteio. Ela foi feita a partir da divisão de uma circunferência em doze partes iguais.

No sorteio essa roleta foi girada saindo do ponto indicado na figura e rodando 780° no sentido horário.
Com base no exposto, o número sorteado foi:
a) 2
b) 3
c) 11
d) 12
alternativa c
2. (Enem/MEC) As cidades de Quito e Singapura encontram-se próximas à linha do equador e em pontos diametralmente opostos no glôbo terrestre. Considerando o raio da Terra igual a 6.370 km, pode-se afirmar quê um avião saindo de Quito, voando em média 800 km/h, descontando as paradas de escala, chega a Singapura em aproximadamente
a) 16 horas.
b) 20 horas.
c) 25 horas.
d) 32 horas.
e) 36 horas.
alternativa c
3. (UEAP) Leia a observação: Sempre escrevemos sen ((pi)") para significar seno de (pi)" radianos. Sobre o valor de y, sêndo y = sen (3) podemos dizêr quê:
a) < y < 1
b) < y <
c) 0 < y <
d) < y < 0
e) < y <
alternativa c
4. (UFVJM-MG) Dada a expressão cos θ = assinale a alternativa quê contém o conjunto de valores quê p póde assumir.
a) −1 ≤ p ≤ 1
b) −1 ≤ p ≤ 2
c) −2 ≤ p ≤ 3
d) −2 ≤ p ≤ 4
alternativa c
5. (UFRRJ) Os valores quê m póde assumir, para quê exista o arco x satisfazendo a igualdade sen x = m − 4, são:
a) m = 2
b) 3 ≤ m ≤ 5
c) 1 ≤ m ≤ 3
d) 0 ≤ m ≤ 2
e) m = 3
alternativa b
6. (Cefet-MG) Os valores de x de modo quê a expressão cos (alfa)" = exista, são:
a) −1 ≤ x ≤ 1
b) −2 ≤ x ≤ 2
c) −1 ≤ x ≤ 2
d) 1 ≤ x ≤ 2
e) −2 ≤ x ≤ −1 ou 1 ≤ x ≤ 2
alternativa b
7. (EsPCEx-SP) Na figura, está representado um círculo trigonométrico em quê os pontos P1 a P5 indicam extremidades de arcos. Esses pontos, unidos, correspondem aos vértices de um pentágono regular inscrito no círculo. Se o ponto P1 corresponde a um arco de radianos, então o ponto P4 corresponderá à extremidade de um arco cuja medida, em radiano, é igual a
a)
b)
c)
d)
e)
alternativa d
Página cento e oitenta e nove
8. (Uneb-BA) Considerando-se sen (alfa)" + cos (alfa)" = , m > 0 e sen (alfa)" ⋅ cos (alfa)" = , pode-se afirmar quê o valor de 2m − n é igual a:
a) 2
b) 1
c) 0
d) −2
e) −3
alternativa a
9. (hú- hê- érre jota) Observe o ângulo central (alfa)" do círculo trigonométrico a seguir:

Admitindo quê 0 ≤ (alfa)" < e cos (alfa)" = , o valor de sen (2(pi)" − (alfa)") é igual a:
a)
b)
c)
d)
alternativa c
10. (Unip-SP) Seja sen (alfa)" = e (alfa)" um arco do segundo quadrante. Então tg (alfa)" vale:
a)
b)
c)
d) −1
e)
alternativa c
11. (UEFS-BA) Sendo x um arco do 2º quadrante, tal quê sen x = , pode-se afirmar quê o valor de A = tg x é igual ao valor de
a) sen
b) cos
c) sen
d) cos
e) sen
alternativa b
12. (UFRR) Indique qual das afirmações abaixo é verdadeira:
a) cos 200° < tg 200° < sen 200°
b) cos 200° < sen 200° < tg 200°
c) sen 200° < tg 200° < cos 200°
d) sen 200° < cos 200° < tg 200°
e) tg 200° < sen 200° < cos 200°
alternativa b
13. (Unicentro-PR) Sendo 270° < x < y < 360°, assinale a alternativa correta.
a) sen x > sen y
b) cos x > cos y
c) tg x > tg y
d) cos y − sen x > 0
e) sen x ⋅ cos y > 0
alternativa d
14. (UEM-PR) Um engenheiro precisa conhecer a medida de cada lado de um terreno triangular cujo perímetro é 20 m, porém a planta do terreno foi rasgada e o quê restou foi um pedaço, como na figura a seguir.
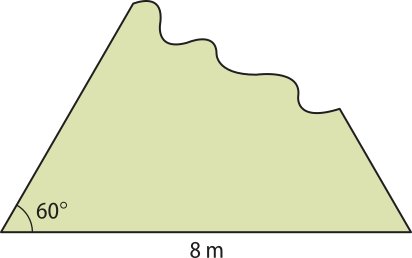
Os lados do triângulo quê não aparécem totalmente na planta do terreno médem:
a) m e (12 − ) m.
b) 5 m e 7 m.
c) 4,5 m e 7,5 m.
d) 8 m e 4 m.
e) 3 m e 9 m.
alternativa b
15. (Mack-SP) Três ilhas A, B e C aparécem num mapa em escala 1∶10.000, como na figura.
Das alternativas, a quê melhor se aproxima da distância entre as ilhas A e B é:
alternativa e
a) 2,3 km.
b) 2,1 km.
c) 1,9 km.
d) 1,4 km.
e) 1,7 km.
Página cento e noventa
16. (Enem/MEC) Uma desenhista projetista deverá desenhar uma tampa em forma circular. Para realizar esse desenho, ela dispõe, no momento, de apenas um compasso, cujo comprimento das hastes é de 10 cm, um transferidor e uma fô-lha de papel com um plano cartesiano. Para esboçar o desenho dessa tampa, ela afastou as hastes do compasso d fórma quê o ângulo formado por elas fosse de 120°. A ponta-seca está representada pelo ponto C, a ponta do grafite está representada pelo ponto B e a cabeça do compasso está representada pelo ponto A conforme a figura.
Após concluir o desenho, ela o encaminha para o setor de produção. Ao receber o desenho com a indicação do raio da tampa, verificará em qual intervalo êste se encontra e decidirá o tipo de material a sêr utilizado na sua fabricação, de acôr-do com os dados.
Tipo de material |
Intervalo de valores do raio (cm) |
|---|---|
I |
0 < R ≤ 5 |
II |
5 < R ≤ 10 |
III |
10 < R ≤ 15 |
IV |
15 < R ≤ 21 |
V |
21 < R ≤ 40 |
Considere 1,7 como aproximação para .
O tipo de material a sêr utilizado pelo setor de produção será:
a) I.
b) II.
c) III.
d) IV.
e) V.
alternativa d
17. (UEA-AM) Considere quê em uma circunferência de raio R está inscrito um triângulo quê tenha um ângulo de medida (alfa)" ôpôsto a um lado do triângulo de medida (éli)", conforme figura 1. A lei dos senos afirma quê (éli)" = 2R ⋅ sen (alfa)".
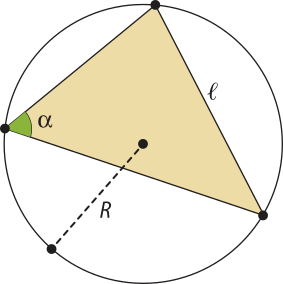
Um triângulo quê tem um lado de medida aproximadamente igual a 7,9 cm está inscrito em uma circunferência de raio 4 cm, conforme mostra a figura 2.
Sabendo quê sen (beta)" = , o perímetro do triângulo da figura 2 é, aproximadamente,
a) 19 cm.
b) 19,4 cm.
c) 19,9 cm.
d) 20,5 cm.
e) 21 cm.
alternativa b
18. (Unicamp-SP) Considere o triângulo retângulo ABD exibido na figura abaixo, em quê AB = 2 cm, BC = 1 cm e cê dê = 5 cm. Então, o ângulo θ é igual a:

a) 15°
b) 30°
c) 45°
d) 60°
alternativa c
Página cento e noventa e um
19. (IFRR) A figura abaixo mostra um triângulo ABC, reto em A, com D pertencente ao lado AC e AD = 3. Além díssu, as retas e formam com a reta ângulos agudos de medidas iguais a 60° e 30°, respectivamente. Se p e q são as áreas dos triângulos BCD e ABD, respectivamente, então, pode-se afirmar quê:
a) p = 2,5q
b) p = 2q
c) p =
d) p =
e) p =
alternativa b
20. (UFRGS-RS) Na figura abaixo, tem-se um retângulo ABCD, de lados AB = 3 e AD = 5, e um triângulo equilátero BEC, construído sobre o lado .
A medida de é
a) .
b) .
c) 7.
d) .
e) .
alternativa e
PARA REFLETIR
Neste Capítulo, estudamos os conceitos de arco de circunferência e de ângulo central e estudamos como medir arcos e ângulos. Também estudamos as unidades de medida usadas para fazer essas medições. Conhecemos a circunferência trigonométrica e como associar os números reais a pontos dessa circunferência.
Estudamos também as relações trigonométricas seno, cosseno e tangente para qualquer arco da circunferência trigonométrica e as relações entre essas razões.
Em seguida, para determinar a medida dos lados e dos ângulos de um triângulo qualquer, aplicamos a lei dos cossenos e a lei dos senos. Por fim, pudemos determinar a área de um triângulo qualquer usando a Trigonometria.
Vamos refletir a respeito das aprendizagens do Capítulo 5:
• Você já conhecia alguns dos conteúdos apresentados ao longo dêste Capítulo? Qual(is)?
• dêz-creva a circunferência trigonométrica e como podemos associar os números reais a pontos dessa circunferência.
• dêz-creva o aprofundamento obtído neste Capítulo em relação ao quê você conhecia sobre as razões trigonométricas seno, cosseno e tangente.
• Mostre uma situação em quê póde sêr usada a lei dos senos e a lei dos cossenos.
• Quais dados são necessários para determinar a área de um triângulo ABC por meio da relação trigonométrica seno?
Respostas pessoais.
Página cento e noventa e dois

