Resoluções das atividades
Capítulo 1 • Pesquisa estatística
Atividades
1. a) População quilombola
Região |
freqüência absoluta |
freqüência relativa |
|---|---|---|
Norte |
166 069 |
12,507% |
Nordeste |
905 415 |
68,189% |
Centro-Oeste |
44 957 |
3,386% |
sudéste |
182 305 |
13,730% |
Sul |
29 056 |
2,188% |
Total |
1 327 802 |
100% |
CAMPOS, Ana Cristina. Censo 2022: Brasil tem 1,32 milhão de quilombolas. Agência Brasil, Brasília, DF, 27 jul. 2023. Disponível em: https://livro.pw/esumr. Acesso em: 31 ago. 2024.
b) Dos 5.568 municípios brasileiros, 1.696 tí-nhão moradores quilombolas. Assim:
100% ≃ 30,46%
Logo, aproximadamente 30,46% dos municípios brasileiros têm moradores quilombolas.
c) Não, pois, de acôr-do com o texto, da população de 1.327.802 quilombolas no Brasil, 15.999 moram em Senhor do Bonfim (BA), cujo percentual do total de quilombolas corresponde a:
⋅ 100% ≃ 1,2%.
d) Os dois estados em quê não há territórios quilombolas oficialmente demarcados são Ácri e Roraima, localizados na Região Norte do Brasil.
e) Resposta pessoal. Espera-se quê os estudantes respondam quê sim, pois a pesquisa é censitária, isto é, todos os indivíduos da população-alvo foram entrevistados.
2. Resposta pessoal. Respostas possíveis: Pesquisa censitária: número de habitantes de uma cidade e perfil socioeconômico dos participantes de um concurso público; pesquisa amostral: pesquisa de opinião sobre a qualidade de um produto e pesquisa de intenção de voto em uma eleição. Há outras respostas possíveis.
3. O senador 2. A amostra não representa a população do país, pois ela não foi selecionada d fórma aleatória e apenas as pessoas quê tí-nhão conhecimento e interêsse no novo projeto responderam à enquete.
4. Amostra sistemática. Há uma regra estabelecida (senhas com números múltiplos de 15), mas se mantém a aleatoriedade (não é possível saber o perfil das pessoas quê foram ao banco).
5. O percentual do total de estudantes quê participaram da pesquisa é:
100% = 20%
Calculando esse percentual em relação a cada estrato, obtém-se:
• 0,2 ⋅ 535 = 107 (homens);
• 0,2 ⋅ 750 = 150 (mulheres).
Logo, participaram da pesquisa 107 homens e 150 mulheres.
Resposta: alternativa a.
6. a) Resposta pessoal. Espera-se quê os estudantes respondam quê sim, pois 13% das vítimas sofreram a primeira ocorrência de agressão até os 14 anos, 17% sofreram na faixa dos 15 aos 18 anos e 22% sofreram na faixa entre 19 e 24 anos.
b) É uma variável quantitativa, pois é indicada por um número.
7. a) A margem de êrro da pesquisa é de 2%. Logo, o intervalo de confiança da intenção de votos do candidato B é
[14,96%; 18,96%], pois:
16,96% − 2% = 14,96%
16,96% + 2% = 18,96%
b) Não. A pesquisa estima quê a intenção real x de votos para o candidato A pertence ao intervalo [24,76%; 28,76%], enquanto a intenção real y de votos para o candidato B pertence ao intervalo [24,67%; 28,67%]. Desse modo, não é possível saber se x é maior do quê, menor do quê ou igual a y. Assim, não há certeza de quê o candidato A vencerá as eleições.
c) 0,1696 ⋅ 2.040 = 345,984 ≃ 346
Logo, o candidato B teve aproximadamente 346 votos.
d) (0,0520 + 0,0480 + 0,0868) ⋅ 2.040 = 381,072 ≃ 381
Portanto, aproximadamente 381 pessoas responderam votos nulos/brancos, estão indecisas ou não opinaram.
8. Ao analisar os gráficos I e II, observa-se quê os pontos correspondentes destacados, referentes ao número de linhas telefônicas em determinados meses, coincidem em ambas as representações. A diferença entre elas é na escala adotada, onde o gráfico I tem, no eixo vertical, intervalos de 50 em 50 unidades de linhas telefônicas representados sem indicação de quebra de escala entre 0 (zero) e 2.000 em comparação com o gráfico II, no qual os intervalos de 50 em 50 unidades de linhas telefônicas estão representados a partir de 2.000. Além díssu, no eixo horizontal, determinados meses estão representados com distância maior entre eles em comparação aos espaçamentos do gráfico II. Desse modo, para um leitor menos atento ou quê não possua a habilidade de leitura de gráficos totalmente desenvolvida, no gráfico I é gerada a impressão de quê o número de linhas telefônicas aumentou pouco ao longo dos meses em comparação ao gráfico II.
Resposta: alternativa d.
9. A soma indica o total de pessoas entrevistadas quê responderam “sim”, ou seja, quê já fizeram uma cirurgia. A média indica a fração de pessoas entrevistadas quê já fizeram alguma cirurgia.
10. a) As informações necessárias são: quem contratou a pesquisa, quem a pagou, a origem e o valor dos recursos, a metodologia utilizada, o plano amostral, o questionário completo, o nível de confiança, a margem de êrro, o período da côléta dos dados e o nome do profissional estatístico responsável pela pesquisa.
b) Estratificada, pois o plano amostral apresenta a ponderação quanto a gênero, idade, grau de instrução e nível econômico dos entrevistados.
c) Enquetes e sondagens não têm plano amostral, isto é, sua amostra não é representativa da população-alvo, e não utilizam metodologia científica. Logo, seus resultados podem sêr equivocados e tendenciosos, ou seja, ilustram um retrato parcial, e não completo, da realidade.
11. a) Amostral, pois foram entrevistadas 1.000 pessoas, e não toda a população.
b) Por telefone.
c) 90%. Espera-se quê os estudantes respondam quê a notícia diz quê nove em cada dez brasileiros apoiam a regulamentação das rêdes, portanto:
= 0,9 = 90%
Página trezentos e cinquenta e cinco
12. Espera-se quê os estudantes, após a realização da pesquisa, quê póde ou não envolver temas relacionados à cultura juvenil, a depender da escolha de cada grupo, compartilhem com a comunidade escolar os resultados da pesquisa.
13. a) Isaúde = ≃ 0,392
Logo, o índice de saúde em 1940 foi, aproximadamente, 0,392.
b) Seja x a expectativa de vida em um país.
1 = ⇒ x = 85
Logo, para quê o índice de saúde de um país seja 1, a expectativa de vida nesse país deve sêr 85 anos.
14. O í dê agá ême é calculado pela raiz cúbica do produto dos índices de educação, longevidade e renda. Logo:
í dê agá ême = ≃ 0,766
Portanto, o í dê agá ême do Brasil, em 2021, foi 0,766.
15. A região do Brasil com melhor distribuição de renda é aquela quê apresenta o menor índice de Gini, sêndo, neste caso, a Região Sul.
Resposta: alternativa d.
16. O PIB per cápita (em R$) total da região, com população (em milhões) por estado, é calculado da seguinte maneira:
1 ⋅ 15.000 + 8 ⋅ 15.000 + 3 ⋅ 30.000 + 15 ⋅ 30.000 = 675.000
Logo, o PIB per cápita (em R$) dessa região é dado por:
= 25.000
Resposta: alternativa d.
17. De acôr-do com o gráfico, a diferença nacional entre a expectativa de vida de mulheres e homens é, aproximadamente, 7 anos. Os dois estados quê apresentam uma diferença maior do quê 7 anos são baía (BA) e Alagoas (AL).
Resposta: alternativa e.
18. A expectativa de vida do brasileiro subiu 0,3 ano, pois:
74,9 − 74,6 = 0,3
Em um ano, há 12 meses, e cada mês foi fixado em 30 dias, logo o cálculo correto é:
0,3 × 12 × 30 ⇒ 3,6 × 30
Resposta: alternativa c.
19. Substituindo na fórmula do CDRS os dados apresentados no gráfico e no enunciado, temos:
CDRS = 1 − ≃ 0, 16
Resposta: alternativa b.
20. As médias aritméticas do í dê agá ême dos municípios são:
São Caetano do Sul (SP): = 0,82
Águas de São Pedro (SP): = 0,76
Florianópolis (SC): = 0,75
Balneário Camboriú (SC): = 0,79
Vitória (ES): = 0,76
O município com a menor média foi Florianópolis, sêndo êste o escolhido pela ôngui.
Resposta: alternativa a.
21. A média é 32 anos, pois:
= ⋅ 30 + ⋅ 35 = 32
Portanto, a cidade receberá o recurso III.
Resposta: alternativa c.
22. Como nenhum país zerou ou atingiu o índice mássimo, então X é maior do quê 0 e menor do quê 1. Sendo assim, nas potências de base X, quanto menor o expoente, maior o valor da potência.
Desse modo, temos:
> > X > X2 > X3
Logo, o país com maior IDH é o terceiro.
Resposta: alternativa c.
23. Consideremos y o PIB e z a população do país X em 2021. Em 2022, o PIB per cápita dêêsse país foi:
≃ 1,073 ⋅
Assim, o PIB per cápita do país X cresceu, aproximadamente, 7%.
Resposta: alternativa c.
24. Atividade de pesquisa: oriente os estudantes a como fazer uma pesquisa. Para orientá-los, recomenda-se a leitura do seguinte artigo: MACHADO, Daniela. Aprender a pesquisar e pesquisar para aprender. São Paulo: Instituto Palavra Aberta, 7 nov. 2019. Disponível em: https://livro.pw/imjcb. Acesso em: 4 out. 2024.
Respostas possíveis de ações: para contribuir com a melhoria do índice de educação, podem sêr promovidas políticas públicas de ampliação do número de escolas e investimento em suas infraestruturas; para o aumento do índice de longevidade, podem sêr feitas melhorias em saneamento básico, ampliação de setores hospitalares e criação de programas quê incentivam a formação de novos profissionais da saúde na região; para a melhoria do índice de renda, podem sêr promovidas ações de aumento e manutenção de empregos e programas de auxílio de distribuição de renda. Há outras ações possíveis.
Atividades complementares
1. A quantidade total de funcionários da empresa representa o conjunto dos indivíduos com o qual se deseja fazer o experimento, ou seja, a população dele. O consumo de litros de á gua por funcionário é o quêstionamento do experimento, que póde admitir valores não inteiros, sêndo, assim, uma variável contínua da pesquisa. Os funcionários escolhidos arbitrariamente são uma parte da população, ou seja, uma amostra dela; como os funcionários foram escolhidos arbitrariamente, com uma mesma probabilidade de escolha dos demais, esse experimento consiste em uma amostragem aleatória simples.
Resposta: alternativa d.
2. Como a margem de êrro da pesquisa é 3%, o percentual de votos dos candidatos X, Y e Z pertence, respectivamente, aos intervalos [33%; 39%], [30%; 36%] e [28%; 34%]. Caso o candidato Z tenha 34% e o candidato X, 33%, o candidato Z poderia vencer com uma diferença de, no mássimo, 1% sobre X.
Resposta: alternativa d.
3. A razão entre as colunas B e A no gráfico 1 é .
A razão entre as colunas B e A no gráfico 2 é
Efetuando a diferença entre as razões, temos:
Resposta: alternativa e.
4. Segundo o texto e os dados apresentados, o IDH do Brasil:
• de 1990 a 2000 teve aumento de 0,065;
• de 2000 a 2010 teve aumento de 0,050.
Assim, a variação dêêsses aumentos, a cada dez anos, não foi proporcional e foi decrescente.
Resposta: alternativa c.
5. Nos municípios X e Z, ao longo da década de 1990, os índices do IDH quê aumentaram estão relacionados à longevidade e à educação. Nesse mesmo período, no município Y, houve um aumento dos três tipos de índice do IDH (renda, longevidade e educação). Logo, as políticas bem implementadas nos três municípios foram II e III, apenas.
Resposta: alternativa d.
Página trezentos e cinquenta e seis
6. A média de casos confirmados em todas as regiões é dada por:
= 229
Em 5 regiões, o número de casos é maior do quê a média de casos, enquanto nas outras 3, o número de casos é inferior à média. Assim, o número de funcionários quê a prefeitura deverá contratar é 71, pois:
5 ⋅ 10 + 3 ⋅ 7 = 71
Resposta: alternativa d.
7. É possível observar no gráfico de radar, quê o gênero “Infantil” vendeu 30 obras em 2020 e em 2021. O gênero Biografias também vendeu 30 obras em 2020 e em 2021.
Resposta: alternativa d.
8. Calculando a média de cada estudante, temos:
(André)
(Beatriz)
(Cecília)
(Daniel)
Logo, Cecília teve a maior média das notas nas três provas.
Resposta: alternativa c.
9. a) Atividade de pesquisa: oriente os estudantes acerca dos problemas relacionados a não indicar fontes consultadas e ao plágio. Para orientá-los, recomenda-se a leitura do seguinte material: BATISTA, Andreza Pereira éti áu. Para o plágio eu digo não!: guia de boas práticas. Fortaleza: UFC, 2021. Disponível em: https://livro.pw/uhgdv. Acesso em: 4 out. 2024.
b) Resposta pessoal. Algumas instituições de ensino superior com vestibular específico para povos indígenas, conforme especificado em seus sáites, em 2024, são: UFRR, UFPE, UnB-DF, Unicamp-SP e UFSM-RS.
Capítulo 2 • Progressões
Atividades
1. Para representar as sequências, vamos considerar os quatro primeiros termos, ou seja, aqueles cujos índices são 1, 2, 3 e 4.
a) an = 3n − 1
a1 = 3 ⋅ 1 − 1 = 2; a2 = 3 ⋅ 2 − 1 = 5;
a3 = 3 ⋅ 3 − 1 = 8; a4 = 3 ⋅ 4 − 1 = 11
(2, 5, 8, 11, …)
b) an = 2n−1
a1 = 21−1 = 1; a2 = 22−1 = 2;
a3 = 23−1 = 4; a4 = 24−1 = 8
(1, 2, 4, 8, …)
c) an = 1 + (−1)n
a1 = 1 + (−1)1 = 0; a2 = 1 + (−1)2 = 2;
a3 = 1 + (−1)3 = 0; a4 = 1 + (−1)4 = 2
(0, 2, 0, 2, …)
d) an = n2 − 1
a1 = 12 − 1 = 0; a2 = 22 − 1 = 3;
a3 = 32 − 1 = 8; a4 = 42 − 1 = 15
(0, 3, 8, 15, …)
2. a) Calcular o quinto e o oitavo termos de uma sequência equivale considerar n = 5 e n = 8, respectivamente. Logo:
a5 = 3 ⋅ 5 + 1 ⇒ a5 = 16
a8 = 3 ⋅ 8 + 1 ⇒ a8 = 25
b) Para determinar a ordem (posição) de um termo, no caso, 49, deve-se considerar an = 49 e, em seguida, calcular o valor de n. Logo:
49 = 3n + 1 ⇒ n = 16
Portanto, o termo 49 ocupa a 16ª posição dessa sequência.
c) Considerando an = 1.001, para quê esse termo pertença a essa sequência, deve-se ter, necessariamente, um valor de n natural. Assim:
1.001 = 3n + 1 ⇒ n =
Como n ∉ ℕ*, conclui-se quê 1.001 não é um termo dessa sequência.
3. a) Considerando n = 100, obtém-se: f(100) = 2 ⋅ 100 − 1 = 199.
b) Considerando an = 99, obtém-se: 99 = 2n − 1 ⇒ n = 50.
Portanto, o número 99 ocupa a 50ª posição dessa sequência.
c) Calculando cada termo da sequência, conforme o enunciado, obtêm-se:
f(1) + f(7) = 2 ⋅ 1 − 1 + 2 ⋅ 7 − 1 = 1 + 13 = 14
f(2) + f(6) = 2 ⋅ 2 − 1 + 2 ⋅ 6 − 1 = 3 + 11 = 14
f(3) + f(5) = 2 ⋅ 3 − 1 + 2 ⋅ 5 − 1 = 5 + 9 = 14
Portanto, conclui-se quê a soma é sempre igual a 14.
4. a) Se a1 = 3 e an = 2an − 1 − 5, então:
a2 = 2a1 − 5 = 2 ⋅ 3 − 5 = 1
a3 = 2a2 − 5 = 2 ⋅ 1 − 5 = −3
a4 = 2a3 − 5 = 2 ⋅ (−3) − 5 = −11
(3, 1, −3, −11, …)
b) Se a1 = 2 e an = (an − 1)2, então:
a2 = (a1)2 = (2)2 = 4
a3 = (a2)2 = (4)2 = 16
a4 = (a3)2 = (16)2 = 256
(2, 4, 16, 256, …)
c) Se a1 = 2 e an = então:
a2 =
a3 = = 2
a4 =
(2, , 2, ,…)
d) Se a1 = 0 e an = então:
a2 = = 1
a3 =
a4 =
(0, 1, , , …)
• Resposta possível:
No item a, o 1º termo é 3, e cada termo a partir do 2º é obtído pela diferença entre o dôbro do termo anterior e 5.
No item b, o 1º termo é 2, e cada termo a partir do 2º é obtído pelo quadrado do termo anterior.
No item c, o 1º termo é 2, e cada termo a partir do 2º é obtído pelo inverso do termo anterior.
No item d, o 1º termo é 0, e cada termo a partir do 2º é obtído pela raiz quadrada da soma do termo anterior com 1.
5. a) Ao observar a sequência das macieiras, pode-se escrever a1 = 1, a2 = 4, a3 = 9 e a4 = 16. Portanto, o termo geral é an = n2. De forma análoga, ao analisar a sequência dos pinheiros, tem-se a1 = 8, a2 = 16, a3 = 24 e a4 = 32. Portanto, o termo geral é an = 8n.
b) O número de macieiras será maior do quê o número de pinheiros quando:
n2 > 8n ⇒ n2 − 8n > 0
Resolvendo a equação n2 − 8 = 0, obtém-se n(minutos)" = 0 e n” = 8

Portanto, n < 0 ou n > 8.
Como devemos considerar n um número natural, pois o valor de n indica a quantidade de macieiras, logo um valor positivo, tem-se n > 8.
Assim, o número de macieiras será maior do quê o número de pinheiros a partir de n = 9.
Página trezentos e cinquenta e sete
6. a) Considere 5 o termo central, portanto 25 e 1 serão os outros dois termos.
Então 5 ≠ e, portanto, a sequência não é uma PA.
b) Como todos os termos são iguais, a sequência é uma PA constante de razão 0.
c) Em uma PA, a razão é constante e dada por:
r = an + 1 − an
Na sequência dada, observa-se quê:
30 − 36 = 24 − 30 = 18 − 24 = −6
Portanto, a sequência é uma PA de razão −6.
d) Considere 16 o termo central, portanto 13 e 20 serão os outros dois termos. Então 16 ≠ e, portanto, a sequência não é uma PA.
e) Em uma PA, a razão é constante e dada por:
r = an + 1 − an
Na sequência dada, observa-se quê:
9 − 2 = 16 − 9 = 23 − 16 = 30 − 23 = 7
Portanto, a sequência é uma PA de razão 7.
7. a) Como o primeiro termo é 10 e a razão é 3, então: (10, 13, 16, 19, 22).
b) Como o primeiro termo é −3 e a razão é 5, então: (−3, 2, 7, 12, 17, 22).
c) Como o primeiro termo é a + 2 e a razão é a, então: (a + 2, 2a + 2, 3a + 2, 4a + 2).
8. Uma sequência será uma PA quando a razão da progressão for constante.
a) an = 3n − 1
r = an + 1 − an
r = 3(n + 1) − 1 − (3n − 1) = 3n + 3 − 1 − 3n + 1 = 3
Portanto, é uma PA de razão 3.
b) an = n2
r = an + 1 − an
r = (n + 1)2 − n2 = n2 + 2n + 1 − n2 = 2n + 1
Portanto, não é uma PA, pois a diferença entre os termos não é constante.
9. Sejam r a razão da PA e a seu primeiro termo. Como a é o termo anterior a 11 e sabendo quê 20 é o quinto termo, utilizando o termo geral da PA, tem-se:
20 = a + 4r ⇒ 20 = 11 − r + 4r ⇒ r = 3
Assim, conclui-se quê:
a = 11 − 3 = 8 e c = 20 − r = 20 − 3 = 17
Pelo teorema de Pitágoras, sêndo 17 cm a medida da hipotenusa e 8 cm a medida de um dos catetos, o outro terá a medida de 15 cm.
Resposta: alternativa d.
10. Para calcular o vigésimo termo de uma PA, é necessário ter o valor da razão e do primeiro termo. Pelo enunciado, sabe-se quê a1 = −8. Assim, para obtêr a razão, fazemos:
r = −3 − (−8) = 5
Utilizando o termo geral de uma PA, obtém-se:
an = a1 + (n − 1) ⋅ r ⇒ a20 = −8 + 19 ⋅ 5 = 87
11. Como o enunciado fornece os valores da razão da progressão e, também, do primeiro termo da PA, pode-se utilizar o termo geral para calcular a posição do termo igual a 44. Sendo assim:
an = a1 + (n − 1) ⋅ r ⇒ 44 = 4 + (n − 1) ⋅ 5 ⇒ n = 9
Portanto, o termo 44 ocupa a 9ª posição dessa PA.
12. Para determinar o termo geral de uma PA, é necessário conhecer o primeiro termo e a razão. Como o enunciado forneceu os dois primeiros termos da PA, tem-se quê:
r = 7 − 2 = 5
Como a1 = 2, obtém-se:
an = a1 + (n − 1) ⋅ r ⇒ an = 2 + (n − 1) ⋅ 5 ⇒ an = 5n − 3
13. Os números ímpares são (1, 3, 5, …), portanto a1 = 1 e r = 2, pois r = 3 − 1 = 2. Assim, o 60º número ímpar será o termo a60. Logo:
an = a1 + (n − 1) ⋅ r ⇒ a60 = 1 + (60 − 1) ⋅ 2 ⇒ a60 = 119
14. Analisando a PA, é possível identificar quê a1 = 5 e r = 5, pois r = 10 − 5 = 5. Como an = 785, pode-se utilizar o termo geral da PA para calcular o valor de n, quê, nesse caso, equivale à quantidade de termos da PA. Portanto:
an = a1 + (n − 1) ⋅ r ⇒ 785 = 5 + (n − 1) ⋅ 5 ⇒ 5n = 785 ⇒ n = 157
Sendo assim, a PA tem 157 termos.
15. Para determinar um termo qualquer de uma PA, é necessário saber o primeiro termo dessa PA e a razão para, então, utilizar o termo geral. Sendo assim:
a) a1 = 6,5
r = 7,0 − 6,5 = 0,5
an = a1 + (n − 1) ⋅ r ⇒ a15 = 6,5 + (15 − 1) ⋅ 0,5 ⇒ a15 = 13,5
b) a1 = 3 +
r = 4 − (3 + ) = 1 −
an = a1 + (n − 1) ⋅ r ⇒ a20 = 3 + + (20 − 1) ⋅ (1 − ) ⇒ a20 = 22 −
c) a1 = 1 + (pi)" e
r = −1 + 2(pi)" − (1 + (pi)") = −2 + (pi)"
an = a1 + (n − 1) ⋅ r ⇒ a10 = 1 + (pi)" + (10 − 1) ⋅ (−2 + (pi)") ⇒ a10 = −17 + 10(pi)"
• Uma resposta possível seria utilizar, por exemplo, a1 = e a2 = e pedir o cálculo de a5. Assim:
a1 = e r =
an = a1 + (n − 1) ⋅ r ⇒ a5 = + (5 − 1) ⋅ ⇒ a5 =
16. Construindo um esboço quê represente a situação do enunciado, tem-se:
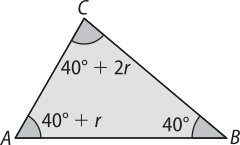
Portanto:
40°+ 40° + r + 40° + 2r = 180° ⇒ r = 20°
Logo, os outros dois ângulos médem:
= 40° + 20° = 60°
= 40° + 40° = 80°
17. Considerando os dados fornecidos pelo enunciado, sabe-se quê a8 = 16 e a10 = 20. Sendo assim, utilizando o termo geral da PA, obtém-se o sistema:
Subtraindo a segunda equação da primeira, obtém-se r = 2. Substituindo esse resultado em qualquer uma das equações, tem-se a1 = 2.
Portanto, a1 = 2 e r = 2.
18. De acôr-do com a figura, é possível observar quê:
Assim: a1 = 3, r = 2 e n = 100.
Então: a100 = 3 + 99 ⋅ 2 ⇒ a100 = 201.
Serão necessários 201 palítos para construir 100 triângulos.
Página trezentos e cinquenta e oito
19. Considerando as informações do sistema, pode-se reescrevê-lo a partir da definição de PA.
Logo:
Resolvendo o sistema, obtêm-se r = 3 e a1 = −1.
Portanto, a PA é dada por (−1, 2, 5, …).
20. A atividade trata de uma PA composta de 5 termos. Sendo assim, consideram-se os termos como a1 = x − 2r, a2 = x − r, a3 = x, a4 = x + r e a5 = x + 2r para auxiliar os cálculos.
De acôr-do com as informações do enunciado, obtém-se o seguinte sistema:
Logo:
Substituindo (II) em (I):
64 = 28 + 4r2 ⇒ 4(r2 − 9) = 0
Resolvendo a equação do 2º grau, obtêm-se as raízes r(minutos)" = 3 e r” = −3. Como a razão é um número positivo, pois a PA é crescente, então deve-se desconsiderar a raiz negativa.
Calculando os termos da PA:
a1 = 8 − 2 ⋅ 3 = 2
a2 = 8 − 3 = 5
a3 = 8
a4 = 8 + 3 = 11
a5 = 8 + 2 ⋅ 3 = 14
Logo, os números quê formam a PA são (2, 5, 8, 11, 14).
21. a) Considerando a PA descrita no enunciado, pode-se afirmar quê a1 = 4 e r = 3, pois r = 7 − 4. Sendo assim, o termo geral dessa PA é an = 4 + (n − 1) ⋅ 3 ou simplesmente an = 3n + 1.
Portanto, a PA póde sêr associada à função cuja lei é f(x) = 3x + 1.
b) O domínio dessa função são os números naturais maiores do quê zero (ℕ*), e a imagem é a própria sequência da PA, ou seja, Im(f) = {4, 7, 10, 13, 16, …}.
22. Pode-se organizar as informações do enunciado em um qüadro, para ajudar a compreender a situação.
freqüência |
87,9 |
88,1 |
… |
107,9 |
|---|---|---|---|---|
Canal |
200 |
201 |
… |
x |
Os números formam uma PA cujo primeiro termo é a1 = 87,9 e o último, an = 107,9. Além díssu, sabe-se quê r = 0,2.
a) Considerando a fórmula do termo geral, obtém-se:
an = a1 + (n − 1)r ⇒ 107,9 = 87,9 + (n − 1) ⋅ 0,2 ⇒ 20 = (n − 1) ⋅ 0,2 ⇒ 100 = n − 1 ⇒ n = 101
Portanto, podem funcionar 101 emissoras.
Para calcular o número do canal com maior freqüência, deve-se considerar a PA cujo primeiro termo é a1 = 200,
n = 101 e r = 1.
a101 = 200 + (101 − 1) ⋅ 1 ⇒ a101 = 300
Portanto, o número do canal com maior freqüência é 300.
b) Deve-se calcular a86 na PA quê representa a sequência de freqüências, pois, como a1 corresponde ao canal 200, então o canal 285 será a86.
a86 = 87,9 + (86 − 1) ⋅ 0,2 ⇒ a86 = 87,9 + 85 ⋅ 0,2 = 104,9
Então, a freqüência do canal 285 é 104,9 MHz.
23. A atividade trata de uma PA de razão 2 com cinco termos.
Considerando a1 como o primeiro termo, os demais podem sêr representados por:
a2 = a1 + 2
a3 = a1 + 4
a4 = a1 + 6
a5 = a1 + 8
Com base nas informações do enunciado, tem-se:
a1 + a1 + 2 + a1 + 4 + a1 + 6 + a1 + 8 = 110 ⇒ 5a1 = 110 − 20 ⇒ a1 = 18
Logo, 18 cm é a altura do menor livro.
Resposta: alternativa d.
24. Analisando as duas primeiras parcelas, nota-se quê a razão da PA é r = 6, pois 126 − 120 = 6.
Sabendo o valor da primeira parcela e a razão da PA, encontram-se os valores, em reais, da 19ª parcela quê Joana não pagou e da última parcela paga por ela:
a19 = a1 + (n − 1) ⋅ r ⇒ a19 = 120 + 18 ⋅ 6 ⇒ a19 = 228
a24 = a1 + (n − 1) ⋅ r ⇒ a24 = 120 + 23 ⋅ 6 ⇒ a24 = 258
Assim, o valor total pago por Joana, segundo o enunciado, será a soma das 24 parcelas, com exceção da 19ª:
S24 − a19 = − a19 = − 228 = 4.308
Portanto, R$ 4.308,00 foi o valor total pago por Joana.
Resposta: alternativa d.
25. Como a razão de uma PG é, a partir do segundo termo, o quociente entre cada termo e o respectivo antecessor, pode-se concluir quê:
a) q = ⇒ q = 4
b) q = ⇒ q = −3
c) q = ⇒ q =_
d) q = ⇒ q = 24
e) q = ⇒ q =
f) q = ⇒ q = 102
26. Segundo os critérios de classificação de uma PG, pode-se afirmar quê:
a) Constante, pois q = 1.
b) Decrescente, pois a1 = 1 e q = .
c) Decrescente, pois a1 = −2 e q = 4.
d) Oscilante, pois a1 = 3 e q = −2.
e) Crescente, pois a1 = 4 e q =
f) Crescente, pois a1 = −7 e q = .
27. Para verificar se a sequência an = 5 ⋅ 4n−2 é uma PG, deve-se tentar identificar o termo a1 e a razão q, sêndo a1 ≠ 0 e q uma constante. Assim:
an = 5 ⋅ 4n−2 ⇒ a1 = 5 ⋅ ⇒ a1 =
q = = ⇒ q = 4n−1−n+2 = 4
Portanto, a sequência é uma PG cujo primeiro termo é a1 = e q = 4.
28. A sequência (a, b, c) é uma PA de razão r = 5. Então:
A sequência (a + 2, b, c − 1) é uma PG. Então:
(III)
Substituindo as expressões (I) e (II) na expressão (III), obtém-se:
⇒ a = 7
Substituindo o valor de a nas expressões (I) e (II), obtém-se:
Logo, a + b + c = 36.
Página trezentos e cinquenta e nove
29. Como a sequência (3, a, b) é uma PA crescente, pode-se afirmar quê 3 < a < b.
Além díssu:
a − 3 = b − a ⇒ b = 2a − 3 (I)
Como a sequência (a, b, 8) é uma PG, pode-se afirmar quê:
⇒ b2 = 8a (II)
Substituindo (I) em (II):
(2a − 3)2 = 8a ⇒ 4a2 − 20a + 9 = 0
Resolvendo a equação do 2º grau, obtêm-se as raízes a(minutos)" = e a” = .
Como a > 3, deve-se descartar a segunda raiz.
Substituindo o valor de a em (I), obtém-se b = 6.
Portanto, a = e b = 6.
30. Pelo enunciado, é possível identificar quê a1 = 512 e q = , pois q = .
Então:
a6 = 512 ⋅ ⇒ a6 = 16
31. Pelo enunciado, é possível identificar quê a6 = 2 e q = . Assim:
a6 = a1 ⋅ q5 ⇒ 2 = a1 ⋅ ⇒ a1 = 2.048
32. Pelo enunciado, têm-se a1 = e a7 = 16. Portanto:
a7 = a1 ⋅ q6 ⇒ 16 = ⋅ q6 ⇒ q = ±2
33. Pelo enunciado, têm-se a5 = 32 e a8 = 256.
Dessa forma:
⇒ q3 = 8 ⇒ q = 2
Com o valor de q, é possível calcular a1.
Assim:
a5 = 32 ⇒ a1 ⋅ 24 = 32 ⇒ a1 = 2
34. Com as informações fornecidas pelo enunciado, é possível elaborar o seguinte sistema:
Como a diferença entre a2 e a1 (ou entre a5 e a4)é diferente de zero, então q é diferente de 1.
Aplicando a definição de PG, obtêm-se:
⇒
Ao dividir a segunda equação pela primeira, obtém-se:
![]() = ⇒ q3 = 64 ⇒ q = 4
= ⇒ q3 = 64 ⇒ q = 4
Como a1(q − 1) = 9, então:
3a1 = 9 ⇒ a1 = 3
35. Considerando a1 = 18, então a4 = b, pois foram inseridos dois termos entre eles. Como o enunciado afirma quê a razão é 3, então:
b = a1 ⋅ q3 ⇒ b = 18 ⋅ 33 ⇒ b = 486
36. Pelo enunciado, sabe-se quê a1 = 1 e a2 = 9. Logo:
q = ⇒ q = = 9
Portanto:
an = a1 ⋅ qn−1 ⇒ 6.561 = 1 ⋅ 9n−1 ⇒ 38 = 32(n−1) ⇒ 8 = 2n − 2 ⇒ n = 5
37. Pelo enunciado, sabe-se quê a1 = 5 e a2 = 50. Então:
q = = 10
Assim:
an = 500.000 ⇒ an = 5 ⋅ 105 ⇒ 5 ⋅ 10n−1 = 5 ⋅ 105 ⇒ n − 1 = 5 ⇒ n = 6
Portanto, a soma de todos os termos será:
S6 = ⇒ S6 = 555.555
38. Pelo enunciado, sabe-se quê a1 = 3 e a2 = 6. Dessa forma, q = = 2.
Como a soma de todos os termos é Sn = 765, então:
Sn = ⇒ 765 = ⇒ n = 8
Portanto, 8 termos.
39. Ao analisar a quantidade de tábuas em cada pilha, é possível observar quê se forma a sequência (1, 2, 4, 8, …), uma PG, em quê a1 = 1 e q = 2.
a) Ao final de 9 operações, tem-se:
an = a1 ⋅ qn−1 ⇒ a9 = 1 ⋅ 28 ⇒ a9 = 256
Portanto, 256 tábuas.
b) Como cada tábua tem 0,5 cm de espessura, a altura da pilha, em centimetro, será:
256 ⋅ 0,5 = 128
Portanto, a pilha terá 1,28 m de altura.
40. Pelo enunciado, sabe-se quê a1 = 2 e q = 2; então, ao final de 12 dias, a quantidade de á gua perdida é dada por:
S12 = = 2 ⋅ 4.095 = 8.190 ⇒ S12 = 8.190
Portanto, até o 12º dia, serão perdidos 8.190 litros de á gua.
41. Observando a sequência de cada item, é possível identificar o termo a1 e calcular a razão q.
a) a1 = 5; q =
Portanto, o termo geral é:
an = a1 ⋅ qn−1 ⇒ an = 5 ⋅
Considerando quê a função possui domínio ℕ*, então:
f(n) = 5 ⋅
f(n) = 5 ⋅ = 25 ⋅
A soma de todos os termos é:
S =
b) a1 = 2−2 = ; q = = 2−2 =
Portanto, o termo geral é:
an = a1 ⋅ qn−1 ⇒ an =
Considerando quê a função possui domínio ℕ*, então:
f(n) = ⇒ f(n) =
A soma de todos os termos é:
S =
c) a1 = 9−1; q =
Portanto, o termo geral é:
an = a1 ⋅ qn−1 ⇒ an =
Considerando quê a função possui domínio ℕ*, então:
f(n) = ⇒ f(n) =
A soma de todos os termos é:
S =
42. a)
n |
an = 2n |
|---|---|
1 |
2 |
2 |
4 |
3 |
8 |
4 |
16 |
5 |
32 |
Página trezentos e sessenta
Ao plotar os pontos em um plano cartesiano, obtém-se o seguinte gráfico:
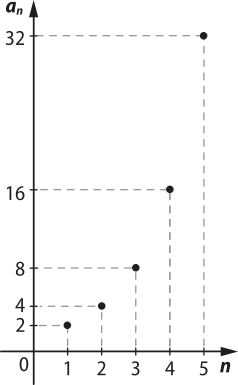
b)
n |
an = |
|---|---|
1 |
3 |
2 |
1 |
3 |
|
4 |
|
5 |
Ao plotar os pontos em um plano cartesiano, obtém-se o seguinte gráfico:

43. Para calcular a soma dos termos de uma PG infinita, é necessário identificar o primeiro termo a1 e a razão q. Assim:
a) a1 = 80x; q =
Pelo enunciado, sabe-se quê a soma de todos os termos do primeiro membro da equação é 320, então:
S = ⇒ 320 = ⇒ 80x = 160 ⇒ x = 2
S = {2}
b) a1 = 5x; q =
Pelo enunciado, sabe-se quê a soma de todos os termos do primeiro membro da equação é , então:
⇒ 125 = 5x ⇒ x = 3
S = {3}
44. Como a bola sobe e desce, deve-se calcular, separadamente, a distância percorrida somente na descida e, em seguida, calcular a distância percorrida somente na subida. A distância percorrida pela bola será a soma dessas duas distâncias. Portanto:
I. Soma das descidas
Primeiro deslocamento de descida:
a1 = 30 e r = .
Logo:
d1 = ⇒ d1 = = 45
II. Soma das subidas Primeiro deslocamento de subida:
a1 = 10 e r = .
Logo:
d2 = ⇒ d2 = = 15
Distância total percorrida:
d = d1 + d2 = 45 + 15 ⇒ d = 60
A distância total percorrida pela bola será de 60 metros.
45. Perímetro é a medida do comprimento do contôrno de uma figura e, no caso apresentado, o perímetro do quadrado corresponde a 4 vezes a medida do lado, já quê a figura é um quadrado.
Para determinar a soma de todos os perímetros da sequência, é necessário o valor do primeiro termo e a razão da sequência. Sendo assim:
a1 = 4(éli)" e a2 = = 2(éli)"
Então:
q =
S = ⇒ S = = 8(éli)"
46. a) Pelo enunciado, sabe-se quê a1 = 5 e a3 = 45. Logo:
a3 = a1 ⋅ q2 ⇒ 45 = 5 ⋅ q2 ⇒ q = ±3
Como a razão é positiva, q = 3.
Sendo assim, a soma dos 6 primeiros termos será:
S6 = ⇒ S6 = ⇒ S6 = 1.820
b) Como 112 é múltiplo de 4, não deve sêr considerado. Assim, a soma dos primeiros 111 números inteiros é:
S111 = = 6.216
Agora, é necessário calcular a soma de todos os números múltiplos de 4 e menóres do quê 112. O maior número múltiplo de 4, dentro do intervalo, é 108, pois 112 − 4 = 108, e o menor é o próprio 4. Sendo assim, tem-se a PA (4, 8, 12, 16, …, 108) de n termos. Desse modo:
108 = 4 + (n − 1) ⋅ 4 ⇒ n = 27
Calculando a soma dos termos:
SM(4) = = 1.512
Assim, a soma de todos os números inteiros positivos menóres do quê 112 e não divisíveis por 4 é:
S = 6.216 − 1.512 = 4.704
c) O 20º termo dessa PA (a20) póde sêr calculado da seguinte maneira:
a20 = S20 − S19
Portanto, utilizando a fórmula fornecida pelo enunciado, obtém-se:
a20 = S20 − S19 ⇒ a20 = 20(2 ⋅ 20 + 1) − 19(2 ⋅ 19 + 1) ⇒ a20 = 79
Atividades complementares
1. Analisando as vendas mensais dos produtos I e II, percebe-se quê cada uma póde sêr expressa por uma PA. A razão nas vendas do produto I é 10 e nas vendas do produto II é igual a −20.
Vendas produto I: (80, 90, 100, 110, 120, 130, …)
Vendas produto II: (190, 170, 150, 130, 110, 90, …)
Nota-se quê, a partir do quinto termo dessas progressões, as vendas do produto I superam as vendas do produto II. Como o termo a1 representa o mês de abril, então o termo a5 representa o mês de agosto. Assim, o gerente cessará a produção do produto II em setembro.
Resposta: alternativa d.
2. Considerando as propriedades de uma PA, pode-se afirmar quê a2 =, logo:
x + 14 = ⇒ 2x + 28 = 11x − 8 ⇒ x = 4
Portanto, a soma dos 3 termos será:
S = 5x − 5 + x + 14 + 6x − 3 = 12x + 6 = 12 ⋅ 4 + 6 = 54
Resposta: alternativa b.
3. Com base nas figuras, é possível notar quê a quantidade de quadrados centrais aumenta de acôr-do com a regra n2, em quê n representa o número da etapa.
Além díssu, há uma quantidade fixa de 4 quadrados quê não varia de etapa para etapa. Assim, pode-se concluir quê a lei quê rege a quantidade de quadrados póde sêr escrita por an = n2 + 4.
Portanto, o número de quadrados na etapa 10 será:
a10 = 102 + 4 = 104
Resposta: alternativa c.
4. Como a PA é formada a partir do segundo dia, pode-se entender quê a sequência de peças montadas diariamente é (40, a1, a2, …, a10). Como há 1.000 peças no total, conclui-se quê a quantidade de peças relacionadas à PA é 960, pois 1.000 − 40 = 960.
Página trezentos e sessenta e um
Como o segundo dia (a1) corresponde a 60% do número de peças montadas no sétimo dia (a6), então:
a1 = 0,6(a6) ⇒ a1 = 0,6(a1 + 5r) ⇒ 0,4a1 = 3r ⇒ a1 = 7,5r
Pode-se também afirmar quê:
a10 = a1 + 9r ⇒ a10 = 7,5r + 9r ⇒ a10 = 16,5r
Como a soma de todos os termos é calculada por S = , conclui-se quê:
960 = ⇒ 24r = 192 ⇒ r = 8
Como o nono dia representa o termo a8 da PA, tem-se:
a8 = a1 + 7r ⇒ a8 = 7,5r + 7r = 14,5 ⋅ 8 = 116
Portanto, no 9º dia foram montadas 116 peças.
Resposta: alternativa c.
5. Os andares trabalhados por João foram (1, 3, 5, 7, …), e os andares trabalhados por Pedro foram (1, 4, 7, 10, …); portanto, os andares quê foram reparados pêlos dois ao mesmo tempo foram (1, 7, 13, …, a20).
Assim, essa sequência possui a1 = 1 e r = 6. Logo, o termo geral será:
an = a1 + (n − 1)r ⇒ an = 6n − 5
Sendo assim, conclui-se quê:
a20 = 6 ⋅ 20 − 5 = 115
Logo, esse edifício possui 115 andares.
Resposta: alternativa d.
6. Como entre 1 e 100 há exatamente 50 números ímpares, segundo o enunciado, a soma de todos os números ímpares entre 1 e 100 será 502.
Resposta: alternativa c.
7. Conforme o enunciado, a produção de televisores dobrou a cada mês em comparação ao mês anterior. Ou seja, a produção mensal corresponde aos termos de uma PG de razão 2, cuja soma dos termos é igual ao número total de televisores produzidos no período.
Sendo assim, é possível concluir quê a1 = x, q = 2 e S11 = 204.700, logo:
S11 = ⇒ 204.700 = ⇒ x = 100
Resposta: alternativa a.
8. Com base no enunciado, é possível construir um sistema:
Aplicando a definição das progressões geométricas, obtém-se:
Dividindo a equação (II) pela equação (I), obtém-se:
q = = 2
Resposta: alternativa d.
9. A partir do enunciado, pode-se afirmar quê o primeiro termo da PG é . A razão póde sêr calculada como:
q = = 5
O último termo é 3.125; então, pode-se afirmar quê:
an = a1 ⋅ qn−1 ⇒ 3.125 = 5−3 ⋅ 5n−1 ⇒ 55 = 5n−4 ⇒ n = 9
Resposta: alternativa e.
10. A partir do enunciado, pode-se afirmar quê o primeiro termo da PG é −7. A razão póde sêr calculada como:
q = = −3
Assim, o sexto termo é:
an = a1 ⋅ qn−1 ⇒ a6 = −7 ⋅ (−3)6−1 ⇒ a6 = 1.701
Resposta: alternativa b.
11. Segundo o enunciado, o sáiti tem um número de acessos diários equivalente ao triplo dos acessos do dia anterior, podendo sêr associado à PG (3, 9, 27, …, 2.187), em quê a1 = 3 e q = 3. Assim, para encontrar o dia em quê o sáiti teve 2.187 acessos, utiliza-se o termo geral, ou seja:
an = a1 ⋅ qn−1 ⇒ 2.187 = 3 ⋅ 3n−1 ⇒ 36 = 3n−1 ⇒ n = 7
Portanto, no dia 7 ocorreram 2.187 acessos.
Resposta: alternativa b.
12. Segundo o enunciado, pode-se interpretar quê o valor do perímetro de cada triângulo, organizado em uma sequência, representará uma PG em quê a1 = 24 e q = .
Portanto, a soma será:
S = ⇒ S = = 48
Resposta: alternativa c.
13. Sabe-se quê a5 = a1 ⋅ q4 e quê a5 = 9 ⋅ a1, então:
a1 ⋅ q4 = 9 ⋅ a1 ⇒ q4 = 9 ⇒ q =
Porém, q = não é conveniente, pois a1 > 0 e a6 = , e, assim, a razão precisa sêr um valor menor do quê zero.
Portanto, q = . Como a6 = a2 ⋅ q4, tem-se:
= a2 ⋅ ⇒ = a2 ⋅ 9 ⇒ a2 =
Portanto, o produto a2 ⋅ a7 será:
a2 ⋅ a7 = a2 ⋅ a6 ⋅ q =
Resposta: alternativa a.
14. Elaborando uma sequência com os 10 termos, a partir das orientações do fluxograma, obtém-se:
(−2,, −2, , −2, ,−2, ,−2 e )
Adicionando todos os valores da sequência, obtém-se −12,5.
Resposta: alternativa e.
15. Considerando an = −250, em relação à sequência da PA, tem-se a1 = −2 e r = −4.
Assim, pode-se afirmar quê:
an = a1 + (n − 1) ⋅ r ⇒ −250 = −2 + (n − 1) ⋅ (−4) ⇒ n = 63
Em relação à sequência da PG, tem-se a1 = 3 e q = 2. Então:
Sn = ⇒ S9 = ⇒ S9 = 1.533 ⇒ s = 1.533
Portanto, s − n = 1.533 − 63 = 1.470.
Resposta: alternativa 02.
16. Observando as figuras, nota-se quê, em cada uma, a partir da segunda, a parte escura equivale a 43_ da parte escura da figura anterior.
Sendo assim, considerando a1 = 1 (área inteira), tem-se:
a1 = 1
a2 = ⋅ a1 = ⋅ 1 =
a3 = ⋅ a2 =
a4 = ⋅ a3 =
a5 = ⋅ a4 =
Logo, a sequência é uma PG de razão
Resposta: alternativa a.
Capítulo 3 • Função definida por mais de uma sentença
Atividades
1. a) Como a porcentagem aplicada é relacionada à faixa de unidades vendidas e instaladas, a função é definida por mais de uma sentença.
b) Do enunciado, sabe-se quê cada alarme custa R$ 120,00. Para calcular o valor utilizando a porcentagem de cada unidade, deve-se realizar o seguinte procedimento:
De 1 a 25: 120 ⋅ = 3,6
De 26 a 50: 120 ⋅ =8,4
De 51 a 75: 120 ⋅ = 14,4
De 76 a 100: 120 ⋅ = 20,4
Mais de 100: 120 ⋅ = 26,4
Página trezentos e sessenta e dois
Agora, com as informações do enunciado, é possível determinar a lei de formação da função, com base no valor fixo recebido acrescido da porcentagem por unidade, no intervalo indicado no qüadro. Portanto:
f(x) =
c) Neste caso, deve-se observar o intervalo em quê se encaixa o valor dado (82 alarmes) e aplicar esse valor na função f correspondente:
f(x) = 1200 + 20,4x ⇒ f(82) = 1200 + 20,4 ⋅ 82 = 2.872,8.
Portanto, o salário foi R$ 2.872,80.
d) Considerando quê o funcionário recebeu R$ 1.502,40 e supondo quê ele vendeu até 25 alarmes, tem-se:
1.502,4 = 1.200 + 3,6x ⇒ 3,6x = 302,40 ⇒ x = 84.
Portanto, como 84 > 25, sabe-se quê o funcionário vendeu mais de 25 alarmes.
Supondo quê ele vendeu de 26 a 50 alarmes, tem-se quê:
1.502,4 = 1.200 + 8,4x ⇒ 8,4x = 302,40 ⇒ x = 36.
Como 25 < 36 ≤ 50, pode-se concluir quê o funcionário vendeu 36 alarmes.
2. a) Como 3 ≤ 3, então utiliza-se:
f(x) = 4x − 1 ⇒ f(3) = 4 ⋅ 3 − 1 = 11
Como 5 ≥ 1, então utiliza-se:
g(x) = −x ⇒ g(5) = −5
Portanto, f(3) − g(5) = 11 − (−5) = 16.
b) Como 0 < 1, então utiliza-se:
g(x) = x2 + 4x + 3 ⇒ g(0) = 02 + 4 ⋅ 0 + 3 = 3
Como −1 ≤ 3, então utiliza-se:
f(x) = 4x − 1 ⇒ f(−1) = 4 ⋅ (−1) − 1 = −5
Portanto, g(0) + 2 ⋅ f(−1) = 3 + 2 ⋅ (−5) = −7.
c) Como 4 > 3, então utiliza-se:
f(x) = x2 + 2 ⇒ f(4) = 42 + 2 = 18
Como 1 ≥ 1, então utiliza-se:
g(x) = −x ⇒ g(1) = −1
Portanto, = −18.
3. a) Como f(x) = 0, então:
Para x < 0: 3x + 4 = 0 ⇒ x =
Para x ≥ 0: x − 2 = 0 ⇒ x = 2
Assim, para f(x) = 0, obtém-se:
x = ou x = 2.
b) Como f(x) = −2, então:
Para x < 0: 3x + 4 = −2 ⇒ x = −2
Para x ≥ 0: x − 2 = −2 ⇒ x = 0
Assim, para f(x) = −2, obtém-se: x = −2 ou x = 0.
4. a) A função f é formada por partes de duas sentenças.
Para traçar o gráfico de f1(x) = −x + 2, pode-se determinar dois pontos pertencentes ao gráfico, anteriores ao extremo x = 1. Como a função f1 é válida para x ≤ 1, a bó-linha é fechada no ponto em quê x = 1. Assim:
x |
f1(x) = −x + 2 |
(x, y) |
|---|---|---|
−2 |
f1(−2) = − (−2) + 2 = 4 |
(−2, 4) |
0 |
f1(0) = − (0) + 2 = 2 |
(0, 2) |
1 |
f1(1) = − (1) + 2 = 1 |
(1, 1) |
Para traçar o gráfico da função f2(x) = −x2 + 2x, pode-se determinar o vértice da parábola, os zeros e outro ponto pertencente ao gráfico, além do extremo x = 1. Como a função f2 é válida para x > 1, a bó-linha é aberta no ponto em quê x = 1.
Assim:
f2(x) = −x2 + 2x, se x > 1
xv = = 1
f2(1) = −(1)2 + 2 ⋅ 1 = −1 + 2 = 1
Para encontrar os zeros da função, considera-se f2(x) = 0. Então:
−x2 + 2x = 0 ⇒ x (−x + 2) = 0 ⇒ x = 0 ou x = 2.
Como x = 0 não faz parte do domínio de f2, então obtém-se o ponto (2, 0).
Além díssu, será necessário calcular mais um ponto para essa função. Considere x = 3:
f2(3) = −(3)2 + 2 ⋅ 3 = −9 + 6 = −3
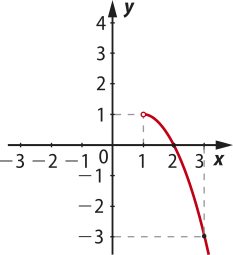
Portanto, reunindo os gráficos de f1 e f2 em um mesmo plano cartesiano, obtém-se o gráfico da função f:
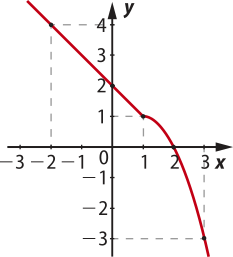
Para determinar o intervalo de decrescimento e crescimento, analisaremos o gráfico construído. Note quê, para quaisquer valores x1 e x2 distintos, em quê x1 < x2, tem-se f(x1) > f(x2). Logo, essa função é decrescente em todo seu domínio.
b) Denotando a primeira sentença da função por g1, tem-se: g1(x) = x2 + 6x + 8, se x ≤ −2.
Para encontrar o vértice da parábola descrita pela função quadrática limitada para x ≤ 2, fazemos:
xv = = −3
g1(−3) = (−3)2 + 6 ⋅ (−3) + 8 = −1
Então, o vértice da parábola descrita pela função limitada g1(x) é V(−3, −1).
Para encontrar os zeros de g1, deve-se resolver a equação x2 + 6x + 8 = 0, cujas raízes são dadas por x(minutos)" = −4 e x(segundos)" = −2.
Determinando mais um ponto do gráfico, considere x = −5: g1(−5) = (−5)2 + 6 ⋅ (−5) + 8 = 3.
Denotando a segunda sentença da função por g2, tem-se: g2(x) = −2x + 3, se x > −2.
Página trezentos e sessenta e três
Para encontrar o zero da função, fazemos g2(x) = 0. Então: −2x + 3 = 0 ⇒ x = = 1,5.
Para identificar o ponto de intersecção com o eixo y, considere x = 0. Então: g2(0) = −2 ⋅ 0 + 3 = 3.
Também calcula-se o valor de g2 para x = −2, quê é o extremo do intervalo: g2(−2) = −2 ⋅ (−2) + 3 = 7.
Compondo os gráficos de g1 e g2 em um mesmo plano cartesiano, temos o gráfico de g(x):
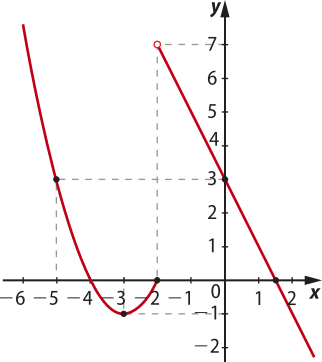
Para determinar o intervalo de decrescimento e crescimento, analisaremos o gráfico construído. Note quê, para quaisquer x1, x2 ∈ [−3, −2] tais quê x1 < x2, tem-se g(x1) < g(x2), ou seja, nesse intervalo, a função é crescente. Já para quaisquer x1, x2 ∈ ]−∞, −3[ tais quê x1 < x2, tem-se g(x1) > g(x2), ou seja, a função é decrescente nesse intervalo. De forma similar, para quaisquer x1, x2 ∈ ]−2, +∞[ tais quê x1 < x2, tem-se g(x1) > g(x2), ou seja, a função também é decrescente nesse intervalo.
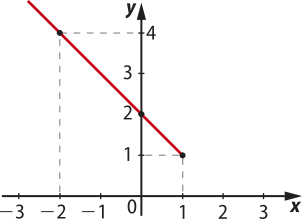
5. Com base na análise do gráfico, percebe-se quê se trata de uma função definida por três sentenças, em quê a primeira delas (g1) corresponde a um trecho de uma função afim decrescente, a segunda sentença (g2) representa um trecho de uma função constante e a terceira sentença (g3) representa um trecho de uma função afim crescente.
A lei geral de formação de uma função afim é g(x) = ax + b, com a, b ∈ ℝ; então, com dois pontos para cada sentença, é possível determinar a lei da função.
Observe quê os pontos (−3, 0) e (−1, −2) fazem parte do gráfico de g1(x) = ax + b.
Substituindo e resolvendo o sistema, obtém-se:
⇒ a = −1 e b = −3
Portanto, g1(x) = −x − 3, para x ≤ −1.
A segunda sentença do gráfico corresponde à função constante g2(x) = −2, para −1 < x ≤ 1.
Os pontos (1, −2) e (3, 0) fazem parte do gráfico de g3(x) = ax + b.
Substituindo e resolvendo o sistema, obtém-se:
⇒ a = 1 e b = −3
Portanto, g3(x) = x − 3, para x > 1.
Assim, a lei de formação da função g póde sêr descrita por:
g(x) =
6. a) Resposta pessoal.
b) Resposta pessoal. Resposta possível: O Programa de Incentivo Social (PIS) e a Contribuição para Financiamento da Seguridade Social (Cofins) são dois tributos quê incidem sobre a receita bruta das empresas. O Imposto sobre Operações relativas à Circulação de Mercadorias e sobre Prestações de Serviços de Transporte Interestadual e de Comunicação (ICMS) é um tributo considerado essencial para os estados, incidindo em quase todas as operações comerciais, como compra de alimentos, elétro domésticos, roupas, combustível etc. A alíquota varia de estado para estado.
c) De acôr-do com a tabéla, a respeito do custo com o valor variável, tem-se os seguintes gastos, em reais, dependendo do consumo:
1 m³ custa: 2,79
3 m³ custam: 2,79 + 2 ⋅ 9,20 = 21,19
7 m³ custam: 21,19 + 4 ⋅ 4,80 = 40,39
14 m³ custam: 40,39 + 7 ⋅ 7,96 = 96,11
Assim, se x representa o consumo, em métro cúbico, e f(x) o valor correspondente a sêr pago, em reais, tem-se quê:
Para 0 < x ≤ 1: f(x) = 9,68 + 2,79x
Para 1 < x ≤ 3: f(x) = 2,79 + 12,64 + 9,20(x − 1) = 15,43 + 9,20(x − 1)
Para 3 < x ≤ 7: f(x) = 21,19 + 12,64 + 4,80(x − 3) = 33,83 + 4,80(x − 3)
Para 7 < x ≤ 14: f(x) = 40,39 + 14,23 + 7,96(x − 7) = 54,62 + 7,96(x − 7)
Para 14 < x ≤ 34: f(x) = 96,11 + 15,81 + 9,46(x − 14) = 111,92 + 9,46(x − 14)
Portanto, a função póde sêr escrita como:
f(x) =
d) Resposta pessoal. Exemplo de situação: Considere quê uma residência consumiu 3,25 m³ de gás natural. Qual será o valor pago por esse consumo?
Calculando o valor da função para x = 3,25, obtém-se: f(3,25) = 33,83 + 4,80 ⋅ (3,25 − 3) = 35,03.
7. a) = 2
b) = 2
c) = 8
d) = 1 + 6 = 7
e) = 5
f) = 2 − 10 = −8
8. a) dAB =
b) dBC =
c) dBD =
d) dAD =
9. a) Para x = −4, temos:
b) Para x = −1, temos:
c) Para x = −2, temos:
10. Do enunciado, tem-se quê: A = . Então, para simplificar essa expressão, precisa-se utilizar a definição de módulo, tal quê:
x| =
|x + 2| =
a) Para x < −2, obtém-se A = −x − (x + 2) = −2x − 2.
b) Para o intervalo −2 ≤ x < 0, obtém-se:
A = −x + (x + 2) = 2.
c) Para x ≥ 0, obtém-se: A = x + (x + 2) = 2x + 2.
Página trezentos e sessenta e quatro
11. Pela definição de módulo, tem-se:
| x + 3| =
| 2x − | =
Então, para x > 3, tem-se:
= x + 3 + 2x − 1 = 3x + 2
12. a) Para calcular o conjunto de valores da expressão , com a, b e c positivos, utilizando a definição de módulo, basta fazer: = 1 + 1 + 1 = 3.
b) Para calcular o conjunto de valores da expressão com a, b e c negativos, utilizando a definição de módulo, basta fazer:
= = −1 + (−1) + (−1) = −3
13. a) Do enunciado, tem-se quê f(x) = Para identificarmos o ponto em quê a função não está definida, precisa-se analisar seu domínio. Sabendo quê, para x = 3, o denominador se anula, conclui-se quê a função não está definida para esse valor.
b) Tem-se quê f(x) = , então:
14. a) Para obtêr o gráfico de f(x) = , pode-se considerar o gráfico da função f1(x) = transladado horizontalmente 3 unidades para a direita.
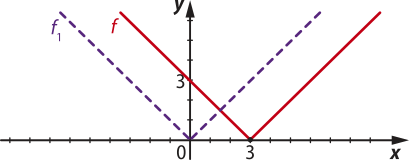
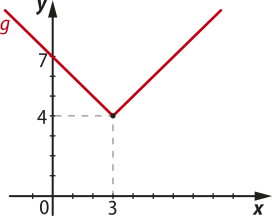
b) Para obtêr o gráfico de g(x) = + 4, pode-se considerar o gráfico da função f(x) = do item a transladado verticalmente 4 unidades para cima.
c) Pela definição de módulo, tem-se:
h (x) = | − 2x + 1| =
Calculando alguns pontos de h(x), em quê x é menor, igual e maior do quê , obtém-se:
x = 0 ⇒ −2 ⋅ 0 + 1 = 1 ⇒ (0, 1)
x = ⇒ −2 ⋅ + 1 = 0 ⇒ (, 0)
x = 1 ⇒ 2 ⋅ 1 − 1 = 1 ⇒ (1, 1)
Logo, o gráfico de h(x) é dado por:
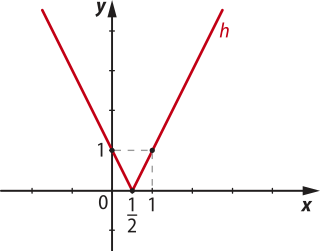
d) Para determinar o gráfico de j(x) = − 3, pode-se considerar o gráfico de h(x) = do item c e realizar uma translação vertical de 3 unidades para baixo.
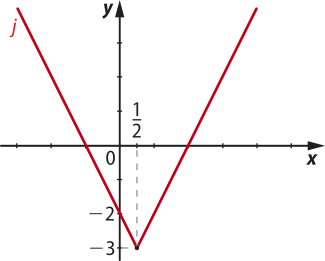
e) O gráfico da função m(x) = − 5 póde sêr obtído pela translação vertical do gráfico de m1 cinco unidades para baixo.
Pela definição de módulo, tem-se:
m1(x) = =
Os zeros das funções y1 = − x2 + 4 e y2 = x2 − 4 são x(minutos)" = −2e x(segundos)" = 2, e os vértices de suas respectivas parábolas são:
= = 0 ⇒ y1(0) = −(0)2 + 4 = 4 ⇒ V1 = (0, 4)
= = 0 ⇒ y2(0) = 02 − 4 = −4 ⇒ V2 = (0, −4)
Assim, podem sêr esboçados os gráficos de y1 e y2. A junção dêêsses dois gráficos, considerando os respectivos domínios: D(y1) = {x ∈ ℝ | −2 < x < 2} e D(y2) = {x ∈ ℝ | x ≤ −2 ou x ≥ 2}, determina a função m1(x) quê, ao sêr transladada conforme já comentado, resulta no gráfico de m(x):
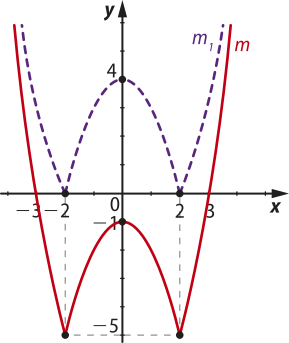
15. Analisando o gráfico, percebe-se quê ele representa uma função modular f(x) ôbitída pela translação horizontal do gráfico da função g(x) = em uma unidade para a esquerda e uma translação vertical de duas unidades para cima.
Assim, essa função póde sêr descrita por f(x) = + b, com a = 1 e b = 2, ou seja, f(x) = + 2.
Como, para qualquer valor real de x, a função está bem definida, segue quê D(f) = ℝ. Além díssu, como ≥ 0, segue quê f(x) = + 2 ≥ 2, para qualquer valor de x em seu domínio.
Dessa forma, Im(f) = {y ∈ ℝ | y ≥ 2}.
Página trezentos e sessenta e cinco
16. Para encontrar o valor de n para quê P(n) seja mínimo, considera-se:
P(n) = 8 − , com n ∈ {1, 2, 3, …, 11, 12}
Pela definição de módulo, tem-se quê:
= 6 − n, para 6 − n ≥ 0 ⇒ n ≤ 6
= −6 + n, para 6 − n < 0 ⇒ n > 6
Então, para n ≤ 6 tem-se:
P(n) = 8 − 6 + n = 2 + n (função crescente)
P(n) tem valor mínimo para n = 1, em quê P(1) = 3.
Para n > 6, tem-se:
P(n) = 8 − (−6 + n) = 14 − n (função decrescente)
P(n) tem valor mínimo para n = 12, em quê P(12) = 2.
Logo, o valor mínimo absoluto de P(n) acontece para n = 12.
17. a) Pela definição de módulo, tem-se:
=
=
Portanto, f será dada por: f(x) =
Considerando a primeira sentença, f é decrescente, e o gráfico passa pelo ponto: x = −1 ⇒ −2 ⋅ (−1) + 2 = 4 ⇒ (−1, 4).
Com bó-linha aberta em: x = 0 ⇒ −2 ⋅ 0 + 2 = 2 ⇒ (0, 2).
Considerando a segunda sentença, f é constante, e o gráfico é um segmento de reta paralelo ao eixo x e limitado pêlos pontos extremos (0, 2) e (2, 2).
Para a terceira sentença, f é crescente, e o gráfico passa pêlos pontos:
x = 2 ⇒ 2 ⋅ 2 − 2 = 2 ⇒ (2, 2)
x = 3 ⇒ 2 ⋅ 3 − 2 = 4 ⇒ (3, 4)
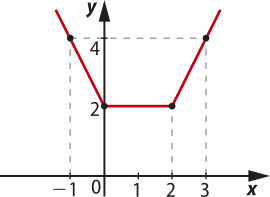
Portanto, o domínio da função é D(f) = ℝ, e a imagem é Im(f) = {y ∈ ℝ | y ≥ 2}.
b) Pela definição de módulo, tem-se:
Portanto, g será dada por: g(x) =
Considerando a primeira sentença, g é decrescente, e o gráfico passa pelo ponto: x = 0 ⇒ −2 ⋅ 0 + 4 = 4 ⇒ (0, 4)
Com bó-linha aberta em: x = 1 ⇒ −2 ⋅ 1 + 4 = 2 ⇒ (1, 2)
Considerando a segunda sentença, g é constante, e o gráfico é um segmento de reta paralelo ao eixo x e limitado pêlos pontos extremos (1, 2) e (3, 2).
Para a terceira sentença, g é crescente, e o gráfico passa pêlos pontos:
x = 3 ⇒ 2 ⋅ 3 − 4 = 2 ⇒ (3, 2)
x = 4 ⇒ 2 ⋅ 4 − 4 = 4 ⇒ (4, 4)
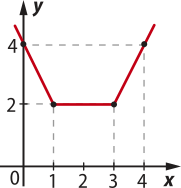
Portanto, o domínio da função é D(g) = ℝ, e a imagem é Im(g) = {y ∈ ℝ | y ≥ 2}.
18. a) Para x < 0: −(3x + 1) = 6 ⇒ x =
Para x ≥ 0: 3x + 1 = 6 ⇒ x =
Logo, S = {}.
b) Para x < 0: = 1 ⇒ x = −1
Para x ≥ 0: 1 ⇒ x = 5
Logo, S = {−1, 5}.
c) Para x < 0: −(x2 + 4x) = 12 ⇒ x2 + 4x + 12 = 0
Resolvendo a equação do 2º grau, não se obtêm raízes reais, pois (delta)" = 16 − 48 = −32.
Para x ≥ 0: x2 + 4x = 12 ⇒ x2 + 4x − 12 = 0
Resolvendo a equação do 2º grau, obtêm-se as raízes x(minutos)" = −6 e x” = 2.
Logo, S = {−6, 2}.
19. Dada a equação x2 − 5x + 6 = obtém-se: Para x < 0: x2 − 5x + 6 = −x + 3 ⇒ x2 − 4x + 3 = 0 ⇒ x = 1 ou x = 3
Para x ≥ 0: x2 − 5x + 6 = x − 3 ⇒ x2 − 6x + 9 = 0 ⇒ x = 3
Vamos verificar se as soluções encontradas são válidas.
Substituindo os valores na equação, tem-se: Para x = 3 ⇒ (3)2 − 5 ⋅ (3) + 6 = ⇒ 0 = 0 (verdadeiro)
Para x = 1 ⇒ (1)2 − 5 ⋅ (1) + 6 = ⇒ 2 = 2 (verdadeiro)
Então, a soma das raízes distintas é: 3 + 1 = 4.
Resposta: alternativa e.
20. Considerando x ≥ 0, obtém-se: x = x − 6 ⇒ 0 = 6 (absurdo).
Ao considerar x < 0, obtém-se:
−x = x − 6 ⇒ x = 3; porém, x não póde sêr igual a esse valor, pois consideramos x < 0. Portanto, a equação não tem solução.
Resposta: alternativa d.
21. Para calcular a intersecção do conjunto S1 ∩ S2, precisa-se calcular primeiro a condição de existência de (i), então:
1 − 2x ≥ 0 ⇒ x ≤
Em seguida, calcula-se o valor de x, da equação modular:
= 1 − 2x
Para x ≥ 0: x − 5 = 1 − 2x ⇒ x = 2 (não convém, pois não satisfaz a condição de existência)
Para x < 0: −(x − 5) = 1 − 2x ⇒ x = −4
S1 = {−4}
Agora, precisa-se calcular a condição de existência de (ii), então:
6 − 2x ≥ 0 ⇒ x ≤ 3
Em seguida, calcula-se o valor de x da equação modular:
= 6 − 2x
Para x ≥ 0: 2x − 6 = 6 − 2x ⇒ x = 3
Para x < 0: −(2x − 6) = 6 − 2x ⇒ 0x = 0 ⇒ 0 = 0
S2 = {x ∈ ℝ | x ≤ 3}
Portanto, S1 ∩ S2 = {−4}.
Resposta: alternativa d.
22. a) Para determinar o kilometro da rodovia em quê está localizado o posto, deve-se calcular d(x) = 0, pois é o ponto em quê a distância até o posto é nula. Assim:
d(x) = 0 ⇒ = 0 ⇒ x − 200 = 0 ⇒ x = 200
Portanto, o posto está localizado no kilometro 200 da rodovia.
b) Do enunciado, d(x) = 135, então:
Logo, a pessoa póde estar no kilometro 65 ou no 335 da rodovia.
Página trezentos e sessenta e seis
23. Dada a equação , temos quê:
x2 − 3x + 2 = 2x − 3 (I)
x2 − 3x + 2 = −(2x − 3) (II)
De (I), obtém-se a equação x2 − 5x + 5 = 0, cujas raízes são
x(minutos)" = e x” =
De (II), obtém-se a equação x2 − x − 1 = 0, cujas raízes são
x(minutos)" = e x” =
Fazendo o produto entre as raízes:
Resposta: alternativa a.
24. Dada a equação: − 4 = 0, tem-se:
− 4 = 0 ⇒ = 4
Para x ≥ 0:
x2 − 8 = 4 ⇒ x2 = 12 ⇒ x =
Para x < 0:
−(x2 − 8) = 4 ⇒ x2 = 4 ⇒ x = ±2
Portanto, o produto das raízes é:
⋅ 2 ⋅ (−2) = 48.
Resposta: alternativa e.
25. Do enunciado, obtém-se:
Das definições de módulo, obtém-se:
− 8 = −8 ⇒ x = 0
− 8 = 8 ⇒ x = ou x =
Portanto, as raízes irracionais são 4 e −4.
Resposta: alternativa c.
26. Para calcular o valor de = 1, pode-se considerar quê f(x) = 1 ou f(x) = −1.
Observando o gráfico f(x), verifica-se quê f(x) = 1 em 3 pontos e f(x) = −1 em 2 pontos.
Portanto, a equação = 1 tem 5 elemêntos em seu conjunto solução.
Resposta: alternativa b.
27. Do enunciado tem-se f(x) = e g(x) = + 1. Desse modo:
f(x) =
g(x) =
Determinando x tal quê f(x) = g(x), tem-se:
Para x < 0: 0 = x + 1 ⇒ x = −1
Para x ≥ 0: x = −x + 1 ⇒ x =
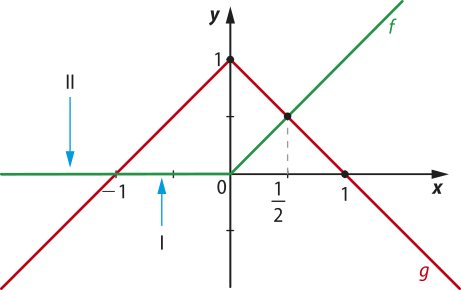
Analisando cada afirmativa, tem-se:
I. Falsa, pois, para −1 < x < 0, g(x) > f(x).
II. Falsa, pois, para x ≤ −1, f(x) ≥ g(x).
III. Falsa, pois as raízes da equação f(x) = g(x) são x(minutos)" = −1 e x” = , cuja soma é .
Dessa forma, todas as afirmativas são falsas.
Resposta: alternativa a.
28.
a) Da definição, sabe-se quê f é sobrejetora quando todo elemento do contradomínio é imagem de pelo menos um elemento do domínio da função. Portanto é apenas sobrejetora, pois não sobram elemêntos no conjunto imagem Im(f) = B. Não é injetora, pois o elemento do conjunto B é imagem de todos os elemêntos de A simultaneamente. Como a função é sobrejetora, mas não é injetora, não póde sêr bijetora.
b) Nem sobrejetora nem injetora, visto quê sobram elemêntos em B (não sobrejetora) e existe pelo menos um elemento em B quê é imagem de mais de um elemento de A simultaneamente (não injetora). Por exemplo, o elemento 4 em B é imagem de −2 e 2.
c) Da definição, sabe-se quê uma função é bijetora quando ela é sobrejetora e injetora, simultaneamente. Portanto, é bijetora, porque não sobram elemêntos em B (sobrejetora), e cada elemento em A corresponde a um único elemento em B (injetora).
d) Da definição, sabe-se quê f é injetora quando os elemêntos distintos de um conjunto são associados por f a elemêntos distintos de outro conjunto. Portanto, é apenas injetora, porque cada elemento em B corresponde a um único elemento em A. Não é sobrejetora, pois sobram elemêntos em B. Portanto, não é bijetora.
29. No item a, a função é apenas sobrejetora, uma vez quê não sobram elemêntos no contradomínio. Não é injetora, pois existem elemêntos do contradomínio quê são a imagem de mais de um elemento do domínio simultaneamente. Como a função é sobrejetora, mas não é injetora, não póde sêr bijetora.
No item b, a função é injetora, mas não é sobrejetora, visto quê o contradomínio da função é estritamente positivo. Como a função é injetora, mas não é sobrejetora, não póde sêr bijetora.
No item c, o gráfico não representa uma função, pois é possível traçar uma reta paralela ao eixo y, a qual intersecta o gráfico em mais de um ponto.
No item d, a função é bijetora, pois, para cada elemento do contradomínio, existe um elemento correspondente no domínio (sobrejetora) e não há elemêntos distintos do domínio quê possuem a mesma imagem simultaneamente no contradomínio (injetora).
Resposta: alternativa d.
30. Analisando cada afirmação, obtêm-se:
• Falso, pois existem elemêntos do contradomínio quê são a imagem de mais de um elemento do domínio simultaneamente, por exemplo, f(2) = f(3) = 2.
• Falso, pois esse intervalo corresponde ao contradomínio.
• Falso, pois f(4) = 3.
• Verdadeiro.
Resposta: alternativa a.
31. Do enunciado, tem-se quê f(x) = x2 + 2x e g(x) = 1 − 3x; então, para determinar f(g(x)), em cada item, aplica-se a definição de função composta, ou seja:
a) f(g(x)) = (1 − 3x)² + 2 ⋅ (1 − 3x)
f(g(x)) = 9x² − 12x + 3
b) g(f(x)) = 1 − 3 ⋅ (x² + 2x)
g(f(x)) = −3x2 − 6x + 1
Página trezentos e sessenta e sete
c) (f ∘ f)(x) = (x² + 2x)² + 2 ⋅ (x² + 2x)
(f ∘ f)(x) = x4 + 4x3 + 6x2 + 4x
d) (g ∘ g)(x) = 1 − 3 ⋅ (1 − 3x)
(g ∘ g)(x) = 9x − 2
32. Como f(x) = 3x + 5 e g(x) = 2x − 3, tem-se:
a) f(g(x)) = 0 ⇒ 3 ⋅ (2x −3) + 5 = 0 ⇒ x =
b) g(f(x)) = 0 ⇒ 2 ⋅ (3x + 5) − 3 = 0 ⇒ x =
33. Como f(x) = segue quê:
f(f(x)) = 1 ⇒ = 1 ⇒ x =
34. Sejam f: ℝ → ℝ tal quê f(x) = x2 − 2x − 3 e g: ℝ → ℝ tal quê g(x) = 4x + m. Sabe-se quê f(g(−1)) = 12. Para encontrar o valor de m, precisa-se calcular:
f(g(x)) = (4x + m)2 − 2 ⋅ (4x + m) − 3
f(g(x)) = 16x2 + 8xm + m2 − 8x − 2m − 3
Para f(g(−1)) = 12, tem-se
16 ⋅ (−1)2 + 8 ⋅ (−1) ⋅ m + m2 − 8 ⋅ (−1) − 2m − 3 = 12 ⇒ m2 − 10m + 21 = 12 ⇒ m2 − 10m + 9 = 0
Resolvendo a última equação, obtêm-se as raízes m’ = 1 e m” = 9.
Portanto, m = 1 ou m = 9.
35. Do enunciado, tem-se quê f(x) = , x ≠ 1, e g(x) = 2x − 4; portanto, para calcular f(g(2)) + g(f()), fazemos:
f(g(x)) =
f(g(2)) = = −1
g(f(x)) = 2 ⋅ −4 = −4
g(f()) = −4=−8
Logo:
−1 − 8 = −9
Resposta: alternativa c.
36. Como g(x) = 2x + 1 e g(f(x)) = 2x2 + 2x + 1, então:
g(f(x)) = 2 ⋅ f(x) + 1
Dessa forma, podemos escrever:
2 ⋅ f(x) + 1 = 2x2 + 2x + 1 ⇒ f(x) = x2 + x
Sendo assim:
f(7) = 72 + 7 = 56
37. a) A função f é bijetora, portanto possui invérsa. Sabe-se quê:
f(x) = x − 3 ⇒ f(x) = y ⇒ y = x − 3
Trocando x por y e y por x, obtém-se f−1 (x), então:
x = y − 3 ⇒ y = x + 3
Portanto, f−1 (x) = x + 3.
b) A função g é bijetora, portanto possui invérsa. Sabe-se quê:
g(x) = ⇒ g(x) = y ⇒ y =
Trocando x por y e y por x, obtém-se g−1 (x), então:
x = ⇒ y = 4x − 2
Portanto, g−1 (x) = 4x − 2.
38. Sejam f(x) = ax − 2 e g sua função invérsa. Sabendo quê f(−2) = 10, tem-se:
f(−2) = a ⋅ (−2) − 2 = 10 ⇒ a = −6
Dessa forma, f(x) = −6x − 2. Tomando y = −6x − 2 e trocando x por y e y por x, obtém-se f−1 (x) = g(x), então:
x = −6y − 2 ⇒ y =
Portanto, g(x) = .
39. a) Considerando y = f(x), obtém-se:
y = f(x) = ⇒ y =
Para obtêr f−1 (x), deve-se trocar x por y e y por x, ou seja:
x = ⇒ y =
Portanto, f−1 (x) = .
b) O domínio de f−1 é o conjunto de números reais tais quê seu denominador seja diferente de zero. Desse modo:
x − 2 ≠ 0 ⇒ x ≠ 2
Portanto, D(f−1) = {x ∈ ℝ | x ≠ 2}.
c) Sabendo quê f−1 (x) = , tem-se: f−1 (−3) = = 2.
40. Para resolver os itens, considere quê duas funções são inversas entre si se a reta y = x for o eixo de simetria entre seus gráficos.
a) O eixo de simetria das funções é y = −x. Portanto, elas não são inversas uma da outra.
b) O eixo de simetria das funções é y = x. Portanto, elas são inversas uma da outra.
c) O eixo de simetria das funções é o eixo x. Portanto, elas não são inversas uma da outra.
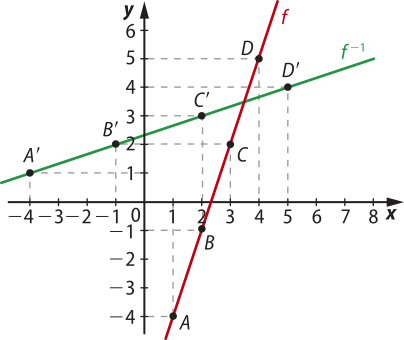
41. Para construir o gráfico da função invérsa, pode-se marcar as coordenadas dos pares ordenados:
A(1, −4); B(2, −1); C(3, 2); D(4, 5)
Como o par ordenado é da forma (x, y) e, na função invérsa, invertem-se as variáveis x e y, podem-se encontrar os novos pares ordenados quê darão origem à reta da função invérsa invertendo-se os valores de x e y:
A’(−4, 1); B’(−1, 2); C’(2, 3); D’(5, 4)
Com esses novos pontos, constrói-se o gráfico da função invérsa f−1.
Atividades complementares
1. Do enunciado, tem-se a função f(x) =
Então, sabe-se quê:
• se x ≤ −1, então f(x) é uma reta decrescente e f(−1) = 2.
• se −1 < x ≤ 2, então f(x) é uma parábola de concavidade para cima quê passa pela origem e f(2) = 8.
• se x > 2, então f(x) é uma reta constante de valor 8.
Página trezentos e sessenta e oito
Dessa forma, o gráfico quê se encaixa nessas condições é:
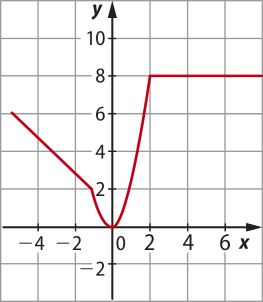
Resposta: alternativa a.
2. Note quê, para:
· x = 0, temos f(0) = −0² + 4 = 4
· x = 1, temos f(1) = −1² + 4 = 3
No intervalo ]1; 3], temos f(x) = x² − 4x + 6; então, para:
· x = 2, temos f(2) = 2² − 4 ⋅ 2 + 6 = 2
· x = 3, temos f(3) = 3² − 4 ⋅ 3 + 6 = 3
O gráfico da alternativa b é o único quê satisfaz as condições acima e representa as leis de correspondência da função f.
Resposta: alternativa b.
3. De acôr-do com a função, temos:
= 0; = 1; = 0; = 0; = 0.
Resposta: alternativa b.
4. Esboçando o gráfico dessa função, obtemos:
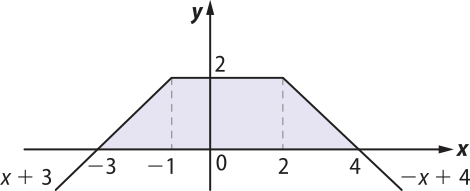
Logo, a área A da região requerida é A = = 10.
Resposta: alternativa b.
5. Do enunciado, tem-se f(x) = ⋅ 50, em quê x representa cada dia do ano. Se o lucro pretendido é R$ 5.750,00, então:
|x − 200| ⋅ 50 = 5.750 ⇒
Dessa forma, como cada mês tem cerca de 30 dias, então x = 85 ocorre durante o mês de março e x = 315 ocorre durante o mês de novembro.
Portanto, o lucro desejado será possível nos meses de março e novembro.
Resposta: alternativa c.
6. Esboçando o gráfico da função f, temos:
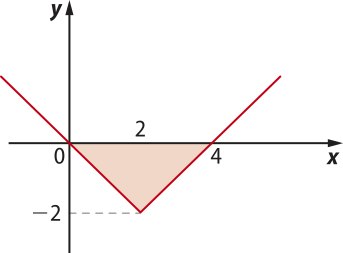
Portanto, a área S desejada é S = = 4.
Resposta: alternativa d.
7. Observe as etapas para a representação do gráfico desejado.
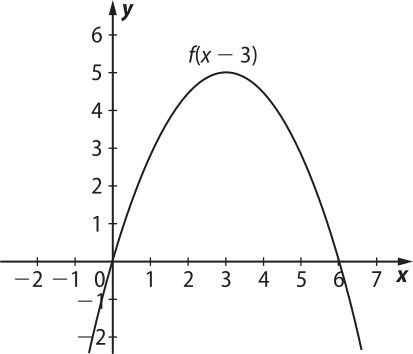
Etapa 1. Gráfico da função f(x − 3) é dado por:
Etapa 2. Gráfico da função é representado por:
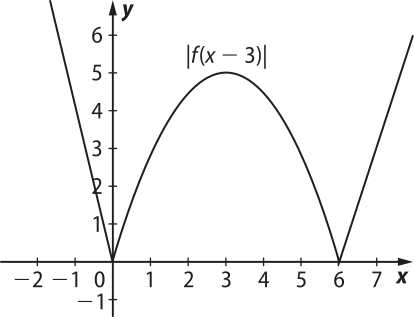
Etapa 3. Gráfico da função + 2 é dado por:

Resposta: alternativa b.
8. Ao analisar o gráfico, podem-se definir as funções:
f(x) = − 2 e g(x) = + 2.
Depois, é preciso analisar cada uma das sentenças:
• Primeira sentença
f(−1) = − 2 = − 2 = 0
g(−2) = + 2 = −1 + 2 = 1
g(f(−1)) − f(g(−2) + 2) = g(0) − f(1 + 2) = ( +2) − ( − 2) = 2 − 0 = 2 (verdadeira)
• Segunda sentença
g(−4) = + 2 = 0
f(g(−4) + 1) + 3 = f(0 + 1) + 3 = f(1) + 3 = − 2 + 3 = 1 (verdadeira)
• Terceira sentença
Ao observar o gráfico, pode-se concluir quê f(x) = − 2 (verdadeira).
Logo, as 3 afirmações são verdadeiras.
Resposta: alternativa b.
Página trezentos e sessenta e nove
9. Pela definição de módulo, tem-se quê f: [−5, 3] → A ⊂ ℝ é dada por:
f(x) = − 3 =
Assim, para −5 ≤ x < −2, f é parte de uma função afim decrescente, quê assume seu maior valor para x = −5, e decresce até um valor (que não pertence à função) de x = −2:
f(−5) = −(−5) − 5 = 0
f(−2) = −(−2) − 5 = −3
Para −2 ≤ x ≤ 3, f é parte de uma função afim crescente, cujo menor valor ocorre para x = −2 e o maior valor ocorre para x = 3:
f(−2) = −2 − 1 = −3
f(3) = 3 − 1 = 2
Como f é sobrejetora, segue quê A = Im(f) = ]−3, 0] ∪ [−3, 2].
Logo, A = [−3, 2].
Resposta: alternativa d.
10. Do enunciado, obtém-se: f(2x + 1) = 2x + 4 e g(x + 1) = 2x − 1 para todo x ∈ ℝ.
Para calcular f ∘ g(x), precisa-se, primeiro, determinar f(x); logo:
f(2x + 1) = 2x + 4
f(2x + 1) = (2x + 1) + 3
Logo, pode-se observar quê f(x) = x + 3.
De forma análoga, determina-se a função g(x):
g(x + 1) = 2x − 1
g(x + 1) = 2x + 2 − 3
g(x + 1) = 2(x + 1) − 3
Logo, pode-se observar quê g(x) = 2x − 3.
Ao fazer a função composta f(g(x)), obtém-se:
f(g(x)) = (2x − 3) + 3 = 2x
Portanto, a função f ∘ g(x) = 2x.
Resposta: alternativa d.
11. Do enunciado, tem-se quê f: [0, +∞[ → [4, +∞[, definida por f(x) = (x + 2)2 e f−1: [4, +∞[ → [0, +∞[. Para calcular a função invérsa, consideramos f(x) = y, então:
y = (x + 2)2
Realizando-se a troca de x por y e de y por x, obtém-se:
x = (y + 2)2
Isolando a variável y e sabendo quê y ≥ 0:
= (y + 2) ⇒ y = − 2. Logo, f−1 (x) = − 2
Resposta: alternativa d.
12. Do enunciado, obtém-se: f(x) = , D(f) = ℝ − {1}.
Considerando y = f(x), obtém-se:
y = f(x) = ⇒ y =
Para obtêr f−1 (x), deve-se trocar x por y e y por x, ou seja:
x = ⇒ y =
Portanto, f−1 (x) =
O domínio de f−1 é o conjunto de números reais tais quê seu denominador seja diferente de zero. Desse modo:
x − 3 ≠ 0 ⇒ x ≠ 3
Portanto, D(f−1) = {x ∈ ℝ | x ≠ 3} ou D(f−1) = ℝ − {3}.
Resposta: alternativa b.
Capítulo 4 • Função logarítmica
Atividades
1. Pela definição de logaritmos e suas consequências, obtêm-se:
a) log9 1 = x ⇔ 9x = 1 ⇒ 9x = 90 ⇒ x = 0 (definição)
b) log8 8 = x ⇔ 8x = 81 ⇒ x = 1 (definição)
c) = x ⇔ ⇒ x = 3(definição)
d) = x ⇒ x = 7 (4ª consequência)
e) = x ⇔ ⇒ x = 1 (definição)
f) = x ⇔ (3)−1x = 35 ⇒ x = −5 (definição)
2. Aplicando a definição dos logaritmos, obtêm-se:
a) = x ⇔ = 4 ⇒ = 22 ⇒ x =
b) log5 0,000064 = x ⇔ 5x = 0,000064 ⇒ 5x = ⇒ 5x = 5−6 ⇒ x = −6
c) = x ⇔ 72x = ⇒ x =
d) = x ⇔ 2x = 2−4 ⇒ x = −4
e) = x ⇔ 2−x = ⇒ x =
f) = x ⇔ 2−2x = 210 ⇒ x = −5
3. a) Considere log5 = x e = y. Pela definição, obtêm-se:
= x ⇔ 5x = 5−2 ⇒ x = −2
= y ⇔ ⇒ y = −2
= x + y = −2 + (−2) = −4
b) Considere 27 = x, log10 0,001 = y e log0,1 = z.
Pela definição, obtêm-se:
= x ⇔ 3−x = 33 ⇒ x = −3
log10 0,001 = y ⇔ 10y = 10−3 ⇒ y = −3
log0,1 = z ⇔ 10−z = ⇒ z =
+ log10 0,001 − log0,1 = x + y − z = −3 + (−3) −
4. Aplicando propriedades da potenciação e a 4ª consequência dos logaritmos, obtém-se:
m = +
m = 25 ⋅ + ⋅
m = 32 ⋅ 3 + 7 ⋅ 2 = 110
5. a) Aplicando a 2ª e a 3ª consequências, obtém-se: 1 − (−7) = 8.
b) Aplicando a 4ª consequência em cada termo, obtém-se: 27 ∶ () = 54.
c) Aplicando a 1ª e a 3ª consequências, tem-se: 05 = 0.
d) Aplicando a 1ª consequência e a definição, tem-se:
6. Considerando as informações do enunciado e aplicando a definição dos logaritmos, têm-se:
a = log10 0,001 = −3; b = =6; c = 3⋅log2 8=9
Portanto, a equação será:
−3x2 + 6x + 9 = 0
Ao resolver a equação, obtêm-se as raízes x(minutos)" = −1 e x(segundos)" = 3.
S = {−1, 3}
Página trezentos e setenta
7. Seja x o número a sêr calculado. Tem-se:
logp x = 4 ⇔ p4 = x
x = 8 ⇔ = x
Portanto: p4 = ⇒ p4 = ⇒ x = ⇒ x2 − 6.561x = 0.
Resolvendo a equação do 2º grau, obtêm-se as raízes x(minutos)" = 0 (não satisfaz a condição de existência) e x(segundos)" = 6.561.
O número é 6.561.
8. Considerando a condição de existência dos logaritmos, conclui-se quê:
a) 1 − x > 0 ⇒ x < 1
{x ∈ ℝ | x < 1}
b) 5x − 2 > 0 e x − 3 > 0
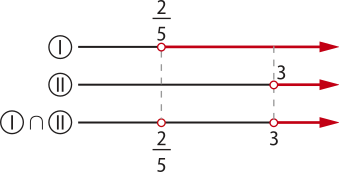
{x ∈ ℝ | x > 3}
c) x2 + 4x − 5 > 0
Resolvendo a equação x2 + 4x − 5 = 0, associada à inequação, obtêm-se as raízes x’ = −5 e x” = 1. Como o coeficiente a = 1 é maior do quê zero, a parábola descrita por x2 + 4x − 5 possui concavidade voltada para cima:

{x ∈ ℝ | x < −5 ou x > 1}
d) 50 − 5x − x2 > 0
Resolvendo a equação −x2 −5x + 50 = 0, associada à inequação, obtêm-se as raízes x’ = −10 e x” = 5. Como o coeficiente a = −1 é menor do quê zero, a parábola descrita por −x2 −5x + 50 possui concavidade voltada para baixo.

{x ∈ ℝ | −10 < x < 5}
9. Considerando log 11 = 1,041 e as propriedades dos logaritmos, obtêm-se:
a) log 110 = log (11 ⋅ 10) = log 11 + log 10 = 1,041 + 1 = 2,041
b) log 121 = log (11 ⋅ 11) = log 11 + log 11 = 1,041 + 1,041 = 2,082
c) log = log 1 − log 11 = 0 − 1,041 = −1,041
d) log = = ⋅ log11 = ⋅ 1, 041 = 1,5615
e) log 1,21 = log = log 121 − log 100 = 2,082 − 2 = 0,082
f) log 0,121 = log = log 121 − log 1.000 = 2,082 − 3 = −0,918
10. Aplicando as propriedades dos logaritmos, obtêm-se:
a) log 5 + log 200 = log (5 ⋅ 200) = log 1.000 = 3
b) log 100 + log 50 + log 10 + log 2 = log(100 ⋅ 50 ⋅ 10 ⋅ 2) = log100.000 = 5
c) log2 24 − log2 3 = = log2 23 = 3
d) log5 8 + log5 12,5 − log5 4 = log5 = log5 52 = 2
11. Aplicando as propriedades da potenciação e dos logaritmos, em cada item, obtêm-se:
a) logc ⇒ = = 3
b) logc (a3 ⋅ b2) = = = 13
12. Aplicando a propriedade dos logaritmos (mudança de base), obtém-se:
log2 3 ⋅ log3 2 = log2 3 ⋅ = ![]() = 1
= 1
13. Aplicando a propriedade dos logaritmos (mudança de base), para deixar todos os termos na base 3, obtém-se:
![]() = log3 3 = 1
= log3 3 = 1
14. Aplicando a propriedade dos logaritmos (mudança de base), para deixar todos os termos na base 5, obtém-se:
⇒ ![]() =
=
15. Antes de resolver o sistema, deve-se considerar a condição de existência dos logaritmos na segunda equação, ou seja, a > 0 e b > 0.
Da primeira equação, obtém-se: a + b = 20 ⇒ a = 20 − b (I)
Aplicando a propriedade do produto e a definição dos logaritmos na segunda equação, obtém-se:
log (a ⋅ b) = 2 ⇒ a ⋅ b = 102 ⇒ a ⋅ b = 100 (II)
Substituindo (I) em (II): (20 − b) ⋅ b = 100 ⇒ b2 − 20b + 100 = 0.
Resolvendo a equação do 2º grau, obtêm-se as raízes b(minutos)" = b(segundos)" = 10.
Substituindo em (I), temos: b = 10 ⇒ a = 20 − 10 ⇒ a = 10.
Como esses valores satisfazem à condição de existência, conclui-se quê a = 10 e b = 10.
S = {(10, 10)}
16. Aplicando as propriedades dos logaritmos (produto e quociente) no log 375, obtém-se:
log 375 = log (3 ⋅ 53) = log 3 + 3 ⋅ log 5 = y + 3 ⋅ log () = y + 3 ⋅ (log 10 − log 2) = y + 3 ⋅ (1 − x) = y + 3 − 3x
17. Para processar 64 bits, tem-se:
log 64 = log 26 = 6 ⋅ log 2 = 6 ⋅ log () = 6 ⋅ (log 10 − log 5) = 6 ⋅ (1 − 0,699) = 1,806
Será necessário 1,806 milisegundo.
18. Utilizando uma calculadora, obtêm-se:
a) log 0,7 ≃ −0,15490
b) log 0,12 ≃ −0,92082
c) log 834 ≃ 2,92117
d) log 0,00001 = −5
e) ln 25 ≃ 3,21888
f) ln 0,92 ≃ −0,08338
19. Utilizando uma calculadora, obtêm-se:
a) b = 101,88081 ≃ 76
b) b = 101,75587 ≃ 57
c) b = e6,20051 ≃ 493
d) b = e1,05082 ≃ 2,86
20. Utilizando uma calculadora, obtêm-se:
a) x = 10−0,5 ≃ 0,3162
b) x = 10−0,15 ≃ 0,7079
c) x = log 0,5 ≃ −0,3010
d) x = log 2 ≃ 0,3010
e) x = ln 10 ≃ 2,3026
f) x = ln 0,5 ≃ −0,6931
g) x = ln 0,15 ≃ −1,8971
h) x = ln 0,005 ≃ −5,2983
21. Utilizando uma calculadora, podem-se obtêr os valores a seguir:
Número (N) |
Potência de 10 |
logN |
|---|---|---|
75 |
101,875061 |
1,875061 |
643 |
102,808211 |
2,808211 |
1.320 |
103,120574 |
3,120574 |
1.000.000 |
106 |
6 |
0,00001 |
10−5 |
−5 |
0,7 |
10−0,154902 |
−0,154902 |
0,834 |
10−0,078834 |
−0,078834 |
Página trezentos e setenta e um
22. Utilizando uma calculadora, obtêm-se:
a) e1,098612289 ≃ b ⇒ b ≃ 3
b) e1,945910149 ≃ b ⇒ b ≃ 7
c) e−0,69314718 ≃ b ⇒ b ≃ 0,5
d) e−1 = b ⇒ b ≃ 0,367879
e) e0 = b ⇒ b = 1
23. Usando a calculadora para calcular In x ≃ 3,48124, tem-se x ≃ e3,48124 ⇒ x ≃ 32,5.
24. Aplicando a propriedade dos logaritmos (mudança de base), obtém-se:
log4 e = ≃ 0,7213
25. a) 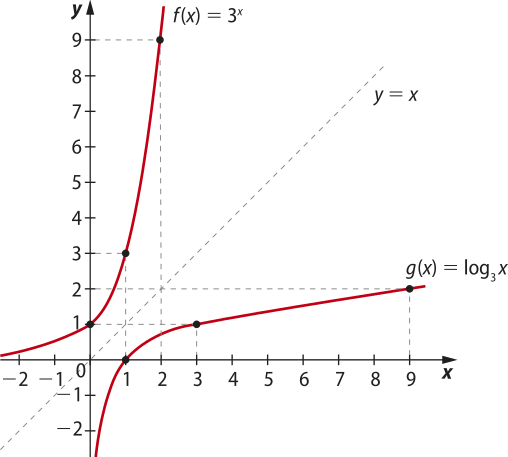
b) 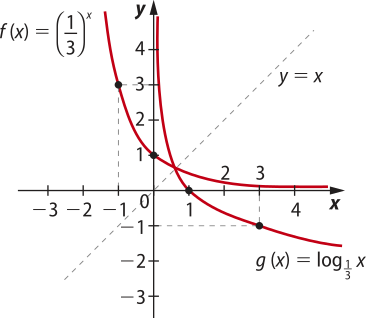
26. y = log
Como é sempre um valor positivo, o valor de x póde sêr um número real qualquer, desde quê x ≠ 0.
Portanto, a função log x, para x > 0, é simétrica à função log (−x), para x < 0, em relação ao eixo das ordenadas.
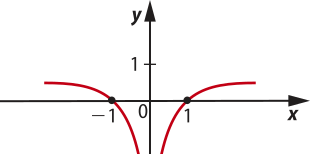
D(f) = {x ∈ ℝ | x ≠ 0}
Im(f) = ℝ
27. Para encontrar o domínio de f, deve-se analisar a função em três partes. Veja a seguir.
(I) Analisando a inequação x2 − 9 ≥ 0, obtêm-se os intervalos x ≤ −3 ou x ≥ 3, quê satisfazem à condição.

(II) x + 5 > 0 ⇒ x > −5
(III) 6 − x > 0 e 6 − x ≠ 1
x < 6 e x ≠ 5
Fazendo a intersecção entre as análises, obtêm-se:
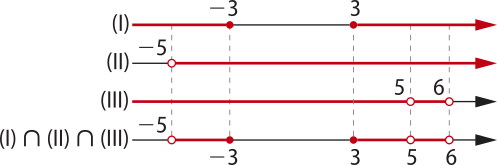
Portanto, D(f) = {x ∈ ℝ | −5 < x ≤ −3 ou 3 ≤ x < 6 e x ≠ 5}.
28. Utilizando a definição dos logaritmos, obtêm-se:
x |
f(x) = x |
g(x) = 2 + x |
|---|---|---|
2 |
4 |
|
1 |
3 |
|
1 |
0 |
2 |
4 |
−1 |
1 |
16 |
−2 |
0 |
a) 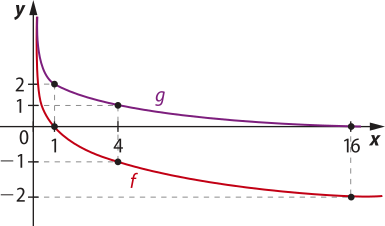
b) Para quaisquer abscissas x1 e x2 em quê x1 < x2, tem-se f(x1) > f(x2) e g(x1) > g(x2). Portanto, as funções são decrescentes.
c) O domínio de ambas as funções é o conjunto dos números reais estritamente positivos. A imagem de ambas as funções é o conjunto dos números reais, ou seja:
D(f) = e D(g) = , Im(f) = ℝ e Im(g) = ℝ
d) Espera-se quê os estudantes respondam quê a função g(x) póde sêr expressa como f(x) + 2 e quê, ao adicionarmos duas unidades à função f(x), há um deslocamento do gráfico em duas unidades na vertical para cima. Por exemplo, nesse caso, f(1) = 0 e g(1) = 2.
e) Espera-se quê os estudantes respondam quê, ao subtrairmos duas unidades na função f(x), há um deslocamento do gráfico em duas unidades na vertical para baixo.
f) Resposta pessoal. Resposta possível: Observe quê q(x) é a função f(x) com 2 adicionado à variável x. Desse modo, para obtêr o gráfico de q(x), basta considerar o gráfico de f(x) deslocado horizontalmente duas unidades para a esquerda.
29. De acôr-do com a expressão fornecida pelo enunciado, ao considerar t = 8, obtém-se:
P(8) = 105 ⋅ log3 (8 + 1) = 105 ⋅ log3 9 = 105 ⋅ 2 ⇒ P(8) = 200.000
Logo, em 8 anos, estima-se a produção de 200.000 carros.
Resposta: alternativa a.
Página trezentos e setenta e dois
30. Antes de calcular a área do triângulo, deve-se, primeiro, determinar o valor das ordenadas dos pontos C e B. Assim:
yC = log3 3 = 1
yB = log3 27 = log3 33 = 3
Portanto, a área do triângulo ABC, em u.a., é dada por:
S = = 24
Resposta: alternativa b.
31. a) Considerando a fórmula fornecida pelo enunciado e a aproximação para log 2, obtém-se:
pH = −log[H+] ⇒ pH = −log [6,4 ⋅ 10−7] ⇒ pH = −log[64 ⋅ 10−8] ⇒ pH = −(log 64 + log 10−8) ⇒ pH = −(6 ⋅ log 2 − 8 ⋅ log 10) ⇒ pH ≃ −(6 ⋅ 0,3 − 8) ⇒ pH ≃ 6,2
b) Como o pH é aproximadamente 6,2, conclui-se quê a solução é ácida.
32. a) Para encontrar o valor numérico em cada caso, deve-se substituir o valor da abscissa em cada função. Logo:
f() = 2 log2 ( −1) = 2 log2 = −2
f(2) = 2log2 (2 − 1) = 2log2 1 = 0
f(3) = 2log2 (3 − 1) = 2log2 2 = 2
g(−4) = log2 (1 − ) = log2 2 = 1
g(0) = log2 (1 − ) = log2 1 = 0
g(2) = log2 (1 − ) = log2 = −1
b) Para f(x) = g(x), tem-se:
2 log2 (x − 1) = log2 (1 − ) ⇒ log(x − 1)2 = log2 (1 − ) ⇒ (x − 1)2 = (1 − ) ⇒ x ⋅ (4x − 7) = 0
Resolvendo a equação produto, obtêm-se as raízes x(minutos)" = 0 e x’ = .
Como a resposta deve pertencer ao intervalo 1 < x < 4, então x = .
c) 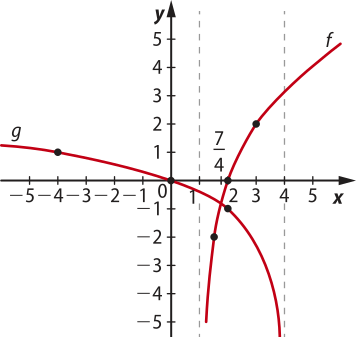
33. a) Aplicando as propriedades da potenciação, obtém-se:
f(x) = 101 + x 101 ‒ x ⇒ f(x) = 10 ⋅ 10x +
Substituindo x por log (2 + ), tem-se:
f(log10 (2 + )) = 10 ⋅ + ⇒ f(log (2 + )) = 10 ⋅ (2 + ) +
Racionalizando a segunda parcela da função, temos:
= 10 ⋅ (2 − )
Dessa forma, conclui-se quê:
f(log10 (2 + )) = 10 ⋅ (2 + ) + 10 ⋅ (2 − ) = 40.
b) Considere f(x) = 52, ou seja, 10 ⋅ 10x + = 52.
Substituindo 10x por y, temos:
10 ⋅ y + = 52 ⇒ 10y2 − 52y + 10 = 0
Resolvendo a equação, obtêm-se as raízes y(minutos)" = 5 e y(segundos)" = .
Para y(minutos)" = 5, tem-se:
10x = 5 ⇒ x = log 5 ⇒ x = log () ⇒ x = log 10 − log 2 ≃ 0,7
Para y(segundos)" = , tem-se:
10x = ⇒ x = log ⇒ x = log() ⇒ x = log 2 − log 10 ≃ −0,7
S = {−0,7; 0,7}
34. Aplicando o log7 em ambos os membros da equação exponencial, obtém-se:
7x = 4,2 ⇒ x = log7 4,2 ⇒x = ⇒ x = ≃ 0, 7374 ≃ 0, 74
Portanto, x ≃ 0,74.
35. a) A condição de existência da equação é: x > 0.
Passando log8 x para base 2, tem-se:
logx = 8
Assim, (log2 x)2 − 9 log8 x = 4 ⇒ (log2 x)2 − 3 log2 x − 4 = 0.
Fazendo log2 x = y:
y2 − 3y − 4 = 0
Resolvendo a equação, obtêm-se as raízes y(minutos)" = 4 e y(segundos)" = −1.
Substituindo os valores encontrados, tem-se:
y = 4 ⇒ log2 x = 4 ⇒ x = 16
y = −1 ⇒ log2 x = −1 ⇒ x =
Logo, S = {, 16}.
b) A condição de existência da equação é: x > 0.
(log2 x)2 + 4 ⋅ log2 x − 32 = 0
Fazendo log2 x = y:
y2 + 4y − 32 = 0
Resolvendo a equação, obtêm-se as raízes y(minutos)" = 4 e y(segundos)" = −8.
Substituindo os valores encontrados, tem-se:
y = 4 ⇒ log2 x = 4 ⇒ x = 16
y = −8 ⇒ log2 x = −8 ⇒ x =
S ={, 16}
36. Considerando os dados fornecidos e aplicando o logaritmo em ambos os lados da equação, obtém-se:
36x = 24 ⇒ log 36x = log 24 ⇒ 2x ⋅ log 6 = 3 ⋅ log 2 + log 3 ⇒ 2x ⋅ (log 2 + log 3) = 3 ⋅ log 2 + log 3 ⇒ 2x ⋅ (0,78) = 1,38 ⇒ x =
37. Considerando os dados fornecidos no enunciado, tem-se:
vmáx = 3.400 ⋅ log2 (x + 1) ⇒ 27.200 = 3.400 ⋅ log2 (x + 1) ⇒ log2 (x + 1) = 8 ⇒ x + 1 = 28 ⇒ x = 255
38. N = 3N0 ⇒ 3N0 = N0 ⋅ e0,05t ⇒ e0,05t = 3 ⇒ In e0,05t = In 3 ⇒ 0,05t ≃ 1,099 ⇒ t ≃ 21,98
O tempo será de aproximadamente 22 minutos.
Página trezentos e setenta e três
39. Resposta pessoal. Exemplo de situação-problema: Determinado bem deprecia 10% ao ano. Considerando essa informação, depois de quanto tempo o valor atualizado dêêsse bem será a mêtáde do valor de compra?
Considerando 2V = V0, tem-se:
V = V0 ⋅ (1 − i)t ⇒ V0 = 2V0 ⋅ (1 − 0,1)t ⇒ 1 = 2(0,9)t ⇒ log1 = log2(0,9)t ⇒ 0 = log2 + log(0,9)t ⇒ −log2 = log(0,9)t ⇒ t = ≃ 6,6
Aproximadamente 6,6 anos.
40. Resposta pessoal. Exemplo de situação-problema: Em 2020, o estado de Oaxaca, no México, foi atingido por um terremoto de 7,5 na escala rícher. Qual foi a energia liberada por esse terremoto? Sabendo-se quê E0 = 7 ⋅ 10−3 kW/h e quê o terremoto atingiu aproximadamente 7,5 na escala, para obtêr a energia liberada E, pode-se utilizar a fórmula:
I = ⋅ log () ⇒ 7, 5 = ⋅ log () ⇒ 11,25 = log () ⇒ 1011,25 = ⇒ E = 7 ⋅ 1011,25 −3 ≃ 109
Portanto, a energia liberada pelo terremoto de 7,5 na escala rícher foi de, aproximadamente, 109 kW/h.
41. Sabendo quê a meia-vida do césio-137 é 30 anos, pode-se utilizar a expressão fornecida pelo enunciado para determinar uma aproximação para a constante k:
M(t) = A ⋅ (2,7)kt ⇒ A = A ⋅ (2,7)30k ⇒ 1 = 2 ⋅ (2,7)30k ⇒ log 1 = log (2 ⋅ (2,7)30k) ⇒ 0 = log 2 + 30k ⋅ log 2,7 ⇒ k ≃
Para determinar o tempo em quê a quantidade de massa se torna 10% de seu valor inicial, calcula-se:
0,1A ≃ A ⋅ ⇒ log 1 ≃ log (10 ⋅ ) ⇒ 0 ≃ log10 − ⋅ log2,7 ⇒ t ≃ 100
Logo, são necessários, aproximadamente, 100 anos.
Resposta: alternativa e.
42. a) (I) A condição de existência é a2 − 2a + 1 > 0.
Considerando a2 − 2a + 1 = 0, obtém-se as raízes a’ = a” = 1.
Portanto, {a ∈ ℝ | a ≠ 1}.
(II) Aplicando a definição dos logaritmos:
log10 a2 − 2a + 1 < 2 ⇒ a2 − 2a + 1 < 102 ⇒ a2 − 2a − 99 < 0.
Considerando a2 − 2a − 99 = 0, obtêm-se as raízes a’ = −9 e a(segundos)" = 11.

Portanto, temos a2 − 2a − 99 < 0 para −9 < a < 11.
Calculando a intersecção entre (I) e (II), obtém-se:
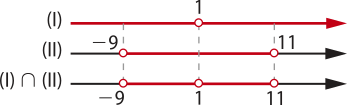
S = {a ∈ ℝ | −9 < a < 11 e a ≠ 1}
b) (I) A condição de existência é x2 + 4x − 5 > 0.
Considerando x2 + 4x − 5 = 0, obtêm-se as raízes x(minutos)" = 1 e x(segundos)" = −5.

Portanto, x < −5 ou x > 1.
(II) Aplicando a definição dos logaritmos e considerando sua base menor do quê 1:
+ 4x − 5 ≥ −4 ⇒ x2 + 4x − 5 ≤ ⇒ x2 + 4x − 21 ≤ 0
Considerando x2 + 4x − 21 = 0, obtêm-se x(minutos)" = 3 e x(segundos)" = −7.

Portanto, −7 ≤ x ≤ 3.
Calculando a intersecção entre (I) e (II), obtém-se:
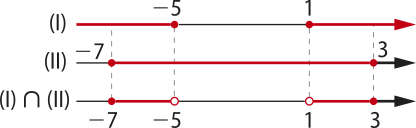
S = {x ∈ ℝ | −7 ≤ x < −5 ou 1 < x ≤ 3}
43. Considerando as informações do enunciado, tem-se:
< Q0 (0,64)t < ⇒ < (0,64)t < ⇒ log() < log(0,64)t < log() ⇒ −2 ⋅ log2 < t ⋅ log() < −log2 ⇒ −2 ⋅ log2 < t ⋅ (6 ⋅ log2 − 2) < −log2
Considerando as aproximações obtidas em uma calculadora científica:
−2 ⋅ log2 < t ⋅ (6 ⋅ log2 − 2) < −log2 ⇒ −0,602 < −0,194t < −0,301 ⇒ 0,301 < 0,194t < 0,602 ⇒ 1,55 < t < 3,1
Atividades complementares
1. Para determinar a profundidade em quê a intensidade da luz é 32% da intensidade na superfícíe, calcula-se:
I = I0 ⋅ ⇒ 0,32I0 = I0 ⋅ ⇒ 0,32 = ⇒ log 0,32 = ⇒ log = ⋅ log ⇒ 5 ⋅ log2 − 2 ⋅ log10 = ⋅ (3 ⋅ log2 − log10) ⇒ 5 ⋅ 0,3 − 2 ⋅ 1 = ⋅ (3 ⋅ 0,3 − 1) ⇒ h = 200
Logo, a profundidade será de 200 cm ou 2 m.
Resposta: alternativa c.
2. Aplicando as propriedades dos logaritmos, obtém-se:
2 log9 x + log3 6 − 6 log9 = log9 x2 + log9 36 − log9 y3 = log9
Resposta: alternativa a.
3. Aplicando as propriedades dos logaritmos, obtém-se: log5 18 =
Resposta: alternativa a.
Página trezentos e setenta e quatro
4. Sabe-se quê pH = −log[H+] e [H+] = 5,4 ⋅ 10−8 mol/L. Então, aplicando as propriedades dos logaritmos, tem-se quê: pH = −log[5,4 ⋅ 10−8] = −log(5,4) − log(10−8) = −log(54) + log 10 + 8 = −log(33 ⋅ 2) + 1 + 8 ⇒ pH = −3 log 3 − log 2 + 9
Substituindo as aproximações de log 2 e log 3, obtém-se: pH = −3 log 3 − log 2 + 9 ≃ −3 ⋅ (0,48) − 0,3 + 9 ⇒ pH ≃ 7,26
Resposta: alternativa a.
5. Determinando a condição de existência da função f(x) = logx − 1 (x² + 1), obtém-se:
x − 1 > 0 ⇒ x > 1
x − 1 ≠ 1 ⇒ x ≠ 2
Como x² + 1 > 0 para qualquer valor real de x, conclui-se quê as condições de existência, ou domínio, de f são x > 1 e x ≠ 2.
Resposta: alternativa e.
6. Pelas informações, tem-se quê h(2) = 10. Substituindo esses valores na função h, obtém-se a equação 10 = 50 ⋅ (1 − 10−2k).
Resolvendo essa equação exponencial, encontra-se:
k = ⋅ log().
Os eucaliptos serão cortados quando estiverem com 8 anos.
Logo, devemos calcular h(8):
h(8) = 50 ⋅ [1 − ] = 50 ⋅ [1 − ] = 50 ⋅ (1 − ) = 29,52
Portanto, 29,52 metros de altura.
7. Como se trata de uma equação produto com três fatores, então, para encontrar as raízes, basta igualar cada um dêêsses fatores a zero. Logo:
x + 3 = 0 ⇒ x = −3
= 0 ⇒ ∄ x ∈ ℝ
Aplicando a definição em log = 0, obtém-se:
= 100 ⇒ = 1
Para x2 + x − 1 < 0, tem-se:
x2 + x − 1 = −1 ⇒ x2 + x = 0
Resolvendo a equação do 2º grau, obtêm-se as raízes x(minutos)" = 0 e x(segundos)" = −1.
Para x2 + x − 1 ≥ 0, tem-se:
x2 + x − 1 = 1 ⇒ x2 + x − 2 = 0
Resolvendo a equação do 2º grau, obtêm-se as raízes x(minutos)" = 1 e x(segundos)" = −2.
Logo, as raízes são: −3, −2, −1, 0 e 1, ou seja, cinco raízes reais distintas.
Resposta: alternativa e.
8. Para calcular o tempo necessário para quê 2.500 pessoas sêjam atingidas por uma epidemia, deve-se considerar quê
N(t) = 2.500. Logo:
N(t) = ⇒2.500 = ⇒ 1 + 8 ⋅ 4−2t = 4 ⇒ 23−4t = 3 ⇒ log23−4t = log3 ⇒ 3 − 4t = ⇒ −4t = −1,4 ⇒ t = 0,35
Considerando quê o mês tem 30 dias, t = 0,35 equivale a 0,35 ⋅ 30 = 10,5, isto é, aproximadamente 10 dias.
Resposta: alternativa a.
9. Considerando a definição de módulo, conclui-se quê:
≤ 1 ⇒ −1 ≤ log3 (3x) ≤ 1
Aplicando a definição dos logaritmos, obtém-se:
−1 ≤ log3 (3x) ≤ 1 ⇒ ≤ 3x ≤ 3 ⇒ ≤ x ≤ 1
Logo, S = [, 1].
Resposta: alternativa c.
10. As condições de existência do logaritmo são x > 0, x ≠ 1 e x + 6 > 0. Assim, pode-se considerar quê x deve sêr um valor positivo, porém diferente de 1.
Aplicando a definição de logaritmos, obtém-se:
logx (x + 6) = 2 ⇒ x + 6 = x2 ⇒ x2 − x − 6 = 0
Resolvendo a equação do 2º grau, obtêm-se as raízes x(minutos)" = 3 e x(segundos)"= −2.
Como, pela condição de existência, x > 0, deve-se desconsiderar a solução −2. Portanto, a solução é x = 3, ou seja, um número primo.
Resposta: alternativa a.
11. Para quê a função f(x) = log10 ((x2 − x + 1)) seja definida, deve-se considerar:
x2 − x + 1 > 0 I
(x2 − x + 1) > 0 II
I x2 − x + 1 > 0
Considerando a função y = x2 − x + 1, tem-se (delta)" = 1 − 4 = −3; logo, a função não possui raízes reais e sempre assumirá um valor positivo, pois a > 0.

II (x2 − x + 1) > 0
Aplicando a definição dos logaritmos, obtém-se:
(x2 − x + 1) > ⇒ x2 − x + 1 < 1 ⇒ x2 − x < 0
Considerando x2 − x = 0, obtêm-se as raízes x(minutos)" = 0 e x(segundos)" = 1.

Portanto, 0 < x < 1.
De I ∩ II, obtém-se 0 < x < 1.
Assim, D(f) = {x ∈ ℝ; 0 < x < 1}.
Resposta: alternativa a.
12. Considerando o enunciado, é necessário quê P < 0,75V. Logo:
V = P ⋅ (1 + i)n ⇒ P < 0,75P ⋅ (1 + i)n ⇒ 1 < 0,75 ⋅ (1 + 0,0132)n ⇒ < 1,0132n
Como a aproximação fornecida está na base e, deve-se aplicar o ln em ambos os membros da inequação, assim:
ln () < ln (1,0132n) ⇒ n ⋅ 0,0131 > 0,2877 ⇒ n > 21,96
Como n é um número natural, pois representa uma parcela, pode-se considerar n = 22.
Assim, a parcela a sêr paga com a 30ª parcela será a de número 30 + 22 = 52, ou seja, a 52ª parcela.
Resposta: alternativa c.
13. Para calcular o número de parcelas cujo valor não comprometa o orçamento da pessoa, deve-se considerar P ≤ 400. Logo:
P = ⇒ ≤ 400 ⇒ 65 ⋅ 1,013n ≤ 400 ⋅ (1,013n − 1) ⇒ 65 ⋅ 1,013n ≤ 400 ⋅ 1,013n − 400 ⇒ 335 ⋅ 1,013n ≥ 400 ⇒ 1,013n ≥
Aplicando o log em ambos os membros da inequação, obtém-se: log (1,013n) ≥ log () ⇒ n ⋅ log 1,013 ≥ log 400 − log 335 ⇒ 0,005n ≥ 2,602 − 2,525 ⇒ n ≥ ⇒ n ≥ 15,4
Assim, o menor número de parcelas será 16.
Resposta: alternativa d.
Página trezentos e setenta e cinco
14. Considerando a intensidade do ronco mais alto, tem-se: 93 = 120 + 10 ⋅ log I ⇒ −2,7 = log I ⇒ I = 10−2,7.
Considerando a intensidade do ronco moderado, tem-se: 50 = 120 + 10 ⋅ log I ⇒ −7 = log I ⇒ I = 10−7.
Assim, a razão entre as duas intensidades é: = 10−2,7 − (−7) = 104,3.
Ou seja, um número entre 10.000 e 100.000.
Resposta: alternativa d.
Capítulo 5 • Razões trigonométricas na circunferência
Atividades
1. Em cada um dos itens, aplica-se a regra de três simples para calcular o quê é solicitado.
a) ![]()
⇒ x = rad
b) ![]()
⇒ x = rad
c) ![]()
⇒ x = 200°
d) ![]()
⇒ x = 9°
2. Considerando os dados fornecidos pelo enunciado, obtêm-se: raio = = 16 cm
C = 2(pi)"r = 2(pi)" ⋅ 16 cm = 32(pi)" cm Como o arco méde 8 cm, então:

⇒ x = rad
Logo, o arco de 8 cm equivale a rad ou 0,5 rad.
3. Como o relógio analógico está dividido em 12 partes iguais, cada parte méde 30°, pois 360 ∶ 12 = 30, ou seja, a cada 5 minutos, o ponteiro percórre um arco de 30°.
Então, em 25 minutos, o ponteiro percórre um arco de 150°, pois 30 ⋅ 5 = 150.
Convertendo em radiano, obtém-se:

⇒ x = rad
• Resposta pessoal. Uma possibilidade é observar uma volta completa no relógio. Uma volta completa equivale a 360° e corresponde a 60 minutos.
Então, cada minuto equivale a 6°, pois 360 ∶ 60 = 6.
Logo, 25 minutos equivalem a 150°, pois 25 ⋅ 6 = 150.
4. Observe quê é possível dividir o caminho em 3 partes.
Na primeira, de P a C, tem-se uma semicircunferência de diâmetro igual a 4 m e, portanto, raio igual a 2 m.
Desse modo, seu comprimento será:
C = = 2(pi)" m
Na segunda parte, de C a T, obtém-se novamente uma semicircunferência de raio igual a 2 m. Seu comprimento será igual ao calculado anteriormente, C = 2(pi)" m.
Na terceira parte, de T a Q, obtém-se um quarto de circunferência de raio igual a 4 m. Seu comprimento será:
C = = 2(pi)" m
Adicionando os resultados obtidos, tem-se 6(pi)" metros, quê devem sêr percorridos para ir de P a Q, seguindo as flechas.
5. a) 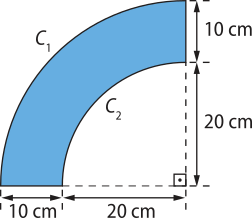
Observe quê a figura representa a quarta parte de duas circunferências concêntricas cuja diferença entre seus raios é 10 cm, pois o raio r da circunferência menor é 20 cm e o raio R da circunferência maior é 30 cm. Assim, o comprimento de cada contôrno curvo da imagem, em cm, é dado por:
C1 = = 47,1
C2 = = 31,4
Logo, o comprimento de todo o contôrno da figura, em cm, é:
47,1 + 31,4 + 10 + 10 = 98,5
b) 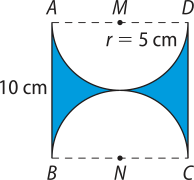
Observe quê a figura representa uma região quadrada da qual foram retiradas duas semicircunferências de mesmo raio.
Desse modo, o contôrno curvo da figura, em cm, é dado pelo comprimento de uma circunferência de raio 5 cm:
C = 2(pi)"r = 2 ⋅ 3,14 ⋅ 5 = 31,4
Logo, o comprimento de todo o contôrno da figura, em cm, é:
31,4 + 10 + 10 = 51,4
6. Observe quê a figura representa o comprimento de um arco de 20°.
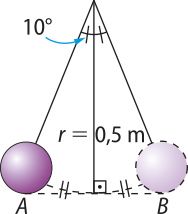
Convertendo 20° em radiano, obtém-se:
⇒ x = rad
Portanto, o comprimento do arco em m, é:
(éli)" = (alfa)" ⋅ r = ⋅ 0,5 =
7. A distância total percorrida pela primeira formiga é mêtáde do comprimento de uma circunferência de raio R:
= (pi)"R
A distância total percorrida pela segunda formiga é mêtáde do comprimento de uma circunferência de raio r mais a distância do segmento e ou seja, 1 cm para cada segmento. Logo:
+ 2 = (pi)"r + 2
A diferença entre as distâncias percorridas pelas formigas é:
((pi)"R) − ((pi)"r + 2) ⇒ (pi)"R − (pi)"r − 2 ⇒ (pi)"(R − r) − 2
Como a diferença (R − r) é 1 cm, então conclui-se quê a diferença entre os caminhos das formigas, em cm, é (pi)" − 2.
Resposta: alternativa d.
8. a) equivale a:
Logo, ao representar 36° na circunferência trigonométrica, no sentido anti-horário, obtém-se:
b) equivale a:
Logo, ao representar 135° na circunferência trigonométrica, no sentido anti-horário, obtém-se:
Página trezentos e setenta e seis
c) equivale a:
= −100°
Logo, ao representar −100° na circunferência trigonométrica, no sentido horário, obtém-se:

d) −5(pi)" equivale a:
−5(pi)" = −5 ⋅ 180° = −900°
Como −900° corresponde a duas voltas inteiras na circunferência (2 ⋅ 360° = 720°) e mais meia-volta (180°) no sentido horário, ao representar −180° na circunferência trigonométrica, obtém-se:
9. a) Analisando o arco percebe-se quê a primeira determinação positiva é 63°. Logo, os arcos kôn-gru-us a ele são dados por:
(alfa)" = 63° + k ⋅ 360°, com k ∈ ℤ
b) Analisando o arco , percebe-se quê a primeira determinação positiva é . Logo, os arcos kôn-gru-us a ele são dados por:
(alfa)" = + k ⋅ 2(pi)", com k ∈ ℤ
10. Sabe-se quê equivale a 210° e equivale a 210°.
Logo, eles são pontos coincidentes na circunferência.
• Resposta pessoal. Uma possibilidade seria adicionar uma volta completa no sentido anti-horário ao ponto de extremidade , ou seja, tomar + 2(pi)" e observar quê esta operação resulta em , concluindo quê estes pontos coincidem na circunferência.
11. a) Com relação ao ângulo 1.490°, pode-se escrever quê:
1.490° = 50° + (4 ⋅ 360°)
Com relação ao ângulo −1.030°, pode-se escrever quê:
−1.030° = 50° − (3 ⋅ 360°)
Como a primeira determinação positiva dos arcos é 50°, então eles são kôn-gru-us.
b) Com relação ao ângulo rad, pode-se escrever quê:
+ 2 ⋅ 2(pi)"
Com relação ao ângulo rad, pode-se escrever quê:
+ 3 ⋅ 2(pi)"
Como rad e rad não são arcos kôn-gru-us na primeira determinação positiva, então os ângulos rad e rad também não são kôn-gru-us.
12. a) Ao dividir −1.640° por 360°, obtém-se −4 e résto −200°.
Como 360° − 200° = 160°, pode-se afirmar quê −1.640° e 160° são kôn-gru-us e estão no segundo quadrante.
b) Ao dividir por 2(pi)", obtém-se 310 e résto .
Portanto, e são kôn-gru-us e estão no quarto quadrante.
13. a) Com relação ao ângulo 1.810°, pode-se escrever:
1.810° = 10° + (5 ⋅ 360°)
Então, o móvel dá 5 voltas completas e para no primeiro quadrante.
b) Com relação ao ângulo pode-se escrever:
+ 3 ⋅ 2(pi)"
Então, o móvel dá 3 voltas completas e para no primeiro quadrante.
c) Com relação ao ângulo −1.200°, pode-se escrever:
−1.200° = −120° − 3 ⋅ 360°
Como 360° − 120° = 240°, pode-se afirmar quê −1.200° e 240° são kôn-gru-us. Então, o móvel dá 3 voltas completas em sentido horário e para em 240°, ou seja, no terceiro quadrante.
d) Com relação ao ângulo 900°, pode-se escrever:
900° = 180° + 2 ⋅ 360°
Então, o móvel dá 2 voltas completas e para em 180°, ou seja, sobre o eixo x no ponto (−1, 0).
e) Com relação ao ângulo , pode-se escrever quê:
+ 2 ⋅ 2(pi)"
Então, o móvel dá 2 voltas completas e para no terceiro quadrante.
f) Com relação ao ângulo , pode-se escrever quê:
+ 2 ⋅ 2(pi)"
Então, o móvel dá 2 voltas completas e para em , ou seja, sobre o eixo y no ponto (0, 1).
14. Primeiro, deve-se verificar quantas voltas completas o corpo descreve:
600° = 240° + 360°
Portanto, descreve uma volta completa e um arco de 240°.
Uma volta completa equivale a:
C = 2(pi)"r ⇒ C ≃ 2 ⋅ 3,14 ⋅ 10 = 62,8
Com relação ao arco, conclui-se quê:
x = ![]() = (pi)"r
= (pi)"r
x ≃ ⋅ 3,14 ⋅ 10 ≃ 41,87
Portanto, a distância percorrida será, aproximadamente:
41,87 cm + 62,80 cm = 104,67 cm.
15. 
Inicialmente, determina-se a medida do arco

⇒ x = rad
Desse modo, segue quê:
med() = 60° = rad
med() = 60° + 90° = 150° = rad
med() = 150° + 90° = 240° = rad
med() = 240° + 90° = 330° = rad
16. I. Sentença falsa. Se esta afirmação fosse verdadeira, o arco de 120° seria côngruo ao arco de 60°, o quê não é verdade.
II. Sentença falsa. Como 1.140° = 60° + 3 ⋅ 360°, segue quê o primeiro arco não negativo côngruo a 1.140° é o arco de 60°.
III. Sentença verdadeira.
Como 180° = (pi)" rad, segue quê:
60° = rad
IV. Sentença verdadeira.
Como (pi)" rad = 180°, segue quê:
rad = = 315°
V. Sentença verdadeira. Como 45° é a primeira determinação positiva do arco, segue quê os arcos congruentes a ele serão da forma:
(alfa)" = 45° + k ⋅ 360°, com k ∈ ℤ
Resposta: alternativa d.
Página trezentos e setenta e sete
17. Calculando as medidas das extremidades dos arcos, encontram-se as seguintes representações:
a) Para k = 0 e k = 1:
b) Para k = 0, k = 1, k = 2 e k = 3:
c) Para k = 0, k = 1, k = 2 e k = 3:

18. Fazendo a redução ao primeiro quadrante de cada item, obtêm-se:
a) sen 150° = sen (180° − 30°) = sen 30° =
b) cos 150° = cos (180° − 30°) = −cos 30° =
c) sen 240° = sen (180° + 60°) = −sen 60° =
d) cos 240° = cos (180° + 60°) = −cos 60° =
e) sen 315° + cos 315° = sen (360° − 45°) + cos (360° − 45°) = −sen 45° + cos 45° = = 0
19. a) 135° é um arco do 2º quadrante pois 90° < 135° < 180°. Logo:
sen 135° = sen (180° − 45°) = sen 45° =
cos 135° = cos (180° − 45°) = −cos 45° =
b) é um arco do 2º quadrante, pois < < (pi)". Logo:
sen = sen((pi)" − ) = sen =
cos = cos ((pi)" − ) = −cos =
c) possui sua 1ª determinação positiva em cujo arco pertence ao 2º quadrante, pois < < (pi)".
Logo: sen = sen ((pi)" − ) = sen =
cos = cos ((pi)" − ) = −cos =
d) −240° possui sua 1ª determinação positiva em 120°, cujo arco pertence ao 2º quadrante, pois 90° < 120° < 180°.
Logo: sen (−240°) = sen 120° = sen (180° − 60°) = sen 60° =
cos (−240°) = cos 120° = cos (180° − 60°) = −cos 60° = −
20. Para determinar as coordenadas de P, é necessário calcular o seno e o cosseno de 120°, uma vez quê P(cos 120°, sen 120°). Assim:
sen 120° = sen (180° − 60°) = sen 60° =
cos 120° = cos (180° − 60°) = −cos 60° =
Portanto, as coordenadas de P são dadas por ().
Resposta: alternativa a.
21. a) Considerando a expressão sen 360° + sen 540° − 4 sen 1.710°, tem-se: sen 360°= 0
sen 540°= sen 180° = 0
sen 1.710° = sen 270° = −1
Ao substituir na expressão, obtém-se:
0 + 0 − 4 ⋅ (−1) = 4
b) Considerando a expressão cos 810° + 4 cos 3.780° cos 1.350°, tem-se: cos 810° = cos 90° = 0
cos 3.780° = cos 180° = −1
cos 1.350°= cos 270° = 0
Ao substituir na expressão, obtém-se:
0 + 4 ⋅ (−1) ⋅ (0) = −4.
22. Para julgar cada item a seguir, pode-se converter o ângulo quê está em radiano em grau e, a partir daí, verificar em qual quadrante ele está.
a) Verdadeiro.
![]() ⇒ ⇒ x ≃ 458,6°
⇒ ⇒ x ≃ 458,6°
x ≃ 458,6° − 360° = 98,6°
Como x está localizado no 2º quadrante, conclui-se quê sen x > 0.
b) Verdadeiro.
![]() ⇒ ⇒ x ≃ 573,2°
⇒ ⇒ x ≃ 573,2°
x ≃ 573,2° − 360° = 213,2°
Como x está localizado no 3º quadrante, conclui-se quê cos x < 0.
c) Falso.
![]() ⇒ ⇒ x ≃ 286,6°
⇒ ⇒ x ≃ 286,6°
Como x está localizado no 4º quadrante, conclui-se quê sen x < 0.
• Resposta pessoal. Uma possibilidade seria o estudante analisar o sinal do seno e o do cosseno com base na informação de quê uma volta completa na circunferência corresponde a um arco de 2(pi)" rad. Desse modo, por exemplo, rad < 5 rad < 2(pi)" rad, segue quê sen 5 tem extremidade sobre o 4º quadrante e, portanto, sen 5 < 0.
23. a) Pelos arcos kôn-gru-us, sabe-se quê:
9(pi)" = (pi)" + 4 ⋅ 2(pi)" ⇒ sen (9(pi)" − (alfa)") = sen ((pi)" − (alfa)") = sen (alfa)"
5(pi)" = (pi)" + 2 ⋅ 2(pi)" ⇒ sen (5(pi)" − (alfa)") = sen ((pi)" − (alfa)") = sen (alfa)"
Desse modo, tem-se: sen (9(pi)" − (alfa)") + sen (5(pi)" − (alfa)") = sen (alfa)" + sen (alfa)" = 2sen (alfa)"
b) Pelos arcos kôn-gru-us, sabe-se quê:
−900° = 180° − 3 ⋅ 360° ⇒ sen ((alfa)" − 900°) = sen (180° + (alfa)") = −sen (alfa)"
−540° = 180° − 2 ⋅ 360° ⇒ cos ((alfa)" − 540°) = cos (180° + (alfa)") = −cos (alfa)"
Desse modo, tem-se: sen ((alfa)" − 900°) + cos ((alfa)" − 540°) = −sen (alfa)" + (−cos (alfa)") = −sen (alfa)" − cos (alfa)"
c) Pelos arcos kôn-gru-us, sabe-se quê:
4(pi)" = 2 ⋅ 2(pi)" ⇒ sen (4(pi)" − (alfa)") = sen (2(pi)" − (alfa)") = −sen (alfa)"
8(pi)" = 4 ⋅ 2(pi)" ⇒ cos (8(pi)" − (alfa)") = cos (2(pi)" − (alfa)") = cos (alfa)"
720° = 2 ⋅ 360° ⇒ sen (720° − (alfa)") = (360° − (alfa)") = −sen (alfa)"
Desse modo, tem-se: sen (4(pi)" − (alfa)") + cos (8(pi)" − (alfa)") − sen (720° − (alfa)") = −sen (alfa)" + cos (alfa)" − (−sen (alfa)") = cos (alfa)"
24. a) Sabe-se quê o valor do cosseno de um ângulo é positivo no 1º e no 4º quadrantes e quê o valor do seno de um ângulo é positivo no 1º e no 2º quadrantes. Logo, (alfa)" está no 1º quadrante.
b) Sabe-se quê o valor do cosseno de um ângulo é negativo no 2º e no 3º quadrantes e quê o valor do seno de um ângulo é positivo no 1º e no 2º quadrantes. Logo, (alfa)" está no 2º quadrante.
25. Para representar o seno de um ângulo na circunferência quando se conhece seu valor, primeiro localiza-se esse valor no eixo y e, em seguida, verificam-se os pontos na circunferência cuja projeção é o valor do seno. Para finalizar, encontram-se os ângulos responsáveis por esses pontos.
Página trezentos e setenta e oito
a) Dividir em 4 partes e considerar OP = ⋅ OD
b) Dividir em 10 partes e considerar OQ = ⋅ OB
c) Dividir em 5 partes e considerar OR = ⋅ OB.
26. Como (alfa)" = , segue quê:
A = sen − 3 sen 2(alfa)" +
A = sen () − 3 sen(2 ⋅ ) +
A = sen − 3 sen (pi)" + ⋅ sen = − 0 −
A =
27. Como sen (pi)" = 0, então:
2 sen (pi)" ⋅ sen ((pi)" − (alfa)") ⋅ sen ( + (alfa)") = 0.
28. Considerando a expressão sen 8(pi)" + sen − sen e como 8(pi)" e 2(pi)" são kôn-gru-us, pode-se concluir quê: sen 8(pi)" = sen 2(pi)" = 0.
+ 2 ⋅ 2(pi)" ⇒ sen = sen = −1
+ 2(pi)" ⇒ sen = sen =
Logo: sen 8(pi)" + sen − sen = 0 + (−1) − .
29. Calculando a razão trigonométrica de cada item, obtêm-se:
a) sen 120° = sen (180° − 60°) = sen 60° = (I)
b) sen 150° = sen (180° − 30°) = sen 30° = (II)
c) cos 120° = cos (180° − 60°) = −cos 60° = (IV)
d) cos 150° = cos (180° − 30°) = −cos 30° = (III)
e) sen () = sen () = sen(2(pi)" − ) = −sen = (IV)
f) sen = sen ((pi)" − ) = sen = (II)
g) cos (− ) = cos() = cos(2(pi)" − ) = cos = (I)
h) cos = cos((pi)" − ) = −cos = (III)
Portanto, conclui-se quê: a-I; b-II; c-IV; d-III; e-IV; f-II; g-I; h-III.
30. Sabendo quê cos x = e sen x = , segue quê m ≠ 0 e m ≥ −1.
Pela relação fundamental da Trigonometria, tem-se:
sen2 x + cos2 x = 1 ⇒ ()2 + ()2 = 1 ⇒m2 − m − 2 = 0
Resolvendo a última equação, obtém-se as soluções m’ = 2 e m” = −1.
Portanto, m = 2 ou m = −1.
31. a) Ao dividir 830° por 360°, obtém-se résto igual a 110° e, ao dividir 1.195° por 360°, obtém-se résto igual a 115°.
Pelo ciclo trigonométrico, sen 115° < sen 110°, porque ambos pertencem ao 2º quadrante. Portanto, sen 830° > sen 1.195°.
b) Ao dividir −535° por 360°, obtém-se résto igual a −175°.
Pelo ciclo trigonométrico, cos (−175°) = cos 185° < cos 190°, porque ambos pertencem ao 3º quadrante. Portanto, cos 190° > cos −535°.
32. Analisando a primeira determinação positiva dos arcos, tem-se:
+ 2(pi)"
31(pi)" = (pi)" + 15 ⋅ 2(pi)"
Desse modo: sen = sen = −1
cos 31(pi)" = cos (pi)" = −1
Ao substituir esses valores na expressão dada, obtém-se:
sen () ⋅ cos (31(pi)") = −1 ⋅ (−1) = 1
33. De acôr-do com as informações do enunciado, deve-se calcular a expressão a seguir:
cos (0 ⋅ ) + cos (1 ⋅ ) + cos (2 ⋅ ) + cos (3 ⋅ ) = 1 + 0 + (−1) + 0 = 0
34. Sabendo quê sen (alfa)" = e cos (alfa)" = a − 1, segue quê a ≥ 2.
Pela relação fundamental da Trigonometria, tem-se:
sen2 (alfa)" + cos2 (alfa)" = 1 ⇒ + (a − 1)2 = 1 ⇒ a2 − a − 2 = 0
Resolvendo a última equação, obtém-se as soluções a’ = 2 e a” = −1.
Como a ≥ 2, segue quê a = 2.
35. Pela relação fundamental da Trigonometria, tem-se:
(a + 2 + (a − )2 = 1 ⇒ 4a2 − 1 = 0
Ao resolver a última equação, obtêm-se as raízes:
a’ = e a” =
Logo: a =
36. a) sen 205° = sen (180° + 25°) = −sen 25° = −0,42
cos 205° = cos (180° + 25°) = −cos 25° = −0,91
b) sen (−25°) = sen (360° − 25°) = −sen 25° = −0,42
cos (−25°) = cos (360° − 25°) = cos 25° = 0,91
c) sen 335° = sen (360° − 25°) = −sen 25° = −0,42
cos 335° = cos (360° − 25°) = cos 25° = 0,91
37. a) Pesquisa dos estudantes. Uma sugestão seria trabalhar conceitos de etnomatemática como forma de explorar uma abordagem diferenciada com os estudantes. Também póde sêr interessante explorar o momento histórico e cultural vivido pelo Japão durante a criação dessas gravuras em madeira.
Página trezentos e setenta e nove
b) Considerando a ilustração do enunciado, pode-se afirmar quê o ângulo formado entre os centros de quaisquer dois círculos pequenos tangentes entre si e do círculo maior é 45°:
Agora, considere o triângulo isósceles cujos vértices são os centros das circunferências. A base méde 2t, e os lados congruentes médem r + t, no caso da circunferência concêntrica menor, ou R − t no caso da circunferência concêntrica maior.
Ao, destacar, no triângulo retângulo formado pela altura do triângulo isósceles, a mêtáde da base e um dos seus lados congruentes, podem-se obtêr as seguintes conclusões:
Logo, pode-se concluir quê:
sen (22,5°) = ⇒ 0,38(R − t) ≃ t ⇒ R ≃ 3,63t
sen (22,5°) = ⇒ 0,38(r + t) ≃ t ⇒ r ≃ 1,63t
c) Resposta pessoal. Espera-se quê os estudantes criem modelos geométricos similares ao apresentado na atividade, de modo a utilizar um conjunto de circunferências tangentes entre si e tangentes a uma circunferência maior. Espera-se também quê desenvolvam atividades quê exijam a determinação da medida de segmentos criados a partir dessa ilustração e quê possam sêr encontrados por meio de relações trigonométricas.
38. a) O arco de 150° pertence ao 2º quadrante, pois 90° < 150° < 180°.
Logo: tg 150° = tg (180° − 30°) = −tg 30° = .
b) O arco de −945° possui 1ª determinação negativa em −225°.
Logo, sua 1ª determinação positiva é 360° − 225° = 135°, cujo arco pertence ao 2º quadrante, pois 90° < 135° < 180°.
Logo: tg 135° = tg (180° − 45°) = −tg 45° = −1.
c) O arco é um arco do 4º quadrante, pois < < 2(pi)".
Logo: tg = tg (2(pi)"− ) = −tg =
d) O arco 7(pi)" possui 1ª determinação positiva em (pi)". Desse modo, tg 7(pi)" = tg (pi)" = 0.
39. Sabendo quê sen (alfa)" = e cos (alfa)" > 0, tomando o resultado positivo para cos (alfa)" dado pela relação fundamental da Trigonometria, tem-se:
sen2 (alfa)" + cos2 (alfa)" = 1 ⇒ + (cos (alfa)")2 = 1 ⇒ cos (alfa)" =
Desse modo, sabendo os valores de sen (alfa)" e cos (alfa)", pode-se calcular a tangente dêêsse arco: tg (alfa)" = .
40. A = sen 3(alfa)" + cos 4(alfa)" − tg 2(alfa)" = sen (3 ⋅ ) + cos (4 ⋅ ) − tg (2 ⋅ ) = −1 + 1 − 0 = 0
Logo, o valor da expressão é 0.
41. O arco de 510° possui 1ª determinação positiva igual a 150°. Desse modo:
cos 510° = cos 150° = cos (180° − 30°) = −cos 30° =
tg = tg ((pi)" − ) = −tg = −1
Assim: cos 510° + tg = − 1 =
42. Para verificar se tg 1 é maior ou menor do quê tg 7, pode-se converter 1 rad e 7 rad em grau e compará-los. Logo:
![]() ⇒ = ⇒ x ≃ 57°
⇒ = ⇒ x ≃ 57°
![]() ⇒ ⇒ x ≃ 401° (cuja primeira determinação é 41°)
⇒ ⇒ x ≃ 401° (cuja primeira determinação é 41°)
Como no primeiro quadrante a tangente é positiva e seus valores aumentam de acôr-do com o aumento do ângulo, então: tg 57° > tg 41°
Portanto: tg 1 > tg 7
• Resposta pessoal. Uma possibilidade seria observar quê uma volta completa na circunferência equivale a aproximadamente 6,28 rad. Assim, tg 7 é equivalente a aproximadamente tg (7 − 6,28) = tg 0,72 na primeira determinação positiva.
Logo, sêndo a tangente positiva no primeiro quadrante e sabendo quê seus valores aumentam de acôr-do com o aumento do ângulo nesse quadrante, segue quê: tg 1 > tg 0,72 = tg 7.
43. a) Considerando (alfa)" = calcula-se o valor da expressão: tg (alfa)" + tg 3(alfa)" + tg 5(alfa)" = tg + tg + tg = tg − tg + tg = 1
b) Considerando (alfa)" = −60°, calcula-se o valor da expressão: tg (alfa)" + tg 2(alfa)" + tg 4(alfa)" = tg (−60°) + tg (−120°) + tg (−240°) = −tg (60°) + tg (60°) − tg (60°) =
44. Para quê seja raiz da equação, deve-se substituir (alfa)" por e resolvê-la para determinar m:
(tg )2 − m (cos ) 2 + (sen 2 = 0 ⇒ − m ()2 + ()2 = 0 ⇒ m = 15
45. a) Pela relação fundamental da Trigonometria, obtém-se: sen2 (alfa)" + cos2 (alfa)" = 1 ⇒ (2 + cos2 (alfa)" = 1 ⇒ cos (alfa)" =
Como o arco é do segundo quadrante, conclui-se quê cos (alfa)" = .
b) tg (alfa)" = ⇒ tg (alfa)" = ⇒ tg (alfa)" =
Página trezentos e oitenta
46. Pela relação fundamental da Trigonometria, obtém-se:
sen2 (alfa)" + cos2 (alfa)" = 1 ⇒ (sen (alfa)")2 + = 1 ⇒ sen (alfa)" =
Como (alfa)" é um arco do terceiro quadrante, segue quê: sen (alfa)" =
Desse modo, sabendo o valor de sen (alfa)" e o de cos (alfa)", pode-se calcular a tangente dêêsse arco:
tg (alfa)" =
Por fim, calculando a expressão dada, obtém-se:
3sen (alfa)" + 4tg (alfa)" = 3 ⋅ () + 4 ⋅
Resposta: alternativa b.
47. Ao simplificar a expressão −tg2 (alfa)", conclui-se quê:
Aplicando a relação fundamental da Trigonometria, obtém-se:
48. tg x = ⇒ ⇒ sen x =
Pela relação fundamental da Trigonometria, obtém-se:
+ cos2 x = 1 ⇒ cos x =
Como o arco se encontra no terceiro quadrante, conclui-se quê cos x = . Logo:
sen x =
Por fim:
y = cos x − sen x =
49. Como 28° é um arco do primeiro quadrante, a tangente será positiva.
Como 230° é um arco do terceiro quadrante, a tangente será positiva.
Como 307° é um arco do quarto quadrante, a tangente será negativa.
Desse modo, pela regra de sinais, há uma multiplicação entre dois números positivos e um negativo, portanto o sinal do produto será negativo.
50. Verdadeiro.
Convertendo em grau, obtém-se 75°.
Portanto, será necessário verificar se tg 75° > sen 75°.
Sabe-se quê o valor mássimo para o seno de qualquer ângulo é 1; porém, tg 60° já é maior do quê 1, pois tg 60° = . Como tg 75° > tg 60° > 1, pode-se concluir quê tg 75° é maior do quê sen 75°, quê é menor do quê 1.
51. Como cos θ < 0 e tg θ < 0, conclui-se quê θ está localizado no segundo quadrante e, por isso, o valor de sen θ é positivo.
Pela relação fundamental da Trigonometria, obtém-se:
sen2 θ + = 1 ⇒ sen θ =
Portanto, a tg θ será:
tg θ =
Resolvendo a expressão proposta no enunciado, obtém-se:
x = ⇒ x = ⇒ x =
52. Aplicando a lei dos cossenos, tem-se:
(AB)2 = 802 + 1002 − 2 ⋅ 80 ⋅ 100 ⋅ cos 60° ⇒ (AB)2 = 6.400 + 10.000 − 16.000 ⋅ ⇒ AB = ≃ ±91, 65
Como o enunciado questiona a medida, 91,65 m é, aproximadamente, a medida de
53. Com base nas informações do enunciado, pode-se considerar a seguinte representação:
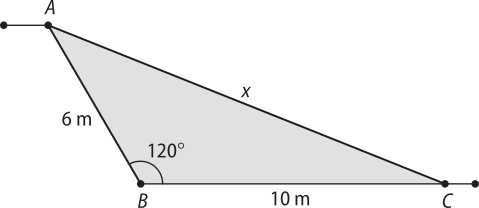
Aplicando a lei dos cossenos no triângulo ABC, tem-se:
x2 = 62 + 102 − 2 ⋅ 6 ⋅ 10 ⋅ cos 120° ⇒ x2 = 36 + 100 + 60 ⇒ x = 14
Logo, 14 m deve sêr o comprimento da rampa.
Resposta: alternativa e.
54. Aplicando a lei dos cossenos, tem-se:
(AB)² = 32² + 13² − 2 ⋅ 32 ⋅ 13 ⋅ cos 120° ⇒ (AB)² = 1.609 ⇒ AB ≃ 40,1
Portanto, 40 m é, aproximadamente, a distância entre os pontos A e B.
55. Utilizando o esquema a seguir, aplica-se a lei dos cossenos para determinar o ângulo (alfa)":
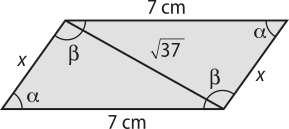
37 = x2 + 49 − 2 ⋅ x ⋅ 7 ⋅ cos (alfa)"
x2 − 14x ⋅ cos (alfa)" = −12
Como a medida x do lado do paralelogramo não é conhecida, é impossível determinar uma medida para o ângulo (alfa)". Isso também ocorrerá ao tentar determinar a medida do ângulo (beta)".
56. Com base nas informações contidas no enunciado, sabe-se AC = 2 cm e quê B é o ponto médio de , logo AB = 1 cm.
Além díssu, o (triângulo)"AEB é equilátero, então AE = EB = AB = 1 cm e o ângulo = 60°. Do (triângulo)"BCD é possível determinar quê = 60° e quê EB = BC = 1 cm.
Portanto, pode-se calcular a medida BD por meio da seguinte relação:
sen 30° = ⇒ BD = = 2
Sendo assim, aplicando a lei dos cossenos, determina-se quê a medida de , em centimetro, é:
(DE)2 = 12 + 22 − 2 ⋅ 1 ⋅ 2 ⋅ cos 60° ⇒ (DE)2 = 3 ⇒ DE =
Resposta: alternativa e.
57. Sabendo quê uma volta completa no relógio equivale a 360°, determina-se quê cada hora equivale a um arco de = 30°.
Logo, o ângulo entre os ponteiros é 60°, já quê o relógio marca duas horas.
Sendo assim, aplica-se a lei dos cossenos para determinar a distância x entre as extremidades do relógio:
x2 = 802 + 502 −2 ⋅ 80 ⋅ 50 ⋅ cos 60° ⇒ x2 = 4.900 ⇒ x = 70
A distância entre as extremidades dos ponteiros é 70 cm.
Página trezentos e oitenta e um
58. Aplicando a lei dos cossenos para um triângulo, pode-se calcular a medida BC, em centimetro:
(BC)2 = 52 + 62 − 2 ⋅ 5 ⋅ 6 ⋅ cos 60° ⇒ (BC)2 = 31 ⇒ BC ≃ 5,57
Logo, para cada triângulo é necessário 5 cm + 6 cm + 5,57 cm = 16,57 cm de fio. Como são 4 triângulos no total, Joana vai precisar de, aproximadamente, (4 ⋅ 16,57) cm = 66,28 cm de fio.
59. Com base nas informações do enunciado, pode-se considerar a seguinte imagem:
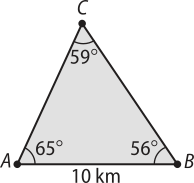
Na calculadora, pode-se obtêr as aproximações:
sen 56° = 0,82904
sen 65° = 0,90631
sen 59° = 0,85717
Aplicando a lei dos senos no triângulo ABC, tem-se:
⇒ AC ≃ 9,67
⇒ BC ≃ 10,57
Portanto, a distância aproximada da torre A até o foco do incêndio é 9,67 km e a distância aproximada da torre B até o foco do incêndio é 10,57 km.
60. Aplicando a lei dos senos, tem-se quê:
⇒ ⇒ sen (alfa)" =
61. a) Considerando o ângulo = (alfa)", conclui-se quê:
61° + 93° + (alfa)" = 180° ⇒ (alfa)" = 26°
Aplicando a lei dos senos no triângulo ABD, obtém-se:
⇒ ⇒ AD ≃ 49,43
A distância é de, aproximadamente, 49,43 m.
b) Considerando o triângulo ACD, obtém-se
sen 56° = ⇒ 0, 83 ⋅ 49, 43 ≃ h ⇒ h ≃ 41
O balão está a, aproximadamente, 41 m do solo.
62. Seja (alfa)" a medida do ângulo N ˆ B C:
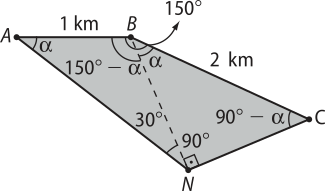
a) Pela lei dos senos, no triângulo ABN, tem-se:
= 2R ⇒ 2R = 2 ⋅ AB ⇒ R = 1
O raio da circunferência méde 1 km.
b) Ainda no triângulo ABN, pela lei dos senos, tem-se:
= 2 ⋅ R ⇒ sen (alfa)" = (I)
No triângulo retângulo BCN, por definição, tem-se:
cos (alfa)" = (II)
De (I) e (II), pode-se concluir quê sen (alfa)" = cos (alfa)". Como 0 < (alfa)" < 90°, segue quê (alfa)" = 45°. Desse modo:
NB = 2 ⋅ =
Portanto, a medida de é km.
63. Com base no triângulo ABC, considera-se quê = (gama)", logo:
(alfa)" + (beta)" + (gama)" = 180° ⇒ 75° + 60° + (gama)" = 180° ⇒ (gama)" = 45°
Aplicando a lei dos senos no triângulo ABC, pode-se concluir quê a medida de , em métro, é:
⇒ AC = 30 ⋅ = 15
Considerando o (triângulo)"ACD, pode-se concluir quê a medida de em métro, é:
tg 30° = ⇒ ⇒ cê dê = 15
Ao dividir cê dê por , obtém-se, em métro:
64. Considerando as informações do enunciado, pode-se obtêr o esquema a seguir.
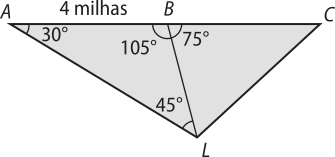
Aplicando a lei dos senos, obtém-se:
⇒ ⇒ BL =
A distância entre o farol e o ponto B é milhas.
65. a) Utilizando a informações contidas no enunciado, obtém-se:
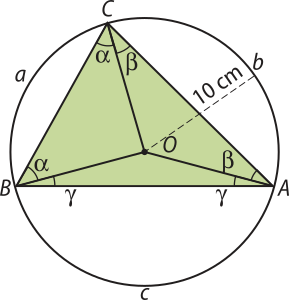
Como os arcos são proporcionais a 3, 4 e 5, então:
= = 30°
Logo:
med() ⇒ a = 3 ⋅ 30° = 90° ⇒ med() = 45°
med() ⇒ b = 4 ⋅ 30° = 120° ⇒ med() = 60°
med() ⇒ c = 5 ⋅ 30° = 150° ⇒ med() = 75°
b) Considerando o (triângulo)"COB, a medida de , em centimetro, é:
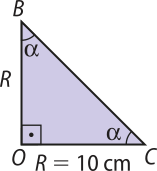
(BC)2 = R2 + R2 = 102 + 102 ⇒BC =
Página trezentos e oitenta e dois
Considerando o (triângulo)"COA, a medida de , em centimetro, é:
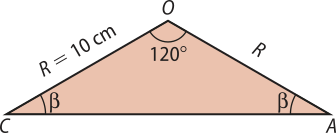
(CA)2 = R2 + R2 − 2 ⋅ R ⋅ R ⋅ cos 120° ⇒ CA2 = 2R2 − 2R2 ⇒ CA =
Considerando o (triângulo)"BOA, a medida de ¯ AB, em centimetro, é:
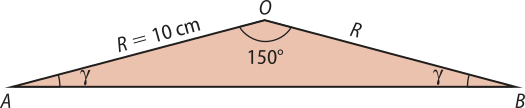
(AB)2 = R2 + R2 − 2 ⋅ R ⋅ R ⋅ cos 150°
(AB)2 = 2 R2 − 2 R2 ()
AB =
66. Utilizando o teorema da área de um triângulo qualquer, tem-se quê a área, em métro quadrado, é:
S = = 450
Resposta: alternativa e.
67. Considerando a representação a seguir e o teorema da área de um triângulo qualquer, pode-se resolver a atividade.
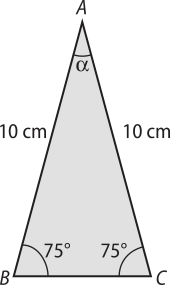
Nesse triângulo, o ângulo (alfa)" é dado por:
(alfa)" + 150° = 180° ⇒ (alfa)" = 30°
Logo, a área S do triângulo, em centimetro quadrado, é dada por:
S = = 25
68. Seja F a projeção do ponto D sobre o segmento . Da figura apresentada no enunciado, sabe-se quê a área total é dada por:
SABCDE = SABC + SAEDF + SFDC
Considerando o (triângulo)"ABC, determina-se a medida AC e, depois, FC:
(AC)2 = 402 + 382 − 2 ⋅ 40 ⋅ 38 ⋅ cos 60° ⇒ (AC)2 = 1.600 + 1.444 − 2 ⋅ 1.520 ⋅ ⇒ AC ≃ 39
FC ≃ 39 − 25 = 14
Assim, a área aproximada de ABCDE, em métro quadrado, é:
SABCDE ≃ + 30 ⋅ 25 +
SABCDE ≃ 760 ⋅ 0,86 + 750 + 210 = 1.613,60
preêço: 35,00 ⋅ 1.613,60 = 56.476
Portanto, o valor do terreno é, aproximadamente, R$ 56.476,00.
69. A figura a seguir foi construída com base nos dados do enunciado.
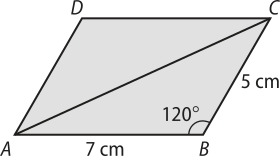
Nota-se quê a área do paralelogramo corresponde ao dôbro da área do triângulo ABC, cuja área, em centimetro quadrado, é dada por:
S(triângulo)"ABC =
Desse modo, a área do paralelogramo, em centimetro quadrado, é igual a:
S(triângulo)"ABC = 2 ⋅ cm2 =
70. Sabendo quê med() = 120°, tem-se quê med() = 30°, logo o (triângulo)"ABC é isósceles e BC = AC. Portanto, com base no teorema da área de um triângulo qualquer, obtém-se a medida AC quê, em centimetro, é:
SABC = ⇒ ⇒ AC = 10
Aplicando a lei dos cossenos, determina-se, em cm, a medida AB:
(AB)2 = 102 + 102 −2 ⋅ 10 ⋅ 10 ⋅ cos 120° ⇒ (AB) = ≃ 17
Portanto, o perímetro do triângulo é aproximadamente:
10 cm + 10 cm + 17 cm = 37 cm
71. A área total do hekzágono é igual a seis vezes a área de um triângulo equilátero de lado x. Logo, utilizando o teorema da área de um triângulo qualquer, tem-se quê a área do hekzágono, em centimetro quadrado, é:
Shex = 6 ⋅
72. Resposta pessoal. Exemplo de problema: Um terreno ABC será dividido em dois terrenos triangulares menóres ABD e ADC, conforme a figura a seguir.
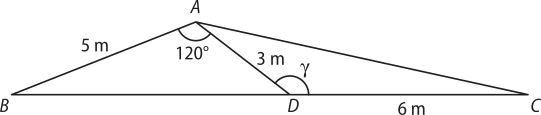
Qual é o perímetro do terreno ABD e qual é a área aproximada do terreno ADC? (Utilize sen (gama)" ≃ 0,62.)
Para calcular o perímetro de ABD, pode-se determinar a medida de .
Pela lei dos cossenos, tem-se a medida de em métro:
(BD)2 = 32 + 52 − 2 ⋅ 3 ⋅ 5 ⋅ cos 120° = 49 ⇒ BD = 7
Assim, o perímetro de ABD é igual a:
5 m + 3 m + 7 m = 15 m
Já a área do triângulo ADC, em métro quadrado, é aproximadamente:
SADC = = 5,58
Atividades complementares
1. Como a roleta foi dividida em 12 partes iguais, segue quê cada arco corresponde a um ângulo central de 360° ∶ 12 = 30°. Já um giro de 780° corresponde a:
780° = 60° + 2 ⋅ 360°
Desse modo, pode-se concluir quê a roleta deu duas voltas completas e mais 60° no sentido horário. Então, o número sorteado está a dois arcos no sentido anti-horário do 1, ou seja, o número sorteado é o 11.
Resposta: alternativa c.
Página trezentos e oitenta e três
2. 
A distância (d) percorrida pelo avião será: d = = 6.370(pi)".
d ≃ 3,14 ⋅ 6.370 ≃ 20.000
Portanto, 20.000 km é, aproximadamente, a distância percorrida.

x = ⇒ x = 25
Desse modo, chega-se em Singapura em 25 horas.
Resposta: alternativa c.
3. Convertendo 3 rad em grau, tem-se:

⇒ x ≃ 172°
Desse modo, sen 3 rad ≃ sen 172°, cuja extremidade encontra-se sobre o segundo quadrante. Nesse quadrante, os valores de seno varíam entre 0 e 1 e, à medida quê o ângulo aumenta, o valor do seno diminui. Logo:
sen 180° < sen 172° < sen 150° ⇒ 0 < sen 172° <
Portanto, sêndo y = sen 3, segue quê: 0 < y < .
Resposta: alternativa c.
4. Na circunferência trigonométrica, observa-se quê todos os possíveis valores de cosseno estão entre −1 e 1. Portanto:
−1 ≤ cos θ ≤ 1 ⇒ −1 ≤ ≤ 1 ⇒ −2 ≤ p ≤ 3
Resposta: alternativa c.
5. Na circunferência trigonométrica, observa-se quê todos os possíveis valores de seno estão entre −1 e 1. Portanto:
−1 ≤ sen x ≤ 1 ⇒ −1 ≤ m − 4 ≤ 1 ⇒ 3 ≤ m ≤ 5
Resposta: alternativa b.
6. Na circunferência trigonométrica, tem-se quê:
−1 ≤ cos (alfa)" ≤ 1
Assim: −1 ≤ cos (alfa)" ≤ 1 ⇒ −1 ≤ ≤ 1 ⇒ −1 ≤ x2 ≤ 4.
Logo, −1 ≤ x2 ou x2 ≤ 4. Para quê o arco x exista, êste deve sêr um número real e, portanto, desconsidera-se −1 ≤ x2. Então, para x2 ≤ 4, tem-se: x’ ≤ 2 ou x” ≥ −2.
Então: −2 ≤ x ≤ 2.
Resposta: alternativa b.
7. O ângulo central de um pentágono regular méde:
(alfa)" = = 72° ou rad Partindo do ponto P1, pode-se afirmar quê:
P2 =
P3 =
P4 =
Resposta: alternativa d.
8. Elevando ambos os membros da primeira relação ao quadrado, obtêm-se:
(sen (alfa)" + cos (alfa)")2 = ⇒ sen2 (alfa)" + cos2 (alfa)" + 2sen (alfa)" ⋅ cos (alfa)" = m
Porém, pela relação fundamental da Trigonometria, obtém-se:
1 + 2sen (alfa)" ⋅ cos (alfa)" = m
Como sen (alfa)" ⋅ cos (alfa)" = , então:1+2 ⋅ = m ⇒ 2m − n = 2.
Resposta: alternativa a.
9. Sabendo quê 0 ≤ (alfa)" < , pela redução do seno ao primeiro quadrante, tem-se:
sen (2(pi)" − (alfa)") = −sen (alfa)"
Já pela relação fundamental da Trigonometria:
sen2 (alfa)" + cos2 (alfa)" = 1 ⇒ (sen (alfa)")2 + = 1 ⇒ sen (alfa)" =
Como (alfa)" é um arco do primeiro quadrante, sen (alfa)" = e, portanto, −sen (alfa)" = .
Resposta: alternativa c.
10. Como sen (alfa)" = e (alfa)" está no segundo quadrante, conclui-se quê o cosseno e a tangente de (alfa)" são negativos.
Pela relação fundamental da Trigonometria, obtém-se:
cos2 (alfa)" = 1 − sen2 (alfa)" ⇒ cos (alfa)" =
Como a tg (alfa)" = , então:
tg (alfa)" =
Resposta: alternativa c.
11. Sendo x um arco do segundo quadrante, segue quê cos x < 0.
Assim, pela relação fundamental da Trigonometria:
sen2 x + cos2 x = 1 ⇒ + (cos x)2 = 1 ⇒ cos x = Desse modo, tem-se:
A = tg x =
Ao analisar os arcos da primeira determinação positiva em quê sen (alfa)" = , tem-se (alfa)"= ou (alfa)" = . Já os arcos em quê cos (alfa)" = , ocorrem quando (alfa)" = ou (alfa)" = . Logo, A = cos .
Resposta: alternativa b.
12. Sabe-se quê:
cos 200° = −cos 20°
sen 200° = −sen 20°
tg 200° =
Como cos 0° = sen 90° = 1, cos 90° = sen 0° = 0 e cos 45° = sen 45°, sabe-se quê, para arcos do primeiro quadrante, enquanto o ângulo for maior do quê 45°, o seno dêêsse ângulo é maior do quê o cosseno; enquanto for menor, o cosseno é maior do quê o seno.
Portanto: cos 20° > sen 20° e −cos 20° < −sen 20°. Logo, pode-se afirmar quê cos 200° < sen 200°.
Agora, como sen 200° e cos 200° são negativos, a tg 200° é positiva, sêndo maior do quê o cosseno e do quê o seno. Portanto: cos 200° < sen 200° < tg 200°.
Resposta: alternativa b.
Página trezentos e oitenta e quatro
13. Sendo 270° < x < y < 360°, pode-se observar quê x e y pertencem ao 4º quadrante e quê x < y. Então:
Como no quarto quadrante o valor do cosseno é positivo, se x < y, conclui-se quê cos y > cos x e, por sêr o seno negativo, sen y > sen x.
Como sen x < 0 e cos y > 0, então sen x ⋅ cos y < 0.
Como x e y pertencem ao quarto quadrante, o sinal da tangente nesses quadrantes é negativo, logo tg x < tg y.
Sabe-se quê cos y > sen x; dessa forma, cos y − sen x > 0.
Resposta: alternativa d.
14. Considerando as informações contidas no enunciado, pode-se afirmar quê um lado méde 8 m e o perímetro do terreno é 20 m.
Então os outros dois lados podem sêr definidos como x e 12 − x.
Aplicando a lei dos cossenos:
x2 = (12 − x)2 + 82 − 2 ⋅ 8 ⋅ (12 − x) ⋅ cos 60°
x2 = 144 − 24x + x2 + 64 − 96 + 8x ⇒ x = 7
Portanto, os lados médem 7 m e 5 m
Resposta: alternativa b.
15. Do triângulo do enunciado, tem-se quê med() = 45°. Logo, ao aplicar a lei dos senos, obtém-se a medida de , em centimetro:
⇒ AB = ≃ 16,97
Conforme a atividade menciona, convertendo para a escala real, tem-se:
AB = 16,97 cm ⋅ ≃ 1,7 km Resposta: alternativa e.
16. Aplicando a lei dos cossenos, tem-se a medida de BC, em centimetro: (BC)2 = 102 + 102 − 2 ⋅ 10 ⋅ 10 ⋅ cos 120° ⇒ BC = ≃ 17.
Como o raio méde aproximadamente 17 cm, então o material será do tipo IV.
Resposta: alternativa d.
17. Sejam b e (éli)" as medidas dos lados opostos do triângulo, respectivamente, aos ângulos (beta)" e de 30°, pela lei dos senos proposta na atividade, tem-se:
b = 2R ⋅ sen (beta)" = 2 ⋅ 4 cm ⋅ = 7,5 cm
(éli)" = 2R ⋅ sen 30° = 2 ⋅ 4 cm ⋅ = 4 cm
Logo, o perímetro do triângulo é igual a:
4 cm + 7,5 cm + 7,9 cm = 19,4 cm
Resposta: alternativa b.
18. Aplicando o teorema de Pitágoras aos (triângulo)"ABC e (triângulo)"ABD, determinam-se as medidas de e , respectivamente:
(AC)2 = 22 + 12 ⇒ AC =
(AD)2 = 22 + 62 ⇒ AC =
Sendo assim, por meio da lei dos cossenos, determina-se o ângulo θ:
52 = − 2 ⋅ ⋅ cos θ ⇒ cos θ =
Logo, θ = 45°.
Resposta: alternativa c.
19. Considerando as informações contidas no enunciado, tem-se quê med() = 120°, logo med() = 30°. Sendo assim, o (triângulo)"BCD é isósceles e cê dê = BD. Portanto, tem-se:
cos 60° = ⇒ ⇒ BD = 6
SABD = q = =
SBCD = p =
Logo, pela relação ôbitída, tem-se p = 2q.
Resposta: alternativa b.
20. Segundo as informações do enunciado, é possível determinar quê DC = 3 e quê CE = 5. Além díssu, med() = 90° + 60° = 150°. Desse modo, pela lei dos cossenos, tem-se:
(DE)2 = 32 + 52 2 ⋅ 3 ⋅ 5 ⋅ cos 150° = 34 − 30 ⋅ ⇒ DE =
Resposta: alternativa e.
Capítulo 6 • Funções trigonométricas
Atividades
1. Como a função seno é periódica, em cada item dessa atividade, considera-se a função y dada e determinam-se alguns pontos (x, y) para o esboço do gráfico dessa função. Esses pontos são indicados nos quadros. Para o esboço indicado em cada item, considerou-se apenas um período, mas os gráficos podem sêr representados em todo o eixo x.
a) Seja y = 3 ⋅ sen x, então:
x |
sen x |
3 ⋅ sen x |
y |
|---|---|---|---|
0 |
0 |
3 ⋅ 0 |
0 |
1 |
3 ⋅ 1 |
3 |
|
(pi)" |
0 |
3 ⋅ 0 |
0 |
−1 |
3 ⋅ (−1) |
−3 |
|
2(pi)" |
0 |
3 ⋅ 0 |
0 |
D = ℝ; Im = [−3, 3]; p = 2(pi)"
Página trezentos e oitenta e cinco
b) y = 2 − sen x
x |
sen x |
2 − sen x |
y |
|---|---|---|---|
0 |
0 |
2 − 0 |
2 |
1 |
2 − 1 |
1 |
|
(pi)" |
0 |
2 − 0 |
2 |
−1 |
2 − (−1) |
3 |
|
2(pi)" |
0 |
2 − 0 |
2 |
D = ℝ; Im = [1, 3]; p = 2(pi)"
c) Como y = sen (x − ), pode-se fazer a substituição: t = x − ⇒ x = t +
t |
x |
sen t |
y |
|---|---|---|---|
0 |
sen 0 |
0 |
|
(pi)" |
sen |
1 |
|
(pi)" |
sen (pi)" |
0 |
|
2(pi)" |
sen |
−1 |
|
2(pi)" |
sen 2(pi)" |
0 |
D = ℝ; Im = [−1, 1]; p = 2(pi)"
d) Como y = 2 sen , pode-se fazer a substituição:
t = ⇒ x = 4 ⋅ t
t |
x |
sen t |
2 ⋅ sen t |
y |
|---|---|---|---|---|
0 |
0 |
0 |
2 ⋅ 0 |
0 |
2(pi)" |
1 |
2 ⋅ 1 |
2 |
|
(pi)" |
4(pi)" |
0 |
2 ⋅ 0 |
0 |
6(pi)" |
−1 |
2 ⋅ (−1) |
−2 |
|
2(pi)" |
8(pi)" |
0 |
2 ⋅ 0 |
0 |
D = ℝ; Im = [−2, 2]; p = 8(pi)"
2. Seja p = o período da função y = sen (cx + d).
a) Para y = sen 8x: p = .
b) Para y = 5 ⋅ sen 10x: p = .
3. Sabendo quê a função seno tem valor mínimo −1 e mássimo 1, tem-se:
7 ⋅ (−1) ≤ 7 ⋅ sen (3x) ≤ 7 ⋅ 1 ⇒ −7 ≤ 7 ⋅ sen (3x) ≤ 7
Portanto, Im = [−7, 7].
4. Como f(x) = sen (2x + ), o período de f é dado por p = sêndo c = 2. Assim: p = = (pi)".
Resposta: alternativa b.
5. a) Considerando 4 ⋅ sen (alfa)" e sabendo quê −1 ≤ sen (alfa)" ≤ 1:
4 ⋅ (−1) ≤ 4 ⋅ sen (alfa)" ≤ 4 ⋅ 1 ⇒ −4 ≤ 4 sen (alfa)" ≤ 4
Logo, o valor mássimo é 4 e o valor mínimo é −4.
b) Considerando 5 − 2 ⋅ sen x, tem-se:
−1 ≤ sen x ≤ 1 ⇒ 5 + (− 2) ⋅ (−1) ≥ 5 − 2 ⋅ sen x ≥ 5 + (−2) ⋅ 1 ⇒ 7 ≥ 5 −2 sen x ≥ 3
Logo, o valor mássimo é 7 e o valor mínimo é 3.
c) A expressão terá valor mássimo quando o denominador for mínimo.
Como o valor mínimo para sen y é −1, para sen y = −1 o valor de é mássimo, ou seja, .
Analogamente, a expressão terá valor mínimo quando o denominador for mássimo. Isso ocorre quando sen y = 1.
Logo, é mínimo para:
Assim, o valor mássimo de é e o valor mínimo é
6. Considerando quê sen x = 2m − 1 e como −1 ≤ sen x ≤ 1, então:
−1 ≤ 2m − 1 ≤ 1 ⇒ 0 ≤ m ≤ 1
S = {m ∈ ℝ | 0 ≤ m ≤ 1}
7. Para verificar qual é a afirmativa correta, deve-se analisar o mínimo, o mássimo, o período e os zeros de cada função.
• Para f(x) = 2 ⋅ sen (x), tem-se:
−1 ≤ sen x ≤ 1 ⇒ −2 ≤ 2 ⋅ sen (x) ≤ 2
p = = 2(pi)"
Os zeros da função 2 ⋅ sen (x) ocorrem quando sen (x) = 0, ou seja, quando x = k ⋅ (pi)", para k ∈ ℤ.
• Para g(x) = sen (2x), tem-se:
−1 ≤ sen (2x) ≤ 1
p = = (pi)"
Os zeros da função sen (2x) ocorrem quando sen (2x) = 0, ou seja, quando x = k ⋅ , para k ∈ ℤ.
Dessa forma, observa-se quê o período da função f é o dôbro do período da g.
Resposta: alternativa a.
Página trezentos e oitenta e seis
8. Assumindo quê −1 ≤ sen x ≤ 1 é possível afirmar quê:
−1 ≤ ≤ 1
Em relação a ≤ 1, tem-se quê:
≤ 1 ⇒ −1≤0 ⇒ ≤ 0
Considerando f(k) = 4k + 1 e g(k) = k − 3, pode-se realizar o estudo do sinal de .
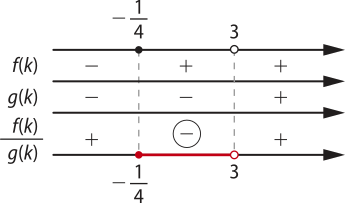
Portanto, segue quê: {k ∈ ℝ | ≤ k < 3} (I)
Em relação a ≥ −1, tem-se quê: ≥ −1 ⇒ + 1 ≥ 0 ⇒ ≥ 0.
Considerando f(minutos)"(k) = 6k − 5 e g(minutos)"(k) = k − 3, pode-se realizar o estudo do sinal de .
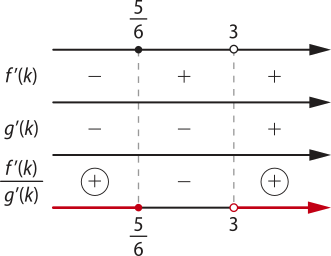
Portanto, segue quê: {k ∈ ℝ | k ≤ ou k > 3} (II)
Fazendo (I) ∩ (II), temos:
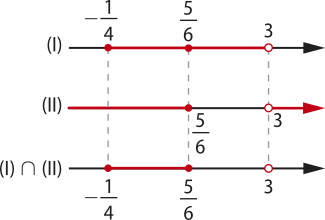
Logo, S = {k ∈ ℝ | ≤ k ≤ }.
9. O valor de seno de um ângulo qualquer deve estar compreendido entre −1 e 1. Logo:
−1 ≤ sen θ ≤ 1 ⇒−1 ≤ ≤ 1⇒ −1 ≤ x ≤ 2
Resposta: alternativa d.
10. Considere f(x) = 900 − 800 ⋅ sen ().
Como −1 ≤ sen () ≤ 1, conclui-se quê:
Para sen () = 1: f(x) = 900 − 800 ⋅ 1 = 100.
Para sen () = −1: f(x) = 900 − 800 ⋅ (−1) = 1.700.
Logo, o número mássimo de clientes é 1.700 e o mínimo é 100, sêndo sua diferença igual a 1.600.
Resposta: alternativa e.
11. Seja V(t) = y + z ⋅ sen (t), com y, z e t ∈ ℝ, z > 0.
Considerando Vmínimo = 2 e Vmássimo = 4 o menor e o maior valor de V(t), respectivamente, e sabendo quê o valor mínimo de sen (t) é −1, e o valor mássimo de sen (t) é 1, tem-se:
Vmínimo = y + z ⋅ (−1) ⇒ 2 = y − z (I)
Vmássimo = y + z ⋅ 1 ⇒ 4 = y + z (II)
Resolvendo o sistema formado pelas equações (I) e (II), obtém-se y = 3 e z = 1. Dessa forma:
V(t) = 3 + 1 ⋅ sen (t) ⇒ V(t) = 3 + sen (t)
Resposta: alternativa e.
12. Resposta pessoal. Espera-se quê os estudantes criem situações-problema a partir de fenômenos periódicos quê possam sêr descritos ou aproximados pela função seno dada. Dessa maneira, eles podem elaborar enunciados quê tratem do mássimo ou do mínimo da função, de seu período, seus zeros e sua imagem.
13. Como a função cosseno é periódica, em cada item dessa atividade, considera-se a função y dada e determinam-se alguns pontos (x, y) para o esboço do gráfico dessa função. Esses pontos são indicados nos quadros. Para o esboço indicado em cada item, considerou-se apenas um período, mas os gráficos podem sêr representados em todo o eixo x.
a) y = −cos x
x |
cos x |
y = −cos x |
|---|---|---|
0 |
1 |
−1 |
0 |
0 |
|
(pi)" |
−1 |
1 |
0 |
0 |
|
2(pi)" |
1 |
−1 |

b) Como y = 3 cos pode-se fazer a substituição:
t = ⇒ x = 2t
t |
x |
cos t |
y = 3 cos t |
|---|---|---|---|
0 |
0 |
1 |
3 |
(pi)" |
0 |
0 |
|
(pi)" |
2(pi)" |
−1 |
−3 |
3(pi)" |
0 |
0 |
|
2(pi)" |
4(pi)" |
1 |
3 |
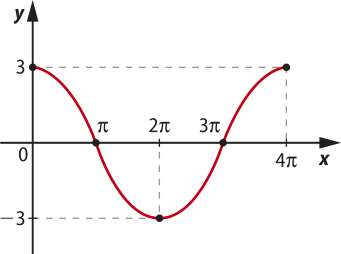
Página trezentos e oitenta e sete
c) y = 5 + cos x
x |
cos x |
y = 5 + cos x |
|---|---|---|
0 |
1 |
6 |
0 |
5 |
|
(pi)" |
−1 |
4 |
0 |
5 |
|
2(pi)" |
1 |
6 |
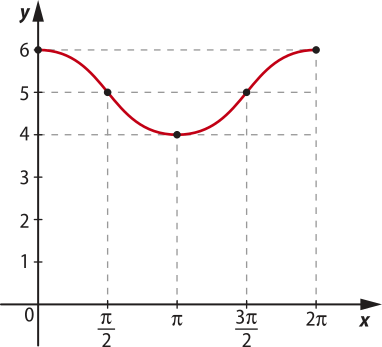
d) Como y = cos (x − ), pode-se fazer a substituição: t = x − ⇒ x = t +
t |
x |
y = cos |
|---|---|---|
0 |
1 |
|
0 |
||
(pi)" |
−1 |
|
0 |
||
2(pi)" |
1 |
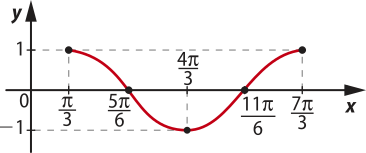
14. Seja p = o período da função y = b ⋅ cos (cx + d).
a) Para y = cos 8x: p = .
b) Para y = 5 cos 10x: p = .
c) Para y = cos :p = .
d) Para y = 6 cos : p = = 8(pi)".
15. Seja p o período da função. Então: p = ⇒ ⇒ m = 4.
16. A expressão terá valor mássimo quando o valor do denominador for mínimo, ou seja, quando cos x assume valor mínimo. Assim, para cos x = −1:
= 5
17. Considere sen x0 = cos x0. Pela relação fundamental da Trigonometria, tem-se:
sen2 x0 + cos2 x0 = 1 ⇒ cos2 x0 + cos2 x0 = 1 ⇒ cos x0 =
Dessa forma, a função f(x) = 110(sen x + cos x) assumirá valor mássimo para sen x0 = cos x0 = e mínimo para .
Assim, o valor mássimo da função é dada por:
f(x0) = 110(sen x0 = cos x0) = 110 ⋅ 2 ⋅ = .
Resposta: alternativa a.
18. Se o ponto (0, 2) pertence à função f(x) = a + cos x, então:
2 = f(0) = a + cos 0 ⇒ 2 = a + 1 ⇒ a = 1
Dessa forma, f(x) = 1 + cos x e, portanto, tem-se:
f(2(pi)") = 1 + cos 2(pi)" = 1 + 1 = 2
Resposta: alternativa c.
19. Se os pontos (, 1) e (0, −1) pertencem à função f(x) = a − b cos x, então:
1 = f() = a − b ⋅ cos ⇒ 1= a − b ⋅ 0 ⇒ a = 1
−1 = f(0) = a − b ⋅ cos 0 ⇒ −1 = 1 − b ⋅ 1 ⇒ b = 2
Dessa forma, f(x) = 1 − 2 cos x e, portanto, tem-se:
f((pi)") = 1 − 2 ⋅ cos (pi)" = 1 − 2 ⋅ (−1) = 3
Resposta: alternativa a.
20. Dada f(x) = 3 ⋅ cos x + 2 e sabendo quê −1 ≤ cos x ≤ 1, conclui-se quê:
3 ⋅ (−1) + 2 ≤ 3 ⋅ cos x + 2 ≤ 3 ⋅ 1 + 2 ⇒ −1 ≤ 3 ⋅ cos x + 2 ≤ 5
Portanto, o conjunto imagem da função f é [−1, 5].
21. Seja f(x) = b ⋅ cos (cx) a forma geral da função descrita pelo gráfico. Por meio dele, é possível observar quê a função contém o ponto (0, 2). Dessa forma:
2 = f(0) = b ⋅ cos (c ⋅ 0) ⇒ 2 = b ⋅ 1 ⇒ b = 2
Além díssu, pelo gráfico, o período p da função é . Logo:
p = ⇒ ⇒ c = ± 4
Portanto, f(x) = 2cos (−4x) ou f(x) = 2cos (4x).
Resposta: alternativa d.
22. a) f(x) = 2cos x
g(x) = 2sen x
f((pi)") ⋅ g((pi)") = 2cos (pi)" ⋅ 2sen (pi)" = 2−1 ⋅ 20 =
b) f() =
g() =
Como , conclui-se quê f() > g().
23. a) Considere quê a altura da maré é dada por:
A(t) = cos (t − a) + b.
Além díssu, sabe-se quê, às 4:00 (t = 4), a altura registrada foi mássima (3 m). Logo: A(4) = cos (4 − a) + b = 3.
O valor A(4) é mássimo quando cos (4 − a) é 1, então:
4 − a = 0 ⇒ a = 4
Logo: A(t) = cos (t − 4) + b.
Disso vêm quê b = 2, pois:
A(4) = cos (4 − 4) + b = 3 ⇒ 1 + b = 3 ⇒ b = 2
Portanto, A(t) = cos (t − 4) + 2, ou seja, a = 4 e b = 2.
b) Resposta pessoal. Exemplo de atividade: De acôr-do com as informações contidas no qüadro, determine:
a) Qual é o período da maré?
b) Durante o dia, quais são os melhores horários para frequentar a praia com segurança?
Respostas:
a) Olhando os momentos de pico, a maré atinge a maior altura às 4:00, às 10:17 e às 16:34. Logo, o período é de 6 horas e 14 minutos.
b) Os melhores horários para frequentar a praia em segurança são nos momentos em quê a maré está mais baixa, ou seja, por volta das 7:08 da manhã e por volta das 13:25.
Página trezentos e oitenta e oito
24. a) Sabe-se quê sen e quê sen (ângulos notáveis).
sen x = ⇒ x = ou x =
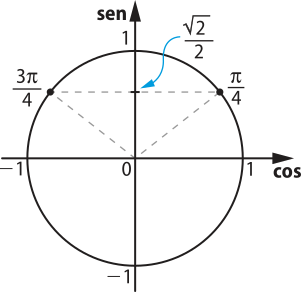
S = {}
b) Sabendo quê cos = , pela redução ao primeiro quadrante da função cosseno, tem-se:
cos ((pi)" − ) = cos () = −cos =
cos ((pi)" + ) = cos () = −cos =
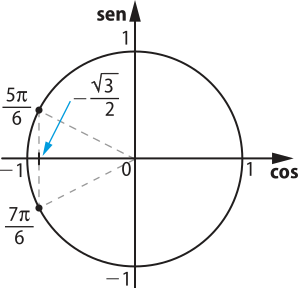
Assim, pode-se afirmar quê:
cos x = ⇒ x = ou x = .
Portanto: S = {}.
c) Como sen x = −1, então x = , pois, dos valores notáveis do seno, sabe-se quê sen = −1.
S =
d) Como cos x = −1, então x = (pi)", pois sabe-se quê cos (pi)" = −1.
S = {(pi)"}
25. a) Isolando o seno na equação, obtém-se:
2 sen x + 1 = 0 ⇒ sen x =
Sabendo quê sen , pela redução ao primeiro quadrante da função seno, tem-se:
sen ((pi)" + ) = sen () = −sen =
sen (2(pi)" − ) = sen () = −sen =
S ={x ∈ ℝ | x = + 2 k(pi)" ou x = + 2 k(pi)", k ∈ ℤ}
b) Isolando o seno na equação, obtém-se:
2 sen 2x = 1 ⇒ sen 2x = .
Sabendo quê sen pela redução ao primeiro quadrante da função seno, tem-se:
sen ((pi)" − ) = sen () = sen =
Logo:
2x = + 2k(pi)" ⇒ x = + k(pi)"; ou 2x = + 2k(pi)" ⇒ x = + k(pi)"
S ={x ∈ ℝ | x = + k(pi)" ou x = + k(pi)", k ∈ ℤ}
26. Resolvendo a equação trigonométrica, obtém-se:
sen (2x − ) = ⇒ sen(2x − ) = sen
Logo∶
2x − +2k(pi)"⇒2x = +2k(pi)"⇒x = + k(pi)"
2x − = (pi)" − +2k(pi)"⇒2x = +2k(pi)"⇒x = + k(pi)"
S = {x ∈ ℝ | x = +k(pi)" ou x = +k(pi)", k ∈ ℤ}
27. Resolvendo a equação trigonométrica, obtêm-se:
sen 4x = 1 ⇒ sen 4x = sen
Logo:
4x = + 2k(pi)" ⇒ x = ⋅ k(pi)"
S = {x ∈ ℝ | x = (pi)", k ∈ ℤ}
Resposta: alternativa d.
28. Considerando as informações do enunciado, conclui-se quê:
I(t) = 40 sen (120(pi)"t) ⇒ 20 = 40 sen (120(pi)"t) ⇒ = sen (120(pi)"t) ⇒ sen = sen (120(pi)"t) ⇒ 120(pi)"t = ⇒ t = ≃ 0,0014
Logo, o tempo mínimo para o gerador produzir uma corrente de 20 amperes é de aproximadamente 0,0014 segundos.
29. a) Ao considerar a equação 2sen2 x − 6sen x − 8 = 0, deve-se substituir sen x = y, então:
2sen2 x − 6sen x − 8 = 0 ⇒ 2y2 − 6y − 8 = 0
Ao resolver a última equação do 2º grau, obtêm-se as raízes y(minutos)" = 4 e y(segundos)" = −1.
Como 4 > 1, não se deve considerar a solução positiva, pois sen x ≤ 1.
Sendo assim, como sen x = y, tem-se:
sen x = −1 ⇒ sen = −1 ⇒ x = + 2k(pi)"
S = {x ∈ ℝ | x = + 2k(pi)", k ∈ ℤ}
b) Ao considerar a equação cos2 x + cos x = 0, deve-se substituir cos x = y, então:
cos2 x + cos x = 0 ⇒ y2 + y = 0
Ao resolver a última equação do 2º grau, obtêm-se as raízes y(minutos)" = 0 e y(segundos)" = −1.
Como cos x = y, tem-se:
• Para cos x = 0:
cos = 0 ou cos = 0 ⇒ x = + 2k(pi)" ou x = + 2k(pi)" ⇒ x = + k(pi)"
Página trezentos e oitenta e nove
• Para cos x = −1:
cos (pi)" = −1 ⇒ x = (pi)" + 2k(pi)"
S = {x ∈ ℝ | x = + k(pi)" ou x = (pi)" + 2k(pi)", k ∈ ℤ}
30. Considerando sen2 x = y, tem-se sen4 x = y2. Ao substituir na equação, obtém-se:
2 sen4 x − 3 sen2 x + 1 = 0 ⇒ 2y2 − 3y + 1 = 0
Ao resolver a equação do 2º grau, obtêm-se as raízes y(minutos)" = 1 e y(segundos)" = .
Como sen2 x = y, então: sen2 x = 1 e sen2 x =
• Considerando sen2 x = 1, tem-se sen x = ±1. Então:
Para sen x = 1: sen x = sen ⇒ x = + 2k(pi)"
Para sen x = −1: sen x = sen ⇒ x = + 2k(pi)"
Portanto, x = + k(pi)".
• Considerando sen2 x = , tem-se sen x = . Então:
Para sen x = : sen x = sen = sen ⇒ x = + 2k(pi)" ou x = + 2k(pi)"
Para sen x = : sen x = sen = sen ⇒ x = + 2k(pi)" ou x = + 2k(pi)"
Portanto, x = + k(pi)" ou x = + k(pi)".
S = {x ∈ ℝ | x = + k(pi)" ou x = + k(pi)" ou x = + k(pi)", k ∈ ℤ}
31. Ao substituir sen x = a na equação dada, obtém-se:
4−sen x = ⇒ 4−a = ⇒ a =
Logo, sen x = . Sabendo quê sen , pela redução ao primeiro quadrante da função seno, tem-se:
sen ((pi)" − ) = sen () = sen
Portanto, x = + 2k(pi)" ou x = + 2k(pi)".
S = {x ∈ ℝ | x = + 2k(pi)" ou x = + 2k(pi)", k ∈ ℤ}
32. Para resolver a equação deve-se considerar quê cos ((pi)" − x) póde assumir um valor positivo e um negativo, pois está em módulo. Portanto:
cos ((pi)" − x) =
Sabendo quê cos pela redução ao primeiro quadrante da função cosseno, tem-se:
cos ((pi)" − ) = cos () = −cos
cos ((pi)" + ) = cos () = − cos
cos (2(pi)" − ) = cos () = cos
Portanto:
(pi)" − x = + k(minutos)"(pi)" ⇒ x = + k(pi)" ou (pi)" − x = + k(minutos)"(pi)" ⇒ x = + k(pi)".
S = {x ∈ ℝ | x = + k(pi)" ou x = + k(pi)", k ∈ ℤ}
33. Seja y = sen x. Dessa forma, pela relação fundamental da Trigonometria, tem-se:
2 cos2 x + 3 sen x − 3 = 0 ⇒ 2 ⋅ (1 − sen2 x) + 3 sen x − 3 = 0 ⇒ −2y2 + 3y −1 = 0
Resolvendo esta última equação, obtém-se y(minutos)" = 1 e y(segundos)" =
Portanto, sen x = 1 ou sen x = .
Para x ∈ [0, 2(pi)"], tem-se quê sen x = 1 se x = e sen x = se x = ou x = .
Dessa forma, nesse intervalo, a equação tem três soluções.
Resposta: alternativa d.
34. Sendo P e Q os pontos de intersecção dos gráficos das funções y1 = sen (x + 1) e y2 = e percebendo quê ambos pertencem a um mesmo período da função y1, pode-se determinar seus valores tomando sen (x + 1) = para os valores de x em uma mesma volta na circunferência trigonométrica.
Sabendo quê sen , pela redução ao primeiro quadrante da função seno, tem-se:
sen ((pi)" + ) = sen () = −sen
sen (2(pi)" − ) = sen () = −sen
Logo, tem-se quê:
x + 1 = ⇒ x = ou x + 1 = ⇒ x =
Portanto, conclui-se quê
PQ =
Resposta: alternativa b.
35. O mês de produção mássima ocorre quando o preêço é mínimo.
O preêço será mínimo quando cos () for mínimo. Assim:
cos () = −1 ⇒ = (pi)" ⇒ x = 7
Portanto, a produção mássima ocorre em julho.
Resposta: alternativa d.
36. Segundo o enunciado, o pistão precisa alcançar a altura de 6 cm por três vezes em menos de 4 segundos. Então, deve-se calcular os possíveis instantes de tempo em quê a altura alcançará 6 cm, ou seja, h(t) = 6:
h(t) = 4 + 4 sen () ⇒ 6 = 4 + 4 sen () ⇒ sen
Portanto, isso ocorrerá quando sen .
Observe agora a circunferência trigonométrica:
Na primeira volta, para quê h(t) = 6, deve-se considerar os arcos: e .
O terceiro arco ocorre na segunda volta, ou seja, para: + 2(pi)" = .
Assim, como (beta)" ≠ 0, o instante de tempo t em quê ocorrerá essa terceira ocorrência será:
⇒ t =
Página trezentos e noventa
Como esta ocorrência deve ocorrer antes de t = 4 e, tomando (pi)" = 3, tem-se:
< 4 ⇒ (beta)" > ⇒ (beta)" > 4
Portanto, o menor valor inteiro para (beta)" é 5.
Resposta: alternativa d.
Atividades complementares
1. Substituindo x = na função f(x) = 4 ⋅ sen (2x), tem-se:
f() = 4 ⋅ sen (2 ⋅ ) = 4 ⋅
Resposta: alternativa c.
2. Sejam f(x) = sen (1 + ) (pi)" e g(x) = sen (1 − )(pi)". Daí, tem-se:
K = f(9) ⋅ g(9) = [sen (1 + )(pi)"] ⋅ [ sen (1 − )(pi)"] = sen ⋅ sen −
Como a função seno é periódica e simétrica em relação à origem, então:
sen = sen + 2 ⋅ 2(pi)" = sen = −1;
sen − = −sen + 2(pi)" = −sen = 1.
Portanto, segue quê K = −1 ⋅ 1 = −1.
Resposta: alternativa b.
3. Sejam P(5) e P(8) os pesos em maio e agosto, respectivamente, dados em kg:
P(5) = 65 − 5 cos((pi)") = 65 − 5 cos = 65 + 5 cos () = 65 + = 67,5
P(8) = 65 − 5 cos( (pi)") = 65 − 5 cos = 65 − 5 cos () = 65 − = 65 − 4, 25 = 60,75
Fazendo P(8) − P(5):
60,75 − 67,5 = −6,75
Portanto, o peso da pessoa diminuiu 6,75 kg.
Resposta: alternativa 03.
4. A altura mássima de H(t) = 5 + 3 sen (2t), em métro, ocorrerá quando o valor do seno for mássimo, isto é, quando sen (2t) = 1: Hmássima = 5 + 3 ⋅ sen (2t) = 5 + 3 ⋅ 1 = 8
Resposta: alternativa e.
5. Seja f(x) cos ( + (pi)") + 3 = f(x − )(x − (pi)" ⋅ sen (x)).
Substituindo x = nesta expressão, obtém-se:
f() cos ( + (pi)") + 3 = f(( − (pi)" ⋅ sen ()) ⇒ f() cos ( + (pi)") + 3 = f(0)( − (pi)") ⇒ −f() cos () + 3 = f(0)() ⇒ ⋅ f() + 3 = f(0)()
Calculando f(0) na expressão dada, obtém-se:
f(0) cos ( + (pi)") + 3 = f(0 − )(0−(pi)"⋅sen(0)) ⇒ f(0) cos ((pi)") + 3 = f(−)(0) ⇒ −f(0) + 3 = 0 ⇒ f(0) = 3
Portanto, segue quê:
⋅ f() + 3 = 3 ⋅ () ⇒ f() =
Resposta: alternativa e.
6. Os gráficos se interceptam quando 1 + sen x = 1 − cos x, com 0 ≤ x ≤ 2(pi)", ou seja, quando sen x = −cos x.
Na circunferência trigonométrica a seguir, são apresentados os arcos em quê sen x e cos x possuem os mesmos valores absolutos:
Os valores de seno e cosseno têm sinais opostos no segundo e no quarto quadrantes, ou seja, quando x = e x = .
Resposta: alternativa e.
7. A interseção dos gráficos de f(x) = sen (x) e g(x) = cos (x) ocorrerá quando sen (x) = cos (x). Considerando essa igualdade, pela relação fundamental da Trigonometria, tem-se:
sen2 x + cos2 x = 1 ⇒ cos2 x + cos2 x = 1 ⇒ cos x =
Logo, os pontos P(xk, yk) da interseção de f e g possuem valores para yk iguais a
Resposta: alternativa a.
8. Como p(t) = 100 − 20sen (t), para t ≥ 0, conclui-se quê 80 ≤ p(t) ≤ 120, uma vez quê −1 ≤ sen t ≤ 1. Disso, obtém-se quê a diferença entre o valor mássimo e o mínimo da função p(t) é igual a 120 − 80 = 40. Como essa diferença corresponde ao diâmetro da circunferência, então o diâmetro méde 40.
Resposta: alternativa b.
9. A função f(x) = 3 − 5sen (2x + 4) terá valor mássimo e mínimo, respectivamente, quando sen (2x + 4) assumir valor mínimo de −1 e mássimo de 1. Assim:
• quando sen (2x + 4) = −1, f(x) = 3 − 5(−1) = 8 (valor máximo)
• quando sen (2x + 4) = 1, f(x) = 3 − 5 ⋅ 1 = −2 (valor mínimo)
O período p é dado por: p = = (pi)".
Resposta: alternativa b.
10. Considerando f(x) = 3sen2 x + 7cos2 x e pela relação fundamental da Trigonometria, tem-se:
f(x) = 3sen2 x + 7cos2 x = 3 ⋅ (1 − cos2 x) + 7 cos2 x = 3 + 4 cos2 x
Como −1 ≤ cos x ≤ 1, segue quê 0 ≤ cos2 x ≤ 1. Logo:
Para cos2 x = 0: f(x) = 3 + 4 ⋅ 0 = 3
Para cos2 x = 1: f(x) = 3 + 4 ⋅ 1 = 7
Logo, M = 7 e m = 3 e, dessa forma, M ⋅ m = 21.
Resposta: alternativa c.
11. Dada f(x) = 2 − 3 cos x e sabendo quê −1 ≤ cos x ≤ 1, segue quê:
Para cos x = −1: f(x) = 2 − 3 ⋅ (−1) = 5
Para cos x = 1: f(x) = 2 − 3 ⋅ 1 = −1
Dessa forma, Im(f) = [−1, 5].
Resposta: alternativa e.
12. Seja f(x) = 5 − 3 cos (). Seu período é igual a:
p = =2(pi)"⋅(pi)"=2(pi)"2
Como −1 ≤ cos x ≤ 1, segue quê:
Para cos x = −1: f(x) = 5 − 3 ⋅ (−1) = 8
Para cos x = 1: f(x) = 5 − 3 ⋅ 1 = 2
Dessa forma, Im(f) = [2, 8].
Resposta: alternativa c.
Página trezentos e noventa e um
13. Pelo gráfico de f(x) = a + b ⋅ sen x, o ponto (0, 1) pertence a essa função. Logo:
f(0) = a + b ⋅ sen 0 ⇒ a + b ⋅ 0 = 1 ⇒ a = 1
Sabe-se quê, para x ∈ [0, ], a função g(x) = sen x é crescente.
Mas, no gráfico da f(x) = 1 + b ⋅ sen x, para valores de x a partir de zero, a função inicialmente decresce. Logo, b < 0.
Ainda pelo gráfico, sabe-se quê 3 é ponto mássimo da função f.
Como b < 0, esse valor de mássimo ocorre quando o seno é mínimo. Desse modo, para sen x = −1:
3 = 1 + b ⋅ (sen x) ⇒ 2 = b ⋅ (−1) ⇒ b = −2
Resposta: alternativa d.
14. Ao considerar as informações contidas no enunciado, sabe-se quê a função P(t) = A + Bcos (kt), em quê −1 ≤ cos (x) ≤ 1, possui imagem 78 ≤ P(t) ≤ 120. Portanto, como B é positivo, tem-se:
⇒ A = 99 e B = 21
Como são 90 batimentos por minuto e o intervalo entre cada batimento representa o período p, tem-se:
p =
Além díssu, sabe-se quê p = . Portanto, como k é positivo, segue quê:
p = ⇒ k = 3(pi)"
Logo, P(t) = 99 + 21 ⋅ cos (3(pi)"t).
Resposta: alternativa a.
15. O período de g(x) = (alfa)" ⋅ sen (beta)"x é 4(pi)", uma vez quê ele equivale ao dôbro do período da função f(x) = sen x, cujo período é 2(pi)". Então:
4(pi)" = ⇒ (beta)" =
Logo, 0 < (beta)" < 1.
Como a amplitude de g(x) é menor do quê a de f(x), pode-se afirmar quê 0 < (alfa)" < 1.
Resposta: alternativa a.
16. Analisando o gráfico da função, percebe-se quê ela possui um deslocamento vertical e uma mudança de amplitude em relação à função g(t) = sen t. Dessa forma, considere quê a função é dada por f(t) = A ⋅ sen t + B.
Para determinar A e B, deve-se analisar alguns pontos pertencentes à função:
Para t = 0: f(0) = 88 ⇒ 88 = A ⋅ sen 0 + B ⇒ B = 88 (I)
Para t = : f() = 168 ⇒ 168 = A ⋅ sen + B ⇒ A + B = 168 (II)
Substituindo (I) em (II), conclui-se quê A = 80 e, portanto,
f(t) = 80 ⋅ sen t + 88.
Resposta: alternativa a.
17. Como −1 ≤ cos (2(pi)"t) ≤ 1, o valor mássimo e o valor mínimo de P(t) ocorrem, respectivamente, quando cos (2(pi)"t) = 1 e quando cos (2(pi)"t) = −1.
I. Verdadeira. P(t) = 96 + 18 ⋅ 1 = 96 + 18 = 114
II. Verdadeira. P(t) = 96 + 18 ⋅ (−1) = 96 − 18 = 78
III. Verdadeira. O período da função é = 1
IV. Falsa. P() = 96 − 18 ⋅ cos () = 96 + 18 ⋅ () = 96 − 9 = 87
V. Falsa. Sendo P(0) = 114, o gráfico apresentado não é o de P(t).
Resposta: I: V; II: V; III: V; IV: F; V: F.
18. Seja D(t) = M + N sen ((alfa)"t) a distância do assento 1 até o solo a cada t segundos.
Pelo enunciado, o período da função é 30 segundos. Logo, como (alfa)" > 0:
p = ⇒30 = ⇒ (alfa)" = .
Sabe-se também quê, para t = 0, D(t) é equivalente ao raio da roda-gigante mais a altura do ponto mais baixo da roda em relação ao solo. Logo:
D(0) = M + N sen () ⇒ 10,5 = M + N ⋅ sen (0) ⇒ M = 10,5
Além díssu, o ponto mais alto na roda-gigante corresponde a uma altura em relação ao solo de 20,5 m, quê ocorre quando t = 30 ∶ 4 = 7,5. Logo:
D(7,5) = M + N sen () ⇒ 20,5 = 10,5 + N ⋅ sen() ⇒ N = 10
Portanto: M − N = 10,5 − 10 = 0,5 = .
Sabe-se quê cos Logo, para(alfa)" = , tem-se:
= cos = cos () = cos (5(alfa)")
Resposta: alternativa a.
19. Como n é par, tem-se:
sen (x + (pi)") + sen (x + 2(pi)") = 0
sen (x + 3(pi)") + sen (x + 4(pi)") = 0.
…
sen (x + (n − 1) (pi)") + sen (x + n(pi)") = 0
Portanto:
sen (x)+ sen (x + (pi)")+ sen (x + 2(pi)")+ sen (x + 3(pi)")+ … + sen (x + n(pi)") = sen (x)
Resposta: alternativa a.
20. Resolvendo a equação trigonométrica para x ∈ [0, 2(pi)"], obtém-se:
sen 2x = 1 ⇒ sen 2x = sen
Logo:
2x = ⇒ x =
Resposta: alternativa c.
21. Como a embarcação precisa de uma profundidade mínima de 2 m, ou seja, h(t) = 2, deve-se encontrar os momentos do dia em quê isso ocorre. Logo:
h(t) = 3 − 2sen () ⇒ 2 = 3 − 2sen () ⇒ sen () =
Sabe-se quê o valor de seno é para e . Então:
⇒ t = 2 ou ⇒ t = 10
Como a medição começou a ocorrer às 6 h da manhã, então, nesse momento, t = 0.
As soluções encontradas são t = 2, quê corresponde a 8 h, e t = 10, quê corresponde a 16 h.
Como o navio estava encalhado às 11 h, ele precisará esperar até as 16 h, ou seja, esperar mais 5 horas.
Resposta: alternativa b.
22. A função r(t) = terá valor mássimo quando o denominador for mínimo, ou seja, quando cos (0,06t) = −1, e terá valor mínimo quando o denominador for mássimo, isto é, quando cos (0,06t) = 1.
rmássimo = = 6.900
rmínimo = = 5.100
Dessa forma, S = 6.900 km + 5.100 km = 12.000 km.
Resposta: alternativa b.
Página trezentos e noventa e dois
Capítulo 7 • Áreas
Atividades
1. a) Ao decompor a figura em dois retângulos, obtém-se:
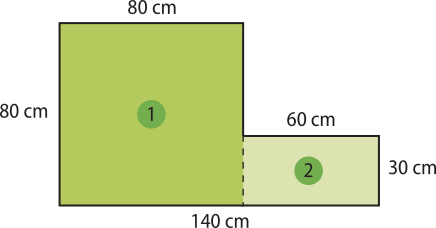
S = S1 + S2 ⇒ S = 802 + 60 ⋅ 30 ⇒ S = 8.200
Portanto: S = 8.200 cm2.
b) A área S, em cm2, é:
S = = 18
c) O semiperímetro p, em cm, do triângulo é:
p = ⇒ p = 12
Assim, a área S, em cm2, é:
S = ⇒ S =
d) Seja S1 a área do triângulo retângulo em m2:
S1 = ⇒ S1 = 600
A base maior do trapézio retângulo é a hipotenusa de um triângulo retângulo cujos catetos médem 30 m e 40 m.
Assim, pelo teorema de Pitágoras, essa base tem medida de 50 m.
Seja S2 a área do trapézio retângulo em m2:
S2 = ⇒ S2 = 1.350
Então, a área da figura, em m2, é:
S = S1 + S2 ⇒ S = 1.950
2. De acôr-do com as informações apresentadas, as dimensões do mural são 21 m de altura por 8 m de largura e a superfícíe da parede lateral do edifício em quê ele foi pintado é retangular. Assim, a área S, em m2, dêêsse mural é:
S = 8 ⋅ 21 = 168
3. a) Há 100 quadradinhos de 1 cm2 contidos inteiramente na região delimitada pela figura. Logo: Sfalta = 100 cm2.
b) Há 148 quadradinhos de 1 cm2 contidos inteiramente ou parcialmente na região delimitada pela figura. Logo: Sexcésso = 148 cm2
c) S = = 124 cm2
d) ≃ 0, 0368 = 3, 68%
4. Considerando as informações contidas no enunciado, pode-se afirmar quê, se a área do quadrado de lado (éli)" é dada por S = (éli)"2, então, depois de aumentar seu lado em 4 cm, a área final será Sf = ((éli)" + 4)2. Como, ao aumentar o lado, a área aumenta 56 cm2, então:
Sf = S + 56 ⇒ ((éli)" + 4)2 = (éli)"2 + 56 ⇒ (éli)"2 + 8(éli)" + 16 = (éli)"2 + 56 ⇒ (éli)" = 5
Assim, como d = , tem-se a medida d, em cm: d =
5. Ao aumentar o lado de um quadrado em 20%, obtém-se:
S = ((éli)" + 0,2(éli)")2 = (1,2(éli)")2 = 1,44(éli)"2
Como a área do quadrado é definida por SQ = (éli)"2, então, S = 1,44 ⋅ SQ.
Portanto, a área do quadrado aumenta 44%.
6. a) As áreas da parede, Sp, e de cada azulejo, Sa, em cm2, são, respectivamente:
Sp = 500 ⋅ 350 = 175.000
Sa = 202 = 400
Assim, o número de azulejos necessários é dado por:
= 437,5
São necessários 437,5 azulejos.
b) Para não havêer a necessidade de kórti, o valor procurado deve sêr o maior possível entre os divisores de 350 e de 500.
Assim, o valor x inteiro e positivo deve sêr x = mdc(350, 500).
Como 350 = 2 ⋅ 52 ⋅ 7 e 500 = 22 ⋅ 53, tem-se:
x = 2 ⋅ 52 = 50
A maior dimensão de cada peça de azulejo deve sêr 50 cm.
7. Inicialmente, a largura e o comprimento do terreno podiam sêr divididos, respectivamente, na seguinte quantidade de partes:
= 500; = 1.200
Assim, o agricultor podia plantar, no mássimo, 600.000 mudas, pois:
500 ⋅ 1.200 = 600.000
Depois da ampliação, a largura e o comprimento do terreno podem sêr divididos, respectivamente, na seguinte quantidade de partes:
= 2.000; = 500
Assim, o agricultor poderá plantar, no mássimo, 1.000.000 mudas, pois:
2.000 ⋅ 500 = 1.000.000
Isso indica quê a quantidade mássima de mudas quê poderão sêr plantadas a mais é 400.000.
Resposta: alternativa b.
8. A área S dos retângulos azuis é dada por:
S = x ⋅ (21 − x) + (27 − x) ⋅ x ⇒ S = −2x2 + 48x
Como a área deve sêr mássima, deve-se encontrar xV, dado em cm.
Assim:
xV = ⇒ xV = ⇒ xV = 12
Logo, a soma das áreas será a maior possível quando x = 12 cm.
9. A área da região clara póde sêr calculada por meio do quádruplo da área do triângulo APB, visto quê os triângulos APB, APD, CQD e CQB são congruentes e possuem as mesmas áreas. Logo, a área de cada um dêêsses triângulos, em m2, é:
SAPB =
Portanto, a área clara, em m2, é: Sclara = 4 ⋅ = 0,25
A área sombreada, em m2, é dada por: Ssombreada = 1 − 0,25 = 0,75
Calcula-se o preêço P do vitral por meio do produto da área de cada região pelo preêço do m2 correspondente:
P = 0,25 ⋅ 50 + 0,75 ⋅ 30 = 35
Portanto, o custo será de R$ 35,00.
Resposta: alternativa b.
10. Pode-se representar a situação com a seguinte figura:
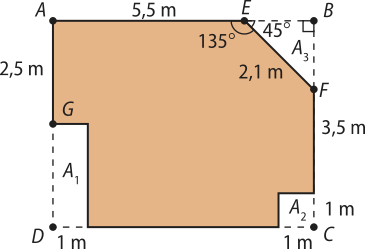
Página trezentos e noventa e três
Considerando a representação, pode-se concluir quê a área do apartamento é equivalente à área do retângulo ABCD subtraídas as áreas A1, A2 e A3.
O triângulo EBF é retângulo e isósceles. Dessa forma, BF = EB, e sua medida x, em métro, pelo teorema de Pitágoras é:
(2, 1)2 = x2 + x2 ⇒ x = ≃ 1, 5
Considerando como aproximada a área do apartamento, seja BF = 1,5 m. Desse modo, BC = AD = 6 m e, portanto, GD = 3,5 m.
Assim, as seguintes áreas, em m2, são iguais a:
A1 = 1 ⋅ 3,5 = 3,5
A2 = 1 ⋅ 1 = 1
A3 = = 1,125
AABCD = DC ⋅ BC = 7 ⋅ 6 = 42
Assim, a área do apartamento, em m2, será aproximadamente igual a A = AABCD − (A1 + A2 + A3) = 36,375.
Considerando a observação do mestre de obras, a quantidade de piso a sêr comprada, em m2, será igual a 1,1 ⋅ 36,375 = 40,0125 ≃ 40.
Resposta: alternativa c.
11. Como ABCD é um retângulo, cada ângulo destacado em C méde 90° ∶ 3 = 30°.
Sendo h a medida da altura do retângulo, podemos calcular a medida AC usando a relação trigonométrica cosseno no triângulo retângulo ABC:
cos 60° = ⇒ ⇒ AC = 2h
Além díssu, podemos calcular a medida CE usando a relação trigonométrica cosseno no triângulo retângulo BCE:
cos 30° = ⇒ ⇒ CE =
Utilizando a fórmula trigonométrica para o cálculo da área de triângulos, obtemos a área S do triângulo sombreado AEC:
S =
A área S(minutos)" do retângulo ABCD é o dôbro da área do triângulo ABC.
Desse modo, temos:
S(minutos)" = 2 ⋅ = 2h ⋅ h ⋅
Assim, a razão entre as áreas S e S’ é:
Logo, a área do triângulo sombreado AEC é igual a da área total do retângulo.
Resposta: alternativa b.
12. Atividade de construção de horta. Ainda quê não seja viável a implementação das propostas dos estudantes, a atividade possibilita quê eles reflitam sobre o meio em quê vivem e percêbam como os conceitos de área e de perímetro são úteis em propostas práticas.
13. O raio r, em dm, é dado por:
S = (pi)"r2 ⇒ 100(pi)" = (pi)" ⋅ (r)2 ⇒ r = ±10
Como r é o raio da circunferência, desconsidera-se r = −10 e, além díssu, como o diâmetro é o dôbro do raio, d = 20 dm.
14. De acôr-do com as informações contidas no enunciado, pode-se afirmar quê:
Squadrado = (éli)"2 e Scírculo =
Srestante = (éli)"2 − (éli)"2 ≃ 0,80(éli)"2
Logo, a área restante equivale a aproximadamente 80% da área do quadrado.
Resposta: alternativa d.
15. Como 1.300 m = 13 hm, a área em hm2 irrigada por esse pivô é:
S = (pi)"r2 ⇒ S ≃ 3,14(13)2 = 530,66.
Como 1 hm2 = 1 ha, então o pivô consegue irrigar uma área aproximada de 530,660 ha.
16. A área da região azul é igual à área da região branca, ou seja, é a mêtáde da circunferência:
S = = 2(pi)"r2
Como r = 10 cm, tem-se quê S, em cm2, é:
S ≃ 2 ⋅ 3,14 ⋅ 102 ⇒ S ≃ 628
Logo, a área azul méde aproximadamente 628 cm².
17. O raio de uma pitssa de 8 pedaços méde 16 cm. Precisa-se determinar o diâmetro da nova pitssa de 12 pedaços, de modo quê a área de cada pedaço seja igual à área de um pedaço da pitssa antiga, ou seja:
⇒ r = ≃ ± 20
Como r é o raio do círculo, desconsidera-se r = −20. Logo, o diâmetro da pitssa nova é aproximadamente 40 cm.
Resposta: alternativa b.
18. A área S da coroa circular, em m2, é:
S = (pi)"( ⇒ S = (pi)"(52 − 32) ⇒ S = 16(pi)"
19. Sabe-se quê 30° = . Assim, a área S, em cm2, destacada em vêrde na figura é:
S = ⇒ S = ⋅ (pi)" (502 − 402) ⇒ S = 75(pi)"
20. De acôr-do com as informações contidas no enunciado, pode-se considerar a figura a seguir:
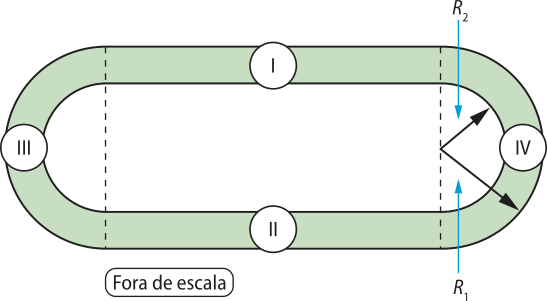
(I) e (II) são retângulos cujas dimensões são 100 m e 3 m.
(III) e (IV) representam uma coroa circular de raios:
R1 = 23 m e R2 = 20 m
A área S, em m2, da calçada é a soma da área das regiões I, II, III e IV.
S = 2 ⋅ 100 ⋅ 3 + (pi)"(232 − 202)
S = 600 + 129(pi)" ⇒ S ≃ 1.005,06
O custo, em reais, é dado por 50 ⋅ S. Logo, o custo total da obra será de aproximadamente R$ 50.253,00.
21. Do enunciado, tem-se R + r = 1, pois os círculos com centro em vértices consecutivos do quadrado são tangentes e, portanto, R + r corresponde à medida do lado dêêsse quadrado. É possível aferir quê R + R corresponde à diagonal do quadrado, portanto:
2R = ⇒ R =
Portanto:
r =1 −
Assim, a área sombreada S é dada por:
S = 1 − = 1 − ⇒ S = 1 + (pi)"( − 1)
Resposta: alternativa e.
Página trezentos e noventa e quatro
22. De acôr-do com as informações contidas no enunciado, pode-se afirmar quê a medida do raio e a do apótema, em cm, são dadas por:
a) (éli)" = ⇒ 6 = ⇒ r =
b) m = ⇒ m =
23. A medida do lado do hekzágono regular é igual ao raio da circunferência circunscrita, isto é, (éli)" = r. Por isso, o hekzágono regular póde sêr decomposto em seis triângulos equiláteros congruentes cujos lados médem 2 cm.
A área de cada um dêêsses triângulos, em cm2, é dada por:
S = ⇒ S =
Logo, a área SH do hekzágono, em cm2, será:
SH = ⇒ SH ≃ 6 ⋅ 1,73 = 10,38 ⇒ S ≃ 10,38.
24. De acôr-do com as informações contidas no enunciado, pode-se afirmar quê as áreas das figuras, em cm2, são:
a) S = 5 ⋅ ⇒ S = 200
b) S = 6 ⋅ ⇒ S =
25. A área Sq de cada quadrado e a área Sh do hekzágono, em cm2, são iguais a:
Sq = (éli)"2 = 102 = 100
Sh = 6 ⋅ ≃ 259, 5
Logo, a área total S da figura, em cm2, é de aproximadamente: S = 6Sq + Sh = 859,5.
26. Considerando m, (éli)" e p as respectivas medidas do apótema, do lado e do semiperímetro do triângulo, dadas, em cm, e S sua área, dada, em cm2, tem-se:
m = ⇒ 3 = ⇒ r = 6
(éli)" = ⇒ (éli)" =
p = ⋅ (éli)" ⇒ p = ⇒ p =
S = p ⋅ m = ⋅ 3 =
27. a) Sejam L a medida do lado do quadrado circunscrito à circunferência e (éli)" medida do lado do quadrado inscrito a ela.
Então, L = 2r e (éli)" = .
b) Si = 2r2 e Sc = (2r)2 = 4r2
28. Sabe-se quê m = cm.
a) Como (éli)" = r, a medida de (éli)" em cm será:
m = ⇒ ⇒ (éli)" = 12
b) A área Sh do hekzágono de lado (éli)" corresponde a seis vezes a área S(triângulo)" de um triângulo equilátero de mesmo lado. Assim, a medida dessa área, em cm2, é de:
Sh = 6 ⋅ S(triângulo)" = 6 ⋅
29. Para calcular a área sombreada, deve-se subtrair a área do quadrado de lado a u.c. da área da circunferência circunscrita a esse quadrado. A diagonal dêêsse quadrado será u.c. e, portanto, o raio da circunferência méde u.c. Assim, a área Sc da circunferência, em u.a., será:
Sc = (pi)" ⋅
A área do quadrado é a2 u.a.; assim, a área sombreada, Ss, em u.a., será:
Ss = − a2 = a2 ( −1)
30. Como o perímetro do polígono regular considerado é dado pelo produto entre a medida do lado e 10, o polígono possui 10 lados. Portanto, é um decágono regular.
31. Resposta pessoal. Exemplo de problema: Qual é a área de um hekzágono regular cujo perímetro méde 50 cm?
Como o perímetro é 50 cm, o semiperímetro é 25 cm e a medida do lado é cm. Portanto, a área S, em cm2, é:
S = 25 ⋅ ⇒ S = (104 + )
32. a) A medida m do apótema, em cm, é dada por:
m = ⇒ m = ⇒ m =
b) Sejam Shex. a área do hekzágono ABCDEF e Ssetor a área de cada setor circular. Então, a área vêrde S, em cm2, é dada por:
S = Shex. − 2 ⋅ Ssetor
Shex. = 6 ⋅ ⇒ Shex. =
Ssetor = ⇒ Ssetor =
S = − 2 ⋅ ⇒ S =
33. A área Sh do hekzágono regular é igual a seis vezes a área S(triângulo)" do triângulo equilátero de mesmo lado. Logo a área Sh, em cm2, é igual a:
Sh = 6 ⋅ S(triângulo)" = 6 ⋅
34. a) Como AO equivale à medida do raio da circunferência em quê o triângulo equilátero ABC está inscrito, então a medida (éli)" do lado, em cm, é:
(éli)" = = 12
b) A área limitada pela circunferência de centro O, em cm2, é:
Sc = 48(pi)"
O triângulo ABC tem altura equivalente a cm. Portanto, sua área é cm2. Assim, a área cinza, em cm2, será:
S = 48(pi)" − ≃ 88
35. De acôr-do com as informações contidas no enunciado, pode-se afirmar quê:
a) 
b) Como o octógono regular possui 8 lados congruentes, o perímetro P é dado por: P(m) = 8m.
c) 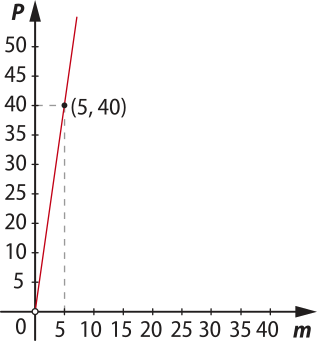
Página trezentos e noventa e cinco
36. a) A Figura 1 é o polígono regular de 3 lados (triângulo equilátero), cujo perímetro é 3 vezes a medida de seu lado. Logo,
P1(a) = 3a. Conforme estudado, a área de um triângulo equilátero de lado a é ; logo, S1(a) = . Em ambas as funções, devemos considerar para o domínio os valores de a reais positivos (pois a indica a medida do lado).
b) 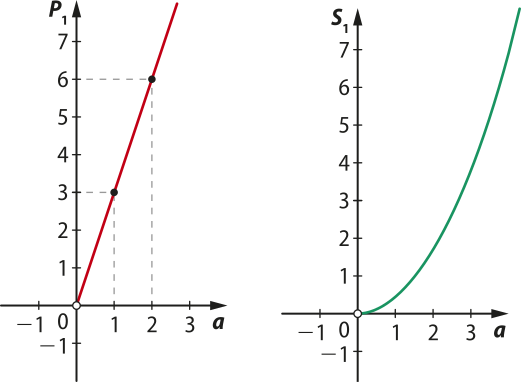
c) A Figura 2 é o polígono regular de 6 lados (hexágono regular), cujo perímetro é 6 vezes a medida de seu lado. Logo, P2(b) = 6b. Conforme estudado, a área de um hekzágono regular de lado b é ;logo, S2(b) = . Em ambas as funções, devemos considerar para o domínio os valores de b reais positivos (pois b é medida de lado).
d) 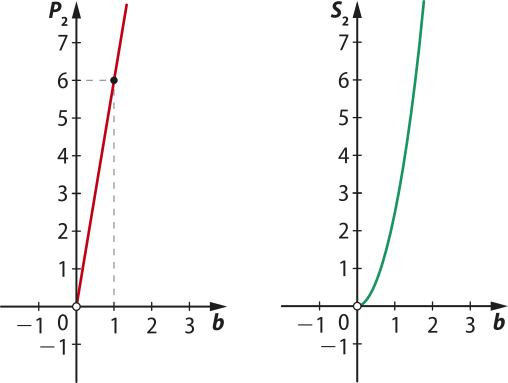
37. Calcula-se a área do material utilizada em cada caso. Considerando as áreas em m2 e a medida do raio em m, tem-se:
• tampa grande
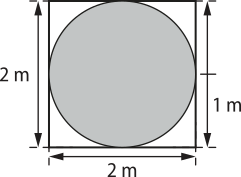
raio do círculo: 1 m
área utilizada, em m2: (pi)" ⋅ r2 = (pi)"
sóbra, em m2: 22 − (pi)" = (4 − (pi)")
• tampa média
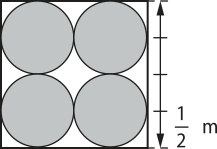
raio do círculo: m
área utilizada, em m2: 4 ⋅ (pi)" ⋅ r2 = 4 ⋅ (pi)" ⋅ = (pi)"
sóbra, em m2: 22 − (pi)" = (4 − (pi)")
• tampa pequena

raio do círculo: m
área utilizada, em m2: 16 ⋅ (pi)" ⋅ r2 = 16 ⋅ (pi)" = (pi)"
sóbra, em m2: 22 − (pi)" = (4 − (pi)")
Portanto, as três entidades recebem a mesma quantidade de material.
Resposta: alternativa e.
38. Sim, pois cada ângulo interno do hekzágono regular méde 120° e, do triângulo equilátero, méde 60°. Dessa maneira, 2 ⋅ 120° + 2 ⋅ 60° = 240° + 120° = 360°, quê é a soma necessária para obtêr o ladrilhamento.
39. a) Ao unir dois dodecágonos regulares e congruentes a fim de obtêr um ladrilhamento, obtém-se um ângulo de 300°, pois cada ângulo interno do dodecágono regular méde 150°. Portanto, a região não preenchida entre esses dois dodecágonos forma um ângulo de 60°, quê não comporta outro dodecágono.
b) Para obtêr o ladrilhamento, pode-se inserir um triângulo equilátero com lado congruente ao do dodecágono regular, pois o triângulo equilátero tem ângulos internos de 60°. Logo: 150° + 150° + 60° = 360°.
40. A única opção cujas medidas dos ângulos internos são divisores de 360° é o hekzágono regular, cujo ângulo interno méde 120°.
Resposta: alternativa e.
41. Tomando um vértice qualquer do ladrilhamento, há quatro polígonos quê o contêm: um triângulo equilátero, dois quadrados e um hekzágono regular. Começando pelo triângulo equilátero e seguindo no sentido anti-horário, temos a seguinte ordem: triângulo equilátero, quadrado, hekzágono regular e quadrado, quê se traduz na notação (3.4.6.4).
Resposta: alternativa e.
42. Para obtêr ladrilhamento, os ângulos internos dos polígonos com vértice em comum devem somar 360°.
Pode-se utilizar a expressão n ⋅ 135° + m ⋅ x = 360°, em quê n é o número de octógonos utilizados, com n = 1 ou n = 2.
Se n = 1, então o outro tipo de polígono a sêr utilizado deve ter ângulos internos quê possam somar exatamente 225° (não é possível).
Se n = 2, o outro tipo de polígono utilizado deve ter ângulos internos quê possam somar 90° (o quadrado).
Portanto, é possível ladrilhar com octógonos e quadrados.
Resposta: alternativa b.
43. Observando a figura 2, tem-se:
2 ⋅ 120° + 108° + x = 360° ⇒ x = 12°
Resposta: alternativa b.
Página trezentos e noventa e seis
Atividades complementares
1. Como a área do quadrado e do triângulo devem sêr iguais, tem-se:
x2 = ⇒ 3 x2 − 10x = 0 ⇒ x(3x − 10) = 0
Resolvendo as equações, obtém-se x(minutos)" = 0 ou x(segundos)" = .
Como x é a medida de um segmento, x = 0 não é uma solução.
Portanto: x = .
Resposta: alternativa c.
2. No triângulo ABN, como AM = MB e a altura relativa a esses lados em relação ao vértice N é a mesma, então:
SAMN = SMBN = t
No triângulo ABC, como AN = NC e a altura relativa a esses lados em relação ao vértice B é a mesma, então: SABN = SNBC.
Desse modo, a área do triângulo ABC é igual a:
SABC = SABN + SNBC = 2 ⋅ SABN = 2 ⋅ (SAMN + SMBN) = 4t
Resposta: alternativa c.
3. Seja x a medida do lado do quadrado menor e y, a do maior.
Então:
0,48x2 = 0,27y2 ⇒ 48x2 = 27y2 ⇒ ⇒
Resposta: alternativa a.
4. Considerando as informações do enunciado, obtém-se o retângulo a seguir:
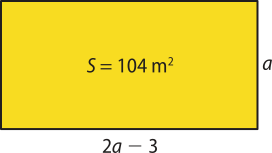
S = (2a − 3)a ⇒ 104 = 2a2 − 3a ⇒ 2a2 − 3a − 104 = 0
Resolvendo a equação do 2º grau, obtêm-se as raízes a(minutos)" = −6,5 e a(segundos)" = 8.
Como a representa o lado de um polígono, então deve-se desconsiderar a solução negativa.
2a − 3 = 2 ⋅ 8 − 3 = 13
A medida do comprimento é 13 m e, portanto: 12 m < 13 m < 14 m Resposta: alternativa b.
5. Pode-se representar a situação por meio da seguinte figura:
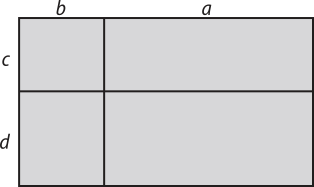
Sabe-se quê: ac = 9; bc = 3; bd = 8.
Assim, obtém-se: a = 3b e d = .
A área S da sala será dada pelo produto entre a e d.
S = 3b ⋅ = 24
Portanto, a área total é 44 m2, pois 24 + 9 + 8 + 3 = 44.
Resposta: alternativa c.
6. Considerando os dados do enunciado, pode-se concluir quê R e H, em km2, são dados por:
R = 1,5 ⋅ 3 = 4,5 ⇒ R = 4,5
⇒ ⇒ H = = 2,5
Soma das áreas, em km2, é: R + H = 4,5 + 2,5 = 7.
Como 1 km2 equivale a 106 m2, então 7 km2 equivale a 7 ⋅ 106 m2.
Portanto:
![]() ⇒ y = = 7 ⋅ 102 = 700
⇒ y = = 7 ⋅ 102 = 700
Como com 1 hectare de cana é possível produzir 8.000 litros de etanol, então com 700 hectares será possível produzir 5.600.000 litros (700 ⋅ 8.000), ou seja, 5,6 ⋅ 106 litros de etanol.
Resposta: alternativa d.
7. A área do quadrado FGLM é igual à área do paralelogramo HILM, pois ambos compartilham a base e a altura Como o triângulo MKL é comum ao quadrado e ao paralelogramo, então a área da região 1 equivale à da região 2. Dessa maneira, Miguel usaria de sua tinta para pintar as duas regiões e sobraria .
Resposta: alternativa d.
8. A área S da região vermelha, em cm2, é:
S = ( ⋅ (pi)" ⋅32 + ⋅ (pi)" ⋅ (42 − 32)) =
O raio r procurado, em cm, é igual a: (pi)"r2 = r = .
Resposta: alternativa a.
9. Como o mássimo quê o dono da loja pagará por cartão é R$ 0,80, a maior área possível para cada cartão é 80 cm2. Considere as seguintes áreas, em cm2:
Striângulo = ≃ 61, 2
Squadrado = 82 = 64
Sretângulo = (11 ⋅ 8) = 88
Shekzágono = ≃ 91, 8
Scírculo = (pi)" ⋅ ≃ 75
Logo, a maior área útil de cartão disponível pelo custo de até R$ 0,80 é o modelo cuja face útil para impressão corresponde ao formato de um círculo de diâmetro 10 cm.
Resposta: alternativa e.
10. Considerando (éli)" como a medida do lado do hekzágono ABCDEF, a medida do apótema m será: m = (éli)" ⋅ .
Portanto, a medida x do lado do hekzágono GHIJKL será: x = (éli)" ⋅
Assim: .
Resposta: alternativa e.
11. Para calcular a medida EF, podemos considerar os triângulos semelhantes APF e ABC. Assim, temos:
⇒ ⇒ ⇒ EF =
A área A(x) de ADEF é:
A(x) = = 8x −
Assim, A(x) = 8x − para 0 ≤ x ≤ 12.
Resposta: alternativa d.
12. Considere x e L os catetos do triângulo retângulo de hipotenusa 2, conforme mostra a figura.
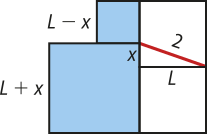
Pelo teorema de Pitágoras, temos:
x2 + L2 = 22 ⇒ x2 + L2 = 4
A soma S das áreas dos quadrados azuis é dada por:
S = (L + x)2 + (L − x)2 = 2(L2 + x2) = 2 ⋅ 4 = 8
Resposta: alternativa d.
Página trezentos e noventa e sete
13. Seja x a medida do lado de cada quadradinho da malha, a área do polígono amarelo é dada pela soma das áreas dos triângulos ABC e BDE.
Logo:
= 30 ⇒ x2 = 6
Resposta: alternativa e.
14. Considere x e y as dimensões reais do parque. Então:
x = 2 ⋅ 5.000 = 100
y = 8 ⋅ 5.000 = 400
A área real, em m2, é: 100 ⋅ 400 = 40.000.
Resposta: alternativa a.
15. (12 − x) ⋅ 1,5 ≥ 72 ⇒ x ≤ −36
Resposta: alternativa d.
16. a) Note quê x > 0, pois é o comprimento da base , e x ≤ 24 por estar sobre a base do retângulo R. Além díssu, para 0 < x ≤ 24, a altura do triângulo é menor ou igual a altura do retângulo. Logo, a construção póde sêr realizada para 0 < x ≤ 24.
b) Como BC = pelo teorema de Pitágoras, temos:
AC2 = x2 + ⇒ AC =
c) A área do triângulo ABC é igual a 64, quando:
= 64 ⇒ x = 16
17. Como N é ponto médio de a distância de N até a reta suporte do lado é , mêtáde da altura h do trapézio, como mostra a figura. Além díssu, é também a altura do triângulo BMN relativa à base . Assim, pela área do triângulo BMN, temos:
= 1 ⇒ h = 8
Portanto, a área S do trapézio é:
S = = 24
Portanto, a área do trapézio é 24 u.a.
Resposta: alternativa d.
18. A diferença entre as áreas das duas pitssas é, em cm2:
402 − 3,14 ⋅ 202 = 344
Resposta: alternativa c.
19. A área B da região em branco, em cm2, é: B = 12 ⋅ 10 − 58 = 62.
A área H da região hachurada, em cm2, é: H = 13 ⋅ 11 − 62 = 81.
Resposta: alternativa e.
20. Seja x o número mássimo de alunos quê satisfaz as condições do enunciado: x = = 32.
Resposta: alternativa c.
21. Pela lei dos cossenos, temos:
y2 = x2 + (4 − x)2 − 2 ⋅ x ⋅ (4 − x) ⋅ cos 60°
y2 = 3x2 − 12x + 16
A área A(x) do triângulo DEF é:
A(x) = (3x2 − 12x + 16)
Resposta: alternativa e.
Capítulo 8 • Geometria Espacial de Posição
Atividades
1. Completando as lacunas, obtém-se:
I. Dois pontos distintos determinam uma única reta. (Pelo postulado R2.)
II. Em um plano, estão contidas infinitas retas. (Pelo postulado P1.)
III. Uma reta em um plano divide-o em duas regiões, denominadas semiplanos. (Pelo postulado P4.)
IV. Por uma reta passam infinitos planos. (Pelo postulado P6.)
V. Pode-se determinar um plano de quatro maneiras. (Pelo postulado P3 e pêlos teoremas 1, 2 e 3 apresentados.)
Ordem das palavras quê preenchem as lacunas: dois – infinitas – semiplanos – infinitos – quatro Resposta: alternativa c.
2. Três retas distintas, duas a duas paralelas entre si, determinam um plano caso as retas sêjam coplanares, ou três planos, se as retas não forem coplanares.
3. Sejam A, B, C e D os pontos. Tem-se três casos: Se A, B, C, D são colineares, eles não determinam um plano. Se A, B, C, D são coplanares, eles determinam um único plano. Se ABC, ABD, ACD e BCD são quatro planos (três pontos não colineares sempre determinam um plano), então tem-se quatro planos.
4. Considerando as definições, têm-se as possíveis respostas:
a) Uma resposta possível: e .
b) Uma resposta possível: e .
c) Uma resposta possível: e e .
d) Uma resposta possível: e e .
5. a) Segundo o enunciado, tem-se
b) Falsa. Segundo o postulado R2, pelo ponto de intersecção da reta r com o plano e o ponto M passa apenas uma reta, definida por esses pontos.
6. Considerando a ilustração do enunciado, conclui-se:
a) é secante ao plano ABC, sêndo o ponto B a intersecção entre eles.
b) está contida no plano FGH.
• Resposta pessoal. Exemplo de pergunta: Qual é a posição relativa da reta em relação aos planos ABE e CGF?
A reta é a intersecção entre os dois planos, ou seja, está contida nos planos ABE e CGF.
Página trezentos e noventa e oito
7. Considerando a ilustração do enunciado, conclui-se:
a) Os planos VAB e VBC são secantes, sêndo a reta a intersecção entre eles.
b) A reta é a intersecção entre os planos ABC e VBC.
c) Não há planos paralelos na figura.
8. 01) Incorreta. No espaço, duas retas podem sêr paralelas (distintas ou coincidentes), concorrentes (perpendiculares ou oblíquas) ou reversas.
02) Incorreta. Para quê um ponto e uma reta determinem um único plano, é necessário quê o ponto não pertença à reta.
04) Correta. Há infinitos planos concorrentes cuja intersecção é uma reta dada.
08) Correta. Se uma reta tem um único ponto em comum com dois planos distintos, então esses dois planos não são paralelos, sêndo, portanto, secantes.
16) Incorreta. Para quê três pontos distintos determinem um plano, eles não podem sêr colineares.
Logo, são corretas as alternativas 04 e 08.
9. Cada aresta lateral da pirâmide é reversa a exatamente 4 arestas da base (aquelas quê não compartilham extremidade com a aresta lateral) e não é reversa a nenhuma outra aresta lateral (pois têm o vértice da pirâmide como intersecção). Como há 6 arestas laterais, a quantidade de pares de arestas reversas na pirâmide é igual a: 6 ⋅ 4 = 24.
Resposta: alternativa b.
10. a) Incorreta. A reta s póde estar contida no plano (alfa)" ou sêr paralela a ele.
b) Incorreta. Segundo o enunciado, a reta t é secante ao plano (beta)", logo a interseção entre t e (beta)" não é vazia.
c) Incorreta. Como o ponto P pertence à reta r e a reta r está contida no plano (alfa)", temos quê P pertence a (alfa)".
d) Correta. Como o ponto P pertence à reta r e, também, à reta t, temos quê a intersecção entre essas retas não é vazia (r ∩ t = {P}).
Resposta: alternativa d.
11. Considerando as informações do enunciado, conclui-se:
a) Uma resposta possível: .
b) Resposta esperada: Sim, o teorema 6 garante quê a reta é paralela ao plano quê contém o hekzágono PQRSTU.
c) Resposta esperada: O teorema 7 garante quê os planos
BCRQ e EFUT são paralelos.
12. a) Verdadeira. Essa afirmação decorre dos teoremas 5 e 7.
b) Falsa. Podem-se conduzir infinitos planos, sêndo apenas um deles paralelo ao plano dado.
c) Falsa. As retas, sêndo reversas, estão contidas em planos distintos.
d) Falsa. Existem retas paralelas a dois planos concorrentes.
e) Falsa. Dois planos podem sêr secantes, paralelos ou coincidentes.
Resposta: alternativa a.
13. a) Incorreta. As retas e são perpendiculares entre si, pois elas se cruzam, formando um ângulo reto.
b) Correta. A reta não intersecta o plano (ADH); logo, a reta é paralela ao plano (ADH).
c) Incorreta. As retas e são reversas.
d) Incorreta. A reta é paralela ao plano (EFG).
e) Incorreta. As retas e são paralelas entre si.
Resposta: alternativa b.
14. Analisando cada alternativa, conclui-se:
I. Falsa. Qualquer reta contida em um dos planos, distinta da intersecção e paralela a ela, não estará contida no outro plano.
II. Falsa. As retas podem sêr paralelas a dois planos secantes.
III. Verdadeira.
IV. Verdadeira.
V. Falsa. póde sêr reversa.
As sentenças falsas são I, II e V.
Resposta: alternativa b.
15. Considerando a figura do enunciado, conclui-se quê:
a) r é paralela a s; s é perpendicular a t; x é reversa a r; y é reversa a t.
b) A reta t é paralela ao plano (alfa)" e a reta r é secante ao plano (beta)".
16. De acôr-do com a figura do enunciado, a posição em cada item é:
a) Perpendiculares, pois são lados adjacentes da mesma face do cubo.
b) Reversas ortogonais, pois é paralela a , quê é perpendicular a . Além díssu, as retas e não possuem pontos em comum e estão contidas em planos distintos.
17. I. Falsa. As retas podem sêr paralelas distintas.
II. Falsa. Se as retas r e s forem reversas, os triângulos não serão coplanares.
III. Verdadeira.
Resposta: alternativa c.
18.
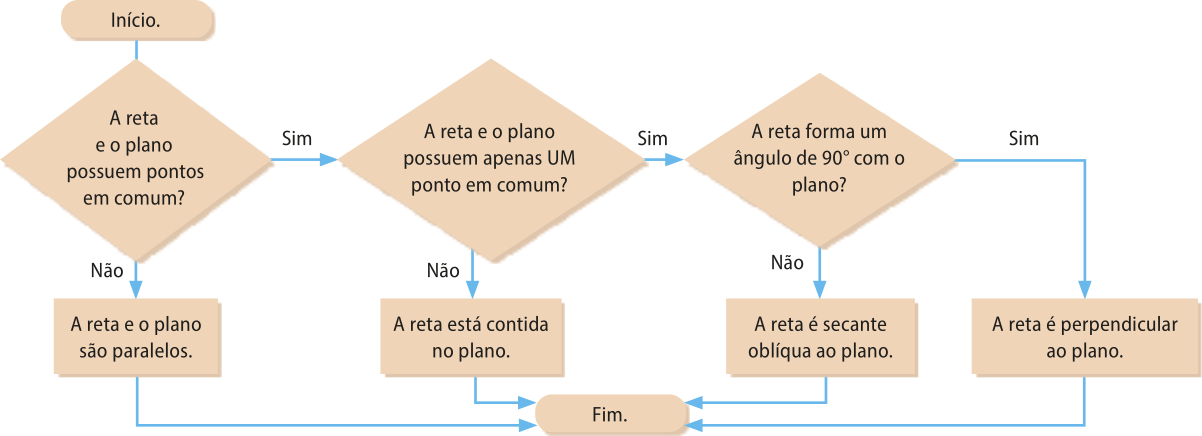
Página trezentos e noventa e nove
19.
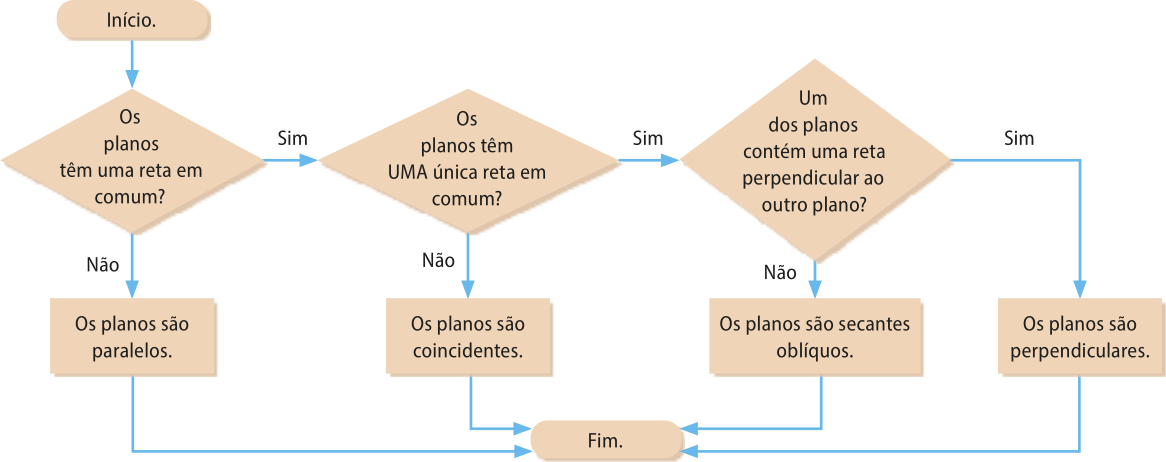
20. I. Verdadeira.
II. Falsa, pois as retas r e s podem sêr reversas.
III. Falsa, pois a reta póde sêr ortogonal a uma reta do plano.
Resposta: alternativa e.
21. a) Falsa. Observe a ilustração a seguir.
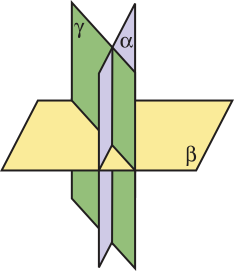
Temos (gama)" ⊥ (beta)", mas (gama)" e (beta)" são secantes a (alfa)".
b) Falsa. A reta póde sêr paralela aos dois planos.
c) Falsa. Elas podem sêr concorrentes ou também podem sêr reversas, se pertencerem a planos distintos.
d) Falsa. Considerando o cubo representado a seguir.
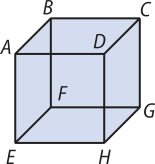
é ortogonal a , e é ortogonal a , mas não é paralela a
e) Verdadeira. Considerando o cubo representado a seguir.
Retas paralelas a : , (são perpendiculares ou ortogonais a ).
Resposta: alternativa e.
22. Como o plano (beta)" é perpendicular ao plano (alfa)", a projeção de um conjunto de pontos de (beta)" em (alfa)" será representada por um único ponto ou um segmento de reta. No caso da projeção de um polígono em (beta)", quê é formado por segmentos de reta não colineares, sua projeção será um segmento de reta.
23. a) A projeção ortogonal do ponto G sobre o plano ABC é o ponto C.
b) A projeção ortogonal do ponto A sobre o plano BCF é o ponto B.
c) A projeção ortogonal do ponto V1 sobre o plano ABC é o ponto V2.
24. A projeção do segmento no solo é o segmento pois o ponto C e o ponto E são as projeções ortogonais no plano do solo referentes ao ponto A e ao ponto B, respectivamente.
Resposta: alternativa d.
25. Ao projetar no plano (alfa)" as trajetórias presentes na linha do equador, essas projeções serão curvas, enquanto ao projetar as trajetórias realizadas nos meridianos 1 e 2, essas projeções serão linhas retas.
Resposta: alternativa e.
26. a) Na projeção do elemento suspenso sobre o piso, apenas a largura e o comprimento são relevantes.
b) A projeção do elemento suspenso sobre o piso é um retângulo de dimensões 0,55 m e 0,25 m. Sua área é, em métro quadrado: (0,55 m) ⋅ (0,25 m) = 0,1375.
c) O retângulo exterior ao piso tátil tem comprimento, em métro:
(0,60 + 0,55 + 0,60) = 1,75.
O retângulo exterior ao piso tátil tem largura, em métro:
(0,60 + 0,25 + 0,60) = 1,45.
O retângulo exterior ao piso tátil tem perímetro, em métro:
2 ⋅ (1,75 + 1,45) m = 6,4.
27. a) Aplicando o teorema de Pitágoras ao triângulo CDH, obtemos:
CH2 = cê dê2 + DH2 ⇒ CH2 = 122 + 52 ⇒ CH = ±13
Como CH é a medida de uma distância, desconsidera-se o valor negativo e, assim, a distância entre os pontos C e H é igual a 13 cm.
b) A distância, em cm, entre o ponto D e a reta é d = DA = 4.
c) A distância, em cm, entre o ponto F e o plano ADH é d = FE = 12.
d) A distância, em cm, entre as retas reversas e é d = FG = 4.
e) A distância, em cm, entre as retas paralelas e é d = CH = 13.
f) A distância, em cm, entre a reta e o plano CDG é d = BC = 4.
g) A distância, em cm, entre os planos paralelos ABC e EFG é d = AE = 5.
28. Tanto a distância de Q ao plano (beta)" quanto a distância dos pontos de r ao plano (beta)" coincidem com a distância entre os planos (alfa)" e (beta)", sêndo, portanto, essas distâncias iguais.
Resposta: alternativa c.
Página quatrocentos
29. Aplicando o teorema de Pitágoras ao triângulo retângulo PQP(minutos)", obtemos: (PQ)2 = (PP(minutos)")2 + (QP(minutos)")2 ⇒ ()2 = 82 + (QP(minutos)")2 ⇒ QP(minutos)" = ± 5. Como QP(minutos)" é a medida de uma distância, desconsidera-se o valor negativo e, assim, a distância entre os pontos P(minutos)" e Q é 5 cm.
Resposta: alternativa b.
30. Aplicando o teorema de Pitágoras no triângulo retângulo ABC, obtemos: AC2 = AB2 + BC2 ⇒ AC2 = 62 + 242 = 612.
Aplicando o teorema de Pitágoras no triângulo retângulo ACD, obtemos: cê dê2 = AD2 + AC2 ⇒ cê dê2 = 82 + 612 ⇒ cê dê = 26
Portanto: cê dê = 26 cm.
Resposta: alternativa a.
31. Como a área do quadrado ABCD é 10 cm2, a medida do lado dêêsse quadrado é (éli)" = cm.
A medida da diagonal do quadrado ABCD é . Logo:
AC = ( cm) ⋅ ⇒ AC = cm.
Aplicando o teorema de Pitágoras no triângulo retângulo ACP, obtemos: AP2 = AC2 + CP2 ⇒ AP2 = + 42 ⇒ AP = ± 6.
Como AP é a medida de uma distância, desconsidera-se o valor negativo e, assim, a distância entre P e a A é igual a 6 cm.
Resposta: alternativa a.
Atividades complementares
1. a) Verdadeira, pois três pontos distintos em uma circunferência são não colineares.
b) Verdadeira, pois os três pontos são colineares.
c) Verdadeira, pois estão contidos em duas retas concorrentes.
d) Falsa, um plano póde conter apenas uma reta secante à circunferência.
e) Verdadeira, pelo postulado de Euclides ou postulado das paralelas.
Resposta: alternativa d.
2. a) Falsa, pois .
b) Falsa, pois .
c) Falsa, pois é concorrente com , quê por sua vez também é concorrente com .
d) Falsa, pois .
e) Verdadeira.
Resposta: alternativa e.
3. A partir do enunciado, obtém-se:
Qualquer reta de (alfa)" é concorrente ou reversa a s.
Resposta: alternativa e.
4. a) Falsa, pois podem sêr determinados infinitos planos cuja intersecção é uma única reta dada.
b) Falsa. Se as retas forem coincidentes podem-se determinar infinitos planos.
c) Falsa, pois, se os três pontos forem colineares, determina-se uma reta e, assim, infinitos planos quê a contêm.
d) Verdadeira.
e) Falso, pois, como o ponto pertence à reta, tem-se como referência apenas a reta, portanto determinam-se infinitos planos quê a contêm.
Resposta: alternativa d.
5. Pode-se considerar o cubo representado a seguir. Considerando a aresta contida na reta suporte r e a aresta contida na reta suporte s, pode-se considerar quê o lado estará contido na reta suporte t, ou seja, a reta quê é uma perpendicular comum a r e a s.
Portanto, t é a reta suporte de uma aresta do cubo.
Resposta: alternativa c.
6. Como a escada é circular, então o corrimão também será circular. Os cinco pontos A, B, C, D e E sobre o corrimão estão igualmente espaçados. Além díssu, A, P e E pertencem a uma mesma reta.
Como na escada a pessoa caminha deslizando a mão sobre o corrimão do ponto A até o ponto D, aproximadamente, da circunferência, a alternativa c é a quê melhor representa a projeção ortogonal sobre o piso da casa (plano) do caminho percorrido pela mão dessa pessoa.
Resposta: alternativa c.
7. a) Incorreta. Caso os pontos sêjam colineares, os planos podem sêr secantes.
b) Incorreta. Os planos (alfa)" e (beta)" podem sêr secantes.
c) Incorreta. Se dois planos distintos são perpendiculares a uma mesma reta, então eles são paralelos e não possuem nenhum ponto em comum.
d) Correta. De fato, se duas retas são perpendiculares a um plano, então elas são paralelas entre si.
e) Incorreta. Toda reta paralela a um plano é necessariamente paralela ou reversa às retas dêêsse plano.
Resposta: alternativa d.
8. a) Incorreta. A reta r póde estar contida em (beta)".
b) Incorreta. Se a projeção ortogonal da reta r no plano (beta)" não tiver um ponto em comum à reta s, então r e s são reversas.
c) Correta. As retas r e s podem sêr concorrentes ou reversas.
d) Incorreta. A reta s póde também estar contida em um plano paralelo ao plano (alfa)".
e) Incorreta. A reta r póde estar contida em (beta)" e sêr perpendicular à reta s.
Resposta: alternativa c.
9. A projeção de A até B será um arco da circunferência e a projeção de B até C será um segmento de reta.
Resposta: alternativa e.
10. As projeções ortogonais das lêtras serão retangulares de mesma largura, com espaçamento idênticos entre elas. A de maior comprimento é correspondente à letra N. As com os comprimentos praticamente de mesmas medidas são correspondentes às lêtras P e E. A de menor comprimento será o da letra I.
Resposta: alternativa e.
11. Pela vista superior, sabemos quê a torre tem o formato circular, pois são ilustrados três círculos concêntricos. Pelas vistas frontal e de perfil, sabemos quê o círculo maior da torre é a sua base, o círculo do meio é a sua parte superior e o menor círculo indica quê a torre possui um furo interno na forma de um cilindro.
Resposta: alternativa e.
12. A projeção do caminho de A até B é um segmento de reta; a projeção do arco circular BCD é um arco congruente ao arco BCD; a projeção do caminho de D até E é um segmento de reta de modo quê os pontos A, B, D e E sêjam colineares.
Resposta: alternativa c.
13. As alternativas a e b possuem projeções ortogonais não alinhadas na malha quadriculada. A projeção ortogonal da vista frontal na alternativa c está errada, e a projeção ortogonal no plano do chão da alternativa d está errada.
Resposta: alternativa e.
14. O telhado da casa da figura 2 possui quedas para as laterais e uma queda para a frente da casa, e a sua projeção ortogonal no plano do chão será um retângulo.
Resposta: alternativa b.
1 BRASIL. Ministério da Educação. Base Nacional Comum Curricular: educação é a base. Brasília, DF: MÉC, 2018. p. 462. Disponível em: https://livro.pw/asnqu. Acesso em: 11 set. 2024.