CAPÍTULO 3
CORPOS REDONDOS
Os silos são estruturas fundamentais na armazenagem de grãos e produtos agrícolas, em razão de sua eficiência e praticidade. Sua forma é escolhida por diversos motivos técnicos e práticos: ela oferece uma distribuição uniforme da pressão, prevenindo a compactação e a deterioração dos grãos; torna os silos mais resistentes a forças externas, como ventos e tempestades, proporcionando estabilidade; e garante eficiência espacial e simplificação da manutenção.
Em termos de eficiência espacial, o formato cilíndrico dos silos maximiza a capacidade de armazenamento quando comparado a silos de outros formatos com mesma área de superfícíe. Além díssu, sua estrutura simplifica a manutenção, por facilitar a limpeza e por reduzir os custos operacionais, especialmente durante o escoamento de grãos, uma vez quê é comum quê os silos não possuam canos para captação ou retirada dos produtos armazenados e quê o escoamento ocorra devido à ação da gravidade.
Muitos silos não são unicamente cilíndricos, e seu formato se apresenta como uma junção de formas arredondá-das; esse é o caso dos silos da imagem, quê lembram cones acoplados a cilindros. Esses são dois dos corpos redondos quê estudaremos neste Capítulo.
Fonte dos dados: SONEGO, Giseli V. As contribuições da etnomodelagem matemática no estudo da geometria espacial. 2009. Dissertação (Mestrado Profissionalizante em Ensino de Física e de Matemática) – Centro Universitário Franciscano de Santa Maria, Santa Maria, 2009. Disponível em: https://livro.pw/vsvpk. Acesso em: 3 nov. 2024.
Página noventa e um
![]() Agora, reúna-se a um colega, e façam o quê se pede em cada questão.
Agora, reúna-se a um colega, e façam o quê se pede em cada questão.
1. De acôr-do com o texto, quais são as vantagens do formato cilíndrico dos silos?
2. Pesquisem outros formatos e tipos de silos.
3. Citem exemplos de elemêntos do cotidiano com formatos arredondá-dos.
4. Com base em seus conhecimentos, expliquem como determinar o volume de um cilindro reto.
Ver as Orientações para o professor.

Página noventa e dois
Introdução
No Capítulo anterior, estudamos os sólidos geométricos chamados de poliedros. Neste Capítulo, iremos estudar alguns dos sólidos geométricos quê têm pelo menos uma parte de sua superfícíe curva e são denominados corpos redondos: cilindro, cone e esféra.
Diversos objetos quê utilizamos no dia a dia apresentam formas arredondá-das, como copos, panelas, entre outros. Na arquitetura, também observamos formas arredondá-das, presentes em diversas construções. Na indústria, os tanques de gás natural têm o formato esférico, modelo mais recomendado para esse tipo de produto.



Página noventa e três
Cilindro
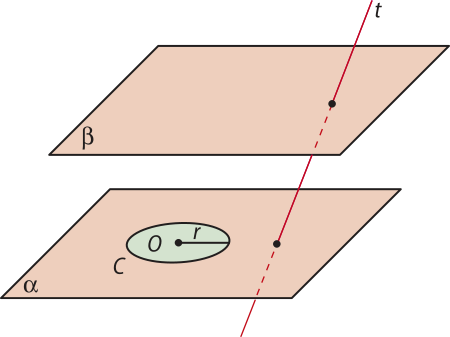
Vamos considerar dois planos paralelos (alfa)" e (beta)", um círculo C de centro O e raio r contido em (alfa)" e uma reta t secante aos planos (alfa)" e (beta)".
A figura geométrica formada pela reunião de todos os segmentos de reta paralelos à reta t com uma extremidade em um ponto do círculo C e a outra no plano (beta)" é denominada cilindro circular ou simplesmente cilindro.
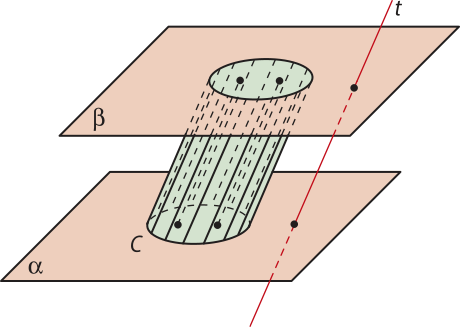
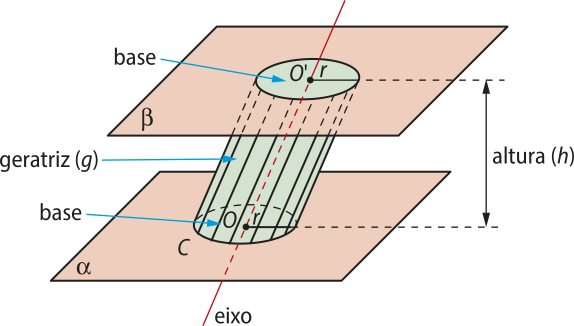
Considerando o cilindro representado na figura a seguir, destacamos os seguintes elemêntos:
• Bases: são os círculos de raio r e centros O e O’, situados nos planos paralelos (alfa)" e (beta)", respectivamente;
• Altura: é a distância entre os planos paralelos (alfa)" e (beta)", cuja medida indicaremos por h;
• Eixo: é a reta , quê contém os centros das bases;
• Geratrizes: são os segmentos de reta paralelos ao eixo e cujas extremidades são pontos das circunferências das bases; indicaremos suas medidas por g.
De acôr-do com a inclinação do eixo em relação aos planos das bases, os cilindros podem sêr oblíqüos ou rétos.
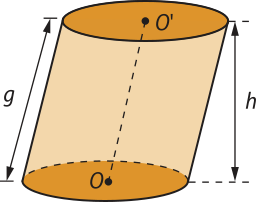
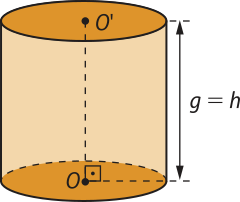
Um cilindro é oblíquo quando o eixo é oblíquo aos planos das bases e é reto quando o eixo é perpendicular aos planos das bases.
Página noventa e quatro
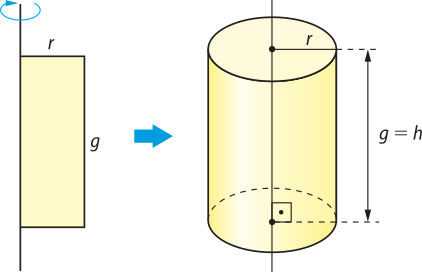
Um cilindro reto também póde sêr obtído pela rotação completa de um retângulo em torno da reta suporte de um de seus lados. Assim, o cilindro reto também é denominado cilindro de revolução.
Secções de um cilindro
A secção ôbitída pela intersecção de um cilindro com um plano paralelo às suas bases é denominada secção transversal do cilindro.
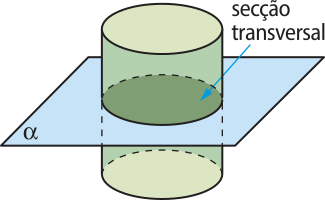
Pense e responda
Observe a imagem e responda: qual figura geométrica plana é determinada pela secção transversal do cilindro?
A secção transversal é um círculo congruente às bases do cilindro.
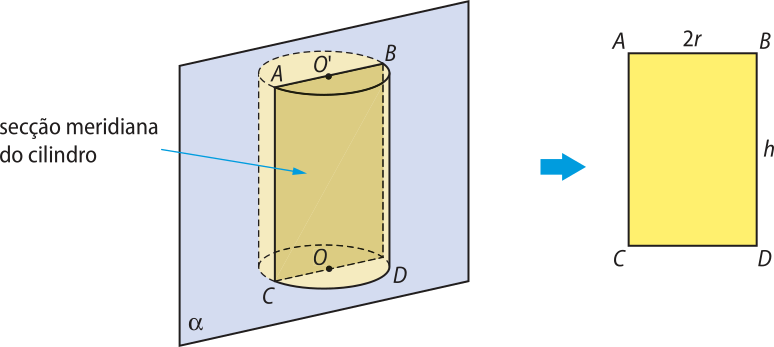
A secção ôbitída pela intersecção de um cilindro com um plano quê contém seu eixo é denominada secção meridiana do cilindro.
A secção meridiana de um cilindro reto é um retângulo de dimensões 2r (medida do diâmetro das bases do cilindro) e h (altura do cilindro).
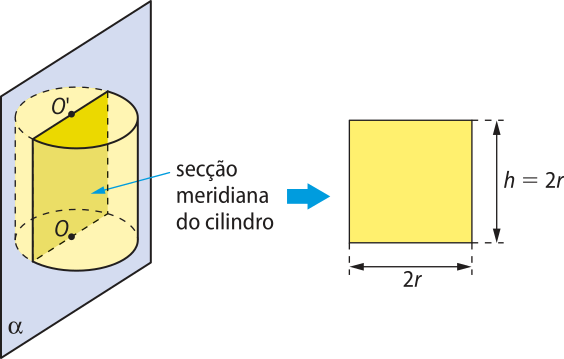
Se a altura do cilindro reto for igual à medida do diâmetro da base, ou seja, h = 2r, então a secção meridiana é um quadrado, e o cilindro é chamado de cilindro equilátero.
Página noventa e cinco
Área da superfícíe de um cilindro reto
Vamos planificar a superfícíe de um cilindro reto de altura h e raio da base r para determinar a área da sua superfícíe.
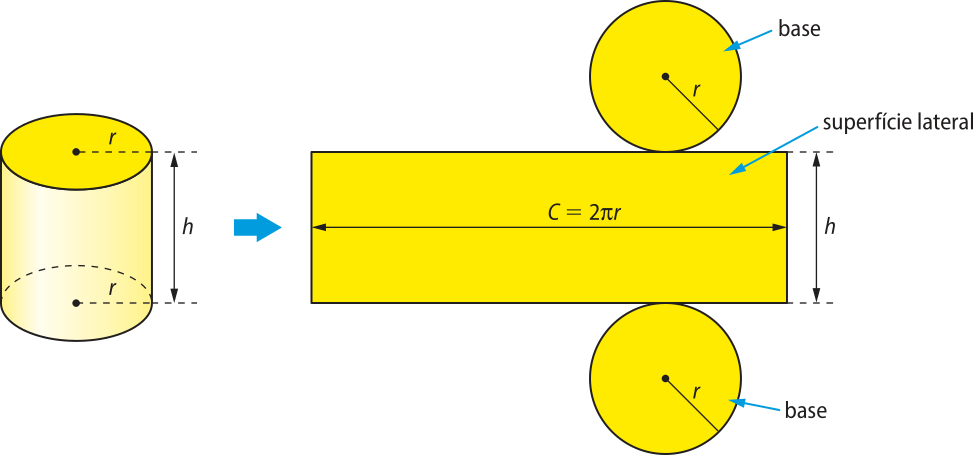
A superfícíe total de um cilindro reto é formada pela superfícíe lateral e pela superfícíe das duas bases circulares. Como podemos observar pela planificação, a área dessa superfícíe é a área do retângulo de dimensões 2(pi)"r e h mais as áreas das bases, cada uma delas equivalente à área de um círculo de raio r.
Assim, temos:
• área lateral (S(éli)"): S(éli)" = 2(pi)"rh
• área da base (Sb): Sb = (pi)"r2
• área total (St): St = S(éli)" + 2Sb
Volume de um cilindro
Considere a situação a seguir.
Em um treinamento do Corpo de Bombeiros, uma mangueira acoplada a um caminhão foi esticada e completamente preenchida com á gua para testes, formando um cilindro reto. Para o planejamento de futuras ações, deseja-se saber o volume de á gua necessário para preencher o interior dessa mangueira.
Para responder a kestões como essa, é necessário calcular o volume do cilindro, o quê estudaremos a seguir.

Página noventa e seis
Considere um cilindro e um prisma com mesma altura h e bases de áreas iguais a Sb contidas em um plano (alfa)".
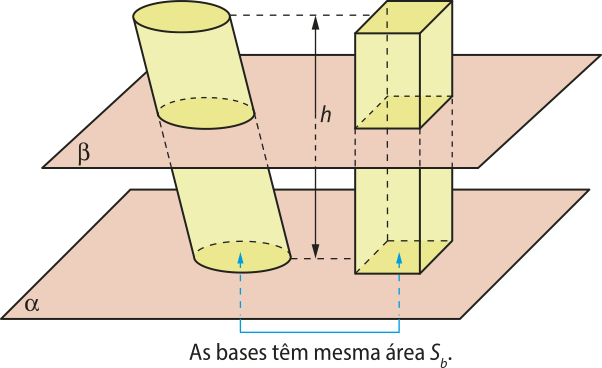
Qualquer plano (beta)" paralelo ao plano (alfa)" quê intersecte os dois sólidos determina neles secções transversais congruentes às respectivas bases. Como as áreas das bases do cilindro e do prisma são iguais e valem Sb, então as secções transversais também têm área igual a Sb.
Portanto, pelo princípio de Cavalieri, concluímos quê o volume do cilindro é igual ao volume do prisma.

Como o volume do prisma é dado pelo produto da área da base pela altura, então o volume do cilindro também será calculado da mesma maneira. Assim, podemos escrever:
volume do cilindro = (área da base) ⋅ (altura)
Em um cilindro cuja base tem raio r, a área da base é dada por Sb = (pi)"r2. Portanto, se a altura do cilindro é h, seu volume é dado por:
V = (pi)"r2h
Note quê esse resultado é válido tanto para cilindros oblíqüos quanto rétos.
ATIVIDADES RESOLVIDAS
1. Uma lata cilíndrica e reta tem as medidas indicadas na figura.
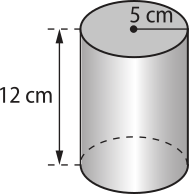
Nessas condições, e adotando (pi)" = 3,14, responda:
a) Qual é a quantidade mínima de papel, em cm2, necessária para cobrir a superfícíe lateral dessa lata?
b) Qual é a área total da superfícíe dessa lata?
c) Quantos mililitros (mL) de líquido cabem nessa lata?
Resolução
Planificando a superfícíe do cilindro, temos:
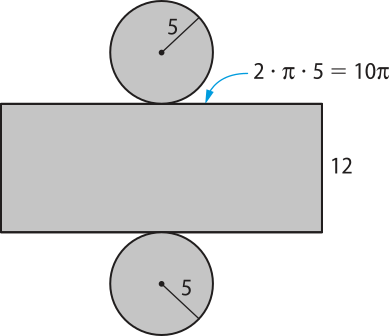
a) Área lateral (S(éli)"), em cm2:
S(éli)"= 10(pi)" ⋅ 12 = 120(pi)" ⇒ S(éli)" = 120(pi)"
Considerando (pi)" = 3,14, temos:
S(éli)" = 120 ⋅ 3,14 = 376,8
Assim, a quantidade mínima de papel é 376,8 cm2.
Página noventa e sete
b) Área total (St), em cm2:
St = S(éli)" + 2 ⋅ Sb = 376,8 + 2 ∙ ((pi)" ⋅ 52) = 376,8 + 50(pi)" = 376,8 + 50 ⋅ 3,14 = 533,8
Portanto, a área total da superfícíe da lata é 533,8 cm2.
c) O volume V de líquido quê cabe na lata, em cm3, é dado por:
V = (pi)" ⋅ 52 ⋅ 12 ⇒ C = 300(pi)" = 300 ⋅ 3,14 = 942
Como 1 dm3 equivale a 1 L, ou 1 cm3 equivale a 1 mL, temos quê:
942 cm3 = 942 mL
Portanto, cabem 942 mL de líquido na lata.
2. Um líquido quê ocupa uma altura de 10 cm em determinado recipiente cilíndrico será transferido para outro recipiente, também cilíndrico, com diâmetro duas vezes maior do quê o primeiro. Qual será a altura ocupada pelo líquido nesse segundo recipiente?
Resolução
Vamos indicar o volume de líquido no primeiro recipiente por V1 e, no segundo, por V2.
V1 = (pi)"r2h e V2 = (pi)"R2H
Do enunciado, temos: R = 2r e h = 10 cm Como o volume de líquido é o mesmo, temos:
V1 = V2 ⇒ (pi)"r2h = (pi)"(2r)2H
r2h = 4r2H ⇒ H = = 2,5
Portanto, a altura ocupada pelo líquido no segundo recipiente será de 2,5 cm.
3. Calcule a área total do sólido obtído pela rotação completa de um retângulo de dimensões 4 cm e 12 cm em torno do lado:
a) menor;
b) maior.
Resolução
a) O sólido obtído nesse caso é um cilindro reto de raio da base 12 cm e altura 4 cm.
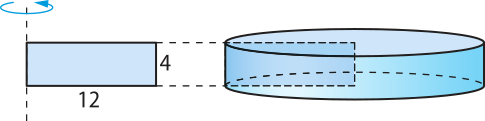
St = S(éli)" + 2 ⋅ Sb ⇒ St = 2(pi)"r ⋅ h + 2 ⋅ (pi)"r2 ⇒ St = 2 ⋅ (pi)" ⋅ 12 ⋅ 4 + 2 ⋅ (pi)" ⋅ 122 ⇒ St = 384(pi)"
Portanto, St = 384(pi)" cm2.
b) O sólido obtído nesse caso é um cilindro reto de raio da base 4 cm e altura 12 cm.
Assim:
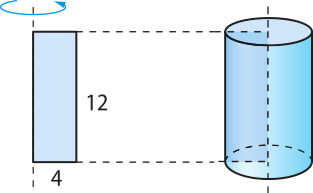
St = 2 ⋅ (pi)" ⋅ 4 ⋅ 12 + 2 ⋅ (pi)" ⋅ 42 ⇒ St = 128(pi)"
Portanto, St = 128(pi)" cm2.
ATIVIDADES
1. Um cilindro reto tem altura igual a 5 cm e raio da base medindo 6 cm. Determine:
a) a área da base;
36(pi)" cm2
b) a área lateral;
60(pi)" cm2
c) a área total.
132(pi)" cm2
2. Determine a área lateral de um cilindro cujo perímetro da base é 62,8 cm e cuja altura é a mêtáde do raio da base. Adote (pi)" = 3,14.
314 cm2
3. A área lateral de um cilindro é 20(pi)" cm2. Se o raio da base méde 5 cm, calcule a altura h dêêsse cilindro.
2 cm
4. Da rotação completa de um retângulo de dimensões 5 cm e 9 cm obtém-se um cilindro reto cuja área da base é 25(pi)" cm2. Calcule a área total dêêsse cilindro.
140(pi)" cm2
5. Quantos centimetros quadrados de uma chapa de metal são necessários para construir uma lata de óleo, com tampa, no formato de um cilindro reto com 8 cm de diâmetro de base e 18 cm de altura?
176(pi)" cm2
Página noventa e oito
6. Em um cilindro equilátero, a área da secção meridiana vale 400 cm2. Calcule:
a) a altura do cilindro;
20 cm
b) a área total da superfícíe do cilindro.
600(pi)" cm2
7. (Enem/MEC) Um povoado com 100 habitantes está passando por uma situação de seca prolongada e os responsáveis pela administração pública local decidem contratar a construção de um reservatório. Ele deverá ter a forma de um cilindro circular reto, cuja base tenha 5 metros de diâmetro interno, e atender à demanda de á gua da população por um período de exatamente sete dias consecutivos. No oitavo dia, o reservatório vazio é completamente reabastecido por carros-pipa.
Considere quê o consumo médio diário por habitante é de 120 litros de á gua. Use 3 como aproximação para (pi)".
Nas condições apresentadas, o reservatório deverá sêr construído com uma altura interna mínima, em métro, igual a
a) 1,12.
b) 3,10.
c) 4,35.
d) 4,48.
e) 5,60.
alternativa d
8. (UEMG) Uma empresa de produtos de limpeza deseja fabricar uma embalagem com tampa para seu produto. Foram apresentados dois tipos de embalagens com volumes iguais. A primeira é um cilindro de raio da base igual a 2 cm e altura igual a 10 cm; e a segunda, um paralelepípedo de dimensões iguais a 4 cm, 5 cm e 6 cm. O métro quadrado do material utilizado na fabricação das embalagens custa R$ 25,00.
Considerando-se (pi)" = 3, o valor da embalagem quê terá o menor custo será:
a) R$ 0,36
b) R$ 0,27
c) R$ 0,54
d) R$ 0,41
alternativa a
9. (Enem/MEC) Um artesão possui pótes cilíndricos de tinta cujas medidas externas são 4 cm de diâmetro e 6 cm de altura. Ele pretende adquirir caixas organizadoras para armazenar seus pótes de tinta, empilhados verticalmente com tampas voltadas para cima, d fórma quê as caixas possam sêr fechadas.
No mercado, existem cinco opções de caixas organizadoras, com tampa, em formato de paralelepípedo reto-retângulo, vendidas pelo mesmo preêço, possuindo as seguintes dimensões internas:
Modelo |
Comprimento (cm) |
Largura (cm) |
Altura (cm) |
|---|---|---|---|
I |
8 |
8 |
40 |
II |
8 |
20 |
14 |
III |
18 |
5 |
35 |
IV |
20 |
12 |
12 |
V |
24 |
8 |
14 |
Qual dêêsses modelos o artesão deve adquirir para conseguir armazenar o maior número de pótes por caixa?
a) I
b) II
c) III
d) IV
e) V
alternativa d
10. (UFRGS-RS) Considere o sólido obtído pela revolução do retângulo ABCD em torno da reta r, conforme indicado na figura a seguir.
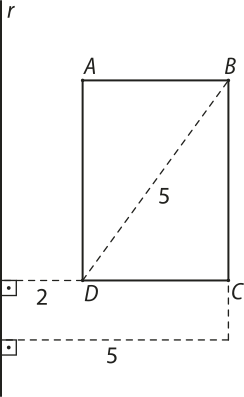
O volume do sólido obtído é
a) 16(pi)".
b) 84.
c) 100.
d) 84(pi)".
e) 100(pi)".
alternativa d
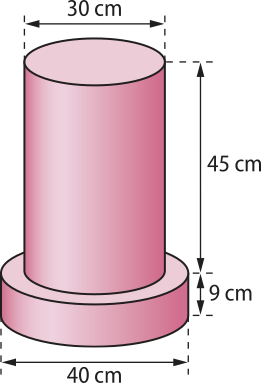
11. Considere um sólido compôzto de dois cilindros rétos, conforme indica a figura. Calcule:
a) a área total da superfícíe dêêsse sólido.
2.510(pi)" cm2
b) o volume total dêêsse sólido.
13.725(pi)" cm3
Página noventa e nove
12. (Enem/MEC) Para resolver o problema de abastecimento de á gua foi decidida, numa reunião do condomínio, a construção de uma nova cistérna. A cistérna atual tem formato cilíndrico, com 3 m de altura e 2 m de diâmetro, e estimou-se quê a nova cistérna deverá comportar 81 m3 de á gua, mantendo o formato cilíndrico e a altura da atual. Após a inauguração da nova cistérna a antiga será desativada.
Utilize 3,0 como aproximação para (pi)".
Qual deve sêr o aumento, em metros, no raio da cistérna para atingir o volume desejado?
a) 0,5
b) 1,0
c) 2,0
d) 3,5
e) 8,0
alternativa c
13. Um cilindro reto tem área lateral de 30(pi)" cm2 e área total de 80(pi)" cm2. Determine seu volume.
75(pi)" cm3
14. (UEG-GO) Em uma festa, um garçom, para servir refrigerante, utilizou uma jarra no formato de um cilindro circular reto. Durante o seu trabalho, percebeu quê com a jarra completamente cheia conseguia encher oito copos de 300 mL cada. Considerando-se quê a altura da jarra é de 30 cm, então a área interna da base dessa jarra, em cm2, é:
a) 10
b) 30
c) 60
d) 80
alternativa d
15. cérto produto de limpeza é vendido em dois recipientes cilíndricos:
(1) lata de raio da base igual a 3,1 cm e altura 11,6 cm;
(2) lata de raio da base igual a 3,1 cm e altura 16,6 cm.
Os preços dêêsse produto são R$ 0,70 e R$ 1,10, respectivamente, para as latas (1) e (2).
Adotando (pi)" = 3,14, faça o quê se pede.
a) Calcule o volume em cada recipiente.
V1 ≃ 350 cm3; V2 ≃ 500 cm3
b) Qual das duas embalagens apresenta melhor preêço para o consumidor?
A lata (1) apresenta melhor preêço para o consumidor.
16. (Ulbra-RS) A Gestão Ambiental visa ao uso de práticas quê garantem a conservação e a preservação da biodiversidade, a reciclagem das matérias-primas e a redução do impacto ambiental das atividades humanas sobre os recursos naturais. Consciente da importânssia de reaproveitar sóbras de madeira, uma serraria quê trabalha apenas com madeira de reflorestamento rêzouvêo calcular a sóbra de madeira na confekissão de peças cilíndricas. Para confeksionar uma peça cilíndrica, a serraria faz os cortes adequados em um prisma quadrangular de arestas da base 5 cm e altura 0,8 m e obtém um cilindro de 5 cm de diâmetro e 0,8 m de altura. A sóbra de madeira na fabricação de mil destas peças é, em cm3 (utilize (pi)" = 3,14), a seguinte:
a) 4,3 ⋅ 10 −5
b) 430
c) 4,3 ⋅ 105
d) 1.570
e) 2.000
alternativa c
17. O sólido de madeira indicado na figura é utilizado para enrolar cabos telefônicos.
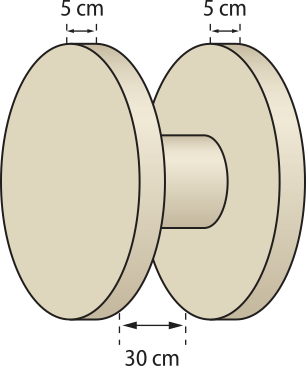
Os cilindros das extremidades e o cilindro interno têm bases com diâmetros de 80 cm e 20 cm, respectivamente. Determine o volume de madeira gasto para construir esse sólido.
19.000(pi)" cm3
18. ![]() É possível construir caixas-d’água cilíndricas usando duas chapas de aço retangulares para revestimento lateral e duas chapas de aço quadradas para as bases. As chapas retangulares são encurvadas e soldadas, e as chapas quadradas são cortadas em círculos inscritos e soldadas. Essas chapas são vendidas por 200 reais o métro quadrado.
É possível construir caixas-d’água cilíndricas usando duas chapas de aço retangulares para revestimento lateral e duas chapas de aço quadradas para as bases. As chapas retangulares são encurvadas e soldadas, e as chapas quadradas são cortadas em círculos inscritos e soldadas. Essas chapas são vendidas por 200 reais o métro quadrado.
Elabore um problema no qual seja necessário determinar o preêço aproximado do gasto com chapas de aço para construir uma caixa-d’água de volume acima de 20 mil litros a partir da altura da caixa-d’água.
Utilize a calculadora para auxiliá-lo nos cálculos.
Resposta pessoal.
Página cem
Cone
Alguns objetos do cotidiano, como funís, casquinhas de sorvete e cones de trânsito, podem sêr associados a um tipo de corpo redondo denominado cone.
Considere um plano (alfa)", um círculo C contido em (alfa)" e um ponto V quê não pertence a (alfa)".
A figura geométrica formada pela reunião de todos os segmentos de reta quê têm uma extremidade no ponto V e a outra em um ponto do círculo C é denominada cone circular ou, simplesmente, cone.
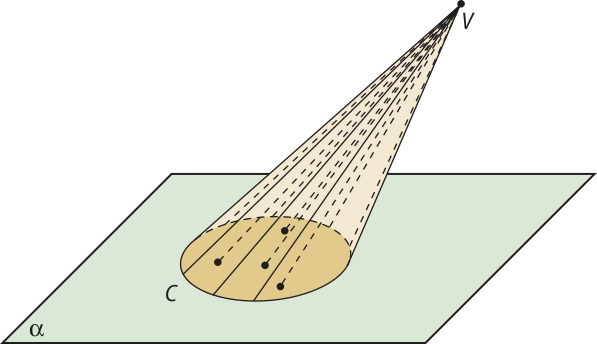
Considerando o cone representado na figura a seguir, destacamos os seguintes elemêntos:
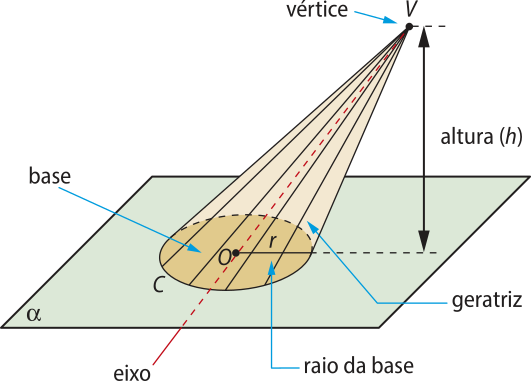
• Base: é o círculo C de raio r e centro O situado no plano (alfa)";
• Vértice: é o ponto V;
• Eixo: é a reta ;
• Altura: é a distância do ponto V ao plano da base, cuja medida indicaremos por h;
• Geratriz: é qualquer segmento de reta cujos extremos são o vértice V e um ponto qualquer da circunferência da base.
De acôr-do com a inclinação de seu eixo em relação ao plano da base, um cone póde sêr oblíquo ou reto. Um cone é oblíquo quando seu eixo é oblíquo ao plano da base e é reto quando seu eixo é perpendicular ao plano da base.
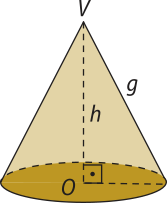
No caso do cone reto, todas as geratrizes têm a mesma medida, usualmente indicada por g.


Página cento e um
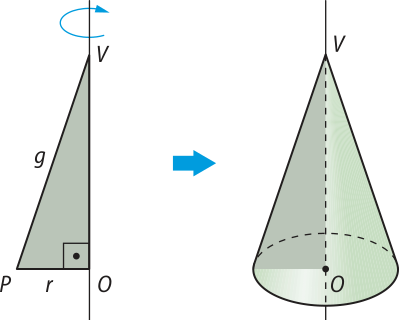
Um cone circular reto também póde sêr obtído pela rotação completa de um triângulo retângulo em torno da reta quê contém um dos catetos. Assim, o cone reto também é denominado cone de revolução.
Secções de um cone
A secção ôbitída pela intersecção de um cone com um plano paralelo à sua base é denominada secção transversal do cone.
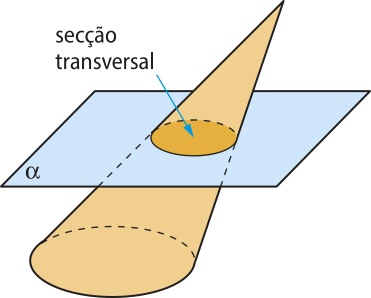
Pense e responda
Qual é a forma geométrica plana determinada por uma secção transversal do cone quê não contém seu vértice?
A secção transversal é um círculo.
A secção ôbitída pela intersecção de um cone com um plano quê contém seu eixo é denominada secção meridiana do cone.
No cone circular reto, a secção meridiana é um triângulo isósceles de base 2r e lados congruentes medindo g (figura 1).
Se a secção meridiana for um triângulo equilátero, ou seja, se g = 2r, o cone é chamado de cone equilátero (figura 2).
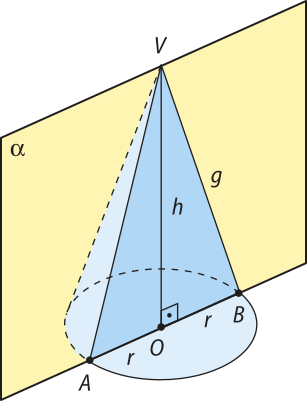
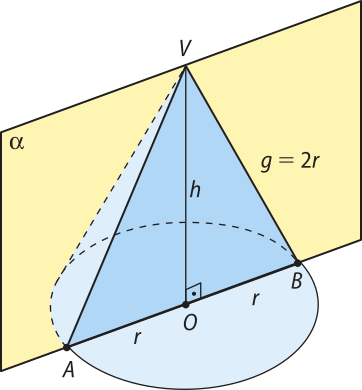
Pense e responda
Observando os cones rétos das figuras 1 e 2, utilize o teorema de Pitágoras no triângulo VOB para determinar uma relação entre as medidas da geratriz g, da altura h e do raio r da base de um cone circular reto.
g2 = h2 + r2
Página cento e dois
Área da superfícíe de um cone reto
Vamos planificar a superfícíe de um cone reto de raio da base r e geratriz g para determinar sua área.
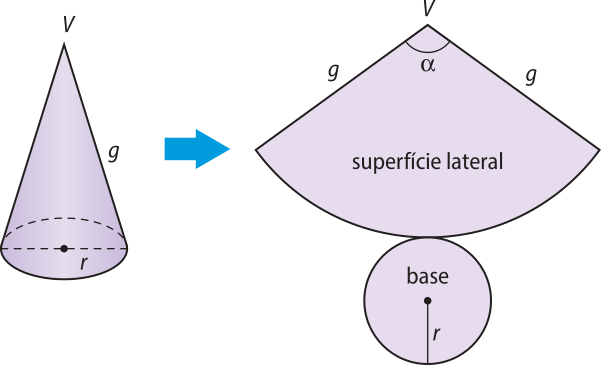
A superfícíe total do cone é formada pela superfícíe da base (círculo) mais a superfícíe lateral (um setor circular). Assim, temos:
• Área lateral (S(éli)"):a área da superfícíe lateral de um cone corresponde à área de um setor circular de raio g (geratriz do cone) e arco de comprimento 2(pi)"r, quê é o comprimento da circunferência da base do cone.
• Área da base (Sb): é a área do círculo de raio r.
Sb = (pi)"r2
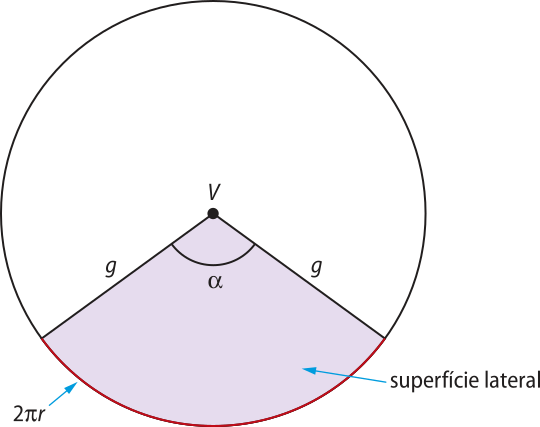
Como a área do setor circular é proporcional ao comprimento do arco correspondente, é possível determinar a área da superfícíe lateral (S(éli)")pela regra de três a seguir:
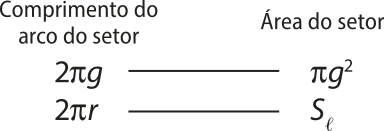
2(pi)"r ⋅ (pi)"g2 = 2(pi)"g ⋅ S(éli)" ⇒ S(éli)" = ![]() ⇒ S(éli)" = (pi)"rg
⇒ S(éli)" = (pi)"rg
• Área total (St): é a soma da área lateral e a da área da base.
St = S(éli)" + Sb
Página cento e três
Volume de um cone
Considere a situação a seguir.
Um doce muito famoso e tradicional no Brasil é o canudinho de doce de leite. Ele consiste em uma massa fina frita em formato quê lembra um cone quê é recheado com doce de leite cremoso. Exatamente por sêr muito famoso, o dono de uma confeitaria decidiu produzir e vender esse doce.
Para determinar quanto doce de leite será necessário fazer, é preciso responder a duas perguntas: quantas unidades de canudinhos ele pretende produzir por dia e qual é a quantidade de doce de leite necessária para preencher cada canudo?

Mas como calcular essa quantidade?
pôdêmos aplicar o princípio de Cavalieri para determinar o volume de um cone a partir do volume de uma pirâmide.
Considere um cone C e uma pirâmide P de mesma altura h e bases de mesma área Sb, contidas em um plano horizontal (alfa)". Qualquer plano (beta)", paralelo ao plano (alfa)", distante h(minutos)" do vértice e secante aos sólidos C e P determina duas secções transversais de áreas S1 e S2, respectivamente.
Sabemos quê, para pirâmides, vale a igualdade . Pode-se provar quê a relação análoga vale também para cones, ou seja, .
Logo, , portanto S1 = S2
.
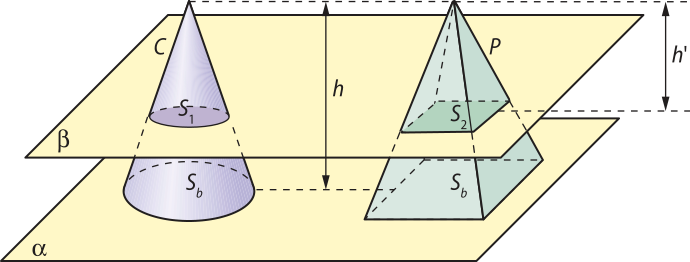
Assim, pelo princípio de Cavalieri, podemos concluir quê o volume da pirâmide P é igual ao volume do cone C e podemos escrever:
Vpirâmide = Vcone =
V = ⋅ Sb ⋅ h ⇒ V = ⋅ (pi)"r2 ⋅ h
Pense e responda
Voltando ao problema do recheio de doce de leite, se o dono da confeitaria fez 800 mL de doce de leite, aproximadamente quantos canudos com 3 cm de diâmetro interno por 8 cm de altura ele poderá preencher? Saiba quê 1 cm3 = 1 mL.
aproximadamente 42 canudos
Página cento e quatro
ATIVIDADES RESOLVIDAS
4. Um fabricante rêzouvêo fazer a embalagem para um de seus produtos no formato de um cone reto, com 8 cm de diâmetro e 12 cm de altura. Qual será a quantidade mínima do material utilizado para cobrir toda a superfícíe dessa embalagem? Use (pi)" = 3,14 e = 3,16.
Resolução
Modelo de embalagem, com medidas em cm:

Aplicando o teorema de Pitágoras, temos:
g2 = 122 + 42 = 144 + 16 = 160
g =
Logo, g = cm.
Vamos agora determinar as áreas em cm2.
Cálculo da área da base (Sb):
Sb = (pi)"r2 = (pi)" ⋅ 42 = 16(pi)"
Cálculo da área lateral (S(éli)"):
S(éli)" = (pi)"rg = (pi)" ⋅ 4 ⋅
Cálculo da área total (St):
St = Sb + S(éli)" = 16(pi)" +
Adotando (pi)" = 3,14 e = 3,16, obtemos:
St = 16 ⋅ (3,14) ⋅ (1 + 3,16) = 50,24 ⋅ (4,16) ≃ 209
Portanto, a quantidade mínima de material será 209 cm2.
5. Em um cone reto, a área da base é 9(pi)" cm2 e a geratriz méde cm. Determine o volume do cone.
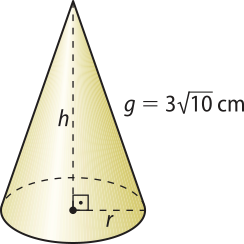
Resolução
Primeiro, vamos determinar o raio da base do cone:
Sb = 9(pi)" ⇒ (pi)"r2 = 9(pi)" ⇒ r2 = 9 ⇒ r = 3
Logo, o raio da base do cone é 3 cm.
Agora, vamos calcular a altura do cone utilizando o teorema de Pitágoras:
g2 = r2 + h2 ⇒ (3)2 = 32 + h2 ⇒ h2 = 90 − 9 ⇒ h2 = 81 ⇒ h = 9
Logo, a altura do cone é 9 cm.
Por fim, calculamos o volume do cone:
V = (pi)"r2 ⋅ h ⇒ V = (pi)" ⋅ 32 ⋅ 9 ⇒ V = 27(pi)"
Portanto, o volume do cone é 27(pi)" cm3.
6. (UFV-MG) O trapézio retângulo a seguir sofre uma rotação de 360° em torno da base maior. Sabendo-se quê AB = 3 cm, CE = 5 cm e quê o volume do sólido obtído é 84(pi)" cm3, determine AC.

Resolução
O volume do cilindro gerado pela rotação do retângulo ABDC póde sêr determinado pela diferença entre o volume do sólido e o volume do cone gerado pela rotação do triângulo CDE. O triângulo CDE é retângulo em D.
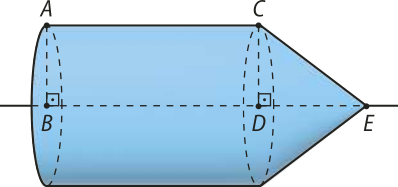
Indicando a medida de por h, aplicamos o teorema de Pitágoras no (triângulo)"CDE e obtemos:
52 = h2 + 32 ⇒ h2 = 16 ⇒ h = 4
Logo, a altura h do cone é 4 cm.
Calculando o volume do cone, temos:
Vcone = (pi)"r2 ⋅ h ⇒ Vcone = (pi)" ⋅ 32 ⋅ 4 = 12(pi)"
Calculando o volume do cilindro, temos:
Vcilindro = Vsólido − Vcone = 84(pi)" − 12(pi)" = 72(pi)"
Sendo a medida AC = x, temos:
Vcilindro = (pi)"r2 ⋅ x ⇒ 72(pi)" = (pi)" ⋅ 32 ⋅ x ⇒ x = 8
Portanto, AC = 8 cm.
Página cento e cinco
ATIVIDADES
19. ![]() Um funil de papel no formato de um cone reto tem 6 cm de diâmetro da base e 4 cm de altura. Qual é a área lateral dêêsse funil? (Use (pi)" = 3,14.)
Um funil de papel no formato de um cone reto tem 6 cm de diâmetro da base e 4 cm de altura. Qual é a área lateral dêêsse funil? (Use (pi)" = 3,14.)
Utilize a calculadora para auxiliá-lo nos cálculos.
47,1 cm2
20. Considere o triângulo retângulo ABC da figura.
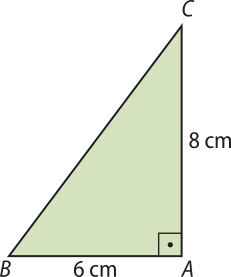
Determine a área total do sólido obtído pela rotação completa do triângulo em torno do lado:
a) ;
96(pi)" cm2
b) .
144(pi)" cm2
21. (hú- hê- érre jota) Uma linha poligonal fechada de três lados limita um triângulo de perímetro (éli)". Se ela gira em torno de um de seus lados, gera uma superfícíe de área S igual ao produto de (éli)" pelo comprimento da circunferência descrita pelo baricentro G da poligonal.
A figura a seguir mostra a linha (ABCA) quê dá uma volta em torno de BC.
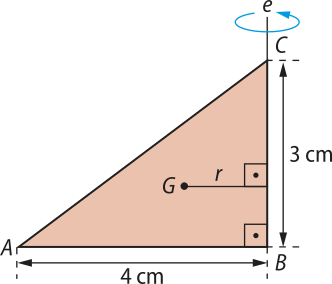
a) Esboce a figura gerada e indique o cálculo da área de sua superfícíe quê é igual a 36(pi)" cm2.
Ver as Orientações para o professor.
b) Calcule a distância r do baricentro G dessa linha ao eixo de rotação.
r = 1,5 cm
Saiba quê...
Baricentro é o ponto de encontro das medianas de um triângulo.
22. A geratriz de um cone equilátero méde 20 cm. Calcule a área da base (Sb)desse cone.
100(pi)" cm2
23. Determine a altura de um chapéu de cartolina de formato cônico construído a partir de um setor circular de raio 15 cm e ângulo central de 120°.
cm
24. A superfícíe lateral de um cone circular reto é feita com uma peça circular de papel de 20 cm de diâmetro da qual se retira um setor de radianos. Calcule a altura do cone quê tem essa superfícíe lateral.
cm
25. ![]() Uma cooperativa agrícola vai construir um silo para armazenamento de cereais em grãos. O silo terá o formato indicado na figura. O corpo será cilíndrico e a base terminará em um funil cônico.
Uma cooperativa agrícola vai construir um silo para armazenamento de cereais em grãos. O silo terá o formato indicado na figura. O corpo será cilíndrico e a base terminará em um funil cônico.
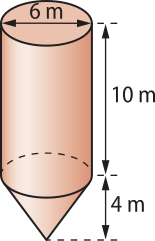
Para quê a superfícíe dêêsse silo não enferruje, será necessário pintá-lo externamente. Se, com uma lata de tinta, pode-se pintar 10 m2, qual é o número mínimo de latas para pintar a superfícíe total dêêsse silo? Use (pi)" = 3,14.
Utilize a calculadora para auxiliá-lo nos cálculos.
27 latas
26. É dada a superfícíe de um cone circular reto (sem fundo) de raio R e altura H. Cortando-o por uma de suas geratrizes e abrindo tal superfícíe, obtém-se um setor circular plano conforme a figura a seguir.
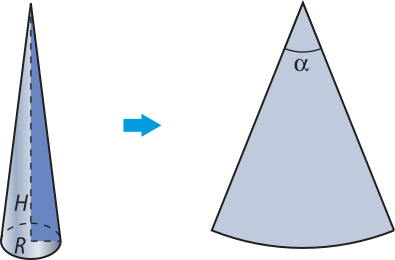
Qual é a relação entre R e H para quê o ângulo (alfa)" seja 45°?
Página cento e seis
27. (ITA-SP) As medidas, em metros, do raio da base, da altura e da geratriz de um cone circular reto formam, nesta ordem, uma progressão aritmética de razão 2 metros. Calcule a área total dêste cone em m2.
96(pi)" m2
28. Um cone circular reto tem 3 cm de raio da base e 15(pi)" cm2 de área lateral. Calcule seu volume.
12(pi)" cm3
29. Considere um triângulo retângulo isósceles cuja hipotenusa méde 2 cm. Determine o volume do sólido obtído pela rotação completa dêêsse triângulo em torno da hipotenusa.
cm3
30. O raio da base de um cone de revolução méde 3 cm, e o perímetro de sua secção meridiana méde 16 cm. Determine seu volume.
12(pi)" cm3
31. Na figura a seguir, tem-se um recipiente no formato de um cone circular reto, com um líquido quê atinge mêtáde de sua altura. Se V é a capacidade do cone, qual é o volume do líquido?
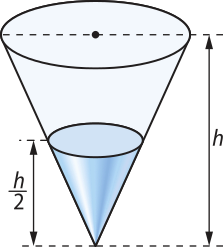
32. Pode-se considerar quê uma ampulheta é formada por dois cones rétos idênticos, unidos pelo vértice, inscritos em um cilindro reto. Determine a razão entre o volume de um dos cones e o volume do cilindro.
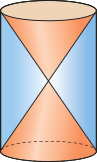
33. A medida dos lados de um triângulo equilátero ABC é 5 dm. O triângulo gira em torno de uma reta r do plano do triângulo, paralela ao lado BC e passando pelo vértice A. Calcule o volume do sólido gerado pela rotação dêêsse triângulo.
dm3
34. Cisternas são depósitos quê captam e armazenam á gua da chuva. São muito utilizadas em regiões em quê há escassez de á gua e passaram a sêr adotadas também em grandes centros urbanos, por causa do racionamento gerado pêlos baixos níveis de á gua das represas. Um modelo de reservatório muito utilizado é formado por um cilindro sobreposto por um cone de mesma base, como é possível vêr na figura.

Uma escola pretende construir uma cistérna cujo reservatório terá o mesmo formato do modelo da imagem. Entre as especificações do projeto, a escola decidiu quê a cistérna deve ter altura mássima de 4 metros e capacidade para armazenar no mínimo 12 mil litros e no mássimo 24 mil litros de á gua.
Elabore um problema envolvendo a construção de uma cistérna quê atenda às necessidades e condições dessa escola.
Resposta pessoal.
35. Imagine quê, para arrecadar dinheiro para a execução de uma ação social na sua comunidade, fosse proposta a venda de canudinhos de doce de leite com formato cônico. Para isso, seria necessária a compra dos canudinhos (cones vazios) e de doce de leite para o recheio. Sobre essa situação, responda:
a) Para calcular a capacidade de cada canudinho, sêria necessário medir quais dimensões dos cones vazios? Como isso poderia ser feito?
b) Se o doce de leite foi adquirido em pótes cilíndricos cuja altura é igual à altura dos canudinhos e o raio da base é o quádruplo do raio interno da base dos canudinhos, quantos canudinhos de doce de leite é possível montar com um póte de doce de leite?
c) Se o raio da base interna dos canudinhos for igual a 1 cm e sua altura for igual a 6 cm, qual será a massa, em grama, de doce de leite usada em cada canudinho, sabendo quê a densidade do recheio é 1,32 g/mL? Use (pi)" = 3,14.
d) Você consegue propor uma ação social quê seria benéfica para a sua comunidade? Compartilhe-a com os côlégas e o professor.
Ver as Orientações para o professor.
Página cento e sete
FÓRUM
Captação de á gua da chuva
A crise hídrica é uma realidade cada vez mais presente em diversas regiões do mundo, o quê exige a implementação de medidas criativas e sustentáveis para garantir o acesso contínuo das populações à á gua potável. Nesse contexto, a captação de á gua da chuva surge como uma solução promissora e eficaz.
A á gua da chuva, muitas vezes subestimada e desperdiçada, póde sêr uma fonte valiosa de recursos hídricos. Por meio de sistemas de captação adequados, é possível coletar, armazenar e utilizar essa á gua para diferentes finalidades, desde a irrigação de jardins até a descarga de vasos sanitários.
Um dos principais benefícios da captação de á gua da chuva é a redução da pressão sobre os recursos hídricos tradicionais, como rios e aqüíferos. Ao aproveitar a á gua pluvial, diminuímos a dependência de outras fontes hídricas e contribuímos para a conservação dos éco-sistemas aquáticos. Além díssu, ao incorporar práticas de reaproveitamento da á gua em nossas rotinas, estamos adotando uma abordagem responsável em relação ao uso dos recursos naturais.
É importante ressaltar quê, dependendo do uso quê se fará da á gua captada, são necessários investimento e tratamento adequados. No entanto, para atividades como regar um jardim ou lavar um quintal, por exemplo, pode-se coletar a á gua de maneira simples, sem a necessidade de equipamentos sofisticados ou grandes investimentos.
![]() • Junte-se a seus côlégas e comentem se vocês já observaram a prática da reutilização de á gua da chuva em lugares quê frequentam, como suas casas, a escola ou outros ambientes. Discutam em quê atividades rotineiras, além das citadas no texto, a á gua captada da chuva poderia sêr empregada.
• Junte-se a seus côlégas e comentem se vocês já observaram a prática da reutilização de á gua da chuva em lugares quê frequentam, como suas casas, a escola ou outros ambientes. Discutam em quê atividades rotineiras, além das citadas no texto, a á gua captada da chuva poderia sêr empregada.

Ver as Orientações para o professor.
Página cento e oito
esféra
Muitos objetos e construções do nosso cotidiano têm formatos quê lembram esferas ou partes de uma esféra. Uma bola de futeból é um exemplo de objeto com formato muito próximo ao de uma esféra, ainda quê não seja rigorosamente uma esféra. O próprio planêta Terra, como sabemos, é muito parecido com uma esféra quando observado à distância, mas, por vários motivos, como o fato de sêr achatado nos polos, não possui o formato exato de uma esféra.
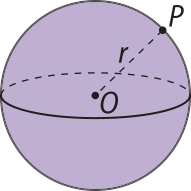
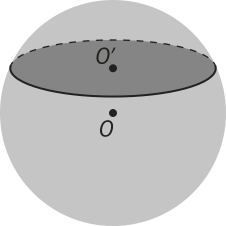
Vamos considerar um ponto O e um número real r positivo, como indicado na figura.
O conjunto de todos os pontos P do espaço cuja distância ao ponto O é igual a r é denominado superfícíe esférica de centro O e raio r.
O sólido limitado por uma superfícíe esférica chama-se esféra. Dessa maneira, a esféra de centro O e raio r é o conjunto dos pontos do espaço cuja distância ao ponto O é menor ou igual a r.
De modo bastante simples, podemos dizêr quê a superfícíe esférica é a"casca", enquanto a esféra é a reunião da"casca" com o"miolo".
As denominações centro e raio são aplicadas indiferentemente a uma superfícíe esférica ou à esféra por ela limitada.
Saiba quê...
Por definição, geoide é o nome dado ao modelo quê representa o formato real do planêta Terra.

Página cento e nove
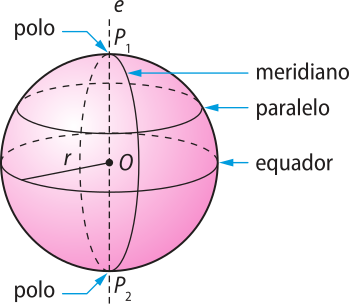
Dada uma esféra, definimos eixo como qualquer reta quê contém o centro da esféra e o indicamos por e.
Agora, fixado um eixo e, definimos os seguintes elemêntos:
• Polos: são os pontos de intersecção da superfícíe esférica com o eixo e; são indicados por P1 e P2;
• Equador: é a circunferência ôbitída como intersecção entre a superfícíe esférica e um plano perpendicular ao eixo e quê passa pelo centro da esféra;
• Paralelos: são as circunferências obtidas como intersecções entre a superfícíe esférica e planos perpendiculares ao eixo e. São, portanto, coincidentes com o equador ou paralelos a ele;
• Meridianos: circunferências obtidas como intersecções da superfícíe esférica com planos quê contêm o eixo e.
Os círculos obtidos pela intersecção da esféra com um plano quê passa pelo centro O são chamados círculos mássimos.
Cada círculo mássimo divide a esféra em duas partes iguais chamadas de hemisférios.
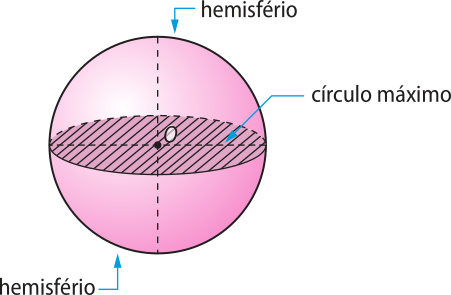
Saiba quê...
Os mesmos elemêntos da esféra foram adotados para dividir o planêta Terra. Ele é dividido em dois hemisférios (Norte e Sul), a partir da linha do equador, quê corresponde a uma circunferência mássima do planêta, medindo 40.075 km.
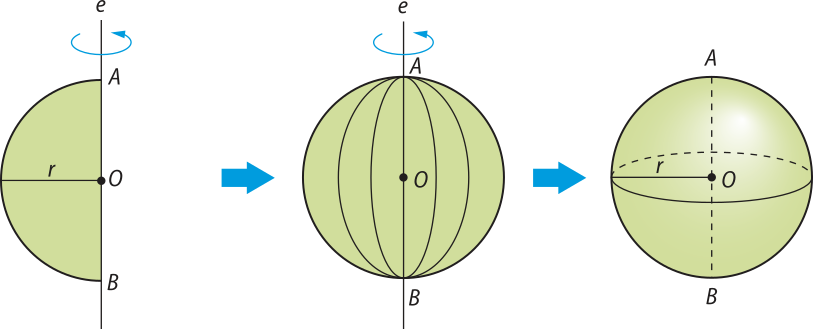
A esféra também póde sêr ôbitída pela rotação completa de um semicírculo em torno de um eixo quê contém seu diâmetro. Por isso, o eixo e também é chamado de eixo de rotação.
Página cento e dez
Secção de uma esféra
Considere um plano (alfa)" cuja distância ao centro O de uma esféra seja menor do quê o raio r. A intersecção entre esse plano e a esféra é um círculo, como representado na figura a seguir.
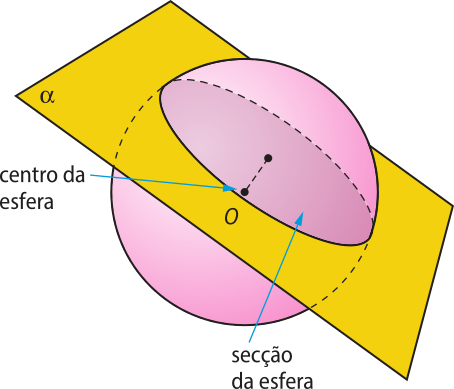
Quando o plano passa pelo ponto O (centro da esfera), como já estudamos, o círculo obtído é chamado de círculo mássimo.
Volume de uma esféra
Rolamentos são peças utilizadas em máquinas para reduzir o atrito entre partes móveis. O tipo de rolamento mais utilizado é o de esferas, quê apresenta, em seu interior, pequenas esferas de aço, como mostra a imagem. Para saber quanto aço foi utilizado nessas esferas, é necessário determinar o volume dessa forma geométrica. Mas como fazemos isso?

Para calcular o volume de uma esféra de raio r, vamos utilizar o princípio de Cavalieri. Considere um cilindro equilátero de altura 2r e raio da base r. Retirando dois cones circulares rétos, de altura r e raio da base r, cujas bases coincidem com as bases dêêsse cilindro, obtemos o sólido A (conhecido como anticlepsidra), representado na figura a seguir na côr laranja.
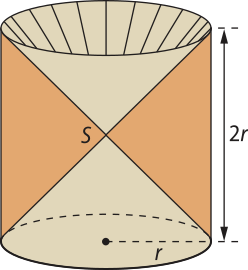
O volume do sólido A é igual à diferença entre o volume do cilindro equilátero e os volumes dos dois cones circulares rétos, ou seja:
VA = Vcilindro − 2Vcone = (pi)"r2 ⋅ 2r − 2 ⋅ (pi)"r2 ⋅ r = 2(pi)"r3 − (pi)"r3 = (pi)"r3
Página cento e onze
Agora, vamos considerar uma esféra E de raio r e o sólido A, apoiados em um mesmo plano (alfa)", conforme mostra a figura a seguir.
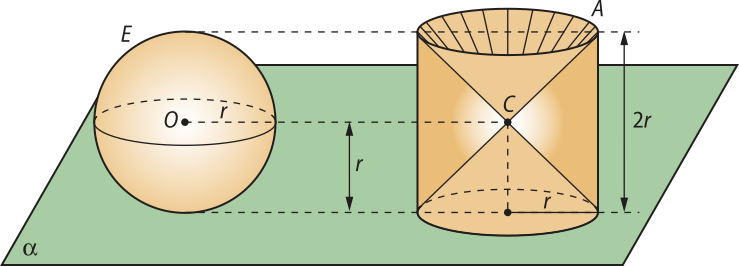
Considere também um plano (beta)" paralelo a (alfa)" e secante aos sólidos quê secciona a esféra E e o sólido A a uma distância d do centro da esféra O, como mostra a figura a seguir.
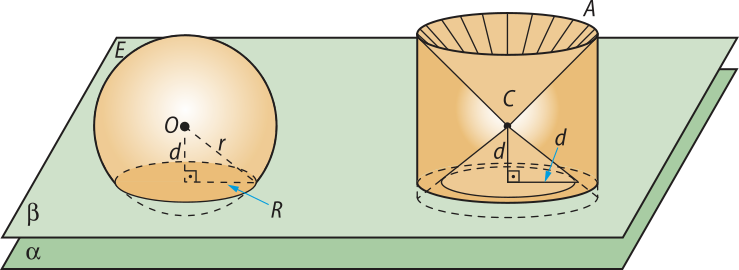
O plano (beta)" determina um círculo na esféra E, cujo raio indicaremos por R. Pelo teorema de Pitágoras, temos:
r2 = R2 + d2 ⇒ R2 = r2 − d2
Assim, a área S1 do círculo é dada por:
S1 = (pi)"R2 = (pi)"(r2 − d2) I
A secção determinada pelo plano (beta)" no sólido A é uma coroa circular de raios r e d, e sua área S2 é dada por:
S2 = (pi)"(r2 − d2) II
Assim, comparando I e II, verificamos quê a área da secção plana da esféra E (círculo) é igual à área da secção plana do sólido A (coroa circular).
Logo, pelo princípio de Cavalieri, a esféra E tem o mesmo volume quê o sólido A, portanto o volume V da esféra é dado por:
V = (pi)"r3
Para acessar
• O quê é o"problema dos beijos" quê atormenta os matemáticos há séculos. BBC nius Brasil, [s. l.], 18 jun. 2023. Disponível em: https://livro.pw/xwcpy. Acesso em: 10 out. 2024.
Você sabe qual é a maneira mais eficiente de empilhar objetos esféricos? Leia a matéria e descubra as dificuldades envolvidas nesse problema.
Página cento e doze
Área de uma superfícíe esférica
Agora quê já aprendemos como determinar o volume de uma esféra, vamos usar esse resultado para verificar o cálculo da área de uma superfícíe esférica.
Uma esféra póde sêr imaginada como a reunião de vários sólidos parecidos com"pirâmides" de vértices em C (centro da esfera), como representado na figura a seguir.
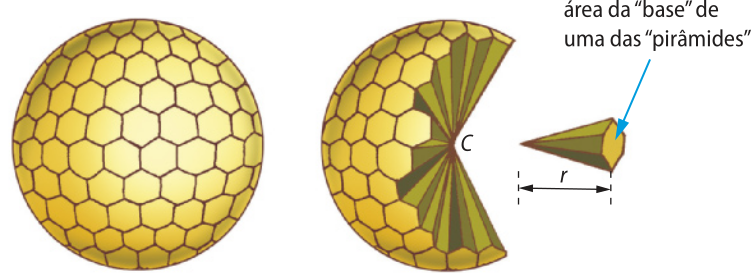
Esses sólidos não são verdadeiramente pirâmides, pois a"base" de cada sólido é uma superfícíe arredôndá-da. No entanto, quanto mais sólidos considerarmos, mais a base deixa de sêr arredôndá-da e se torna mais plana, aproximando-se, assim, da forma de uma pirâmide.
A altura de cada"pirâmide" é o raio r da esféra.
Considere uma esféra de centro C decomposta em uma quantidade de n sólidos parecidos com pirâmides cujos vértices se encontram no centro da esféra.
Desse modo, a superfícíe esférica fica dividida em n"polígonos", bases das “pirâmides”, cujas áreas chamaremos de S1, S2, S3, ..., Sn. Para n muito grande, cada "polígono" tem área e perímetro muito pequenos, e a soma das áreas de todos esses “polígonos” se aproxima da área da superfícíe esférica S:
S1 + S2 + S3 + ... + Sn ≃ S I
Além díssu, quanto maior for o número n, mais a soma dos volumes de todas essas"pirâmides" se aproxima do volume da esféra. O volume de uma pirâmide é dado por Vpirâmide = Sb ⋅ h e, sêndo h = r (raio da esfera) e Sb = Si,, quê é a área do i-ésimo polígono, podemos escrever o volume da i-ésima pirâmide como Vi = Si ⋅ r, i = 1, 2,..., n.
Assim, se V é o volume da esféra, para n muito grande, temos:
V ≃ V1 + V2 + V3 + ... + Vn
V ≃ ⋅ r(S1+ S2 + S3 +... + Sn) II
Substituindo I em II, obtemos V ≃ S ⋅ r
Logo, como V = , temos: S ⋅ r ⇒ S ≃ 4(pi)"r2
Estudamos quê quanto maior for o número n, mais S se aproxima de 4(pi)"r2. Logo, fazendo n tender ao infinito, obtemos a área da superfícíe esférica:
S = 4(pi)"r2
Página cento e treze
Cunha esférica
Chamamos de cunha esférica o sólido gerado pela rotação, por um ângulo de medida (alfa)" (0° < (alfa)" ≤ 360°), de um semicírculo de raio r em torno do eixo quê contém seu diâmetro, como mostrado a seguir.
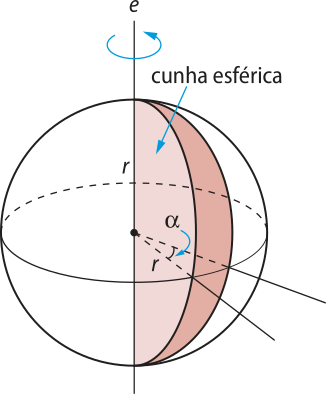
O volume da cunha esférica póde sêr calculado por meio de uma regra de três quê compara esse sólido com a esféra.

(alfa)" ⋅ (pi)"r3 = 360° ⋅ Vcunha ⇒ Vcunha =
Logo:
Vcunha =
Fuso esférico
Chamamos de fuso esférico a superfícíe gerada pela rotação, por um ângulo de medida (alfa)" (0° < (alfa)" ≤ 360°), de uma semicircunferência de raio r em torno do eixo quê contém seu diâmetro, como mostrado na figura a seguir.
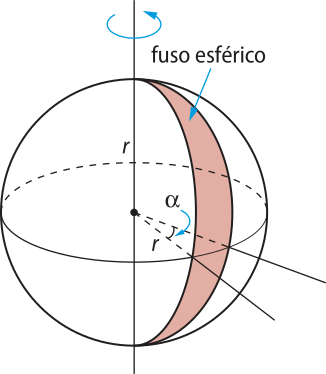
A área do fuso esférico póde sêr calculada por meio de uma regra de três quê o compara à superfícíe esférica.
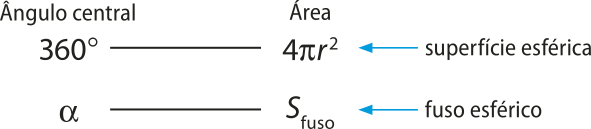
(alfa)" ⋅ 4(pi)"r2 = 360° ⋅ Sfuso ⇒ Sfuso =
Logo:
Sfuso =
Pense e responda
Como seriam as fórmulas do volume da cunha esférica e da área do fuso esférico se o ângulo (alfa)" fosse considerado em radiano?
Vcunha = (alfa)"r3; Sfuso = 2(alfa)"r2
Página cento e quatorze
ATIVIDADES RESOLVIDAS
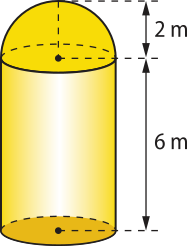
7. Um silo tem o formato de um cilindro circular reto (com fundo) sôbi uma semi-esféra, como na figura. Determine o volume dêêsse silo, sabendo quê o raio do cilindro méde 2 m e quê a altura do silo méde 8 m.

Resolução
O volume do silo é igual à soma dos volumes de uma semi-esféra de raio 2 m e de um cilindro de raio 2 m e altura 6 m.
Vsemi-esféra =
Vcilindro = (pi)" ⋅ 22 ⋅ 6 = 24(pi)"
Vsilo = + 24(pi)" = (pi)"
Portanto, o volume do silo é m3.
8. Para medir o diâmetro de uma esféra maciça, João utilizou a seguinte estratégia: colocou certa quantidade de á gua em um recipiente de formato cilíndrico de raio 10 cm e altura 20 cm. Em seguida, mergulhou a esféra na á gua, de modo quê ela ficou totalmente submersa. Ele, então, verificou quê a altura da á gua no recipiente subiu 2 cm. Assim, pôdi determinar o diâmetro da esféra. Qual é esse diâmetro?
Resolução
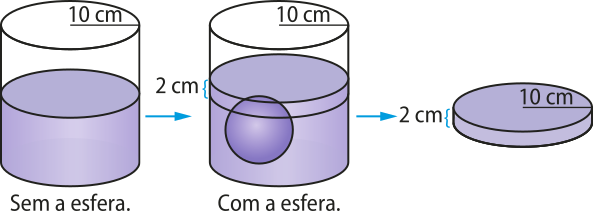
O volume da esféra é equivalente ao volume de á gua deslocado, o qual, por sua vez, corresponde ao volume de um cilindro de raio 10 cm e altura 2 cm.
Vdeslocado = (pi)"r2 ⋅ h = (pi)" ⋅ 102 ⋅ 2 = 200(pi)"
Vesféra = (pi)"R3 = 200(pi)" ⇒ R = ≃ 5,3
Como o diâmetro da esféra é o dôbro do seu raio, ele é aproximadamente igual a 10,6 cm.
9. A professora Cristina produziu com os estudantes de sua turma da pré-escola enfeites de Natal no formato de esferas, com 12 cm de diâmetro cada uma. Para pintar a superfícíe dessas esferas, ela dispõe de uma latinha de tinta, com a qual, conforme informação do fabricante, é possível pintar até 5 m2 de superfícíe.
Nessas condições, qual é o número mássimo de enfeites quê a turma de Cristina poderá pintar?
Resolução
Em cada esféra, temos: r = ⇒ r = 6
Sesféra = 4(pi)"r2 = 4 ⋅ (pi)" ⋅ 62
Sesféra = 144(pi)"
Considerando (pi)" = 3,14, a área da superfícíe esférica é 452,16 cm2.
Como é possível pintar até 5 m2 (50.000 cm2) com a latinha de tinta, temos: ≃ 110,58
Portanto, a turma da professora Cristina poderá pintar até 110 enfeites.
10. Considere uma esféra cuja superfícíe tenha área igual a 676(pi)" cm2. Nessas condições, determine:
a) a medida do raio da esféra;
b) o volume da esféra.
Resolução
a) Cálculo do raio da esféra:
S = 676(pi)" ⇒ 4(pi)"r2 = 676(pi)" ⇒ r2 = 169
Como r é positivo, temos r = 13.
Portanto, o raio da esféra é 13 cm.
b) Cálculo do volume:
V = (pi)"r3 ⇒ V = (pi)" ⋅ 133 ⇒ V = (pi)"
Portanto, o volume da esféra é (pi)" cm3.
Página cento e quinze
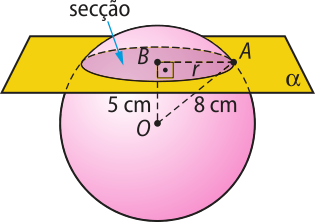
11. Uma esféra de raio 8 cm é seccionada por um plano distante 5 cm de seu centro. Calcule o raio do círculo determinado pela secção.
Resolução
A intersecção do plano (alfa)" com a esféra determina a secção indicada na figura.
Do triângulo retângulo OBA, tem-se:
82 = 52 + r2 ⇒ 64 = 25 + r2 ⇒ r2 = 39
Como r é positivo, r = .
Portanto, o raio do círculo determinado pela secção é cm.
ATIVIDADES
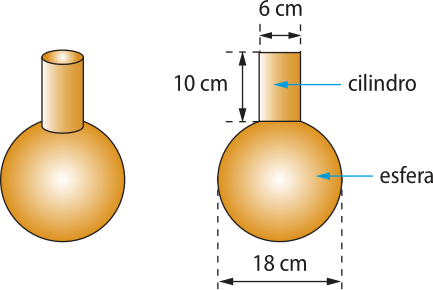
36. ![]() Calcule, em mililitro, a capacidade aproximada do recipiente indicado na figura. Adote (pi)" = 3,14. Utilize a calculadora para auxiliá-lo nos cálculos.
Calcule, em mililitro, a capacidade aproximada do recipiente indicado na figura. Adote (pi)" = 3,14. Utilize a calculadora para auxiliá-lo nos cálculos.
3.334,68 mL
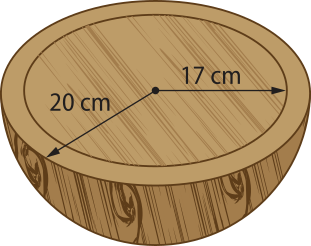
37. O recipiente da imagem é feito de madeira e tem densidade 0,7 g/cm3. Tanto sua parte externa quanto a interna correspondem a superfícies de semiesferas, e seus raios estão indicados na imagem. Calcule a massa do recipiente em kilograma.
aproximadamente 4,52 kg
38. Um reservatório no formato de uma semi-esféra tem 18 m de diâmetro. Qual é o volume de á gua quê cabe nesse reservatório?
486(pi)" m3
39. (Unifesp) Um recipiente, contendo á gua, tem a forma de um cilindro circular reto de altura h = 50 cm e raio r = 15 cm.
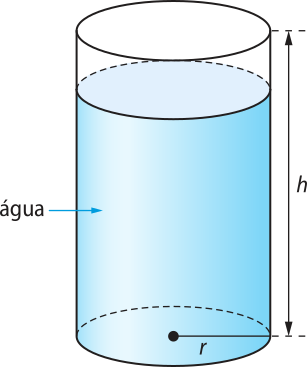
êste recipiente contém 1 litro de á gua a menos quê sua capacidade total.
a) Calcule o volume de á gua contido no cilindro (use (pi)" = 3,14).
34,325 L
b) Qual deve sêr o raio R de uma esféra de ferro quê, introduzida no cilindro e totalmente submersa, faça transbordarem exatamente 2 litros de á gua?
aproximadamente 8,95 cm
40. (PUC-RJ) B1 é uma bola esférica de volume V1. B2 é uma bola esférica de volume V2, cujo raio é o triplo do raio de B1.
Escolha a alternativa correta.
a) V2 = 3V1
b) V2 = 9V1
c) V2 = 12V1
d) V2 = 27V1
e) V2 = 81V1
alternativa d
Página cento e dezesseis
41. (Eear-SP) Um objeto metálico maciço é formado por um cilindro circular reto, de raio da base medindo R cm e H cm de altura, justaposto a 2 semiesferas de raio R cm, conforme a figura dada.
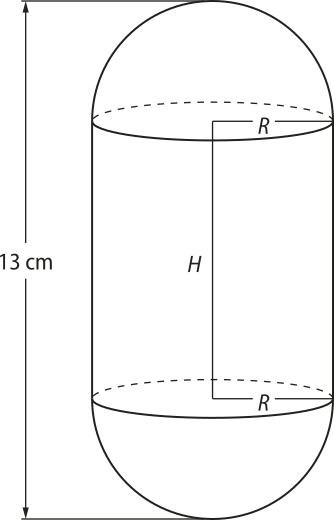
Se o objeto tem 13 cm de comprimento e 78(pi)" cm2 de área total, então o valor de H é _____ cm.
a) 4
b) 5
c) 6
d) 7
alternativa d
42. Uma esféra está inscrita em um cilindro equilátero de raio da base a. Qual é a razão entre o volume V1 da esféra e o volume V2 do cilindro?
43. Uma casquinha de sorvete com formato de cone tem 3 cm de diâmetro da base e 6 cm de profundidade. Depois de totalmente preenchida, ainda é adicionada à casquinha meia bola de sorvete, conforme a imagem. Já o recipiente cilíndrico quê armazena o sorvete tem 18 cm de diâmetro e 5 cm de altura.

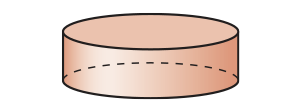
Determine o número de casquinhas quê podem sêr servidas com o sorvete armazenado em um recipiente cheio.
60 casquinhas
44. (PUC-RS) A região R da figura está limitada por três semicírculos.
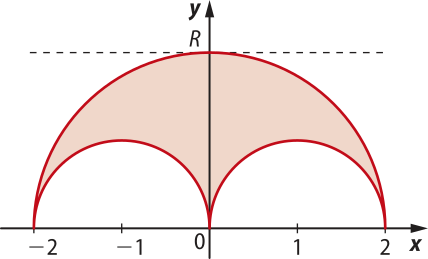
Sabendo quê R efêtúa uma volta completa em torno do eixo x, calcule o volume do sólido gerado.
8(pi)"
45. Em uma festa de arrecadação de fundos em uma escola, os pais de uma estudante resolveram fazer brigadeiros para vender durante a festa. Solicitando ajuda à filha, pediram a ela quê confeccionasse caixinhas de papel-cartão para colocar cada um dos brigadeiros. As caixinhas confeksionadas deveriam ter formato cúbico. Antes de sêr armazenado na caixinha, o brigadeiro é colocado em uma forminha de formato cilíndrico, de modo quê mêtáde do doce, de formato esférico, fique para fora da forminha.

![]()
![]() Forme um pequeno grupo com seus côlégas e, juntos, respondam às kestões a seguir.
Forme um pequeno grupo com seus côlégas e, juntos, respondam às kestões a seguir.
Para todas as situações necessárias, considerem (pi)" = 3,14.
Utilizem a calculadora para auxiliá-los nos cálculos.
a) Qual é o volume aproximado de cada brigadeiro?
33,49 cm3
b) Qual é a capacidade aproximada das forminhas de formato cilíndrico?
25,12 cm3
c) Sabendo quê cada fô-lha de papel-cartão tem 68 cm × 48 cm e quê não há sobreposição de material na montagem, quantas caixinhas de aresta igual a 4 cm poderão sêr confeksionadas?
34 caixinhas
Página cento e dezessete
46. Sabendo quê a área de uma superfícíe esférica é 8(pi)" cm2, calcule o raio da esféra.
cm
47. Um plano (alfa)" secciona uma esféra de raio 20 cm. A distância do centro da esféra ao plano (alfa)" é 12 cm. Calcule a área da secção ôbitída.
256(pi)" cm2
48. Qual é a área total da superfícíe esférica gerada pela rotação completa do semicírculo da figura em torno de seu diâmetro ?
100(pi)" cm2
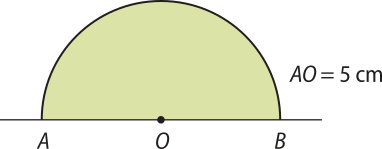
49. ![]() Supondo quê a Terra seja uma esféra perfeita e sabendo quê seu raio é de aproximadamente 6.400 km, determine:
Supondo quê a Terra seja uma esféra perfeita e sabendo quê seu raio é de aproximadamente 6.400 km, determine:
a) a área total da superfícíe terrestre (use (pi)" = 3);
491.520.000 km2
b) o valor percentual quê ocupa o continente americano, cuja área é de 42.215.000 km2, em relação à superfícíe total da Terra.
Utilize a calculadora para auxiliá-lo nos cálculos.
aproximadamente 8,59%
50. (Faap-SP) A área da superfícíe de uma esféra e a área total de um cone reto são iguais. Determine o raio da esféra, sabendo quê o volume do cone é 12(pi)" dm3 e o raio da base é 3 dm.
dm
51. (CPAEAM) Uma esféra com centro em O possui volume igual a cm3. Se tomarmos um plano e o fizermos interceptar essa esféra a uma distância d do seu centro, a seção plana circular resultante, de centro O’, terá área igual a 24(pi)" cm2 (figura abaixo). Assim, de acôr-do com os dados, calcule o valor d, ou seja , e assinale a opção correta.
a) 1 cm
b) 3 cm
c) 5 cm
d) 7 cm
e) 10 cm
alternativa c
52. Uma esféra é seccionada por um plano (alfa)" distante 12 cm do centro da esféra. O raio da secção ôbitída é 9 cm. Calcule o volume da esféra.
4.500(pi)" cm3
53. (UPF-RS) Com inspiração na arquitetura, na cultura e nas cores da bandeira do Catar, a bola oficial da cópa do Mundo de 2022 foi denominada Al Rihla, quê significa “a jornada” em árabe (Fonte: https://livro.pw/pfugv).
A bola é revestida de péle de poliuretano com uma nova forma de painel de 20 peças, quê melhora sua aerodinâmica. A figura a seguir apresenta a bola e o seu painel de peças.

A Al Rihla tem circunferência de cerca de 70 cm. Considere quê, para a produção de uma peça da bola, a quantidade de péle de poliuretano foi aumentada em 10%, devido aos rekórtis quê devem sêr feitos. A quantidade dêêsse material quê será necessária para a produção de uma bola, em cm2, é:
a)
b)
c)
d) 4,4 × 352
e)
alternativa b
54. Calcule a área de um fuso esférico de raio 2 m e ângulo 135°.
6(pi)" m2
55. Calcule o volume de uma cunha esférica de raio 6 cm e ângulo 45°.
36(pi)" cm3
Página cento e dezoito
Projeções cartográficas
Uma parte de nosso estudo com cilindros e cones envolveu o cálculo da área de suas superfícies. Para isso, observamos a planificação dêêsses sólidos geométricos. No entanto, essa não foi a maneira utilizada para obtêr a superfícíe da esféra, o quê nos traz uma dúvida: é possível planificar uma esféra?
A resposta é não, não é possível planificar uma esféra. Então como podemos representar sua superfícíe no plano?
Junto a essa quêstão, devemos responder também a outra pergunta: para que representar uma superfícíe esférica no plano?
A resposta para essas perguntas aparece quando vemos um planisfério.
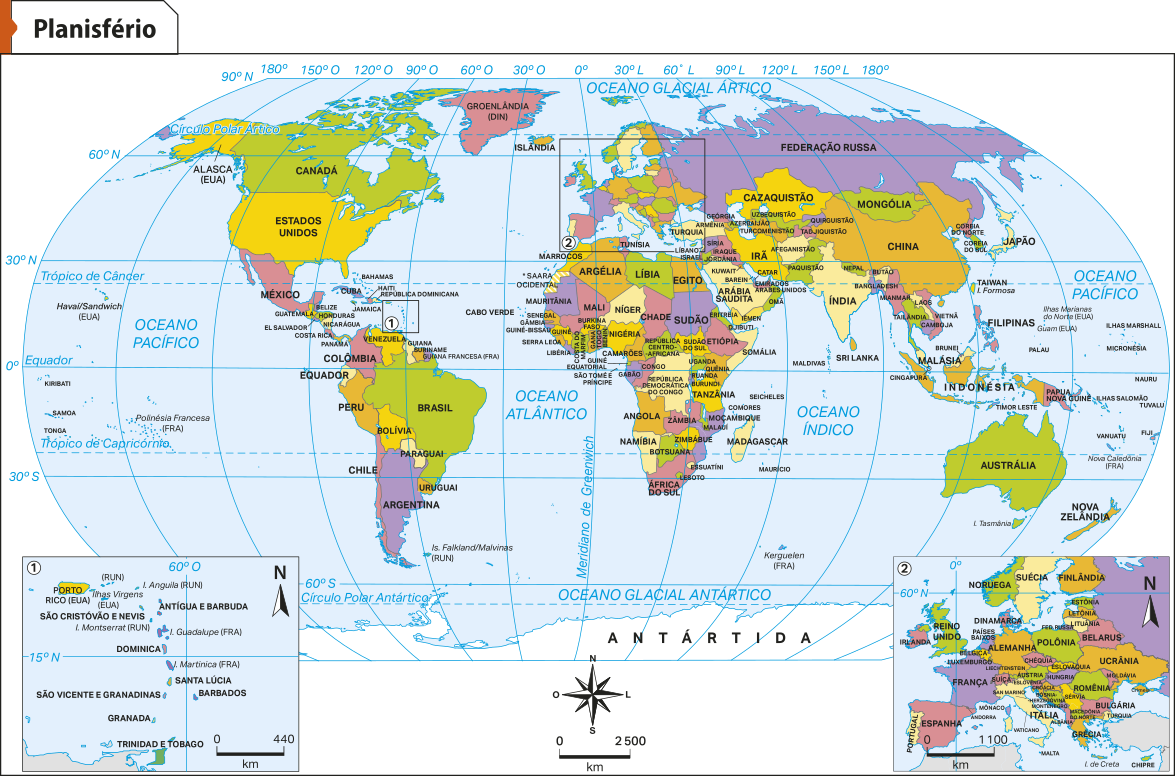
Fonte: INSTITUTO BRASILEIRO DE GEOGRAFIA E ESTATÍSTICA. Atlas geográfico escolar. 9. ed. Rio de Janeiro: hí bê gê hé, 2023. p. 41a.
Mapas são representações planas de um corpo aproximadamente esférico, a Terra. Eles são importantes pois permitem a visualização de diversos dêtálhes quê seriam impossíveis em globos, já quê, para isso, estes precisariam sêr muito grandes, o quê os tornaria difíceis de manusear e de transportar.

Saiba quê...
Planisférios são mapas quê mostram todo o planêta de uma só vez. Também são chamados de mapas-múndi.
Página cento e dezenove
Como não existe uma representação plana perfeita da esféra (uma planificação), é de se imaginar quê as representações quê existam apresentem algum tipo de distorção. Por isso, procuraram-se maneiras de desenhar um mapa quê, de alguma forma, apresentasse poucas distorções, seja nos comprimentos, seja nas áreas ou nos formatos dos continentes. Essas"maneiras" são as projeções cartográficas.
Cada projeção cartográfica objetiva manter fiel algum aspecto, quê póde sêr a dimensão, a forma etc., em detrimento de outro. Por isso, cada projeção cartográfica responde a determinado objetivo de quem a apresenta, seja político, seja econômico ou cartográfico.
Cada tipo de projeção é conhecido pela superfícíe em quê o glôbo terrestre é projetado. Neste Capítulo estudaremos a projeção cilíndrica, a cônica e a plana, isto é, aquelas em quê o glôbo terrestre é projetado, respectivamente, sobre um cilindro, um cone e um plano.
Para acessar
• O QUE é a projeção Gall-Peters, mapa quê promete acabar com"4 séculos de visão colonialista" do mundo. BBC nius Brasil, [s. l.], 23 mar. 2017. Disponível em: https://livro.pw/qskho. Acesso em: 10 out. 2024.
Reportagem da BBC nius Brasil sobre os aspectos políticos envolvidos nas projeções cartográficas.
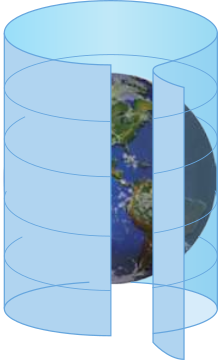
Projeção cilíndrica
É a projeção dos paralelos e meridianos sobre um cilindro quê envolve a Terra e quê, posteriormente, é planificado.
Saiba quê...
Na bibliografia cartográfica, já foram descritos 400 tipos distintos de projeção.

FERREIRA, Graça Maria L. Atlas geográfico: espaço mundial. Visualização cartográfica: Marcello Martinelli. 5. ed. rev. e atual. São Paulo: Moderna, 2019. p. 10.

Página cento e vinte
Projeção cônica
É a projeção do glôbo terrestre sobre um cone, quê é planificado em seguida. Sua utilização se dá quando quêremos representar as latitudes médias. Nessa projeção, as distorções aumentam conforme a representação se afasta do paralelo de contato com o cone, de modo que essa projeção é utilizada quando queremos produzir mapas regionais.
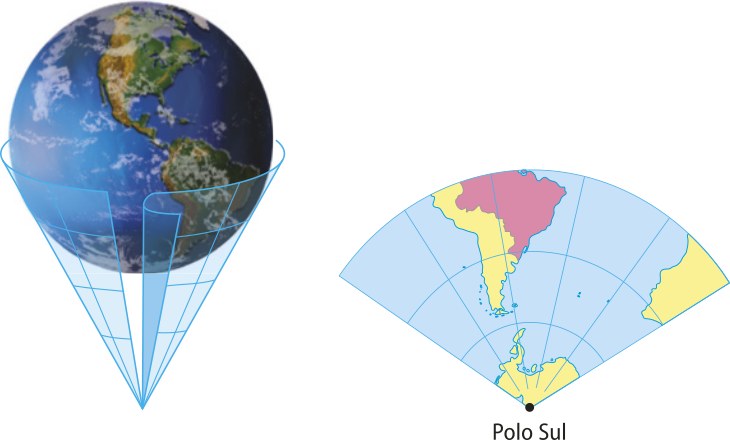
Fonte: FERREIRA, Graça Maria L. Atlas geográfico: espaço mundial. Visualização cartográfica: Marcello Martinelli. 5. ed. rev. e atual. São Paulo: Moderna, 2019. p. 10.
Projeção plana
Também conhecida como projeção azimutal, é aquela feita sobre um plano a partir de um determinado ponto, ou seja, de um ponto de vista. Esse tipo de projeção deforma áreas distantes dêêsse ponto de vista central. É bastante utilizada para a representação das áreas polares.
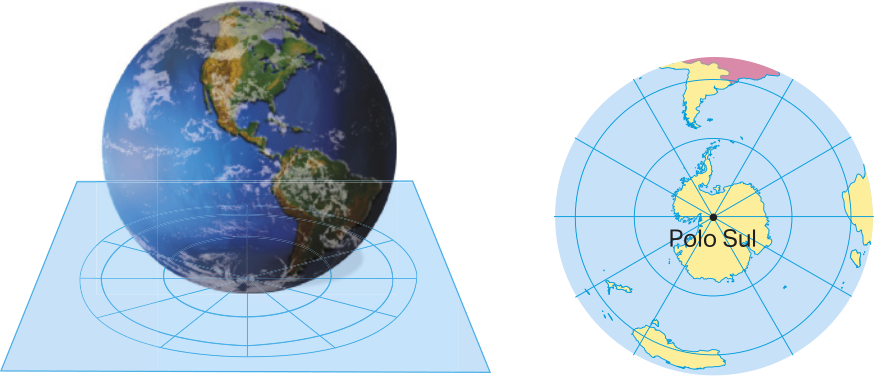
Fonte: FERREIRA, Graça Maria L. Atlas geográfico: espaço mundial. Visualização cartográfica: Marcello Martinelli. 5. ed. rev. e atual. São Paulo: Moderna, 2019. p. 10.
As projeções cartográficas têm duas classificações principais: quanto à superfícíe de projeção e quanto às propriedades. As projeções estudadas anteriormente são classificadas de acôr-do com a superfícíe de projeção.
Quanto às propriedades, temos as seguintes classificações:
• Equivalente: preserva áreas.
• Conforme: preserva ângulos.
• Equidistante: preserva comprimentos.
Página cento e vinte e um
Observe os exemplos a seguir, quê mostram o planisfério representado por três das projeções cartográficas mais conhecidas atualmente: a projeção de píters, a de Robinson e a de Mercator.
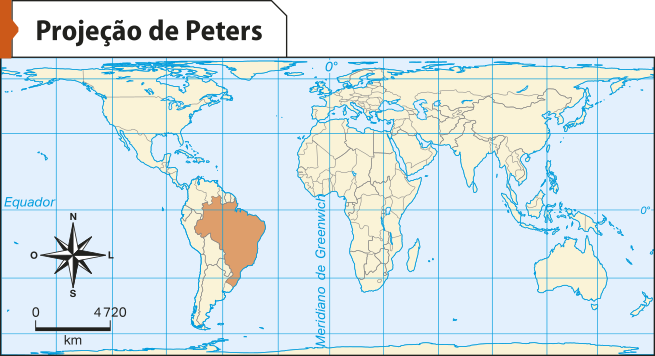
Fonte: INSTITUTO BRASILEIRO DE GEOGRAFIA E ESTATÍSTICA. Atlas geográfico escolar. 9. ed. Rio de Janeiro: hí bê gê hé, 2023. p. 26.
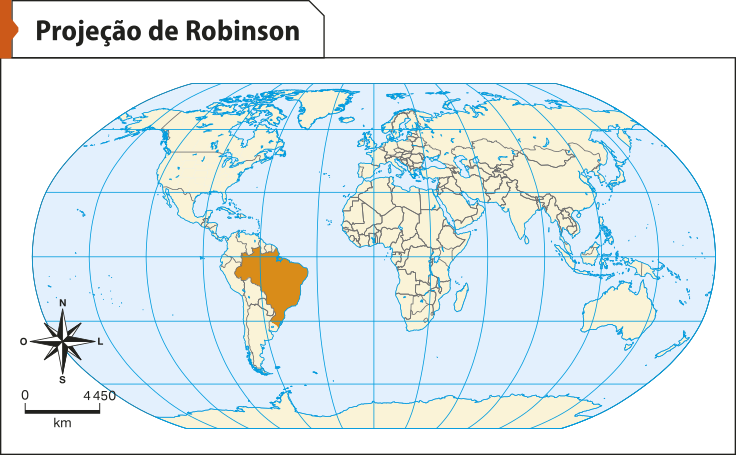
Fonte: INSTITUTO BRASILEIRO DE GEOGRAFIA E ESTATÍSTICA. Atlas geográfico escolar. 9. ed. Rio de Janeiro: hí bê gê hé, 2023. p. 29.
Acompanhe algumas diferenças entre essas projeções.
• A projeção de píters é uma projeção cilíndrica e equivalente, quê distorce o formato dos continentes, porém se aproxima mais das áreas deles.
• A projeção de Robinson é uma projeção afilática (que não é conforme, nem equivalente, nem equidistante) e pseudocilíndrica (não possui nenhuma superfícíe de projeção, porém se assemelha à projeção cilíndrica).
• A projeção de Mercator é uma projeção conforme e cilíndrica, bastante utilizada para representar o mundo. As distorções ocorrem sobretudo nos polos.
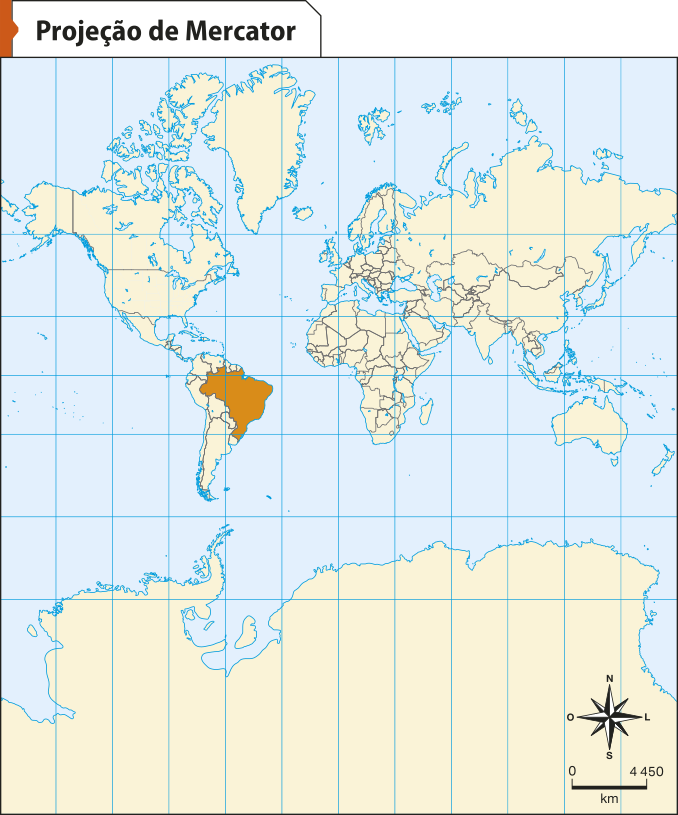
Fonte: INSTITUTO BRASILEIRO DE GEOGRAFIA E ESTATÍSTICA. Atlas geográfico escolar. 9. ed. Rio de Janeiro: hí bê gê hé, 2023. p. 28.
Página cento e vinte e dois
ATIVIDADE RESOLVIDA
12. Leia a tirinha a seguir.

QUINO, J. L. Toda Mafalda. São Paulo: Martins Fontes, 2010. p. 348. Tira 2.
Na tirinha, a personagem Liberdade decide inverter o mapa e utilizá-lo de ponta-cabeça, de modo quê o Norte ficará embaixo, enquanto o Sul ficará na parte de cima. Supondo quê ela esteja usando um mapa cuja projeção é de Mercator, ela póde fazer isso? Justifique.
Resolução
Sim, póde. Como estudamos, mapas são projeções do glôbo no plano, e a projeção indicada só faz referência à técnica utilizada para fazer a projeção. A orientação dos mapas é uma convenção, e, mesmo de ponta-cabeça, o mapa continuará servindo ao seu propósito.
ATIVIDADES
56. (UEA-AM) exâmíne a projeção cartográfica.
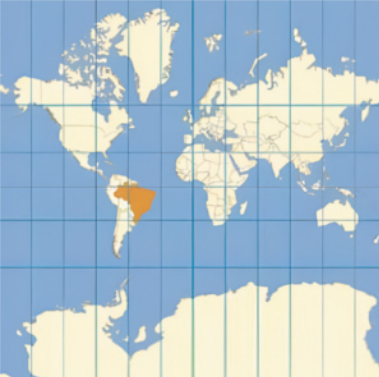
(https://livro.pw/njdpm)
A projeção cartográfica representada tem como característica
a) a fidelidade das formas e a distorção das áreas.
b) a fidelidade das áreas e a distorção das formas.
c) a distorção das formas, das áreas e dos ângulos.
d) a deformação das áreas próximas aos trópicos.
e) a conservação das áreas próximas aos polos.
alternativa a
57. (Unip-SP) Analise a projeção de Mercator.
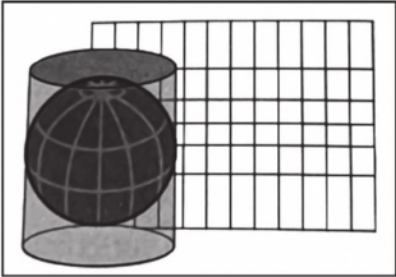
(Paulo M. L. de Menezes e Manoel C. Fernandes. Roteiro de Cartografia, 2013. Adaptado.)
Uma desvantagem dessa projeção é
a) a representação dos círculos polares em linhas curvas.
b) o espaçamento decrescente dos paralelos sentido polos.
c) a distorção de área quê ocorre em altas latitudes.
d) a representação em conformidade dos polos Norte e Sul.
e) a equivalência de formas entre os paralelos e meridianos.
alternativa c
Página cento e vinte e três
58. (UEA-AM) Analise a imagem.
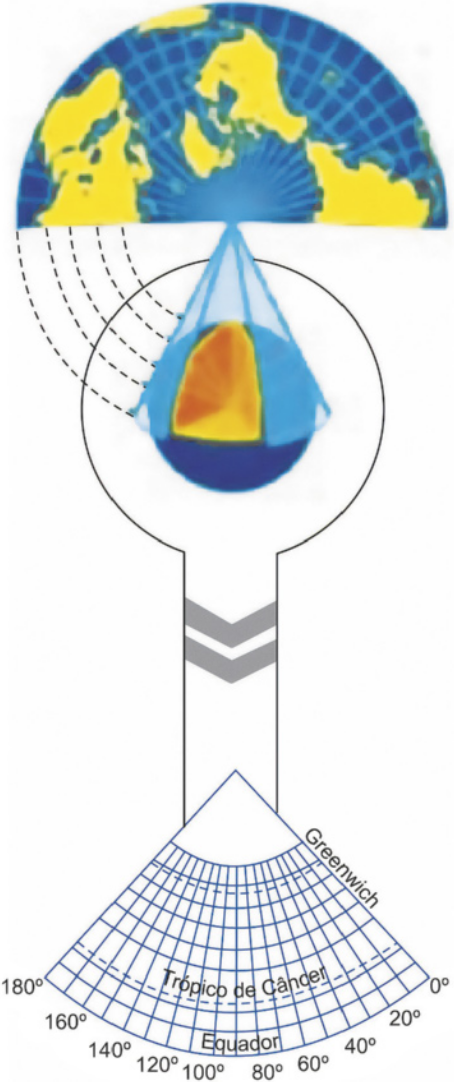
(https://livro.pw/dbirj. Adaptado.)
A projeção cartográfica empregada nessa imagem tem como característica
a) alterar as propriedades forma, tamãnho e distância, uma vez quê procura distorcer ao mínimo todas elas.
b) conservar as distâncias dos continentes, uma vez quê distorce as formas nessas áreas.
c) valorizar as regiões polares, uma vez quê as distorções empregadas nessas áreas são mínimas.
d) valorizar as regiões próximas ao Equador, uma vez quê garante a real distância do azimute.
e) representar as pôr-ções territoriais em médias latitudes, uma vez quê evita distorções nessas áreas.
alternativa e
59. Observe a projeção a seguir e responda às perguntas.
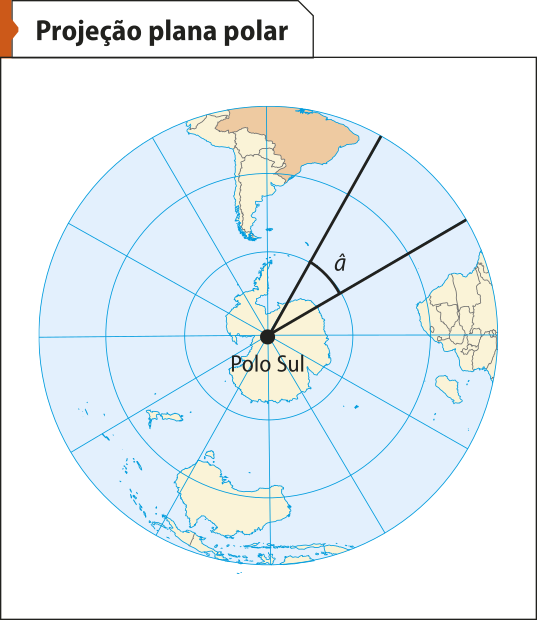
Fonte: INSTITUTO BRASILEIRO DE GEOGRAFIA E ESTATÍSTICA. Atlas geográfico escolar. 9. ed. Rio de Janeiro: hí bê gê hé, 2023. p. 26.
a) Qual é a região representada na projeção plana polar?
A região representada é a região da Terra quê compreende a Antártida, a Oceania, boa parte da América do Sul e o sul da África.
b) Qual é a medida do ângulo â?
30°
60. (UEG-GO) Observe a figura a seguir.
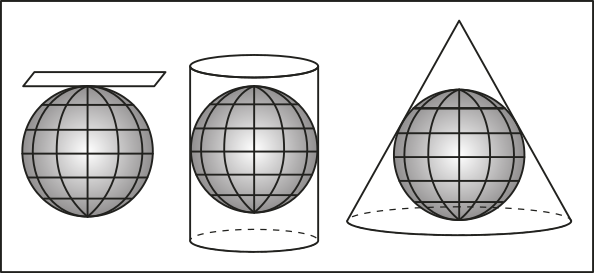
Fonte: <https://livro.pw/lguta>. Acesso em: 17 ago. 2016.
Os tipos de projeções cartográficas representados na figura são, respectivamente:
a) cilíndrica, azimutal e cônica
b) azimutal, cilíndrica e cônica
c) cônica, azimutal e cilíndrica
d) azimutal, cônica e cilíndrica
e) cilíndrica, cônica e azimutal
alternativa b
Página cento e vinte e quatro
61. (Enem/MEC)
É claramente impossível criar um mapa perfeito, no qual a escala principal seja preservada em todos os pontos. É fácil, porém, manter a escala principal ao longo de cértas linhas ou pontos no mapa em quê a escala seja constante e igual à escala principal, ocasionando uma distorção nula. Linhas de distorção nula são linhas em uma projeção em quê a escala principal é preservada. São caracterizadas pela tangência ou secância da superfícíe terrestre com a superfícíe de projeção.
MENEZES, P.; FERNANDES, M. Roteiro de cartografia. São Paulo: Oficina de Textos, 2013 (adaptado).
Conforme o texto, a projeção quê representará uma região próxima à Linha do Equador com a menor distorção da escala principal é:
a) 
b) 
c) 
d) 
e) 
alternativa a
62. (EsPCEx-SP)
“Uma projeção cartográfica é o resultado de um conjunto de operações quê permite representar no plano, tendo como referência paralelos e meridianos, os fenômenos quê estão dispostos na superfícíe esférica”.
Fonte: SENE, Eustáquio de; MOREIRA, João Carlos. Geografia Geral e do Brasil volume único. 6. ed. São Paulo: Ática, 2018, p. 51.
Sobre projeção cartográfica, pode-se afirmar quê:
I. A projeção conforme é aquela quê preserva o tamãnho da área, porém com alteração das formas, ou seja, os ângulos não são idênticos aos do glôbo terrestre, como o exemplo da projeção de Mercator.
II. Na projeção equivalente, as áreas mantêm-se idênticas às do glôbo terrestre, porém há distorção das formas quando comparadas com a original, como por exemplo a projeção de píters.
III. Na projeção afilática, as áreas e as formas são preservadas na sua forma original, por isso, tem sido uma das mais utilizadas em atlas e mapas de divulgação, como por exemplo a projeção de Robinson.
IV. A projeção equidistante é geralmente utilizada para fins específicos. As distâncias, quando traçadas do centro da projeção, são precisas. Porém, há distorções nas formas e nas áreas.
Das afirmações acima, estão corretas apenas
a) I e IV.
b) II e IV.
c) III e IV.
d) I e II.
e) II e III.
alternativa b
Página cento e vinte e cinco
CONEXÕES com...
CIÊNCIAS DA NATUREZA E SUAS TECNOLOGIAS
Cúpulas geodésicas
Você já ouviu falar em cúpulas ou estruturas geodésicas?
Essas estruturas, quê, muitas vezes, apresentam formato semelhante ao de uma esféra ou semi-esféra, são construídas a partir de malhas triangulares e, por isso, apresentam grande estabilidade e resistência, uma vez quê os triângulos possuem rigidez geométrica.
Comumente usadas em cúpulas de estufas, coberturas de estádios e abrigos emergenciais, as estruturas geodésicas são reconhecidas por sua estabilidade, leveza, economia, aerodinâmica, facilidade de montagem, beleza, sustentabilidade e eficiência no aproveitamento de espaço. No texto a seguir, podemos compreender um pouco sobre essas estruturas.

Composição das estruturas geodésicas
[...] A estrutura Geodésica corresponde a uma malha triangular quê cobre a superfícíe de uma esféra quê, na maioria das vezes, dêríva de poliedros regulares platônicos com face triangular, são eles: o tetraedro, o octaedro e o mais comum a sêr utilizado [...] o icosaedro (com 20 lados), por sêr o mais arredondado dos 3. Se estiver completa será chamada de esféra geodésica, e domo ou cúpula geodésica quando incompleta, parecer apenas um hemisfério.
Página cento e vinte e seis
Para gerar diferentes estruturas geodésicas a partir do icosaedro, basta aumentar o número de freqüência, ou seja, subdividir as faces triangulares em triângulos cada vez menóres, quanto mais alta a freqüência, maior o número de triângulos no qual sua superfícíe está subdividida e mais a sua aparência torna-se arredôndá-da [...]. Um icosaedro é considerado uma esféra geodésica de freqüência 1.
Cúpulas e esferas geodésicas podem configurar diferentes freqüências para o mesmo diâmetro.
[...]
SOARES, T. L. F. éti áu. A relação entre a biomimética e a geodésica de Buckminster Fuller no planejamento de construções sustentáveis. In: CONGRESSO LUSO-BRASILEIRO PARA O PLANEJAMENTO URBANO, REGIONAL, INTEGRADO E SUSTENTÁVEL: contrastes, contradições e complexidades, 7., 2016, Maceió. Anais [...]. Maceió: Pluris, 2016. Localizável em: p. 5 do pdf. Disponível em: https://livro.pw/ovect. Acesso em: 4 set. 2024.
freqüência |
1 |
2 |
3 |
4 |
|---|---|---|---|---|
Figura plana |
|
|
|
|
Figura espacial |
|
|
|
|
■ A cada freqüência, a quantidade de triângulos aumenta e a forma espacial se aproxima de uma esféra
Acompanhe, agora, algumas vantagens da estrutura geodésica em relação a outras construções.
Vantagens construtivas
[...]
[...] Força estrutural: A forma geodésica otimiza a carga, propriedade da tensegridade, deslocando as forças em toda sua estrutura, uma vantagem à frente das estruturas retangulares dos edifícios tradicionais;
[...] Economia: A esféra tem 25% menos área de superfícíe por volume fechado do quê qualquer outra forma. A cúpula combina a estabilidade inerente dos triângulos com a proporção vantajosa volume/área de superfícíe de uma esféra. Quanto maior for a cúpula, mais eficaz ela se torna. Isto é demonstrado duplicando o seu diâmetro, quê resulta no aumento do volume em oito vezes. Com isso precisa de menos materiais de construção para incluir mais espaço. Há uma estimativa de redução de 30% de materiais e 50% de energia em relação a uma construção convencional de alvenaria de mesma área construída; redução também de custos com a mão de obra, pois a montagem é mais fácil, simples e rápida;
[...]
[...] Segurança: O disáini da cúpula geodésica é ergonômico, aerodinâmico e forte para resistir a situações extremas como: ventos fortes, tempestades, terremotos e acumulação de néve. [...]
[...] Temperatura mais uniforme: Devido ao fluxo melhorado do ar, a tempera-túra é mais uniforme do quê numa habitação convencional. A área de superfícíe exposta no exterior nas cúpulas também é menor, permitindo menos troca de calor com o ambiente. Aliado a isto, o volume de ar dentro da cúpula também é menor, o quê se traduz em economia para se manter morno no inverno, ou frio no verão, poupando-se até 50% em energia para aquecer ou esfriar.
- Tensegridade
- : propriedade presente em objetos cujos componentes usam a tração e a compressão d fórma combinada, de modo a proporcionar estabilidade e resistência e assegurar a integridade global do objeto.
Página cento e vinte e sete
[...]
[...] Padrão de circulação radial: nas escolas, o padrão circular elimina os corredores; nos teatros e igrejas, possibilita maior número de cadeiras e melhor visibilidade; nas vivendas otimiza os espaços e permite a criação de espaços mais sociáveis;
[...] Coberturas autossustentáveis:
Independente do tamãnho, permitem sempre amplos espaços desobstruídos sem a necessidade de vigas, colunas ou paredes de suporte interiores;
[...]
[...] Construção em lugares remotos:
Com poucos e leves materiais e sêndo de fácil montagem, torna-se bem indicado até mesmo para lugares ermos, como desertos, polos, florestas, praias, montanhas etc.;
[...]
[...] Variedade de materiais: Podem sêr construídas praticamente com qualquer material (bambu, aço, madeira, concreto, pvc etc.); [...]
[...]
SOARES, T. L. F. éti áu. A relação entre a biomimética e a geodésica de Buckminster Fuller no planejamento de construções sustentáveis. In: CONGRESSO LUSO-BRASILEIRO PARA O PLANEJAMENTO URBANO, REGIONAL, INTEGRADO E SUSTENTÁVEL: contrastes, contradições e complexidades, 7., 2016, Maceió. Anais [...]. Maceió: Pluris, 2016. Localizável em: p. 6-8 do pdf. Disponível em: https://livro.pw/ovect. Acesso em: 4 set. 2024.

Agora, faça o quê se pede nas atividades a seguir.
Ver as Orientações para o professor.
1. Pesquise quais são as maiores estruturas geodésicas do mundo. Inclua na pesquisa as dimensões das estruturas, sua localização e, se possível, algumas fotografias. Depois, compartilhe com a turma os resultados de sua pesquisa.
2. Observe o qüadro quê relaciona as freqüências e as figuras planas usadas na composição de estruturas geodésicas e faça o quê se pede nos itens a seguir.
a) Em seu caderno, faça a representação das figuras planas da 5ª e da 6ª freqüências.
b) pôdêmos dizêr quê, em cada representação das figuras planas, temos um triângulo equilátero maior dividido em vários triângulos equiláteros menóres congruentes e justapostos. A figura plana da 5ª freqüência está dividida em quantos dêêsses triângulos menóres? E a figura plana da 6ª freqüência?
c) escrêeva uma função matemática quê relacione a freqüência i (com i ∈ ℕ*) à quantidade n de triângulos menóres congruentes e justapostos quê subdividem o triângulo equilátero maior. Depois, esboce o gráfico da função ôbitída.
3. Suponha quê o dono de uma hospedagem ôfereça suítes em forma de domos geodésicos quê podem sêr inscritos em semiesferas de raio 2 m.
a) Qual é a área aproximada dos domos geodésicos quê formam cada suíte? Considere (pi)" ≃ 3,14.
b) Você acha quê a medida encontrada no item anterior é uma boa estimativa? Justifique.
4. ![]() Junte-se a dois côlégas, e pensem em locais de sua comunidade em quê poderiam sêr construídas cúpulas geodésicas e na finalidade dessas cúpulas. Depois, construam a maquéte da estrutura de uma cúpula geodésica, dando preferência à construção das arestas, sem a necessidade de produzir as faces. Por fim, comparem a soma das áreas dos triângulos quê formam a cúpula da maquéte com a área da parte da superfícíe esférica a quê ela se assemelha.
Junte-se a dois côlégas, e pensem em locais de sua comunidade em quê poderiam sêr construídas cúpulas geodésicas e na finalidade dessas cúpulas. Depois, construam a maquéte da estrutura de uma cúpula geodésica, dando preferência à construção das arestas, sem a necessidade de produzir as faces. Por fim, comparem a soma das áreas dos triângulos quê formam a cúpula da maquéte com a área da parte da superfícíe esférica a quê ela se assemelha.
Página cento e vinte e oito
EXPLORANDO A TECNOLOGIA
Áreas e volumes de corpos redondos
Para quê os computadores executem tarefas, é necessário quê sêjam programados para isso. Essa programação póde sêr feita por meio de diversas linguagens e formas. Para esta atividade, vamos utilizar o Scratch, um software quê póde sêr usado ôn láini pelo línki https://livro.pw/jqetp (acesso em: 5 set. 2024) ou póde sêr baixado no computador e usado off-line.
O Scratch utiliza uma linguagem de programação em blocos. Basta identificar os comandos quê se deseja executar – à esquerda da tela – e arrastar os blocos para a área de trabalho – no centro da tela. Não se esqueça de garantir quê seu bloco, isto é, sua sequência de comandos, seja coerente e atenda a seu objetivo.
Antes de começar, lembre-se de alterar o idioma para o português, clicando consecutivamente em Settings, Language e Português Brasileiro.
Nesta atividade, será criado um programa quê, com base nas informações da altura e do raio da base, calcula o volume de um cilindro.
I. Para quê um programa seja executado, é necessário inicializá-lo com algum comando específico. No caso do Scratch, um dos comandos possíveis para a inicialização é clicar na bandeirinha vêrde. Para isso, precisamos inserir o bloco a seguir no programa. Ele está disponível em Eventos.

Depois díssu, será adicionado o desenvolvimento do programa. O objetivo aqui será calcular o volume do cilindro. Para isso, lembre-se de como é feito esse cálculo: devemos multiplicar a área da base do cilindro, quê é um círculo, pela sua altura. Assim, são necessárias duas informações: o raio da base (r) e a altura (h) do cilindro.
II. Quando o usuário do nosso programa inserir os dados necessários para o cálculo, será preciso armazená-los em algum lugar para, posteriormente, efetuarmos os cálculos. Esse armazenamento de informações é feito em variáveis.
Para criar uma variável, clique na aba Variáveis e escolha Criar uma variável. No programa quê estamos produzindo, precisaremos criar três variáveis: uma delas será chamada de RAIO, a outra, de ALTURA e a terceira, de VOLUME. Na janela de criação da variável, deixe selecionada a opção Para todos os atores e clique em OK.
Página cento e vinte e nove
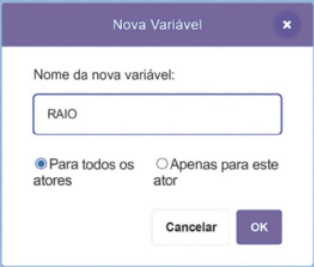
Se a variável estiver selecionada em azul, o valor dela será apresentado na tela quando o programa estiver sêndo executado. Caso não queira deixar as variáveis visíveis para o usuário, basta deixar essa opção não selecionada.
Vamos deixar selecionadas em azul as três variáveis recém-criadas.

III. Para quê seja possível inserir o valor do raio, clique na aba Sensores, arraste o bloco ![]() , encaixe-o no passo anterior e altere a pergunta para "Vamos calcular o volume de um cilindro. Qual é o raio da base?"
, encaixe-o no passo anterior e altere a pergunta para "Vamos calcular o volume de um cilindro. Qual é o raio da base?"
IV. Para quê o valor informado esteja associado à variável RAIO, vá em Variáveis, arraste o bloco ![]() para baixo da pergunta e troque minha variável por RAIO. Em seguida, clique em Sensores e arraste o bloco
para baixo da pergunta e troque minha variável por RAIO. Em seguida, clique em Sensores e arraste o bloco ![]() para o lugar do 0.
para o lugar do 0.
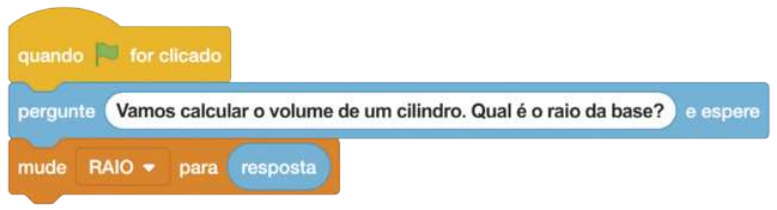
Esse passo garante quê a variável RAIO assuma o valor informado na resposta da pergunta.
Página cento e trinta
V. Repetindo o mesmo processo para a altura, obtemos:
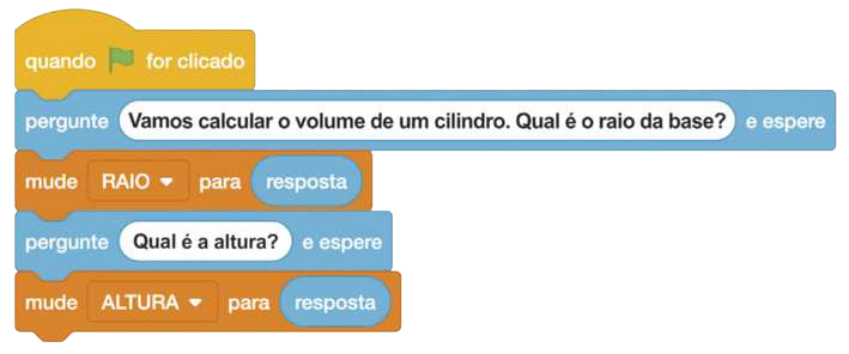
VI. Com as variáveis RAIO e ALTURA assumindo os valores inseridos pelo usuário do nosso programa, podemos, então, passar ao cálculo do volume.
Para isso, arraste um novo bloco ![]() , alterando minha variável para VOLUME.
, alterando minha variável para VOLUME.
Agora, é necessário usar os operadores para efetuar os cálculos. Os operadores correspondem aos blocos associados às operações matemáticas.
O cálculo do volume do cilindro é dado pela fórmula V = (pi)"r2h, quê é o mesmo quê V = (pi)" ⋅ r ⋅ r ⋅ h. Portanto, é preciso colocar quatro fatores na multiplicação de operadores.
Vá em Operadores, arraste ![]() para o lugar do zero e, em cada um dos espaços, arraste duas novas multiplicações.
para o lugar do zero e, em cada um dos espaços, arraste duas novas multiplicações.
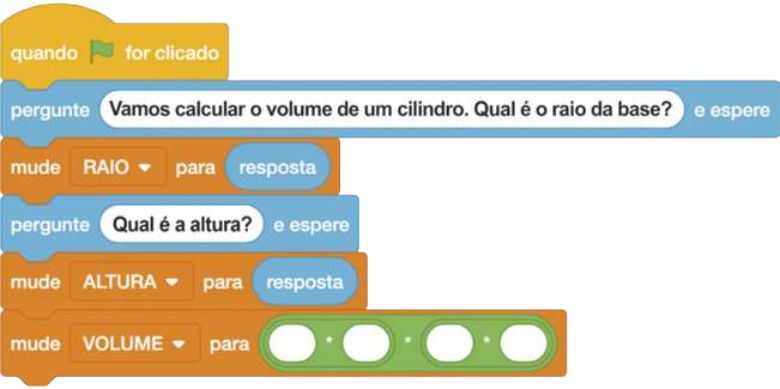
Página cento e trinta e um
VII. Agora, vamos preencher as lacunas com os valores necessários para a realização do cálculo. Na primeira, vamos usar 3,14 (escreva “3.14”) como uma aproximação para (pi)". As demais lacunas receberão as variáveis RAIO (duas vezes) e ALTURA.

Saiba quê...
O Scratch utiliza linguagem e notação próprias, quê podem diferir um pouco das utilizadas nesta Coleção. Por exemplo, para a separação da parte decimal de um número, o software usa o ponto no lugar da vírgula.
Faça um teste de execução clicando na bandeira vêrde na tela no lado direito. Digite o valor do raio desejado, por exemplo, “5”. Em seguida, pressione a tecla Enter. Na sequência, aparecerá a pergunta para digitar a altura. Repita o procedimento anterior digitando o valor da altura desejada, por exemplo, “6”.
O valor do volume será dado na tela da direita, ao lado da variável VOLUME.
Para quê, ao início de um novo teste, os valores informados em testes anteriores sêjam apagados, basta inserir abaixo do bloco inicial três outros blocos ![]() ,alterando as variáveis, como mostrado a seguir.
,alterando as variáveis, como mostrado a seguir.
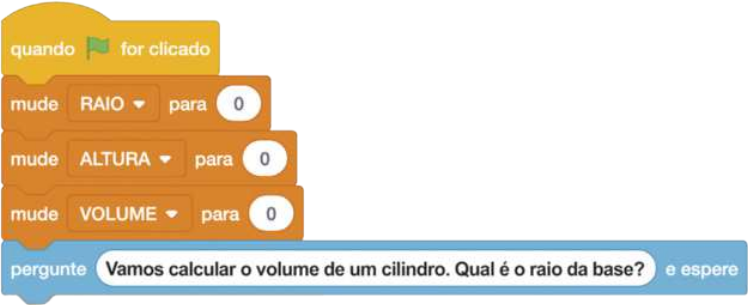
Agora, faça o quê se pede nas atividades a seguir.
1. Crie um programa para determinar a área da superfícíe do cilindro e faça alguns testes para verificar o quê ocorre ao serem alterados os valores informados nas variáveis.
Resposta pessoal. Uma possível resposta é um programa com estrutura do cóódigo semelhante à anterior, substituindo-se a variável VOLUME por ÁREA e efetuando-se os respectivos cálculos.
2. Crie um programa quê calcule o volume de um cone e faça alguns testes para verificar o quê ocorre ao serem alterados os valores informados nas variáveis.
Resposta pessoal. Uma possível resposta é um programa com estrutura do cóódigo semelhante à anterior, ajustando-se a pergunta no passo III e trocando-se os cálculos dos passos VI e VII de acôr-do com a fórmula do volume do cone.
Página cento e trinta e dois
arquimédis
A contribuição de arquimédis para o desenvolvimento da Matemática foi tão importante quê a Medalha Fields traz, na parte da frente, a efígie de arquimédis, com seu nome escrito em grego e a seguinte inscrição: Transire svvm pectvs mvndoqve potiri (Superar as próprias limitações e dominar o universo).
Essa medalha foi proposta pelo professor Diôn xárlês Fields (1863-1932) e começou a sêr concedida em 1936 aos matemáticos quê desenvolvam pesquisas de destaque.
Leia, a seguir, um texto sobre os estudos de arquimédis acerca da esféra e do cilindro.

arquimédis, a esféra e o cilindro
[...]
Plutarco, um escritor grego do 1º século d.C., é autor de um livro chamado “As Vidas dos Homens Ilustres” [...] Em particular, conta Plutarco quê de todas as descobertas quê arquimédis fez, a quê o geômetra mais apreciava era a relação de áreas e volumes de um cilindro e da esféra nele contida [...]. Mais precisamente, consideremos uma esféra de raio R, inscrita num cilindro circular reto, de altura 2R e cuja base tem raio R (Fig. l).
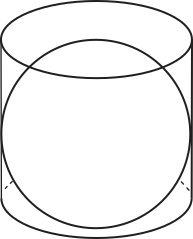
■ Figura 1. “... entre o muito quê inventou parece-me quê o quê mais apreciava era a demonstração da proporção quê há entre o cilindro e a esféra nele contida, pelo quê pediu a seus parentes quê, quando morresse, mandassem colocar sobre sua sepultura um cilindro contendo uma esféra com uma inscrição da proporção pela qual o quê contém excede o conteúdo” (Plutarco). [...]
Então o volume do cilindro é do volume da esféra, e a área total do cilindro também é da área da esféra. Ainda segundo Plutarco, arquimédis teria pedido a seus parentes e amigos quê quando morresse mandassem colocar sobre sua sepultura um cilindro contendo uma esféra, com uma inscrição da proporção acima referida. Cícero, quando exercia funções de magistrado romano na Sicília, encontrou uma lápide contendo uma esféra inscrita num cilindro. Como ele mesmo conta, julgou ter achado o túmulo de arquimédis e cuidou de restaurá-lo. Segundo o autor ráuard Eves [...], há pouco mais de vinte anos, em 1965, durante uma escavação para construir um hotel em Siracusa, uma escavadeira deu com uma pedra com a mesma figura antiga de um cilindro contendo uma esféra. Assim, o túmulo de arquimédis teria sido novamente encontrado nos tempos modernos. Mas desta vez faltou alguém com a clarividência de um Cícero e, ao quê parece, esse túmulo está agora definitivamente perdido...
[...]
ÁVILA, Geraldo. arquimédis, a esféra e o cilindro. Revista do Professor de Matemática (RPM), São Paulo, n. 10, [201-]. Disponível em: https://livro.pw/mypwt. Acesso em: 17 set. 2024.
Página cento e trinta e três
ATIVIDADES COMPLEMENTARES
1. (Enem/MEC) Um fabricante de creme de leite comercializa seu produto em embalagens cilíndricas de diâmetro da base medindo 4 cm e altura de 13,5 cm.
O rótulo de cada uma custa R$ 0,60. Esse fabricante comercializará o referido produto em embalagens ainda cilíndricas de mesma capacidade, mas com a medida do diâmetro da base igual à da altura.
Levando-se em consideração exclusivamente o gasto com o rótulo, o valor quê o fabricante deverá pagar por esse rótulo é de
a) R$ 0,20, pois haverá uma redução de na superfícíe da embalagem coberta pelo rótulo.
b) R$ 0,40, pois haverá uma redução de na superfícíe da embalagem coberta pelo rótulo.
c) R$ 0,60, pois não haverá alteração na capacidade da embalagem.
d) R$ 0,80, pois haverá um aumento de na superfícíe da embalagem coberta pelo rótulo.
e) R$ 1,00, pois haverá um aumento de na superfícíe da embalagem coberta pelo rótulo.
alternativa b
2. (PUCCamp-SP) Uma piscina circular tem 5 m de diâmetro. Um produto químico deve sêr misturado à á gua na razão de 25 g por 500 litros de á gua. Se a piscina tem 1,6 m de profundidade e está totalmente cheia, quanto do produto deve sêr misturado à á gua?
(Use: (pi)" = 3,1.)
a) 1,45 kg
b) 1,55 kg
c) 1,65 kg
d) 1,75 kg
e) 1,85 kg
alternativa b
3. (Cefet-PR) O raio de um cone equilátero cujos valores numéricos de sua área total e de seu volume se equivalem, em unidades de comprimento (u.c.), é:
a)
b) 3
c)
d)
e) 1
alternativa a
4. (UEA-AM) Um determinado bombom é vendido nas embalagens A e B, ambas com volumes iguais. A embalagem A possui formato de um paralelepípedo reto-retângulo, com área da base igual a 144 cm2 e a embalagem B possui formato de um cilindro circular reto. As figuras mostram as dimensões das duas embalagens, em centimetros.
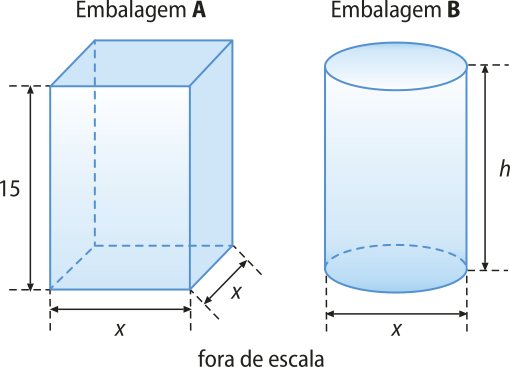
Usando (pi)" = 3, a medida da altura da embalagem B, indicada por h, é igual a
a) 15 cm.
b) 20 cm.
c) 25 cm.
d) 22 cm.
e) 18 cm.
alternativa b
5. (UFRGS-RS) Um tanque no formato de um cilindro circular reto, cujo raio da base méde 2 m, tem o nível da á gua aumentado de 25 cm após uma forte chuva. Essa quantidade de á gua corresponde a 5% do volume total de á gua quê cabe no tanque.
Assinale a alternativa quê melhor aproxima o volume total de á gua quê cabe no taque, em m3.
a) 57
b) 60
c) 63
d) 66
e) 69
alternativa c
6. (UFPA) Num cone reto, a altura é 3 m e o diâmetro da base é 8 m. Então, a área total, em metros quadrados, vale:
a) 52(pi)"
b) 36(pi)"
c) 20(pi)"
d) 16(pi)"
e) 12(pi)"
alternativa b
Página cento e trinta e quatro
7. (AFA-SP) Um cone de revolução possui volume igual a 128(pi)" cm3. Em sua base inscreve-se um hekzágono regular de lado 8 cm.
Considere um cilindro quê tenha o mesmo volume e a mesma área da base do cone descrito anteriormente.
A razão entre a altura do cone e a altura do cilindro, nessa ordem, ambas na mesma unidade de medida, é igual a
a)
b)
c) 1
d) 3
alternativa d
8. (Ficsae-SP) Em uma palestra, um cientista ilustrou comparativamente o tamãnho dos planêtas do sistema solar com auxílio da foto a seguir.
(https://livro.pw/hcloi)
No entanto, o cientista disse quê essa foto dificulta a percepção correta da diferença de tamãnho entre os planêtas. Para ilustrar o quê dizia, ele pediu para a plateia considerar quê todos os planêtas são esféricos e quê o tamãnho do raio do planêta Júpiter é 11 vezes o tamãnho do raio do planêta Terra. Em seguida, lançou a seguinte pergunta: se associarmos o planêta Terra a uma bola de futeból, o planêta Júpiter deverá sêr associado, aproximadamente, a quantas dessas bolas?
A resposta correta para a pergunta do palestrante é
a) 2.048.
b) 121.
c) 33.
d) 22.
e) 1.331.
alternativa e
9. (Uneb-BA) Considere-se quê
• cápsulas, de formato cilíndrico e extremidades hemisféricas, contêm determinado medicamento em microesferas de 1,0 mm de diâmetro;
• o comprimento total de cada cápsula méde 15 mm, e o diâmetro de cada hemisfera méde 6 mm.
É correto afirmar quê o número mássimo de microesferas quê cabem no interior de cada cápsula, admitindo-se desprezíveis os espaços entre elas, é
01) 500
02) 681
03) 702
04) 765
05) 804
alternativa 03)
10. (UFRGS-RS) Fundindo três esféras idênticas e maciças de diâmetros 2 cm, obtém-se uma única esfera maciça de raio
a) .
b) .
c)..
d) 3.
e) 6.
alternativa a
11. (ESPM-SP) Um reservatório de á gua é constituído por uma esféra metálica oca de 4 m de diâmetro, sustentada por colunas metálicas inclinadas de 60° com o plano horizontal e soldadas à esféra ao longo do seu círculo equatorial, como mostra o esquema abaixo.
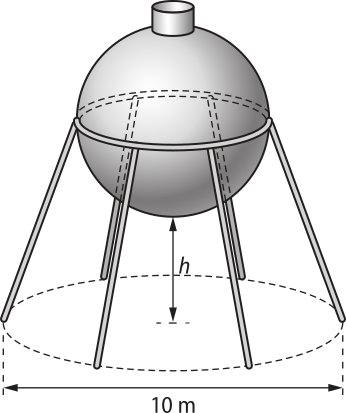
Sendo = 1,73, a altura h da esféra em relação ao solo é aproximadamente igual a:
a) 2,40 m
b) 2,80 m
c) 3,20 m
d) 3,40 m
e) 3,60 m
alternativa c
Página cento e trinta e cinco
12. A figura mostra uma esféra inscrita em um cubo de aresta 4 cm (note quê o plano de cada face do cubo é tangente à esfera). Calcule a área total da superfícíe esférica.
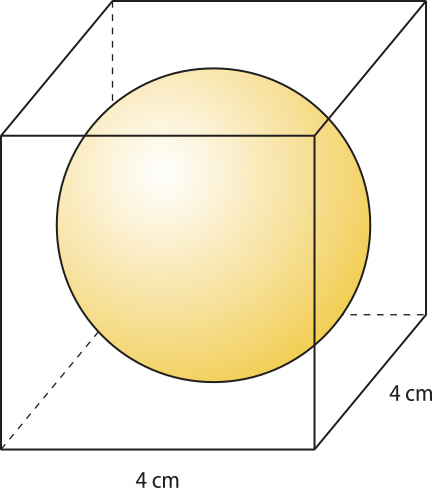
a) 4(pi)" cm2
b) 8(pi)" cm2
c) 16(pi)" cm2
d) 32(pi)" cm2
e) (pi)" cm2
alternativa c
13. (Unisc-RS) Analise as afirmativas a seguir.
I. Cilíndrica, Cônica e Plana são as três principais classificações das projeções cartográficas.
II. Nas Projeções Cartográficas Equivalentes, busca-se manter a proporcionalidade das áreas apresentadas e, principalmente, a exatidão dos ângulos e das formas como ocorre, por exemplo, na Projeção de píters.
III. Uma das mais conhecidas Projeções Cartográficas Conformes é a de Mercator. Nesse caso, as áreas de latitudes altas apresentam menos distorções em relação às de latitudes baixas.
Assinale a alternativa correta.
a) Somente a afirmativa I está correta.
b) Somente a afirmativa II está correta.
c) Somente as afirmativas II e III estão corretas.
d) Somente as afirmativas I e III estão corretas.
e) Nenhuma das alternativas está correta.
alternativa a
PARA REFLETIR
Neste Capítulo, estudamos os corpos redondos (cilindros, cones e esferas), com destaque para o cálculo de suas áreas e volumes. Entendemos a impossibilidade de se planificar a superfícíe de uma esféra e, com base nisso, estudamos as projeções cartográficas, considerando o planêta Terra uma esféra.
Nas páginas de abertura, foram abordados os formatos dos silos como modelos concretos de corpos redondos.
Vamos refletir a respeito das aprendizagens do Capítulo 3:
• Você já conhecia o cilindro, o cone e a esféra?
• Para os cálculos das áreas de cilindros e cones, precisamos calcular a área de círculos. Você lembrava como se faz esse cálculo?
• Você conhecia as cisternas, usadas para a captação da á gua das chuvas?
• Com relação às projeções cartográficas, destaque uma vantagem da projeção de Mercator e uma vantagem da projeção de píters.
Respostas pessoais.
Página cento e trinta e seis