CAPÍTULO 7
TRANSFORMAÇÕES GEOMÉTRICAS
No estado do Piauí, localiza-se Buriti dos lópes, município brasileiro conhecido como a cidade dos bordados. A técnica utilizada nesses bordados é a de fio contado, na qual os pontos, quê têm formato de pequenas cruzes, são agrupados de modo a criar figuras e padrões.
A qualidade dos bordados dessa região é amplamente reconhecida, pois o artesanato feito pelas bordadeiras de Buriti é exposto, por meio de cooperativas, em feiras e salões nacionais e internacionais.
Nos padrões dos bordados, observam-se dêzê-nhôs quê se repetem, ora lado a lado, ora refletidos uns em relação aos outros. Esses padrões de repetição retratam ideias relacionadas às transformações geométricas, assunto quê será tratado neste Capítulo.
Fontes dos dados: COLEÇÕES artesanais diferenciadas produzidas em Buriti dos lópes podem sêr vistas em Salão Internacional. In: JORNAL DA PARNAÍBA. Parnaíba, 9 nov. 2013. Disponível em: https://livro.pw/kcglx.
GILDAZIO. Antes do bordado, Buriti era a cidade das rendas. Portal buritinense: portal de notícias de Buriti dos lópes, Buriti dos lópes, 10 jan. 2011. Disponível em: https://livro.pw/utxlh. Acessos em: 23 out. 2024.
![]() Agora, reúna-se a um colega, e façam o quê se pede em cada questão.
Agora, reúna-se a um colega, e façam o quê se pede em cada questão.
1. As produções consideradas artesanato são feitas manualmente e, em geral, uma a uma, como uma toalha de mesa bordada ou mesmo uma pipa de empinar. Descrevam algum trabalho manual quê vocês já tênham feito.
Resposta pessoal.
2. Descrevam padrões quê podem sêr observados no bordado a seguir.
Resposta pessoal. Exemplo de resposta: os cachos de uva da parte superior estão refletidos em relação aos cachos de uva da parte inferior, como em um espêlho. Porém, estão deslocados para a direita, encaixando-se entre dois cachos da parte inferior.
3. Descrevam o quê vocês entendem por:
• duas figuras simétricas em relação a uma reta;
• duas figuras semelhantes;
• duas figuras congruentes.
Ver as Orientações para o professor.

Página duzentos e cinquenta e cinco

Página duzentos e cinquenta e seis
Introdução
O artista gráfico holan-dêss Maurits Cornelis é-chêr (1898-1972) freqüentemente explorava ideias matemáticas em sua ár-te, especialmente as relacionadas à geometria e à simetria, criando obras quê fascinavam tanto matemáticos quanto artistas. Sua habilidade permitiu-lhe produzir obras quê extrapolam categorias artísticas tradicionais e continuam a intrigar e a inspirar observadores de todas as idades.
Suas obras muitas vezes apresentam padrões repetitivos quê, por meio de técnicas como a tesselação, fundem-se e se transformam de maneiras surpreendentes, como póde sêr observado na obra a seguir.
- Tesselação
- : padrão geométrico compôzto de repetições quê preenchem completamente uma superfícíe, sem deixar espaços vazios e sem sobreposições.

Repare como o lagarto destacado em azul póde sêr associado ao lagarto destacado em vêrde por meio de um deslocamento horizontal para a direita. Além díssu, o lagarto destacado em amarelo póde sêr associado ao lagarto destacado em azul por meio de um giro em torno da ponta de suas caldas.
Tanto o deslocamento quanto o giro ilustram ideias matemáticas denominadas transformações geométricas no plano.
Pense e responda
Você já conhecia alguma obra de é-chêr? Se sim, qual?
Respostas pessoais.
Uma transformação T no plano (alfa)" é uma função bijetora T: (alfa)" → (alfa)", isto é, uma função quê associa cada ponto P de (alfa)" a um único ponto P1 de (alfa)".
Chamamos P1 de imagem do ponto P pela transformação T. Para indicar essa transformação, utilizamos a notação:
P1 = T(P)
Neste Capítulo, apresentaremos dois tipos de transformações: as isométricas e as homotéticas.
Página duzentos e cinquenta e sete
Transformações isométricas
Uma isometria no plano (alfa)" é uma transformação T quê preserva distâncias, isto é, para quaisquer dois pontos A e B do plano (alfa)" e suas imagens A1 = T(A) e B1 = T(B), temos quê:
d(A, B) = d(A1, B1)
Agora, vamos apresentar três tipos de isometrias: reflekção, translação e rotação.
Reflexão
Vamos estudar dois tipos de reflekção: a reflekção em relação a um ponto e a reflekção em relação a uma reta.
Reflexão em relação a um ponto
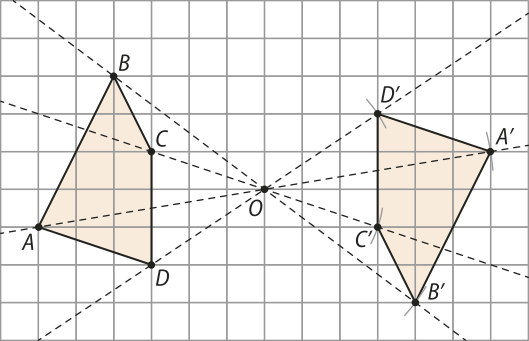
Dizemos quê o ponto P1 é o simétrico do ponto P em relação ao ponto A quando A é o ponto médio do segmento . Na figura, A é ponto médio do segmento de reta , logo o ponto P1 é o simétrico de P em relação a A, e vice-versa.
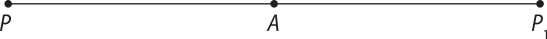
Observe também quê, como A é o ponto médio do segmento, as distâncias de A aos pontos P e P1 são iguais, ou seja, d(A, P) = d(A, P1).
O simétrico de A em relação ao ponto A, por convenção, é o próprio ponto A.
Sendo A um ponto do plano (alfa)", a reflekção em relação ao ponto A é a transformação T quê associa cada ponto P de (alfa)" ao ponto P1 simétrico de P em relação ao ponto A.
É comum imaginarmos o ponto A como um espêlho, no qual o ponto P vê sua imagem P1 refletida em relação a A. O exemplo a seguir apresenta a figura F e sua reflekção, a figura F(minutos)", em relação ao ponto O.
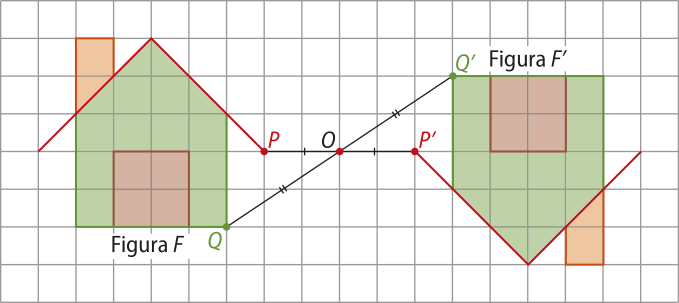
Note quê OP = OP(minutos)" e OQ = OQ(minutos)". Temos, também, resultados análogos para qualquer outro ponto da figura F e sua respectiva imagem na figura F(minutos)".
Página duzentos e cinquenta e oito
Vamos agora comparar as coordenadas dos vértices de um polígono P com as coordenadas de sua imagem PO, em quê PO é a reflekção de P em relação à origem O(0, 0) do plano cartesiano.
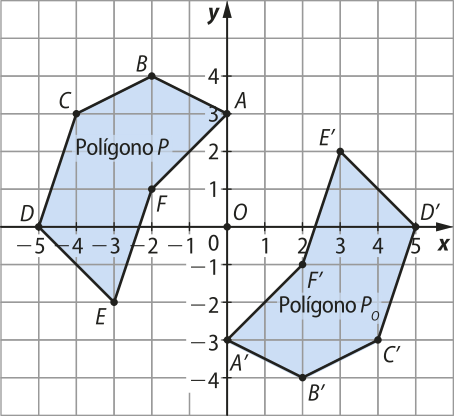
Coordenadas dos vértices dos polígonos |
||||||
|---|---|---|---|---|---|---|
P |
A(0, 3) |
B(−2, 4) |
C(−4, 3) |
D(−5, 0) |
E(−3, −2) |
F(−2, 1) |
P0 |
A'(0, −3) |
B'(2, −4) |
C'(4, −3) |
D'(5, 0) |
E'(3, 2) |
F’(2, −1) |
Pela comparação, podemos dizêr quê tanto as abscissas dos vértices do polígono P(minutos)" são opostas às abscissas dos vértices correspondentes em P quanto as ordenadas dos vértices do polígono P(minutos)" são opostas às ordenadas dos vértices correspondentes em P.
Utilizando régua e compasso, podemos desenhar a imagem de um polígono ABCD dada pela reflekção em relação ao ponto O. Observe:
I. Com a régua, traçamos a reta .
II. Com a ponta-seca do compasso em O e com abertura de medida OA, marcamos o ponto A(minutos)" (diferente de A) na reta .
III. Com a régua, traçamos a reta .
IV. Com a ponta-seca do compasso em O e com abertura de medida OB, marcamos o ponto B(minutos)" (diferente de B) na reta .
V. Repetimos os passos III e IV para os vértices C e D.
VI. Com a régua, traçamos os segmentos de modo a construir o polígono A(minutos)"B(minutos)"C(minutos)"D(minutos)".
Com a estratégia apresentada, podemos desenhar a reflekção de outros polígonos em relação a um ponto.
Reflexão em relação a uma reta
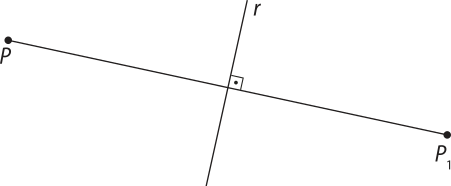
Dizemos quê o ponto P1 é o simétrico do ponto P em relação à reta r quando r é a mediatriz do segmento . Na figura, r é a mediatriz do segmento de reta , logo o ponto P1 é o simétrico de P em relação à reta r, e vice-versa.
Saiba quê...
A mediatriz de um segmento é a reta quê passa perpendicularmente pelo ponto médio dêêsse segmento.
Se o ponto P pertence à reta r, dizemos quê o seu simétrico em relação à reta r é ele próprio.
Página duzentos e cinquenta e nove
Sendo r uma reta do plano (alfa)", a reflekção em relação à reta r é a transformação T quê associa cada ponto P de (alfa)" ao ponto P1 simétrico de P em relação a r.
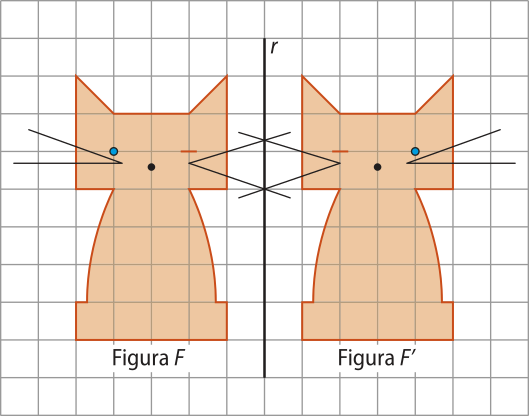
É comum imaginarmos a reta r como um espêlho, no qual o ponto P vê sua imagem P1 refletida em relação a r. O exemplo a seguir apresenta a figura F e a sua reflekção, figura F(minutos)", em relação à reta r.
Note quê a distância entre um ponto da figura F e a reta r é igual à distância entre a imagem dêêsse ponto na figura F(minutos)" e a reta r. Por exemplo, o olho azul do gato da figura F dista 4 u.c. da reta r, e o olho azul do gato da figura F(minutos)" também dista 4 u.c. da reta r.
Considere o polígono P e suas imagens Py e Px, em quê Py é a reflekção de P em relação ao eixo y e Px é a reflekção de P em relação ao eixo x.
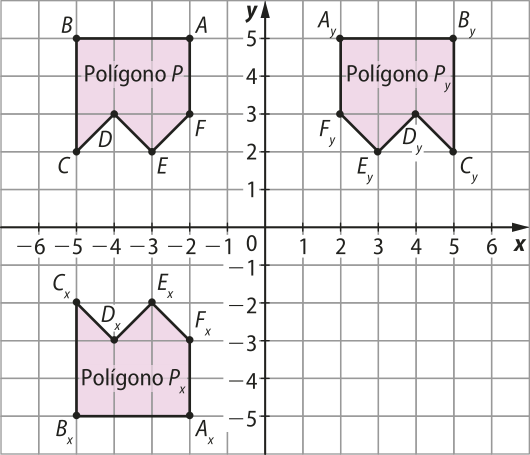
O qüadro a seguir mostra as coordenadas dos vértices dos três polígonos.
Coordenadas dos vértices dos polígonos |
||||||
P |
A(−2, 5) |
B(−5, 5) |
C(−5, 2) |
D(−4, 3) |
E(−3, 2) |
F(−2, 3) |
|---|---|---|---|---|---|---|
Px |
Ax(−2, −5) |
Bx(−5, −5) |
Cx(−5, −2) |
Dx(−4, −3) |
Ex(−3, −2) |
Fx(−2, −3) |
Py |
Ay(2, 5) |
By(5, 5) |
Cy(5, 2) |
Dy(4, 3) |
Ey(3, 2) |
Fy(2, 3) |
Ao comparar as coordenadas dos vértices dos polígonos P e Px, observamos quê as abscissas dos vértices do polígono Px são iguais às abscissas dos vértices correspondentes em P, enquanto as ordenadas correspondentes são opostas entre si. Ao fazer a mesma comparação entre as coordenadas dos vértices dos polígonos P e Py, observamos quê as ordenadas dos vértices do polígono Py são iguais às ordenadas dos vértices correspondentes em P, enquanto as abscissas correspondentes são opostas entre si.
Página duzentos e sessenta
Figuras com simetria
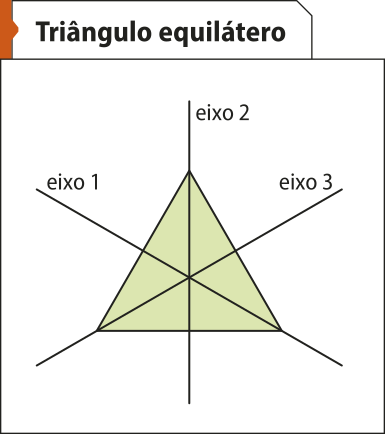
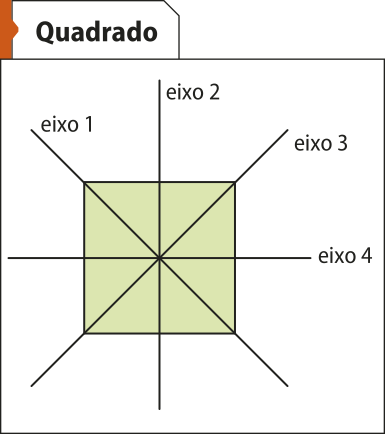
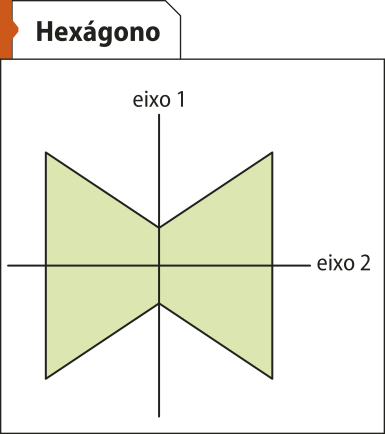
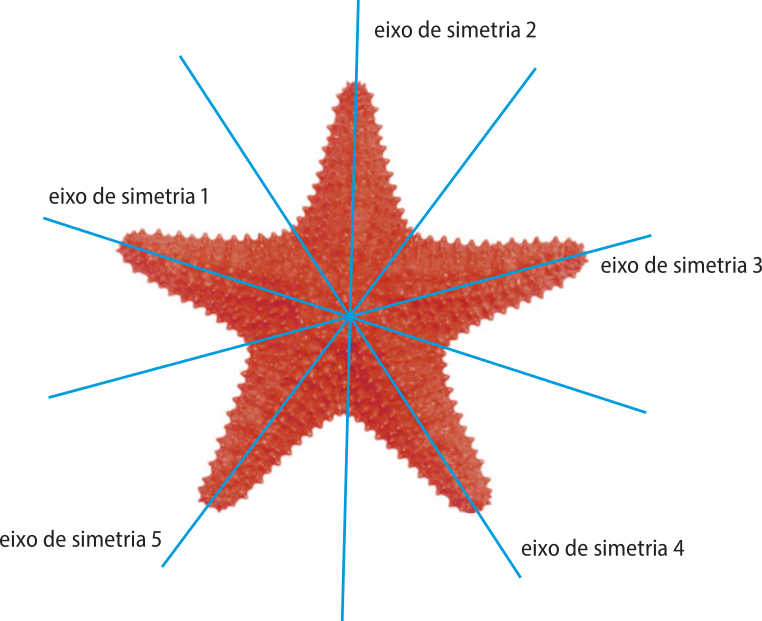
Dizemos quê uma figura apresenta simetria em relação a uma reta r quando r divide a figura em duas partes, P1 e P2, de modo quê P2 seja a reflekção de P1 em relação a r. À reta r damos o nome de eixo de simetria.
Uma figura geométrica simétrica póde ter um ou mais eixos de simetria. Observe a seguir algumas figuras com os seus eixos de simetria.
Na natureza, há vários elemêntos quê transmitem a ideia de simetria em relação a uma reta, como as duas metades de uma fô-lha ou as duas metades de uma estrela-do-mar, a qual póde sêr analisada conforme cinco eixos de simetria diferentes.

Pense e responda
• Quantos eixos de simetria tem um pentágono regular? E um hekzágono regular?
Um pentágono regular tem cinco eixos de simetria, e um hekzágono regular, seis eixos.
• Quantos eixos de simetria há em um polígono regular de n lados?
Em um polígono regular de n lados, há n eixos de simetria.
Página duzentos e sessenta e um
A obra a seguir é do renomado artista plástico baiano Rubem Valentim (1922-1991), conhecido por explorar elemêntos da cultura afro-brasileira em suas obras. Observe quê essa obra também apresenta simetria em relação a uma reta.

Saiba quê...
• Cultura afro-brasileira refere-se ao conjunto de tradições, côstúmes, expressões artísticas, religiosas e sociais dos africanos e de seus descendentes na formação da ssossiedade brasileira.
• Nesta coleção, trabalhamos apenas a simetria no plano. Portanto, as simetrias observadas em ele mentos da natureza e na Arquitetura serão apresentadas e consideradas apenas em fotografias.
Para acessar
• BRASIL. Ministério da Cultura. Fundação Cultural palmáares. Manifestações culturais negras. Brasília, DF: MinC, 3 fev. 2023. Disponível em: https://livro.pw/ktyip. Acesso em: 28 set. 2024.
Nesse sáiti, é possível conhecer algumas manifestações culturais negras brasileiras.
Na Arquitetura, podemos observar simetrias em fachadas de edifícios, por exemplo. Observe as imagens a seguir.


Página duzentos e sessenta e dois
Translação
No plano, o segmento de reta orientado AB é um segmento em quê admitimos o ponto A como origem e o ponto B como extremidade. O mesmo segmento, orientado no sentido ôpôsto, tem origem em B e extremidade em A e é indicado por BA.
Nas figuras, a seta aponta para as extremidades B e D dos segmentos orientados AB e cê dê. Observe quê os segmentos são paralelos e têm o mesmo comprimento e sentidos opostos.
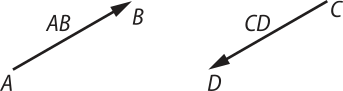
No plano, o vetor , determinado pelo segmento orientado AB, é o conjunto de todos os segmentos orientados quê:
• são paralelos ou colineares ao segmento orientado AB;
• têm o mesmo comprimento (módulo) quê o segmento orientado AB;
• têm o mesmo sentido do segmento orientado AB.

Quando tratamos de vetores, qualquer um dos segmentos orientados do conjunto póde sêr tomado como representante. Note quê qualquer outro segmento orientado na figura anterior é também um representante do vetor .
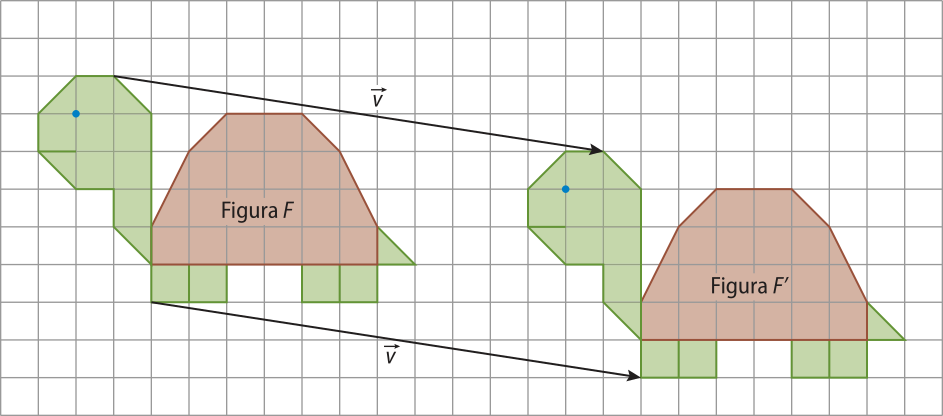
Sendo um vetor do plano (alfa)", a translação pelo vetor é a transformação T quê associa cada ponto P de (alfa)" ao ponto P1, de modo quê PP1 seja um segmento orientado do vetor .
Usamos a notação P1 = P + para indicar a translação do ponto P pelo vetor .
É comum imaginarmos quê o vetor transportou o ponto P para a posição P1. Observe, no exemplo a seguir, como temos a impressão de quê cada ponto da figura F foi deslocado pelo vetor para sua nova posição, formando a figura F(minutos)".
Página duzentos e sessenta e três
Rotação
No plano, o ângulo orientado é um ângulo em quê admitimos a semirreta como origem e a semirreta como extremidade. O mesmo ângulo, orientado no sentido ôpôsto, tem origem em e extremidade em e é indicado por .
Nas figuras, a seta aponta para as semirretas quê são as extremidades dos ângulos orientados e . Observe quê esses ângulos têm sentidos opostos. Para simplificar a comunicação, vamos dizêr quê o ângulo é medido no sentido horário, enquanto o ângulo é medido no sentido anti-horário.
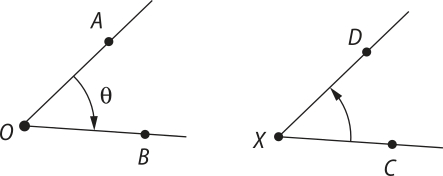
Sendo A um ponto do plano (alfa)" e θ = um ângulo orientado, a rotação de centro em A e ângulo θ é a transformação T quê associa cada ponto P de (alfa)" ao ponto P1, de modo quê:
• os segmentos de reta e tênham o mesmo comprimento, ou seja, AP = AP1;
• a medida do ângulo seja igual à medida do ângulo θ, ou seja, m () = θ;
• o ângulo orientado tenha o mesmo sentido quê o ângulo orientado .
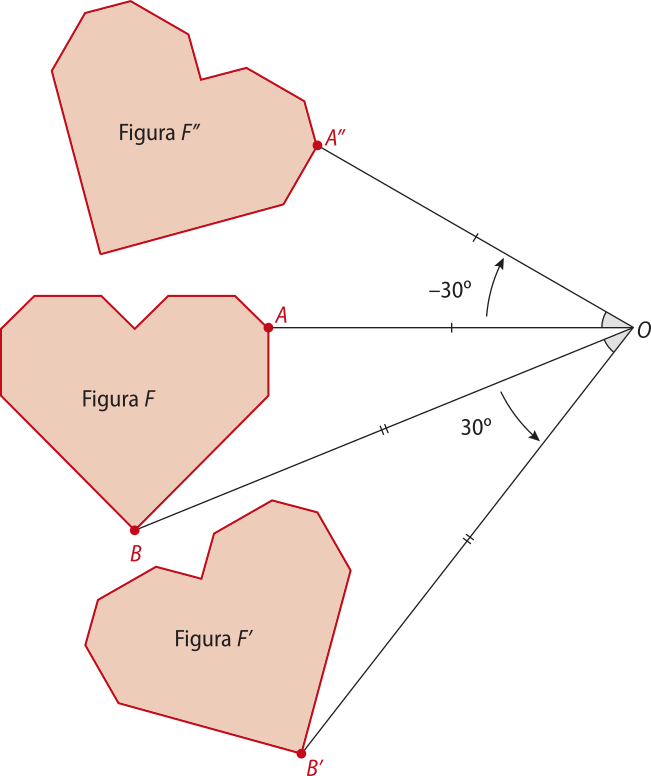
Convencionamos quê a rotação se dará no sentido anti-horário para valores de θ positivos e no sentido horário para valores de θ negativos. Por exemplo, a figura F(minutos)" é imagem da figura F por uma rotação de um ângulo de medida 30° em torno do ponto O, enquanto a figura F(segundos)" é imagem da figura F por uma rotação de um ângulo de medida −30° em torno do ponto O.
Note quê OB = OB(minutos)" e (sentido anti-horário de rotação) e quê OA = OA(segundos)" e (sentido horário de rotação).
Como alternativa à utilização do sinal da medida do ângulo para indicar o sentido de rotação, pode-se deixar o sentido explícito no texto, por exemplo: a figura F(minutos)" é imagem da figura F por uma rotação de um ângulo de medida 30° no sentido anti-horário em torno do ponto O, enquanto a figura F(segundos)" é imagem da figura F por uma rotação de um ângulo de medida 30° no sentido horário em torno do ponto O.
Página duzentos e sessenta e quatro
É importante destacar quê a rotação de ângulo 180° em torno de um ponto O coincide com a reflekção dessa figura em relação ao ponto O. Observe um exemplo díssu na figura a seguir.
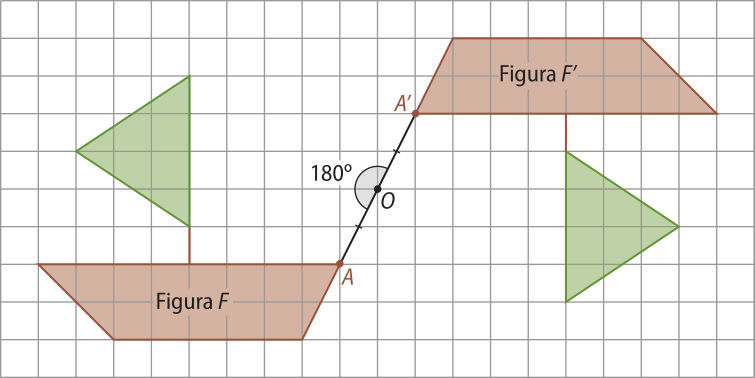
FÓRUM
Confecções indígenas
Os artefatos das comunidades indígenas trazem consigo, além de apelo visual, informações culturais relacionadas a saberes transmitidos de geração para geração.
Nas imagens a seguir, temos exemplos de grafismos indígenas na ár-te da cestaria de arumã, uma planta nativa da Amazônea, feita pelo povo baniwa, do Alto Xingu.

Ver as Orientações para o professor.
![]() Converse com os côlégas e o professor sobre as kestões a seguir.
Converse com os côlégas e o professor sobre as kestões a seguir.
• Vocês já conheciam esse tipo de grafismo? Os grafismos das imagens apresentam algum tipo de isometria?
Resposta pessoal. Espera-se quê os estudantes identifiquem reflekções, translações e rotações nas fotografias dos balaios.
• Pesquisem sobre a; ár-te dos povos indígenas do Brasil e da sua região. Selecionem alguns grafismos pesquisados, apresentem as imagens aos côlégas e discutam a importânssia da valorização da ár-te indígena.
Pesquisa dos estudantes. Espera-se quê os estudantes compreendam quê as diferentes culturas devem sêr respeitadas e valorizadas em sua diversidade.
Página duzentos e sessenta e cinco
ATIVIDADES RESOLVIDAS
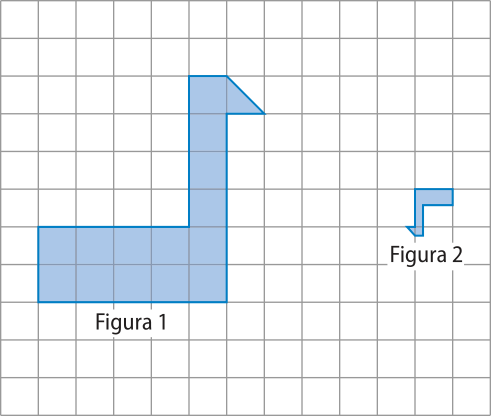
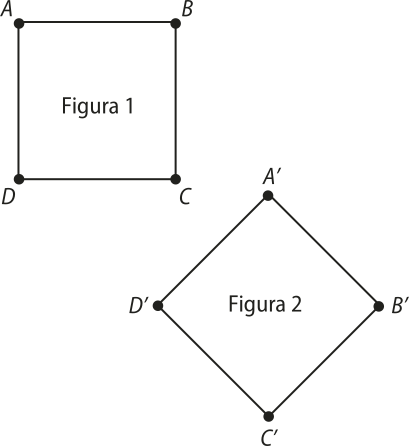
1. Observe as figuras congruentes na malha quadriculada, em quê o lado de cada quadrado méde 1 u.c., e verifique se a figura 2 é a reflekção da figura 1 em relação à reta r. Justifique.
a) 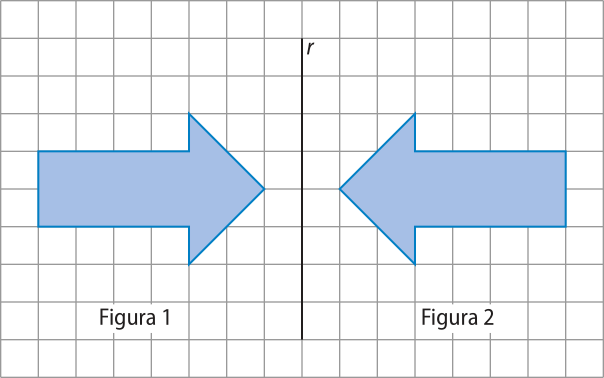
b)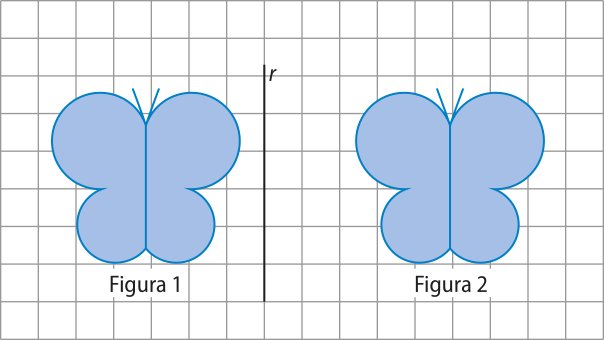
Resolução
a) Observe, na malha quadriculada, quê a reta r é a mediatriz dos segmentos determinados por qualquer ponto da figura 1 e o ponto correspondente da figura 2. Logo, a figura 2 é a reflekção da figura 1 em relação à reta r.
b) Pela malha quadriculada, temos quê a reta r não é a mediatriz de qualquer segmento de reta determinado por um ponto da figura 1 e o ponto correspondente da figura 2. Portanto, a figura 2 não é a reflekção da figura 1 em relação à reta r.
2. Quais são as isometrias das figuras F1, F2, F3 e F4 em relação à figura F na malha quadriculada a seguir? Considere a medida do lado do quadrado da malha igual a 1 u.c.
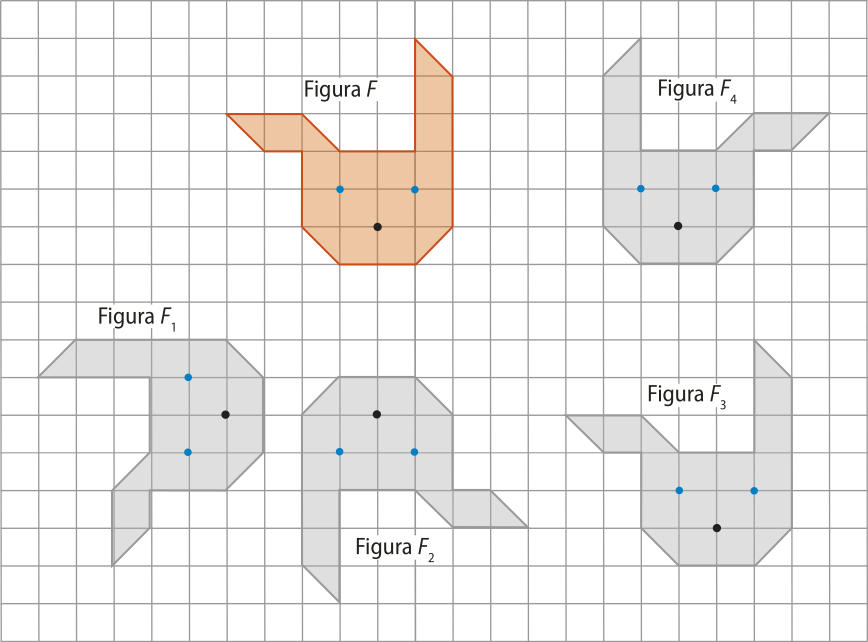
Página duzentos e sessenta e seis
Resolução
Vamos analisar caso a caso.
• A figura F1 é a rotação de 90° de F em torno do ponto P no sentido anti-horário.
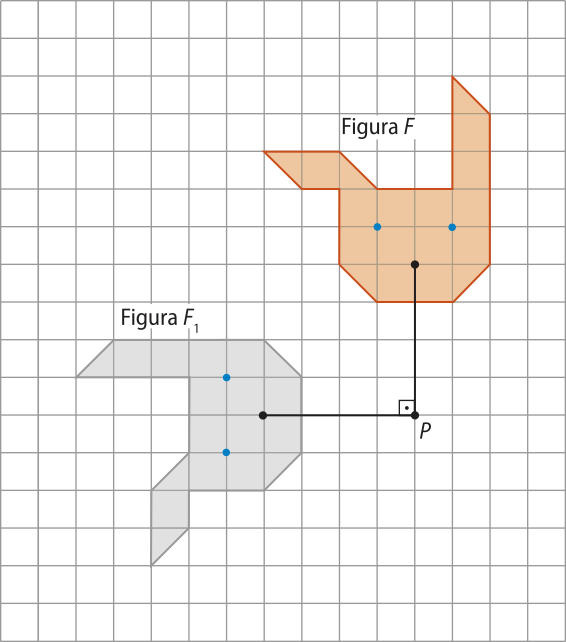
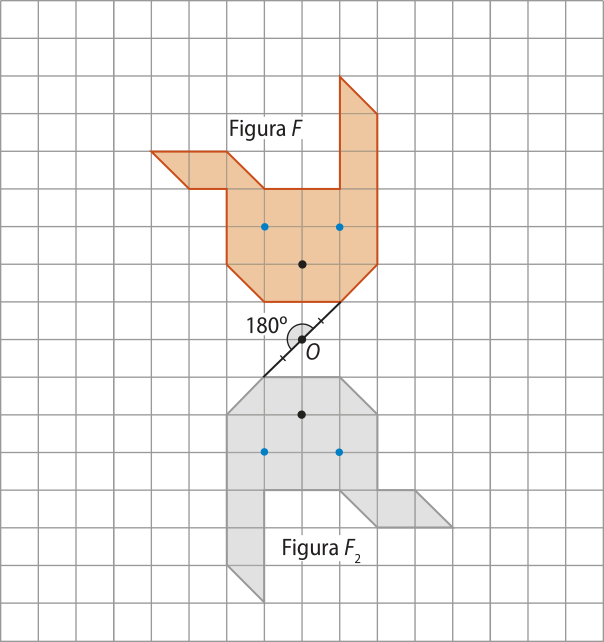
• A figura F2 é a reflekção de F em relação ao ponto O e é também a rotação de 180° de F em torno do ponto O.
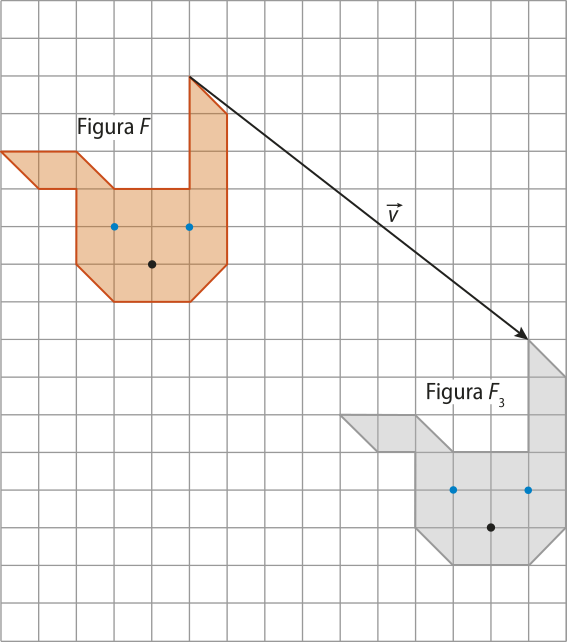
• A figura F3 é a translação de F pelo vetor .
• A figura F4 é a reflekção de F em relação à reta r.

Página duzentos e sessenta e sete
3. Em algumas culturas, as mandalas simbolizam harmonía e equilíbrio e, por esse motivo, são freqüentemente utilizadas na Arquitetura e em decorações. Observe a seguir a ilustração de uma mandala.

Note quê parte do desenho quê compõe a mandala se repete de acôr-do com um padrão. O elemento destacado no zoom, por exemplo, repete-se outras sete vezes.
a) Como é chamada a transformação quê podemos associar às repetições do elemento destacado da mandala?
b) dêz-creva a rotação quê associa o elemento I ao elemento II destacado considerando o sentido horário. Agora, dêz-creva a rotação considerando o sentido anti-horário.
Resolução
a) Rotação em torno de um ponto (centro da mandala).
b) Como há 8 repetições, o menor ângulo de rotação é obtído pela divisão da volta completa (360°) por 8, ou seja, = 45°. Assim, o elemento II é a rotação de −45° (sentido horário) do elemento I em torno do centro da mandala. Caso seja considerada a rotação em torno do centro da mandala no sentido anti-horário, o ângulo de rotação será 360° − 45° = 315°.
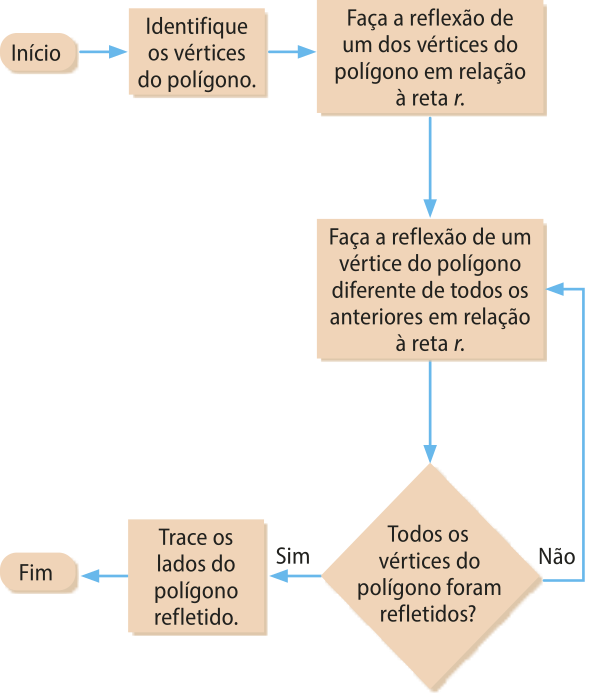
4. Construa um fluxograma quê indique os passos para desenhar a reflekção em relação à reta r do polígono mostrado a seguir.

Resolução
Para desenhar a reflekção de um polígono em relação a uma reta, determinamos primeiro as imagens dos vértices; em seguida, traçamos os lados do polígono. O fluxograma a seguir indica os passos necessários para essa construção.
Pense e responda
• Faz diferença o vértice escolhido para começar o processo? Explique.
Não, pois cada reflekção é independente das outras.
• Esse processo sérve para refletir qualquer polígono em relação a uma reta? Explique.
Sim, pois, no fluxograma, não foram utilizadas características específicas de nenhum polígono, apenas elementos gerais.
Página duzentos e sessenta e oito
ATIVIDADES
1. Determine em quais das imagens a seguir podemos admitir simetria em relação a uma reta. As imagens não estão em proporção.
a) 
b) 
c) 
Nas imagens dos itens a e b.
2. Observe as figuras na malha quadriculada a seguir, em quê a medida do lado de cada quadrado méde 1 u.c., e responda às perguntas.
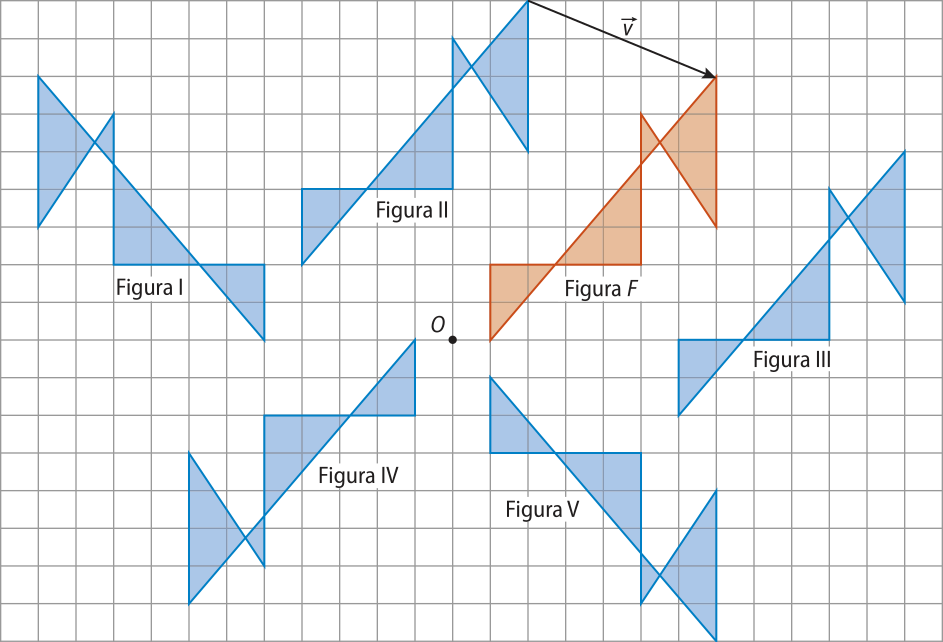
a) Qual figura representa a reflekção da figura F em relação a uma reta vertical?
figura I
b) Qual figura representa a translação da figura F pelo vetor ?
figura III
c) Qual figura representa a rotação da figura F em 180° em torno do ponto O?
figura IV
3. Desenhe, em uma fô-lha de papel quadriculado, o polígono P’, quê é a reflekção do polígono P a seguir em relação à reta r.
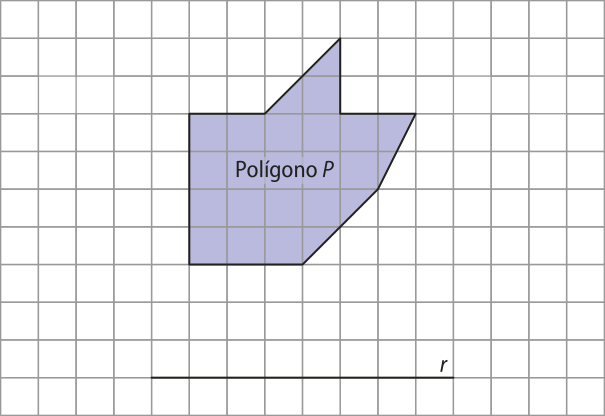
Ver as Orientações para o professor.
Página duzentos e sessenta e nove
4. (Enem/MEC) Um programa de edição de imagens possibilita transformar figuras em ou
tras mais compléksas. Deseja-se construir uma nova figura a partir da original. A nova figura deve apresentar simetria em relação ao ponto O.

A imagem quê representa a nova figura é:
a) 
b) 
c) 
d) 
e) 
alternativa e
5. Observe a figura a seguir, quê representa uma pipa em uma malha quadriculada.
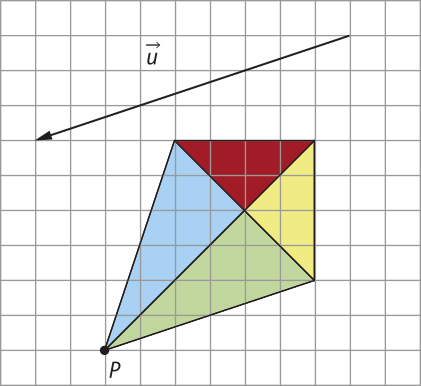
Agora, desenhe, em uma fô-lha de papel quadriculado, as figuras obtidas a partir de cada uma das transformações a seguir.
a) Translação pelo vetor .
Ver as Orientações para o professor.
b) Rotação de 180° em torno do ponto P no sentido anti-horário.
Ver as Orientações para o professor.
• Como ficaria a figura rotacionada, se, no item b, mantendo o ângulo e o centro de rotação, fizéssemos a rotação em sentido horário?
A figura ficaria igual.
6. (Enem/MEC) A imagem apresentada na figura é uma cópia em preto e branco da tela quadrada intitulada O peixe, de Marcos Pinto, quê foi colocada em uma parede para exposição e fixada nos pontos A e B. Por um problema na fixação de um dos pontos, a tela se desprendeu, girando rente à parede. Após o giro, ela ficou posicionada como ilustrado na figura, formando um ângulo de 45° com a linha do horizonte.
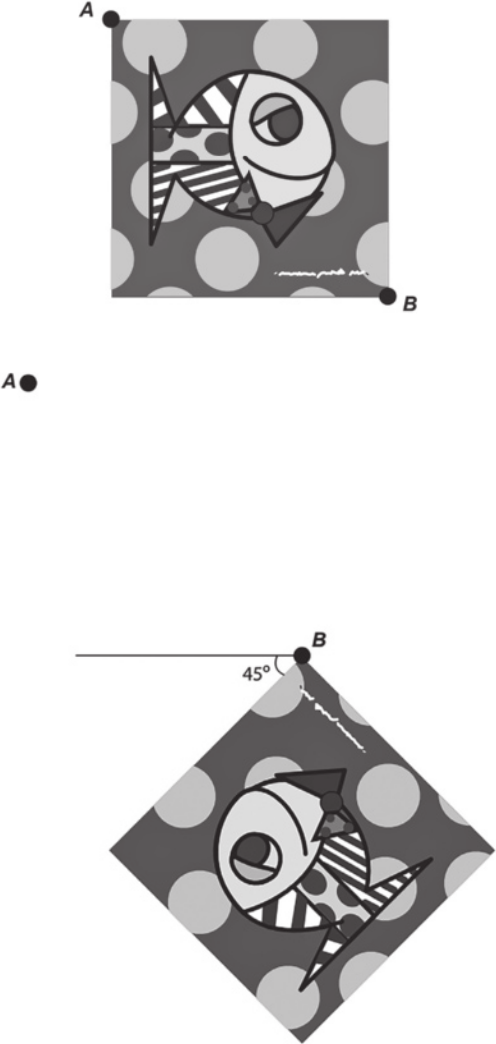
Página duzentos e setenta
Para recolocar a tela na sua posição original, deve-se girá-la, rente à parede, no menor ângulo possível inferior a 360°. A forma de recolocar a tela na posição original, obedecendo ao quê foi estabelecido, é girando-a em um ângulo de
a) 90° no sentido horário.
b) 135° no sentido horário.
c) 180° no sentido anti-horário.
d) 270° no sentido anti-horário.
e) 315° no sentido horário.
alternativa b
7. (Enem/MEC) As figuras a seguir exibem um trecho de um quêbra-cabeças que está sêndo montado.
Observe quê as peças são quadradas e há 8 peças no tabuleiro da figura A e 8 peças no tabuleiro da figura B. As peças são retiradas do tabuleiro da figura B e colocadas no tabuleiro da figura A na posição correta, isto é, de modo a completar os dêzê-nhôs.
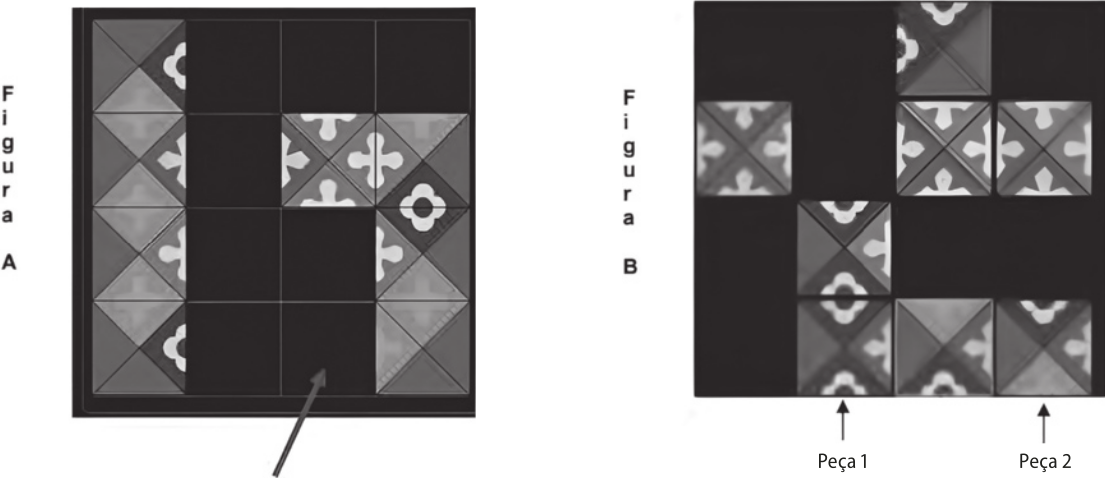
Disponível em: ht tp://pt.eternityii.com. Acesso em: 14 jul. 2009.
É possível preencher corretamente o espaço indicado pela seta no tabuleiro da figura A colocando a peça
a) 1 após girá-la 90° no sentido horário.
b) 1 após girá-la 180° no sentido anti-horário.
c) 2 após girá-la 90° no sentido anti-horário.
d) 2 após girá-la 180° no sentido horário.
e) 2 após girá-la 270° no sentido anti-horário.
alternativa c
8. (Cefet-MG) As cartas de um baralho tradicional possuem características para facilitar a visualização dos jogadores. A ideia é de quê elas possam sêr lidas de “cabeça para baixo”, isto é, não é necessário rotacionar uma carta em 180° para quê ela possa sêr compreendida. De fato, algumas cartas são idênticas se vistas em posições distintas, por meio de uma rotação. Considere a figura a seguir composta por cinco cartas:

O número de cartas dessa figura quê exibirão exatamente a mesma imagem após uma rotação de 180° é
a) 1
b) 2
c) 3
d) 4
alternativa c
Página duzentos e setenta e um
Composição de transformações
Na imagem a seguir, podemos observar duas figuras congruentes, F1 e F2, quê não são imagens uma da outra por nenhuma das isometrias estudadas até o momento.
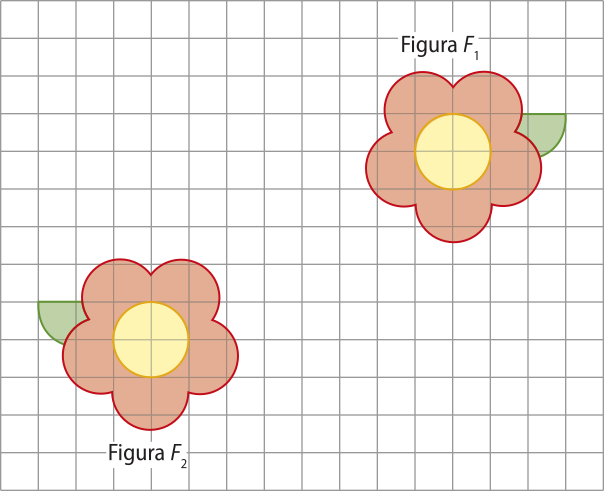
No entanto, se considerarmos uma figura auxiliar F(minutos)", conseguimos identificar algumas isometrias. Acompanhe:
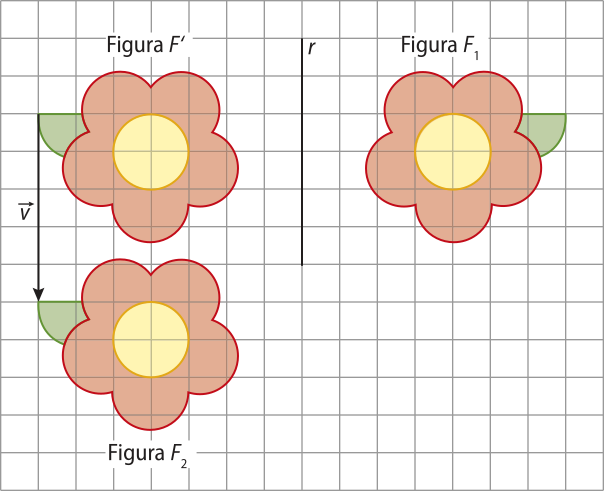
• A figura F(minutos)" é a reflekção em relação à reta r da figura F1.
• A figura F2 é a translação pelo vetor da figura F(minutos)".
Assim, dizemos quê a figura F2 é imagem da figura F1 por meio de uma composição de transformações.
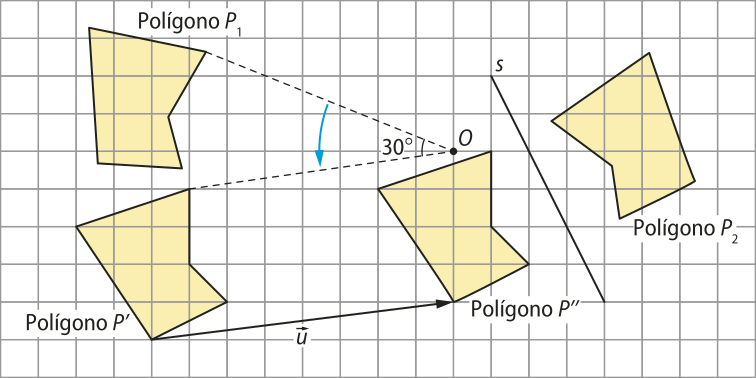
Acompanhe outro exemplo. O polígono P2 póde sêr associado ao polígono P1 pela seguinte composição:
• O polígono P(minutos)" é a rotação de 30° em torno do ponto O no sentido anti-horário de P1.
• O polígono P(segundos)" é a translação pelo vetor de P(minutos)".
• O polígono P2 é a reflekção em relação à reta s de P(segundos)".
Página duzentos e setenta e dois
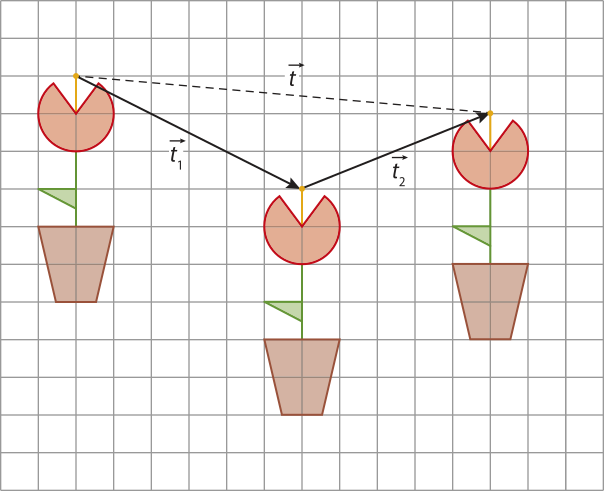
Um caso de composição de transformações interessante de sêr analisado é a composição de duas translações, quê sempre resulta em uma nova translação. Observe um exemplo a seguir.
A translação pelo vetor é a composição da translação pelo vetor seguida da translação pelo vetor .
ATIVIDADE RESOLVIDA
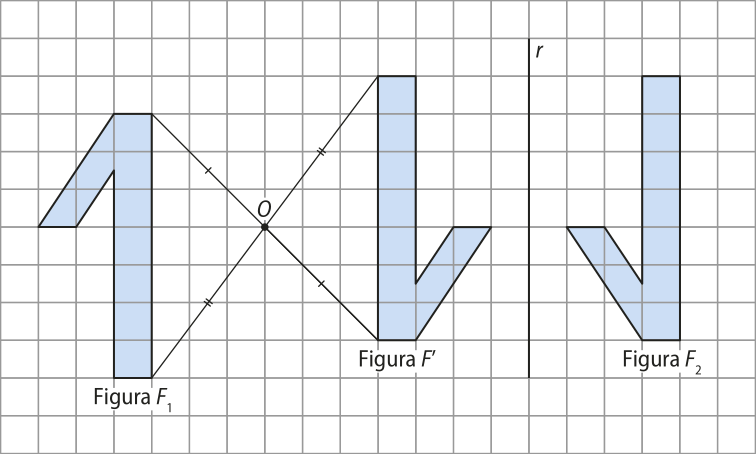
5. Analise as figuras a seguir e identifique isometrias quê, quando compostas, associam as figuras F1 e F2.

Resolução
Uma composição possível é uma reflekção em relação a um ponto seguida de uma reflekção em relação a uma reta. Para isso, considere a figura F(minutos)", quê é a reflekção em relação ao ponto O da figura F1. Por fim, a figura F2 é a reflekção em relação à reta r da figura F(minutos)".
Página duzentos e setenta e três
ATIVIDADES
9. Copie a figura a seguir em uma fô-lha de papel quadriculado e faça o quê se pede.
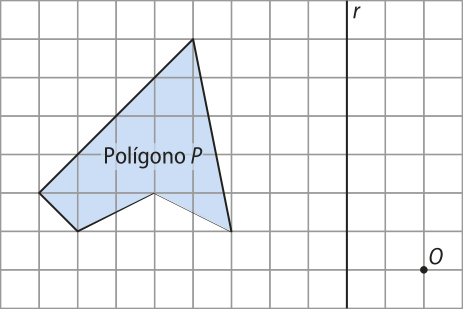
a) Desenhe a imagem Pa do polígono P dada pela seguinte composição:
• P1 é a reflekção em relação ao ponto O do polígono P;
• Pa é a reflekção em relação à reta r de P1.
b) Obtenha a imagem Pb do polígono P dada pela seguinte composição:
• P2 é a reflekção em relação à reta r de P;
• Pb é a reflekção em relação ao ponto O de P2.
Ver as Orientações para o professor.
10. Copie a figura F a seguir em uma fô-lha de papel quadriculado e desenhe as figuras indicadas.
a) F1, quê é a rotação de 90° no sentido horário em torno do ponto O da figura F;
b) F2, quê é a rotação de 90° no sentido horário em torno do ponto O da figura F1;
c) F3, quê é a rotação de 90° no sentido horário em torno do ponto O da figura F2.
Para finalizar, pinte as imagens obtidas após cada rotação com cores diferentes.
Ver as Orientações para o professor.
11. Analise os polígonos congruentes a seguir e identifique isometrias quê, quando compostas, associam o polígono P1 ao polígono P2.
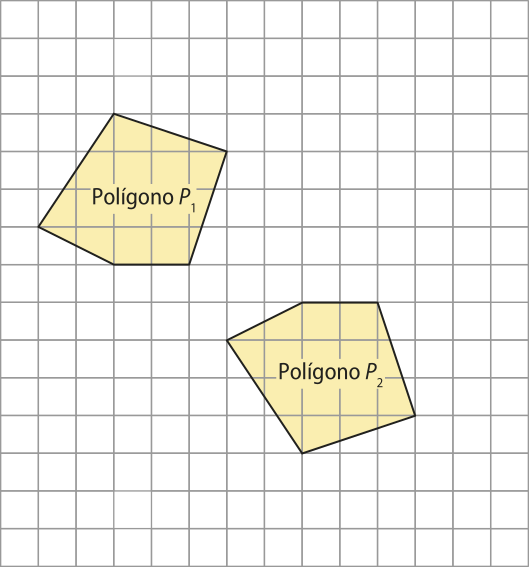
Ver as Orientações para o professor.
12. (Cefet-MG). A figura representada na malha quadriculada foi disponibilizada em uma aula de Matemática juntamente com a indicação das transformações 1, 2 e 3. O professor indicou quê essas transformações deveriam sêr realizadas, nessa ordem, em tal figura.
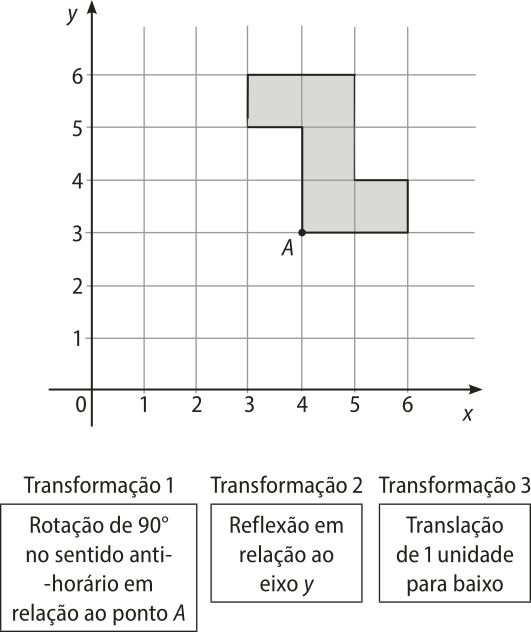
Página duzentos e setenta e quatro
Após a realização dessas três transformações, a figura resultante está representada em
a) 
b) 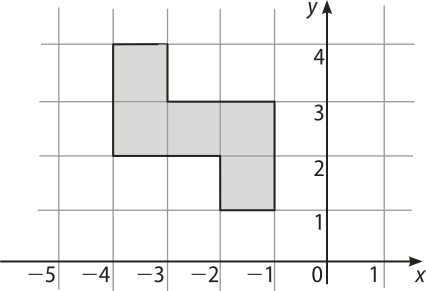
c) 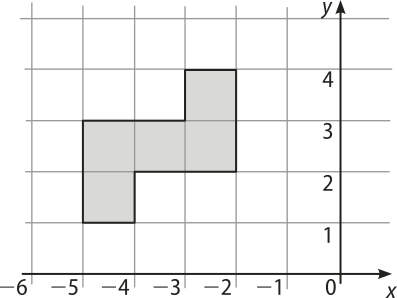
d) 
alternativa b
13. Assinale a alternativa quê apresenta a imagem Pi do polígono P dada pela composição das transformações a seguir.
• 1ª transformação: P(minutos)" é a rotação de 90° em torno do ponto O no sentido horário do polígono P;
• 2ª transformação: Pi é a reflekção em relação à reta r do polígono P(minutos)".
a) 
b) 
c) 
d) 
alternativa d
Página duzentos e setenta e cinco
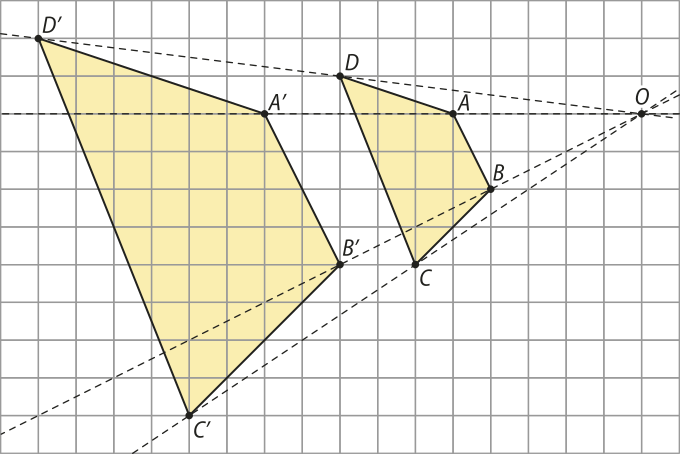
Transformações homotéticas
Na introdução do Capítulo, analisamos uma obra de é-chêr quê apresentava figuras idênticas em diferentes posições. Agora, vamos observar outra de suas obras.
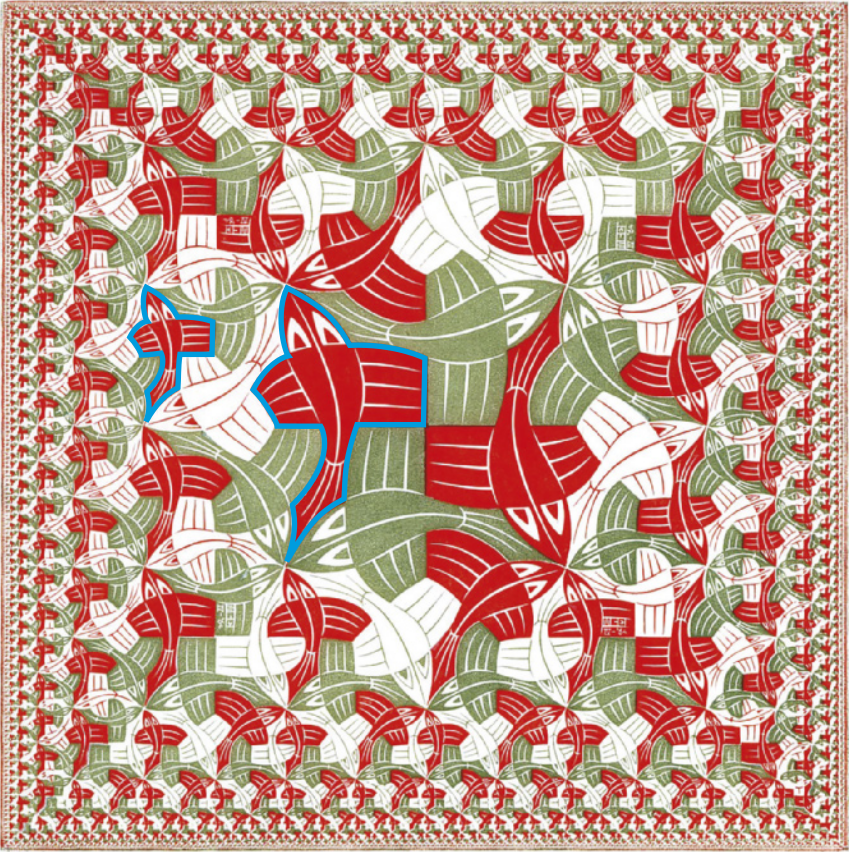
Considere os dois peixes destacados em azul. Eles ilustram a noção intuitiva de duas figuras planas semelhantes. Em Matemática, dois polígonos são semelhantes quando os ângulos correspondentes são congruentes e os lados correspondentes são proporcionais, por exemplo, dois quadrados são sempre semelhantes entre si.
Estudaremos, neste tópico, a associação entre dois polígonos semelhantes por meio de uma transformação geométrica denominada homotetia.
Sendo O um ponto do plano (alfa)" e k um número real, em quê k ≠ 0, a homotetia de centro em O e de razão k é a transformação T quê associa cada ponto P de (alfa)" ao ponto P1, de modo quê os pontos O, P e P1 sêjam colineares e quê:
,
em quê:
• é o vetor determinado pelo segmento orientado ;e
• é o vetor determinado pelo segmento orientado OP.
Os pontos P e P1 são chamados de homólogos.
Página duzentos e setenta e seis
Conforme o valor da razão k, classificamos as homotetias em:
• diréta, quando k > 0;
• invérsa, quando k < 0.
Classificamos também a homotetia em:
• ampliação, quando |k| > 1;
• redução, quando 0 < |k| < 1.
Na malha quadriculada a seguir, em quê o lado de cada quadrado méde 1 u.c., o polígono F(minutos)" é a redução do polígono F por uma homotetia diréta de centro O e razão k = .
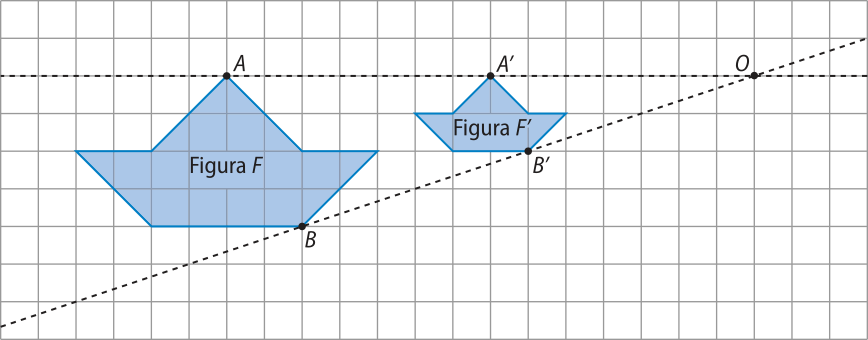
Observe no exemplo quê:
• os pontos A e A(minutos)", bem como os pontos B e B(minutos)", são homólogos.
• o centro O, intersecção das retas e , não pertence ao segmento nem ao segmento . Isso ocorre quando a homotetia é diréta.
• a razão de homotetia k é positiva e póde sêr determinada por:
d(O, A(minutos)") = k ⋅ d(O, A) ⇒ k =
• a razão de semelhança entre os polígonos F(minutos)" e F é igual à razão de homotetia.
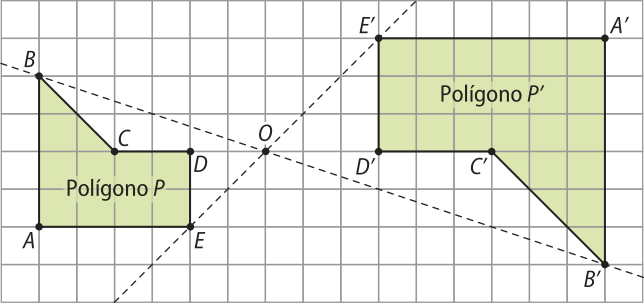
O exemplo a seguir ilustra, em uma malha quadriculada, na qual o lado de cada quadrado méde 1 u.c., o polígono P(minutos)", quê é uma ampliação do polígono P por uma homotetia invérsa de centro O e razão k = .
Página duzentos e setenta e sete
Observe no exemplo quê:
• o centro O, intersecção das retas e pertence ao segmento e pertence também ao segmento . Isso ocorre quando a homotetia é invérsa.
• a razão de homotetia k é negativa e póde sêr determinada por:
• uma homotetia invérsa de razão igual a −1 seria igual a uma reflekção em relação a um ponto.
Para construir a ampliação diréta de um polígono por uma homotetia, primeiro, determinamos as imagens de seus vértices e, depois, traçamos os lados. Acompanhe o passo a passo.
1. Dados o quadrilátero ABCD, o centro O da homotetia e sua razão k = 2, traçamos as retas quê passam por O e por cada um dos vértices do quadrilátero.

2. Como k > 0, trata-se de uma homotetia diréta, portanto os vértices A(minutos)", B(minutos)", C(minutos)" e D(minutos)" do polígono ampliado devem estar nas semirretas , , e respectivamente, de modo quê OA(minutos)" = 2 ⋅ OA, OB(minutos)" = 2 ⋅ OB, OC(minutos)" = 2 ⋅ OC e OD(minutos)" = 2 ⋅ OD. Para se obterem as medidas OA(minutos)", OB(minutos)", OC(minutos)" e OD(minutos)", os comprimentos OA, OB, OC e OD devem sêr medidos com régua graduada diretamente na figura e substituídos nas equações indicadas anteriormente. A partir díssu, obtemos os vértices da nova figura.
3. Com a régua, traçam-se os segmentos , , e , lados do quadrilátero A(minutos)"B(minutos)"C(minutos)"D(minutos)", imagem do quadrilátero ABCD pela homotetia considerada.
Página duzentos e setenta e oito
ATIVIDADE RESOLVIDA
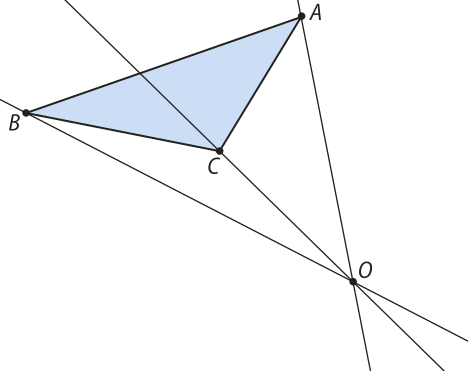
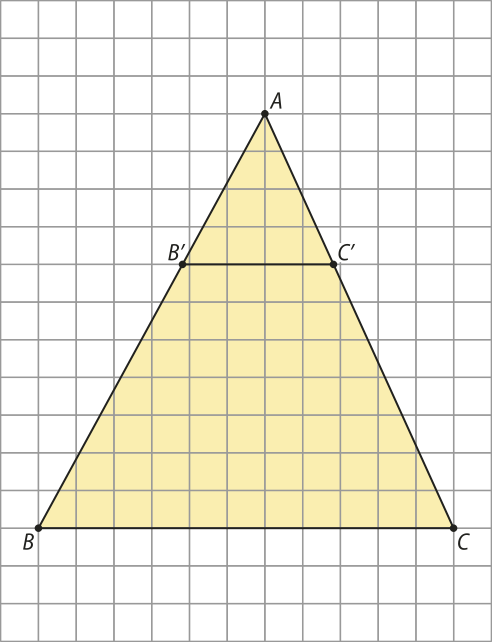
6. Construa a imagem A(minutos)"B(minutos)"C(minutos)" do triângulo ABC por uma homotetia invérsa de centro O, de modo quê a área do triângulo A(minutos)"B(minutos)"C(minutos)" seja da área do triângulo ABC.

Resolução
Sendo SABC e SA(minutos)"B(minutos)"C(minutos)", respectivamente, as áreas dos triângulos ABC e A(minutos)"B(minutos)"C(minutos)", pelo enunciado, temos quê:
SA(minutos)"B(minutos)"C(minutos)" = ⋅ SABC ⇒ SABC = 9 ⋅ SA(minutos)"B(minutos)"C(minutos)"
A razão de homotetia k é a razão de semelhança entre os triângulos A(minutos)"B(minutos)"C(minutos)" e ABC. Desse modo, a razão de homotetia elevada ao quadrado é igual à razão entre as áreas dos triângulos A(minutos)"B(minutos)"C(minutos)" e ABC, ou seja:
Como se trata de uma homotetia invérsa, temos quê k < 0. Logo, k = .
Agora, podemos seguir o passo a passo:
1. Traçamos as retas , e .
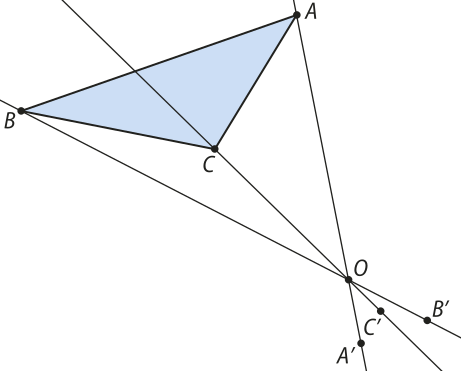
2. Como se trata de uma homotetia invérsa, os vértices A(minutos)", B(minutos)" e C(minutos)" devem estar nas semirretas opostas a , e respectivamente, de modo quê , OB(minutos)" = e , lembrando quê os comprimentos OA, OB e OC são medidos com régua graduada diretamente na figura. Dessa maneira, obtemos os vértices da homotetia.
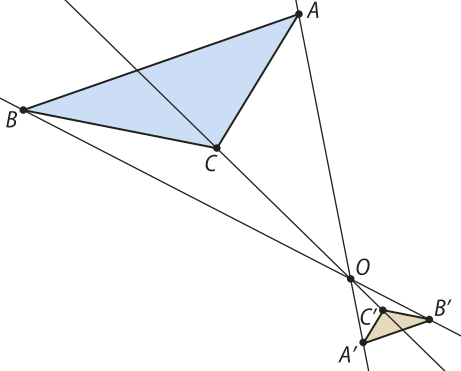
3. Com a régua, traçam-se os segmentos , e lados do triângulo A(minutos)"B(minutos)"C(minutos)", imagem do triângulo ABC pela homotetia considerada.
Página duzentos e setenta e nove
ATIVIDADES
14. Sabendo quê a figura 2 é a imagem da figura 1 por uma homotetia, faça o quê se pede.
a) Classifique a homotetia em diréta ou invérsa.
homotetia invérsa
b) Calcule a razão de homotetia. Para isso, considere a medida do lado dos quadrados da malha quadriculada igual a 1 u.c.
−0,2
15. Na figura a seguir, o triângulo AB(minutos)"C(minutos)" é a imagem do triângulo ABC por uma homotetia.
Determine:
a) o centro da homotetia;
ponto A
b) a razão da homotetia.
16. Copie a figura a seguir em uma fô-lha de papel quadriculado e desenhe a imagem do quadrilátero ABCD pela homotetia de centro C e razão .

Ver as Orientações para o professor.
17. A área de um triângulo ABC é 8 vezes a área de um triângulo A(minutos)"B(minutos)"C(minutos)". Qual é a razão da homotetia diréta entre o triângulo maior e o triângulo menor?
18. As figuras 1 e 2 são imagens por homotetias da figura F. Para cada uma delas, determine a classificação da homotetia e sua razão. Considere a medida do lado dos quadrados da malha quadriculada como 1 u.c.
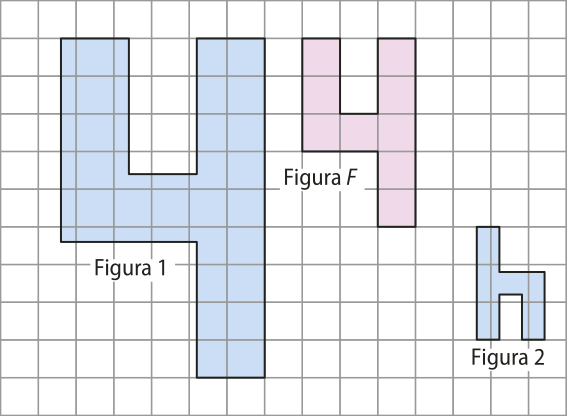
Figura 1: ampliação diréta; a razão de homotetia é 1,8.
Figura 2: redução invérsa; a razão de homotetia é −0,6.
• A figura 2 é imagem da figura 1 por homotetia? Se sim, qual é a razão dessa homotetia?
sim,
Página duzentos e oitenta
Transformações geométricas e matrizes
Acompanhe, neste tópico, o estudo das transformações geométricas por meio de matrizes.
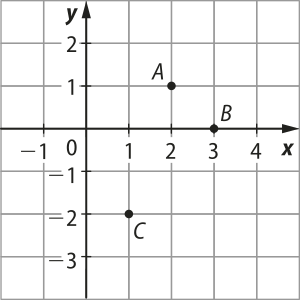
Um ponto P(x, y) do plano cartesiano póde sêr representado pela matriz coluna . Por exemplo, os pontos A(2, 1), B(3, 0) e C(1, −2), representados no plano cartesiano a seguir, em notação matricial, são expressos por:
• • •
Os vértices A(2, 1), B(3, 0) e C(1, −2) de um triângulo, no plano cartesiano, podem sêr representados pela seguinte notação matricial:
, ou seja .
Reflexão em relação aos eixos coordenados
Em um plano cartesiano, a reflekção em relação ao eixo x associa um ponto (a, b) do plano ao ponto (a, −b). Essa associação póde sêr ôbitída por meio da multiplicação matricial:
,
em quê é denominada matriz de reflekção em relação ao eixo x.
A reflekção em relação ao eixo y associa um ponto (a, b) do plano ao ponto (−a, b), associação quê póde sêr ôbitída pela multiplicação matricial:
,
em quê é denominada matriz de reflekção em relação ao eixo y.
Exemplo:
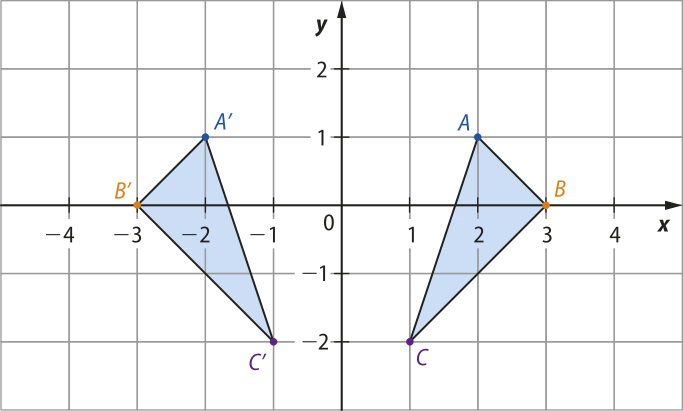
Os vértices de um triângulo em um plano cartesiano são A(2, 1), B(3, 0) e C(1, −2). As coordenadas dos vértices do triângulo A(minutos)"B(minutos)"C(minutos)", reflekção do triângulo ABC em relação ao eixo y, são dadas pela multiplicação entre a matriz de reflekção em relação ao eixo y e a matriz quê contém as coordenadas dos vértices do triângulo ABC, isto é:
Página duzentos e oitenta e um
Substituindo os valores das coordenadas e efetuando a multiplicação, temos:
Portanto, as coordenadas dos vértices do triângulo A(minutos)"B(minutos)"C(minutos)" são A(minutos)"(−2, 1), B(minutos)"(−3, 0) e C(minutos)"(−1, −2). Observe a ilustração dessa reflekção no plano cartesiano.
Pense e responda
Quantas linhas e quantas colunas terá uma matriz quê representa um hekzágono?
duas linhas e seis colunas
Translação
Para representar um vetor em notação matricial, utilizamos como representante de o segmento orientado cuja origem coincide com a origem do sistema cartesiano, e sua extremidade (x, y) é indicada pela matriz coluna , ou seja: .
Por exemplo, entre os segmentos orientados de dispostos no plano cartesiano a seguir, consideramos o destacado em vermelho e, assim, denotamos o vetor por .

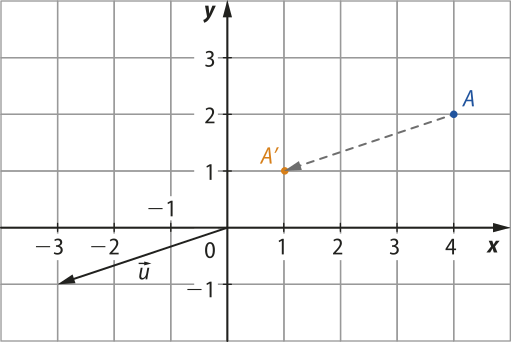
Para determinar as coordenadas (x(minutos)", y(minutos)") da imagem P(minutos)", em quê P(minutos)" é a translação do ponto P(x, y) pelo vetor , em um plano cartesiano, efetuamos a seguinte adição matricial:
Página duzentos e oitenta e dois
Por exemplo, as coordenadas do ponto A(minutos)", translação do ponto A(4, 2) pelo vetor , são (1, 1), pois:
A figura ilustra essa translação.
As coordenadas do vetor de translação seguem um padrão, as translações para a direita têm a coordenada x do vetor positiva e as translações para a esquerda têm a coordenada x do vetor negativa. De modo similar, as translações para cima têm a coordenada y do vetor positiva e as translações para baixo têm a coordenada y do vetor negativa. Desse modo, a translação de 3 unidades para a direita e duas unidades para baixo é expressa pelo vetor .
Quando queremos encontrar as coordenadas de todos os vértices de um polígono P(minutos)", em quê P(minutos)" é a translação pelo vetor do polígono P quê possui n vértices, devemos adicionar a matriz quê contém as coordenadas de P com a matriz quê contém n colunas iguais a .
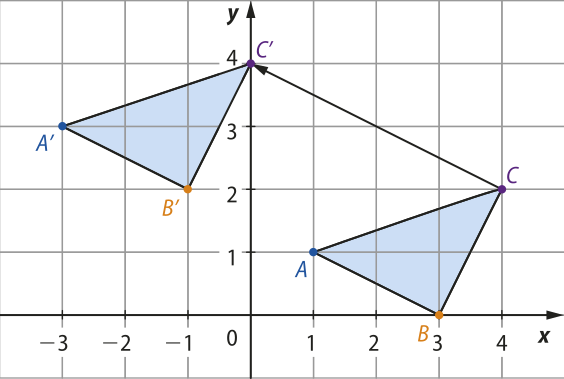
Exemplo:
Os pontos A(1, 1), B(3, 0) e C(4, 2) são vértices de um triângulo. As coordenadas do triângulo A(minutos)"B(minutos)"C(minutos)", translação 4 unidades para a esquerda e duas unidades para cima do triângulo ABC, são obtidas pela adição:
Portanto, os vértices do triângulo A(minutos)"B(minutos)"C(minutos)" são A(minutos)"(−3, 3), B(minutos)"(−1, 2) e C(minutos)"(0, 4).
Página duzentos e oitenta e três
Rotação com centro na origem
Para determinar as coordenadas (x(minutos)", y(minutos)") da imagem P(minutos)", em quê P(minutos)" é a rotação do ponto P(x, y) de um ângulo orientado (alfa)", com (alfa)" > 0, em torno da origem do plano cartesiano, efetuamos a seguinte multiplicação matricial:
Como (alfa)" > 0, o sentido de rotação é anti-horário.
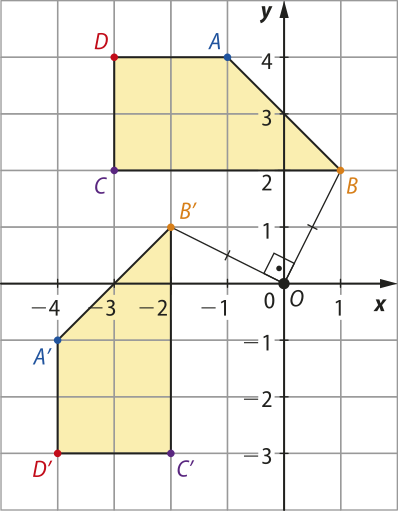
Exemplo:
Considere os pontos A(−1, 4), B(1, 2), C(−3, 2) e D(−3, 4) vértices de um quadrilátero. A rotação com centro na origem do plano cartesiano e ângulo 90° dêêsse quadrilátero resultará em uma imagem cujos vértices são obtidos pela seguinte multiplicação:
Desse modo, temos quê as coordenadas dos vértices da imagem são A(minutos)"(−4, −1), B(minutos)"(−2, 1), C(minutos)"(−2, −3) e D(minutos)"(−4, −3). A figura a seguir ilustra essa rotação.
Quando a medida do ângulo orientado de rotação (alfa)" for negativa, o sentido de rotação é horário. Nesse caso, consideramos quê uma rotação de ângulo (alfa)" no sentido horário equivale a uma rotação de ângulo de medida igual a 360° − (alfa)" no sentido anti-horário. Por exemplo, rotacionar 30° no sentido horário um ponto P em torno da origem do sistema cartesiano equivale a rotacionar o mesmo ponto 330° no sentido anti-horário, pois 360° − 30° = 330°.
Um caso particular de rotação em torno da origem do sistema cartesiano é quando o ângulo (alfa)" é igual a 180°, pois essa rotação coincide com a reflekção em relação à origem do sistema. Nesse caso, para obtêr as coordenadas (x(minutos)", y(minutos)") da imagem P(minutos)", em quê P(minutos)" é a reflekção do ponto P(x, y) em relação à origem, efetuamos a seguinte multiplicação matricial:
Página duzentos e oitenta e quatro
ATIVIDADES RESOLVIDAS
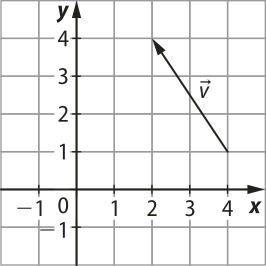
7. Determine as coordenadas da imagem A(minutos)", quê é a translação do ponto A(21, 35) pelo vetor indicado na figura a seguir.
Resolução
O vetor determina a translação duas unidades para a esquerda e 3 unidades para cima, logo = . Como , temos:
Portanto, as coordenadas da imagem são A(minutos)"(19, 38).
8. Considere os pontos A(18, −2), B(3, −5), C(−16, 4) e D(6, 6). A imagem do quadrilátero ABCD após uma reflekção em relação à origem e uma translação de 12 unidades para a direita e 15 unidades para baixo é o quadrilátero A(minutos)"B(minutos)"C(minutos)"D(minutos)". Obtenha as coordenadas dos vértices do quadrilátero A(minutos)"B(minutos)"C(minutos)"D(minutos)".
Resolução
A reflekção em relação à origem coincide com o caso particular de rotação em quê (alfa)" = 180°. Desse modo, para encontrar as coordenadas dos vértices do quadrilátero A(minutos)"B(minutos)"C(minutos)"D(minutos)", fazemos:
Temos, portanto, as seguintes coordenadas: A(minutos)"(−6, −13), B(minutos)"(9, −10), C(minutos)"(28, −19) e D(minutos)"(6, −21).
ATIVIDADES
19. Determine as coordenadas dos vértices da imagem quê resulta de uma reflekção em relação ao eixo y do hekzágono de vértices A(2, 2), B(1, 4), C(−2, 4), D(−3, 0), E(−1, −3) e F(1, −2).
A(minutos)"(−2, 2), B(minutos)"(−1, 4), C(minutos)"(2, 4), D(minutos)"(3, 0), E(minutos)"(1, −3) e F(minutos)"(−1, −2)
20. Assinale a matriz quê representa o vetor de uma translação de 4 unidades para a esquerda.
a)
b)
c)
d)
e)
alternativa c
Página duzentos e oitenta e cinco
21. Considere o vetor representado na figura a seguir.
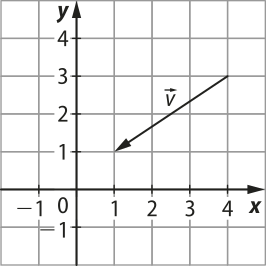
Se P(minutos)"(16, −4) é a imagem do ponto P pela translação pelo vetor , então:
a) P =
b) P =
c) P =
d) P =
e) P =
alternativa c
22. Considere os pontos A, B, C, D, E e F no plano cartesiano e faça o quê se pede.
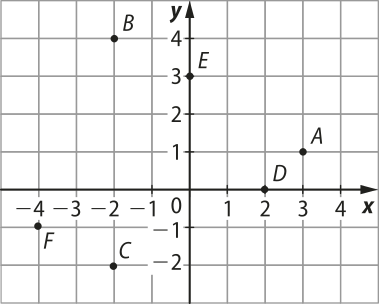
a) escrêeva as coordenadas dos pontos A, B, C, D, E e F em notação matricial.
, , , , e
b) Determine as coordenadas das imagens A1, B1 e C1, sabendo quê elas são, respectivamente, a reflekção em relação ao eixo x dos pontos A, B e C.
A1 (3, −1), B1 (−2, −4) e C1 (−2, 2)
c) Determine as coordenadas dos vértices do triângulo A2B2C2, imagem do triângulo ABC pela translação de vetor .
A2 (4, 4), B2 (−1, 7) e C2 (−1, 1)
d) Determine as coordenadas dos pontos D1, E1 e F1 e das imagens, respectivamente, dos pontos D, E e F por uma reflekção em relação ao eixo y.
D1 (−2, 0), E1 (0, 3) e F1 (4, −1)
e) Determine as coordenadas dos vértices do triângulo D2E2F2, imagem do triângulo DEF por uma rotação de 60° em torno da origem do sistema cartesiano.
23. Considere a matriz . Sabendo quê ela representa todas as coordenadas dos vértices do polígono P, determine:
a) o nome do polígono P.
quadrilátero
b) a matriz quê representa as coordenadas dos vértices da imagem ôbitída pela reflekção em relação ao eixo x do polígono P.
c) a matriz quê representa as coordenadas dos vértices da imagem ôbitída pela translação duas unidades para a direita e 4 unidades para baixo do polígono P.
d) a matriz quê representa as coordenadas dos vértices da imagem ôbitída pela rotação de 90° em torno da origem do sistema cartesiano do polígono P.
24. A equação matricial quê fornece a imagem P(minutos)"(x(minutos)", y(minutos)") de um ponto P(x, y) pela rotação de ângulo (alfa)", com (alfa)" < 0, em torno da origem do sistema cartesiano é:
a)
b)
c)
d)
e)
alternativa b
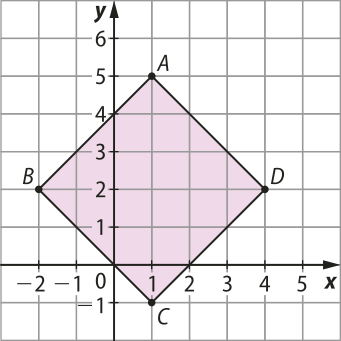
25. Obtenha as coordenadas A(minutos)", B(minutos)", C(minutos)" e D(minutos)" dos vértices da imagem ôbitída pela rotação de 45° em torno da origem do sistema cartesiano do quadrilátero ABCD representado na figura.
Página duzentos e oitenta e seis
CONEXÕES com...
LINGUAGENS E SUAS TECNOLOGIAS
êstér Mahlangu e a cultura ndebele
Os povos africanos são reconhecidos por sua riqueza e diversidade. Nesse contexto, a cultura ndebele surge como uma das expressões mais distintas e fascinantes. De origem situada entre a África do Sul e o Zimbábue, o povo ndebele é conhecido por sua ár-te visual colorida e geométrica. A artista êstér Mahlangu, cujo trabalho apresenta a herança visual dos ndebele, ultrapassou fronteiras e compartilhou a beleza e a profundidade da cultura africana com o mundo. Para saber um pouco mais sobre a artista e a cultura ndebele, leia os textos a seguir.
êstér Mahlangu
Nasceu em 1935, [em] Middelburg, África do Sul.
Vive e trabalha em Mabhoko.
êstér Mahlangu faz parte da comunidade Ndebele em Gauteng, localizada no norte de Pretória. Os Ndebele, ao contrário de muitas outras tribos da África do Sul, conseguiram preservar suas tradições ancestrais centenárias. Apesar de sêr uma ssossiedade patriarcal, o patrimônio artístico é transmitido de mãe para filha; quando uma jovem atinge a puberdade, ela se retira da ssossiedade masculina por três meses e aprende os padrões cerimoniais do bordado Ndebele – no século XIX, essa tradição foi estendida a pinturas decorativas nas paredes, também executadas exclusivamente pelas mulheres Ndebele.
êstér Mahlangu é uma importante defensora dessa tradição. Ela desenha à mão livre, sem medir ou esboçar primeiro, usando tintas vinílicas luminosas e de alto contraste quê conferem um vigor extraordinário aos seus murais. Embora à primeira vista pareçam puramente abstratas, suas composições são construídas com base em um sistema altamente inventivo de signos e símbolos. Mahlangu é a primeira artista Ndebele a transpor pinturas murais para telas e a levar as convenções de sua obra de; ár-te para uma arena mais ampla. Em 1989, ela veio a Paris para criar murais para a exposição Magiciens de la Terre e, ao concordar em realizar outros trabalhos[…], Mahlangu tornou a; ár-te de Ndebele celebrada no mundo inteiro. Ela declarou: “Minha mãe e minha avó me ensinaram a pintar quando eu tinha dez anos. Tenho estado ocupada com isso desde então e sempre gostei. Quando estou pintando meu coração é muito amplo, ele se estende. Isso me faz me sentir muito, muito feliz.”
ESTHER Mahlangu. Genebra: Caacart: The jã Pigozzi African Art collécxion, 2024. Tradução nossa. Disponível em: https://livro.pw/jqwvg. Acesso em: 3 set. 2024.

Página duzentos e oitenta e sete
Casas Ndebele
[…]
Entrelaçar essas cores e seus significados simbólicos através da geometria é uma forma de linguagem para o povo Ndebele. Com suas casas como tela, eles expressam padrões coloridos quê podem comunicar o estátus de um proprietário, o anúncio de um casamento, uma oração ou um protesto. Embora os padrões de cores Ndebele sêjam agora popularizados em todo o mundo e tênham sido aplicados no disáini de produtos como carros e aviões, sua inspiração nos lembra de como a côr na arquitetura póde sêr usada, além de um elemento decorativo, como linguagem.
[…]
YAKUBU, poou. As inspirações por trás das cores da arquitetura tradicional africana. Tradução: Diogo Simões. [S. l.]: ArchDaily, 2 set. 2023. Disponível em: https://livro.pw/oweus. Acesso em: 3 set. 2024.

Agora, faça o quê se pede nas atividades a seguir.
1. Observe a fotografia da fachada da construção ndebele e responda: você consegue identificar padrões quê lembram transformações isométricas? Em caso afirmativo, quais são elas?
Respostas pessoais. Algumas transformações isométricas quê podem sêr citadas são a translação e a reflekção em relação a uma reta.
2. Pesquise uma obra de êstér Mahlangu quê apresente ideias de simetria. Represente em seu caderno a parte da obra quê contém uma dessas ideias.
Resposta pessoal.
3. Tomando como inspiração a obra da artista êstér Mahlangu quê você pesquisou, crie um desenho quê ilustre as ideias das transformações isométricas.
Resposta pessoal.
Página duzentos e oitenta e oito
EXPLORANDO A TECNOLOGIA
Mosaicos no GeoGebra
Vamos utilizar o GeoGebra para criar mosaicos a partir de múltiplas translações de um polígono.
Para isso, realize a sequência de passos a seguir.
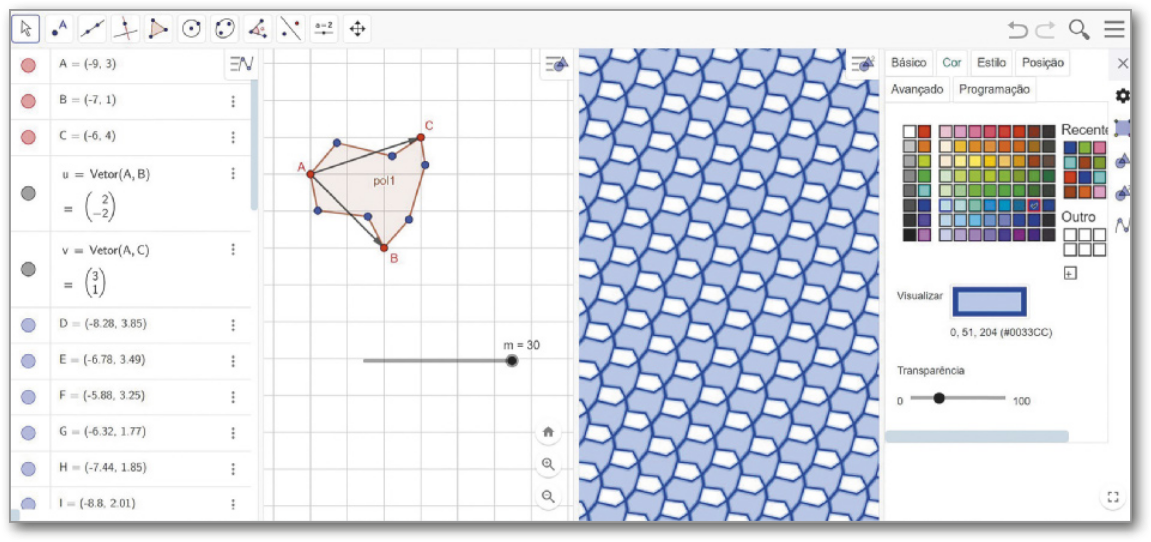
I. Desabilite os eixos e deixe habilitada a malha principal, você póde fazer isso clicando com o botão direito na janela de visualização. Selecione, então, três pontos não colineares na janela de visualização, quê serão nomeados automaticamente como A, B e C. Mude a côr dêêsses três pontos para vermelho, de modo a facilitar a visualização deles. As opções de formatação dos elemêntos estão disponíveis ao clicar sobre o botão ![]() , no canto superior direito da janela de visualização.
, no canto superior direito da janela de visualização.
II. Usando a ferramenta Vetor, ![]() construa um vetor (vetor ) clicando em A e B, nessa ordem, e outro vetor (vetor ) clicando em A e C, nessa ordem.
construa um vetor (vetor ) clicando em A e B, nessa ordem, e outro vetor (vetor ) clicando em A e C, nessa ordem.
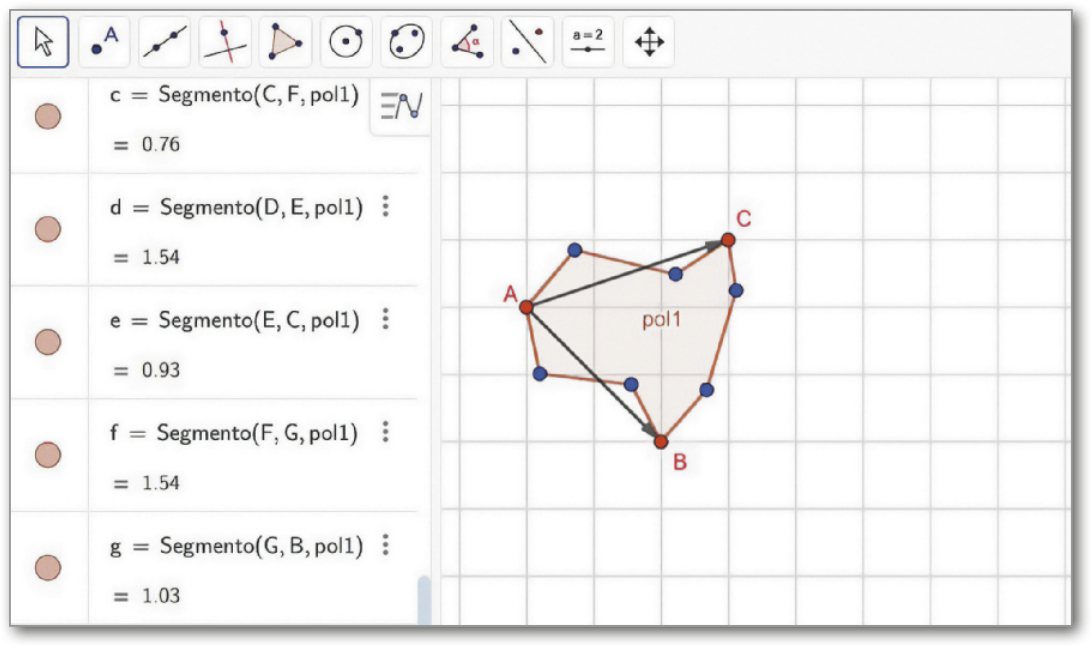
III. Construa pontos entre os pontos A e B, A e C e B e C; para isso, obissérve a figura como exemplo. Depois, usando a ferramenta Polígono, ![]() , construa um polígono quê contenha como vértices os pontos A, B e C e os pontos construídos. Esse polígono será automaticamente nomeado como pol1.
, construa um polígono quê contenha como vértices os pontos A, B e C e os pontos construídos. Esse polígono será automaticamente nomeado como pol1.
IV. Clicando com o botão direito sobre cada elemento e desabilitando a opção Exibir rótulo, oculte os rótulos dos segmentos, dos vetores e dos pontos construídos. Deixe apenas os rótulos dos pontos A, B e C e do polígono pol1.
Página duzentos e oitenta e nove
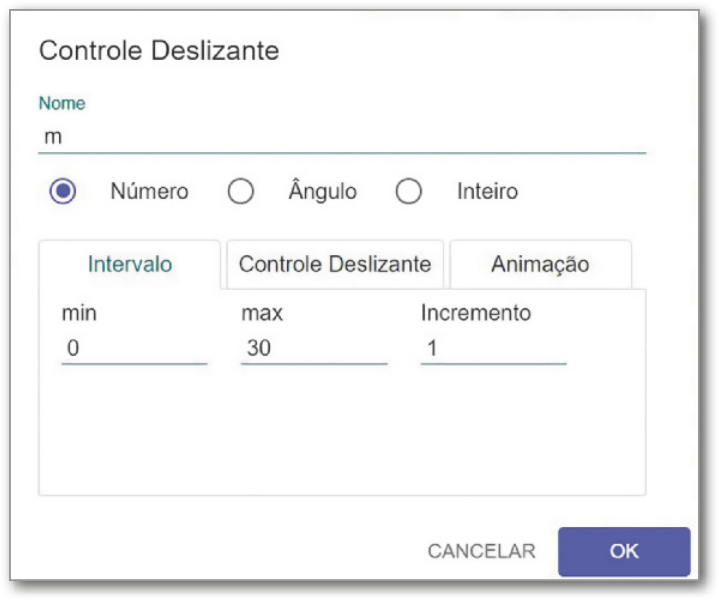
V. Na caixa de ferramentas, selecione a ferramenta contrôle Deslizante, ![]() . Em seguida, clique em qualquer lugar na janela de visualização. Uma janela será aberta para formatar esse contrôle deslizante, conforme a figura a seguir. Altere o nome do contrôle deslizante para “m” e ajuste o intervalo para mínimo 0 e mássimo 30, além de deixar o incremento igual a 1; em seguida, clique em OK.
. Em seguida, clique em qualquer lugar na janela de visualização. Uma janela será aberta para formatar esse contrôle deslizante, conforme a figura a seguir. Altere o nome do contrôle deslizante para “m” e ajuste o intervalo para mínimo 0 e mássimo 30, além de deixar o incremento igual a 1; em seguida, clique em OK.
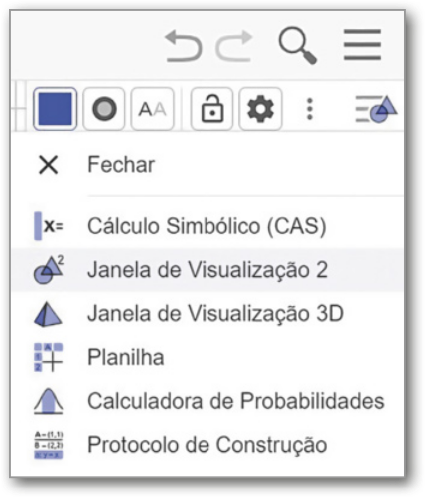
VI. Abra uma segunda janela de visualização. Para isso, clique em ![]() e, em seguida, na opção ⋮, no canto superior direito da janela de visualização, e, depois, selecione Janela de Visualização 2. Feito isso, desabilite os eixos dessa nova janela.
e, em seguida, na opção ⋮, no canto superior direito da janela de visualização, e, depois, selecione Janela de Visualização 2. Feito isso, desabilite os eixos dessa nova janela.
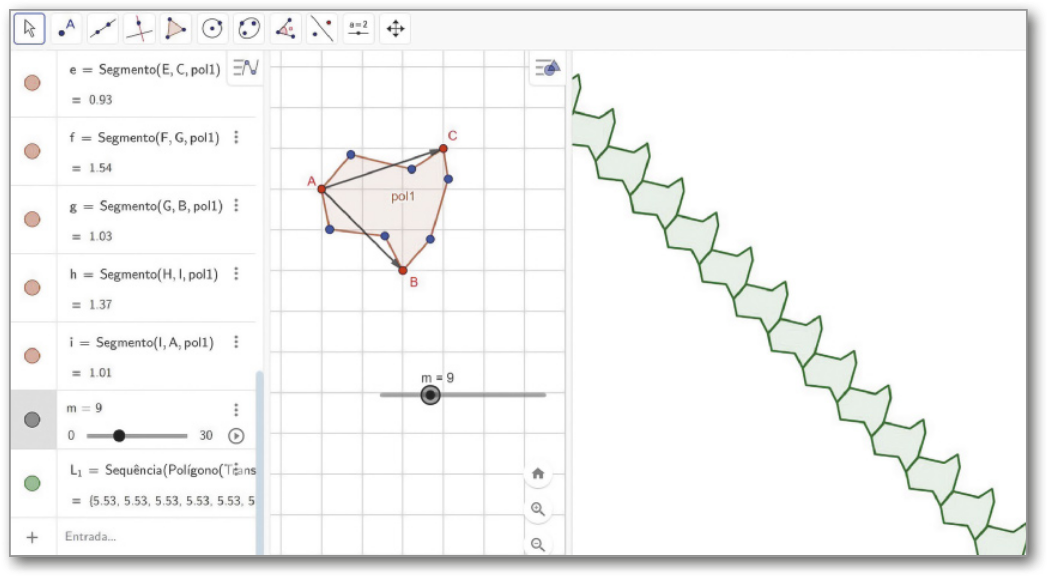
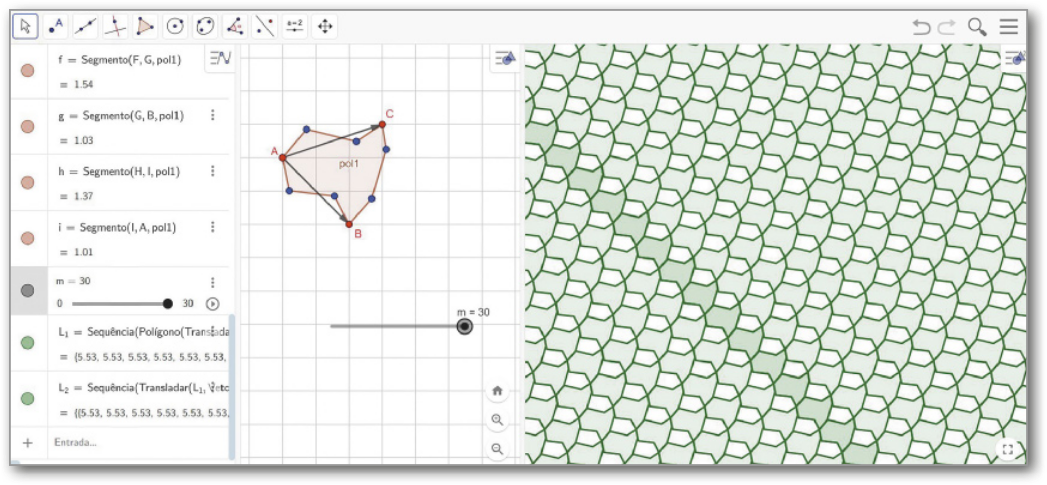
VII. Clique sobre a janela de visualização 2 e, em seguida, no campo de entrada, digite o comando: “L_1=Sequência(Transladar(pol1,u*i),i,−m,m)” e pressione Enter.
Página duzentos e noventa
O significado do cóódigo é o seguinte: “L_1” é o nome dado ao comando; “Sequência” e “Transladar” são funções quê vão repetir o polígono 1; “u*i” indica os múltiplos do polígono; e “−m” e “m” indicam o intervalo em quê ocorrem as repetições.
Na janela de visualização 2, aparecerá uma faixa de figuras quê representa translações do polígono pol1 pelo vetor (conforme o local em quê estiver o contrôle deslizante). Mova o cursor do contrôle deslizante para aumentar ou diminuir a faixa de figuras.
VIII. Clique sobre a janela de visualização 2 e, em seguida, no campo de entrada, digite o comando “L_2=Sequência(Transladar(L_1,v*i),i,−m,m)” e pressione Enter.
Na janela de visualização 2, aparecerá um mosaico de figuras, quê representa translações da faixa ôbitída anteriormente pelo vetor Mova o contrôle deslizante para aumentar ou diminuir o mosaico de figuras.
Página duzentos e noventa e um
IX. Para quê o mosaico não apresente sobreposições ou caso queira mudar o desenho do polígono, ajuste, na janela de visualização 1, a posição de alguns dos vértices do polígono pol1, construídos no passo III, conforme a sua vontade.
A faixa construída pelo comando L1 estará sobreposta à faixa construída pelo comando L2, por isso estará mais escura. Assim, para ocultar uma das linhas de polígono, na janela de Álgebra, clique na bó-linha colorida ao lado direito do comando L1. Caso queira, mude a côr do mosaico nas Configurações do comando L2.
Agora, faça o quê se pede nas atividades a seguir.
1. Faça uma construção seguindo o passo a passo apresentado.
Resposta pessoal.
2. Para m = 1, quantos polígonos aparécem na janela de visualização 2? E para m = 2? E para m = 3?
Para m = 1, aparécem 9 polígonos; para m = 2, aparécem 25 polígonos; para m = 3, aparécem 49 polígonos.
3. escrêeva, em função de n, com 0 ≤ n ≤ 30, quantos polígonos aparécem na janela de visualização 2 quando m = n.
Para m = n, com 0 ≤ n ≤ 30, aparécem (2n + 1)2 polígonos.
4. Deslize o contrôle para m = 30 e dêz-creva o quê ocorre na janela de visualização 2 ao mover o ponto A, B ou C na janela de visualização 1.
O polígono do mosaico tem sua forma alterada, e as linhas de polígonos podem mudar de direção.
Saiba quê...
É possível criar outros tipos de mosaicos no GeoGebra, como o quê está ilustrado a seguir.

Para acessar
• TOMSON, Paulo. Mosaico geométrico. [S. l.]: GeoGebra, c2024. Disponível em: https://livro.pw/wsgbc. Acesso em: 23 out. 2024.
Nesse sáiti, você encontra outros mosaicos quê podem sêr construídos usando o GeoGebra.
Página duzentos e noventa e dois
ATIVIDADES COMPLEMENTARES
1. (hú- hê- érre jota) Considerando o conceito de simetria, obissérve o desenho abaixo:

Os pontos A e B são simétricos em relação à reta s, quando s é a mediatriz do segmento . Observe êste novo desenho:

Em relação à reta s, a imagem simétrica da letra R apresentada no desenho é:
a) ![]()
b) ![]()
c) ![]()
d) ![]()
alternativa c
2. (hú- hê- érre jota) Três pentágonos regulares congruentes e quatro quadrados são unidos pêlos lados conforme ilustra a figura a seguir.
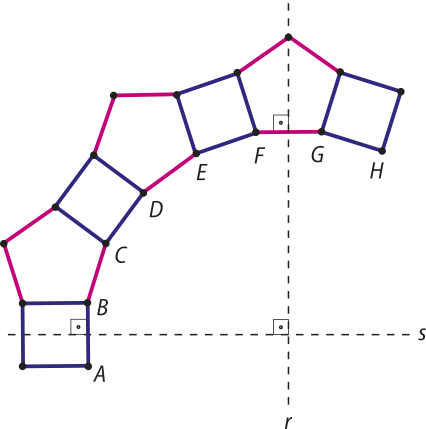
Acrescentam-se outros pentágonos e quadrados, alternadamente adjacentes, até se completar o polígono regular ABCDEFGH… A, quê possui dois eixos de simetria indicados pelas retas r e s.
Se as retas perpendiculares r e s são mediatrizes dos lados e , o número de lados do polígono ABCDEFGH… A é igual a:
a) 18
b) 20
c) 24
d) 30
alternativa b
3. (Fatec-SP) Em um círculo recortado em papel cartão foi feito o desenho de um homem estilizado. Esse círculo foi utilizado para montar uma roleta, conforme a figura 1, fixada em uma parede. Quando a roleta é acionada, o círculo gira livremente em torno do seu centro, e o triângulo indicador permanéce fixo na parede.

Considerando, inicialmente, a imagem do homem na posição da figura 1, obtém-se, após a roleta realizar uma rotação de três quartos de volta, no sentido horário, a figura representada em
a) 
b) 
c) 
d) 
e) 
alternativa e
Página duzentos e noventa e três
4. (Enem/MEC)
Isometria é uma transformação geométrica quê, aplicada a uma figura, mantém as distâncias entre pontos. Duas das transformações isométricas são a reflekção e a rotação. A reflekção ocorre por meio de uma reta chamada eixo. Esse eixo funciona como um espêlho, a imagem refletida é o resultado da transformação. A rotação é o “giro” de uma figura ao redor de um ponto chamado centro de rotação. A figura sofreu cinco transformações isométricas, nessa ordem:
1ª) Reflexão no eixo x;
2ª) Rotação de 90 graus no sentido anti-horário, com centro de rotação no ponto A;
3ª) Reflexão no eixo y;
4ª) Rotação de 45 graus no sentido horário, com centro de rotação no ponto A;
5ª) Reflexão no eixo x.
Disponível em: https://livro.pw/hbnuh. Acesso em: 2 ago. 2012.
Qual a posição final da figura?
a) 
b) 
c) 
d) 
e) 
alternativa c
5. (Saresp) A seguir, são apresentadas a figura 1 e a figura 2, ambas representando quadrados:
Sabendo quê a figura 2 foi ôbitída a partir de duas transformações isométricas da figura 1, assinale a alternativa quê contém as possíveis transformações quê foram utilizadas.
a) Rotação em relação ao centro do quadrado e reflekção em relação a um dos lados do quadrado.
b) Reflexão em relação a uma das diagonais do quadrado e rotação em relação a um dos vértices do quadrado.
c) Translação e reflekção em relação a uma reta paralela a um dos lados do quadrado.
d) Reflexão em relação a uma reta paralela a um dos lados do quadrado e rotação em relação a um dos vértices do quadrado.
e) Rotação em relação ao centro do quadrado e translação.
alternativa e
6. (ESPM-SP) A rotação de um ponto P(x, y) do plano cartesiano em torno da origem é um outro ponto P(minutos)"(x(minutos)", y(minutos)"), obtído pela equação matricial:
,
onde (alfa)" é o ângulo de rotação, no sentido anti-horário. Desse modo, se P = (, 1) e (alfa)" = 60°, as coordenadas de P(minutos)" serão:
a) (−1, 2)
b) (−1, )
c) (0, )
d) (0, 2)
e) (1, 2)
alternativa d
Página duzentos e noventa e quatro
7. (Unicamp-SP) Para construir uma curva “floco de neve”, divide-se um segmento de reta (Figura 1) em três partes iguais. Em seguida, o segmento central sofre uma rotação de 60°, e acrescenta-se um novo segmento de mesmo comprimento dos demais, como o quê aparece tracejado na Figura 2. Nas etapas seguintes, o mesmo procedimento é aplicado a cada segmento da linha poligonal, como está ilustrado nas Figuras 3 e 4.
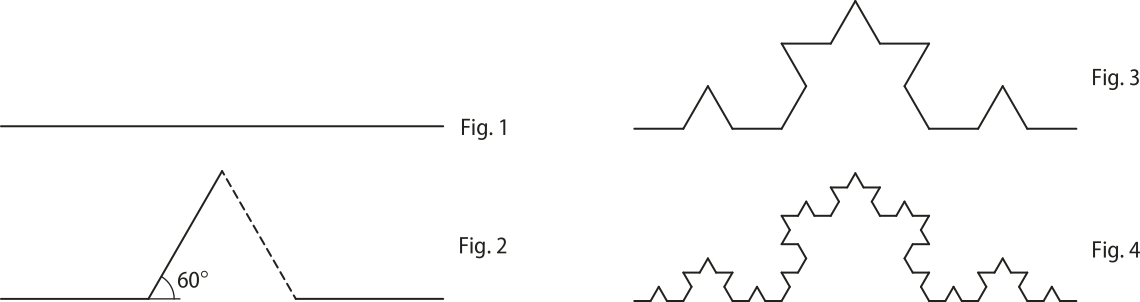
Se o segmento inicial méde 1 cm, o comprimento da curva ôbitída na sexta figura é igual a
a) cm.
b) cm.
c)cm.
d) cm.
alternativa c
8. (Prova Paraná) Uma transformação de homotetia a partir do retângulo JKLM gerou o retângulo FGHI. As dimensões dêêsses polígonos estão apresentadas na figura abaixo.
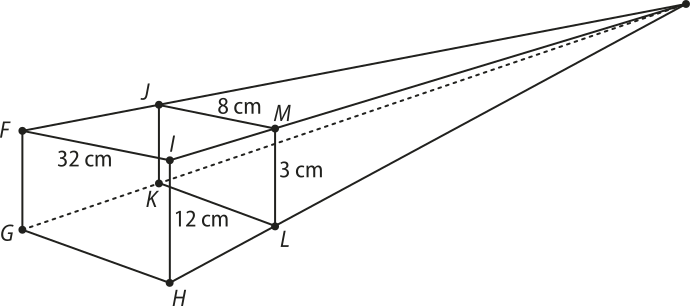
Qual é a razão de homotetia dessa ampliação?
a) 0,25
b) 1,5
c) 4
d) 15
e) 24
alternativa c
9. (ESPM-SP) Considere a matriz M = representando os vértices do triângulo ABC abaixo e a matriz T = como uma matriz de transformação linear.

Assinale a figura quê corresponde à melhor representação do resultado da multiplicação T ⋅ M:
a) 
b) 
c) 
d) 
e) 
alternativa b
Página duzentos e noventa e cinco
10. (Fempar-PR) O pentágono ABCDE da figura abaixo foi ampliado a partir do ponto A, resultando no pentágono AB(minutos)"C(minutos)"D(minutos)"E(minutos)" semelhante ao pentágono inicial.
Sabe-se quê AB = 10 m, BB(minutos)" = 5 m e quê a área do pentágono ABCDE é igual a 220 m2.
Assinale a opção quê indica a área da região sombreada da figura, em m2.
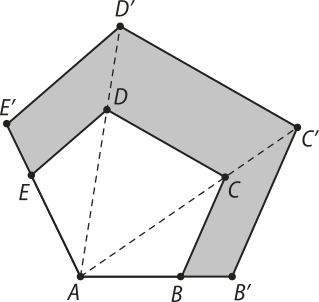
a) 110.
b) 185.
c) 235.
e) 290.
d) 275.
alternativa d
11. (Unésp) Um ponto P, de coordenadas (x, y) do plano cartesiano ortogonal, é representado pela matriz coluna , assim com a matriz coluna representa, no plano cartesiano ortogonal, o ponto P de coordenadas (x, y).
Sendo assim, o resultado da multiplicação matricial é uma matriz coluna quê, no plano cartesiano ortogonal, necessariamente representa um ponto quê é
a) uma rotação de P em 180° no sentido horário, e com centro em (0, 0).
b) uma rotação de P em 90° no sentido anti-horário, e com centro em (0, 0).
c) simétrico de P em relação ao eixo horizontal x.
d) simétrico de P em relação ao eixo vertical y.
e) uma rotação de P em 90° no sentido horário, e com centro em (0, 0).
alternativa b
PARA REFLETIR
Neste Capítulo, estudamos as transformações geométricas. Conhecemos as isometrias denominadas reflekção, translação e rotação, quê são transformações geométricas quê preservam a distância entre dois pontos. Estudamos também a composição de transformações.
Trabalhamos as homotetias, quê são as transformações geométricas quê associam polígonos semelhantes, e, por fim, algumas transformações isométricas por meio de matrizes.
Nas páginas de abertura, conhecemos um pouco sobre os bordados de Buriti dos lópes e, na introdução do Capítulo, foi apresentada a imagem de uma obra de é-chêr.
Agora, vamos refletir sobre as aprendizagens do Capítulo 7:
• Depois de ter estudado o conteúdo dêste Capítulo, você tem um olhar diferente sobre bordados e mosaicos? Explique.
• Cite pelo menos três conteúdos apresentados ao longo dêste Capítulo. Você já conhecia algum deles?
• Cite alguns objetos do dia a dia quê remetam à ideia de simetria. Justifique sua resposta.
• Explique a diferença entre congruência e semelhança e a relação dêêsses conceitos com as isometrias e as homotetias.
• Explique como a sua produção inspirada em uma obra da artista êstér Mahlangu auxiliou sua compreensão sobre transformações isométricas e simetrias.
• Explique como o trabalho feito com o GeoGebra contribuiu para o seu entendimento das translações.
Respostas pessoais.
Página duzentos e noventa e seis