Página 12
UNIDADE 1
A CIÊNCIA DO UNIVERSO
O Universo, formado por diversos elementos fascinantes, sempre despertou curiosidade e muitas reflexões na humanidade. Do que ele é feito? Como surgiu e evoluiu? Como as estruturas do Universo se organizam? O que originou a vida? Algumas respostas para esses questionamentos foram construídas e modificadas ao longo do tempo à medida que a sociedade foi se desenvolvendo e a Ciência evoluindo.
O avanço da Ciência, com auxílio de inovações tecnológicas, permitiu o desenvolvimento de instrumentos que podem ser colocados fora da atmosfera terrestre e são capazes de capturar imagens detalhadas de estruturas do Universo. Naturalmente, à medida que algumas questões são solucionadas, outras perguntas surgem, impulsionando e incentivando ainda mais os cientistas e estudiosos na busca de novas explicações.
Nesta unidade, serão apresentadas uma breve evolução dos conceitos que levaram à formação da Ciência atual, a teoria do Big Bang e algumas leis relacionadas ao movimento dos objetos e dos planetas.
a ) Em sua opinião, como a Ciência influencia a sociedade e como a sociedade influencia a Ciência?
b ) Qual é a sua opinião sobre o surgimento do Universo?
c ) Como você acha que o Sistema Solar se formou? Converse com seus colegas sobre o assunto.
d ) Essa fotografia foi registrada por um telescópio espacial que orbita o Sol. Por que esse telescópio não se perde no espaço?
Respostas nas Orientações para o professor.
Nesta unidade, vamos estudar...
- evolução dos conceitos da Física;
- origem e evolução do Universo;
- evolução estelar;
- formação dos sistemas planetários;
- leis de Kepler;
- leis de Newton;
- gravitação universal;
- queda livre e lançamento de projéteis.
Página 13

Página 14
CAPÍTULO1
História da Ciência
Evolução dos conceitos da Física
Indícios históricos mostram que os povos observavam o céu e os astros para auxiliar em atividades do cotidiano como o plantio e a colheita de alimentos.
Diversos povos observaram e registraram os fenômenos dos eclipses. Os Tupi-Guarani, por exemplo, acreditam que a Onça Celeste persegue os irmãos Sol e Lua e, por isso, fazem barulho nas ocasiões dos eclipses solares e lunares, para espantar a Onça, impedindo-a de devorar esses e outros astros e deixar a Terra na escuridão. Já alguns filósofos chineses explicavam os eclipses pelo crescimento ou diminuição das "forças" Yin (escuridão) e Yang (luz), apesar de alguns registros mostrarem que os chineses já associavam os eclipses aos movimentos do Sol, da Terra e da Lua.
Atualmente, sabemos que o eclipse solar ocorre quando a Lua se posiciona entre o Sol e a Terra, e o eclipse lunar umbral quando a Lua passa pelo cone de sombra projetado pelo planeta.

Na Grécia antiga, por exemplo, os filósofos estudavam vários elementos ao seu redor e buscavam explicações para os fenômenos naturais. Assim, o conhecimento englobava diversas áreas. Atualmente a área do conhecimento que estuda e descreve os fenômenos naturais que ocorrem no Universo, tanto bióticos quanto abióticos, é denominada Ciências da Natureza. Essa área engloba várias áreas de estudo, entre elas a Química (do latim chimia = mistura), a Física (do grego physis = natureza) e a Biologia (do grego bios = vida e logia = estudo).
1. Qual é a importância de conhecer as origens e a construção do conhecimento científico?
Resposta pessoal. O objetivo desta questão é levar os estudantes a refletir sobre a história da humanidade, incluindo a história da Ciência, para que possam compreender como determinado conceito é construído, ou modificado, chegando a sua definição nos dias atuais.
Para chegarmos ao conhecimento científico atual, o pensamento e as explicações passaram por diversas modificações. Na Pré-História, período que se estende até por volta de 3500 a.C., os conhecimentos e as técnicas eram desenvolvidos de acordo com a necessidade de sobrevivência da época. Por exemplo, os povos indígenas brasileiros explicavam o fogo normalmente observado em terrenos pantanosos e cemitérios, por meio da lenda do boitatá (ou "serpente de fogo", do tupi-guarani). Segundo essa lenda, o boitatá protege as matas das pessoas que provocam queimadas.
A explicação científica para tal fenômeno é que a decomposição da matéria orgânica presente nos pântanos e cemitérios libera gases. Estes, na presença do gás oxigênio abre parênteses O subscrito 2 fecha parênteses do ar, entram em combustão espontânea, produzindo o chamado fogo-fátuo.
Percebemos, assim, que as explicações mitológica e científica para um mesmo fenômeno natural dependem do contexto em que o observador se encontra.
Imagem sem proporção e em cores fantasia.

Página 15
A transição para o pensamento racional começou na Antiguidade (3500 a.C.-476 d.C.), quando diversas civilizações desenvolveram um padrão de pensamento um pouco mais distante da lógica mística✚, mas que ainda assim era marcado pela mitologia✚, ou seja, pensamentos racional e místico eram utilizados em conjunto.
Entre as civilizações da Antiguidade, a sociedade egípcia foi uma das mais surpreendentes em termos de conhecimento científico. De acordo com o físico, químico e historiador Cheikh Anta Diop (1923-1986), os povos do Egito, ou Kemet (terra negra ou terra de homens negros), já produziam conhecimento nas áreas da Medicina, Ciência, Filosofia e História muito antes dos filósofos gregos.
Esses conhecimentos eram transmitidos em instituições chamadas Per Ankh (Casas da Vida), que funcionavam de modo semelhante a uma universidade, com arquivo, biblioteca e oficina de cópia de papiros.
Alguns saberes do Egito antigo foram organizados para facilitar o dia a dia, como a padronização de pesos e medidas, a escrita por meio de hieróglifos e o domínio da Matemática. Esses conhecimentos permitiram, por exemplo, a construção de grandes monumentos, como as pirâmides, existentes até hoje.

Os egípcios realizavam o processo de mumificação, prática na qual um corpo era embalsamado para evitar sua decomposição. Acredita-se que essa técnica foi fundamental para o conhecimento da anatomia do corpo humano e do tratamento de doenças. Existem evidências que indicam que os egípcios antigos utilizavam próteses de membros e realizavam cirurgias cranianas e tratamentos dentários.

Já na Astronomia, o conhecimento egípcio relacionado aos planetas, às constelações e aos movimentos do Sol e da Lua era voltado, principalmente, para a medição do tempo. O calendário organizado pelos egípcios é considerado o mais avançado dos tempos antigos, prevendo as estações do ano e alguns eclipses.
Além da sociedade egípcia, outras civilizações antigas, como a chinesa, a árabe, a indiana e a grega, contribuíram para a construção do conhecimento que temos hoje.
Os chineses desenvolveram grande conhecimento sobre Astronomia, Geologia e Medicina. Eles consideravam que o Universo seria um grande ser vivo, composto de cinco elementos básicos: água, metal, madeira, fogo e terra. Entre as invenções chinesas utilizadas até hoje, destacam-se a bússola, os relógios e o papel.
2. Como a medição do tempo, a previsão de fenômenos e tantas outras descobertas científicas influenciaram a organização das atividades diárias das sociedades?
Resposta pessoal. Espera-se que os estudantes respondam que, quando existe a possibilidade de reunir conhecimentos, organizá-los e, assim, prever a ocorrência de diversos fenômenos, as atividades diárias também podem ser organizadas.
Página 16
A cultura ocidental foi bastante influenciada pela cultura grega, pois uma de suas características foi a busca por racionalizar a compreensão do mundo e dos fenômenos naturais. Por sua vez, a civilização grega sofreu influência da cultura egípcia, em razão de viagens de filósofos e historiadores gregos ao Egito.
Uma das figuras gregas mais significativas foi o filósofo Aristóteles (384 a.C. -322 a.C.), um dos primeiros a defender o método lógico de investigação em suas observações e a utilização de experiências sensoriais com o mundo real, necessárias para obter regras gerais ao descrever a natureza.
Assim, Aristóteles, além de observar os movimentos regulares dos astros no céu e de corpos na Terra, estudou os elementos fundamentais que formavam o Universo e contribuiu para outras áreas das Ciências da Natureza. Por exemplo, ele descreveu características de alguns animais e nomeou cerca de 500 espécies, além de estudar a vida marinha, a Embriologia e a anatomia humana e de outros animais.
Imagens sem proporção.

Os gregos também se dedicaram à Matemática. Pitágoras (por volta de 570 a.C.-490 a.C.) e seus seguidores, por exemplo, afirmavam que tudo poderia ser descrito por meio de números.
Os pitagóricos desenvolveram estudos sobre as escalas musicais por meio de princípios matemáticos, quando notaram a relação entre o comprimento de uma corda vibrante ou de uma coluna de ar e as notas musicais. Uma corda com certo comprimento emitia uma nota, já a mesma corda com metade do comprimento emitia a mesma nota, mas uma oitava acima.

A filósofa egípcia Hipátia de Alexandria (370-415) é considerada a primeira mulher matemática da história. Ela foi diretora de uma escola em Alexandria, onde se destacou em várias disciplinas, incluindo Matemática, Astronomia e Filosofia neoplatônica. Além de suas realizações acadêmicas, Hipátia é lembrada por seu papel como educadora e defensora do racionalismo e da investigação científica, atraindo estudantes de toda a região do mar Mediterrâneo. Durante sua vida, ela escreveu vários textos sobre Matemática e contribuiu com sua visão científica para diversas pesquisas astronômicas da época.
Entre os estudiosos das regiões atualmente conhecidas como Oriente Médio e Ásia, o filósofo persa Avicena (Ibn Sina) (980-1037) se destacou ao desenvolver um manuscrito sobre Medicina que se tornou referência na área durante vários séculos em todo o mundo. Na Índia, registros de mais de dois milênios indicam um amplo e diversificado conhecimento do corpo humano e seu funcionamento, reunidos sob a chamada medicina aiurvédica.
3. Em sua opinião, o desenvolvimento e o aperfeiçoamento tecnológico são importantes para as Ciências? Justifique sua resposta.
Resposta pessoal. Espera-se que os estudantes respondam que sim, pois a tecnologia fornece aos cientistas ferramentas práticas que possibilitam um maior aprofundamento das pesquisas científicas.
Página 17
Dessa maneira, podemos perceber que o conhecimento a respeito da natureza se modificou ao longo do tempo, sendo construído por diferentes povos. No entanto, a revolução que impulsionou a visão científica ocidental como conhecemos hoje aconteceu na Idade Moderna (1453-1789). O Renascimento, período compreendido entre os séculos XIV e XVI, se iniciou na Itália e ao longo dos anos se estendeu pelo resto da Europa. Ele foi marcado pela retomada de muitos conhecimentos da Antiguidade grega e pela transformação da economia, da política, da Literatura, das Artes e das Ciências.
Nesse período, surgiram artistas reconhecidos no mundo todo, como os italianos Leonardo da Vinci (1452-1519), Michelangelo Buonarroti (1475-1564), Rafael Sanzio (1483-1520) e Lavinia Fontana (1552-1614).
Além das Artes, vários acontecimentos estão relacionados ao período do Renascimento, como as Grandes Navegações, a invenção da imprensa e a abertura de universidades.

Nessa época, ocorreram aperfeiçoamentos em diversas técnicas de navegação, o que permitiu, por exemplo, que as caravelas pudessem navegar contra os ventos com mais eficiência. Alguns instrumentos essenciais para a navegação tiveram melhorias tecnológicas, como a bússola, o astrolábio náutico e o quadrante.
A bússola foi um dos instrumentos mais importantes para o desenvolvimento da navegação. Nela existe uma agulha magnetizada, que se alinha com o campo magnético da Terra, indicando a orientação norte-sul da Terra.
O astrolábio é um instrumento que permite medir a altura dos astros no céu em relação ao horizonte. Ele é formado por um disco com a borda graduada, um anel de suspensão e uma espécie de ponteiro, e foi muito utilizado nas navegações como instrumento de orientação, baseando-se na determinação da posição das estrelas no céu para o cálculo da latitude dos navios.
Já o quadrante foi um instrumento muito utilizado pelos navegantes portugueses por volta do século XV. Ele era um instrumento de formato de um quarto de círculo, com duas espécies de miras perfuradas na parte reta inferior e um fio de prumo preso ao centro do arco. O quadrante também era utilizado para medir a altura dos astros, auxiliando na orientação dos navegadores.
Essas inovações permitiram que as embarcações pudessem navegar cada vez mais longe, possibilitando que os povos europeus chegassem a novas terras, como as Américas, a costa africana, a Ásia e o Pacífico, contribuindo para a expansão de seus domínios e seu comércio e para o acúmulo de capitais dos exploradores.
Imagens sem proporção.



Página 18
No contexto das Grandes Navegações, os portugueses estavam em disputa com a Espanha por territórios e rotas comerciais. Investindo nas navegações, o reino de Portugal acabou se tornando uma potência marítima, colonizando diversos territórios nas Américas, na África e na Ásia, incluindo o Brasil.
A expedição dos portugueses desembarcou no Brasil em 22 de abril de 1500, em um local atualmente chamado Santa Cruz Cabrália, na Bahia, tendo contato com os indígenas.

Também durante o período do Renascimento ocorreu a chamada "revolução astronômica", que redefiniu diversas propostas feitas na Antiguidade e modificou as concepções europeias acerca do Sol e do Sistema Solar.
Até então, o modelo astronômico mais aceito entre os filósofos da época era o consolidado pelo matemático e geógrafo egípcio Ptolomeu (100-170), que ficou conhecido como modelo geocêntrico✚. Esse modelo já era conhecido por outros filósofos da Antiguidade, mas foi Ptolomeu o responsável por formalizar a teoria. Nela, as estrelas estariam fixas em uma esfera que gira em torno da Terra, além do Sol, da Lua e de outros astros conhecidos que também orbitariam ao redor da Terra.
O astrônomo polonês Nicolau Copérnico (1473-1543) sugeriu outro modelo para o Sistema Solar no qual a Terra e os outros planetas executavam um movimento orbital circular ao redor do Sol, chamado de modelo heliocêntrico✚. Esse modelo também já havia sido proposto anteriormente, mas foi Copérnico quem o sistematizou e o popularizou.
O modelo heliocêntrico não foi aceito prontamente. Todavia, o desenvolvimento do telescópio e a contribuição de outros cientistas, como o astrônomo dinamarquês Tycho Brahe (1546-1601), o astrônomo e matemático alemão Johannes Kepler (1571-1630) e o cientista italiano Galileu Galilei (1564-1642), possibilitaram que o modelo heliocêntrico ganhasse força.
Imagem sem proporção e em cores fantasia.

O ano da morte de Galileu foi marcado pelo nascimento de outro importante nome da Ciência, o cientista inglês Isaac Newton (1643-1727). Newton se dedicou ao estudo da Matemática, Óptica, Mecânica, Química e Astronomia, descrevendo fundamentos de sua teoria da luz, da gravitação e dos movimentos planetários. Em 1687, lançou o livro Philosophiae naturalis principia mathematica, Princípios matemáticos da filosofia natural, ou simplesmente Principia, considerado uma das maiores obras científicas de todos os tempos. Nele, Newton descreveu toda a sua fundamentação teórica a respeito do que rege os corpos em movimento. A obra representa um dos pilares da chamada Física clássica.

Página 19
Essa confluência de exploração marítima e inovação científica marcou o início da era moderna, estabelecendo as bases para o desenvolvimento tecnológico e cultural que moldaria o mundo nos séculos seguintes.
No final do século XIX, acreditava-se que todos os fenômenos naturais poderiam ser descritos pela Ciência desenvolvida até então. No entanto, alguns fenômenos continuavam sem explicação, como o efeito fotoelétrico e a emissão de radiação do corpo negro.
A busca pela compreensão desses problemas abriu margens para descobertas inimagináveis até esse período, o que levou, no século XX, à chamada Física moderna, com proposições teóricas que se voltaram para o estudo dos fenômenos subatômicos, que contribuíram para o desenvolvimento das telecomunicações, a eletrônica e os estudos sobre o Universo. A Física moderna levou à fundamentação da teoria da relatividade e da teoria quântica.
A teoria da relatividade, proposta em 1905 pelo físico alemão Albert Einstein (1879-1955), trata sobre o movimento relativo e os efeitos observados na matéria a altas velocidades, próximas à velocidade da luz, apresentando uma nova interpretação para o espaço e o tempo.
Já a teoria quântica está relacionada ao estudo da matéria em escala atômica e subatômica. Essa teoria serve como base para outros campos de estudo da Física, como Física atômica, Física de partículas, Física nuclear e Física molecular, e campos da Química e da Computação.

O desenvolvimento de novas teorias é resultado do trabalho de cientistas, pesquisadores, entre outros profissionais. Entre eles, devemos valorizar a contribuição de inúmeras mulheres para a Ciência, que, infelizmente, tiveram seus trabalhos diminuídos ou invisibilizados ao longo da história.
A física e astrônoma estadunidense Sarah Frances Whiting (1847-1927), por exemplo, foi a fundadora do primeiro laboratório de graduação em Física para mulheres nos Estados Unidos, trabalhando para incentivar o ingresso de mulheres no meio científico. Ela foi professora da astrônoma estadunidense Annie Jump Cannon (1893-1941), responsável pela criação do sistema de classificação de estrelas utilizado até hoje. Já a primeira brasileira a concluir um doutorado em Física foi Sonja Ashauer (1923-1948), defendendo uma tese na área de Eletrodinâmica quântica.


Com a contribuição de inúmeros profissionais, homens e mulheres, para o seu desenvolvimento ao longo da história, a Ciência pode ser entendida como uma atividade humana construída com base na observação dos fenômenos naturais e na tentativa de explicá-los racionalmente. O conhecimento científico é passível de verificações, testes e substituições. Como toda atividade humana, a Ciência é dinâmica e está em constante evolução.
Página 20
LIGADO NO TEMA
Uso do método científico no cotidiano
O método científico é a análise sistemática praticada como processo de investigação sobre o funcionamento e/ou a causa de determinada situação. Esse método é muito utilizado na comunidade científica. Por exemplo, foi por meio desse método que o médico inglês John Snow (1813-1858) concluiu que a transmissão dos casos de cólera acontecia pela ingestão de água contaminada.
No entanto, o método científico pode ser aplicado em diversas situações da vida cotidiana, como na resolução de um problema doméstico ou no desenvolvimento e melhoramento de um produto.
Confira a situação a seguir.

Ao tentar acender a lâmpada de uma luminária, Joana verificou que ela não acendeu.
Imagens desta página sem proporção e em cores fantasia.
1. A fim de fazê-la funcionar corretamente, Joana fez uma observação detalhada da luminária. Ela verificou se o interruptor estava na posição correta e se o cabo estava conectado na tomada.

2. Com base nisso, Joana então formulou a pergunta: por que a luminária não acendeu mesmo com o interruptor na posição correta e o cabo devidamente conectado na fonte de energia?

3. Para responder à pergunta, Joana formulou uma hipótese: a lâmpada da luminária poderia estar queimada.

4. Assim, testando essa hipótese, ela decidiu substituir a lâmpada antiga por uma nova e ligou a luminária novamente, verificando que o problema havia sido resolvido, pois a luminária voltou a funcionar corretamente.

Por isso, por meio da análise baseada em evidências projetada pelo método científico, é possível obter conclusões mais confiáveis e mais assertivas, evitando, assim, conclusões precipitadas.
a ) Quais seriam as outras possíveis hipóteses para o problema no funcionamento da luminária?
Resposta pessoal. Espera-se que os estudantes mencionem a hipótese de existir algum problema na instalação dos itens que compõem a luminária, como fio rompido ou mau contato do interruptor.
b ) Caso Joana não houvesse corrigido o problema da luminária substituindo a lâmpada antiga por uma nova, qual seria a próxima etapa que ela deveria seguir?
Resposta: Elaboração de novas hipóteses.
Página 21
ATIVIDADES
1. O filósofo grego Anaximandro (610 a.C.-547 a.C.) sugeriu, na Antiguidade, que os trovões eram causados pelos ventos e que os raios eram produzidos quando nuvens se dividiam. Antes dessa proposição, raios e trovões eram comumente considerados manifestações místicas, de poderes ocultos.
a ) Faça um comparativo entre as explicações dadas aos fenômenos naturais ao longo da Antiguidade. O que você conclui sobre a maneira como os fenômenos eram explicados?
Resposta: As percepções de que o mundo era controlado por forças místicas que se manifestavam sob a forma de trovões, raios, enchentes, doenças, entre outros fenômenos, foram se transformando à medida que a ciência se desenvolveu, levando à racionalização de diversas ideias que anteriormente recorriam a explicações misteriosas.
b ) Atualmente, qual é a explicação científica para a ocorrência de raios e trovões? Faça uma pesquisa na biblioteca da escola e/ou em sites da internet sobre esses fenômenos naturais para responder a esta questão.
Resposta: Os raios são descargas elétricas entre nuvens ou entre nuvens e o solo, quando cargas elétricas acumuladas se deslocam emitindo luz. O ar ao redor do deslocamento das cargas elétricas é aquecido e se expande, causando o estrondo sonoro característico do trovão.
2. Pesquise na internet dois cientistas brasileiros e elabore uma pequena biografia de cada um. Cite os nomes, as idades e as áreas de pesquisa em que atuam ou atuaram e, se possível, algum trabalho de alta relevância de autoria deles.
Resposta pessoal. Incentive os estudantes a buscar por nomes de cientistas brasileiros, destacando que a ciência brasileira desenvolve trabalhos significativos. Além disso, conduza a pesquisa de nomes de cientistas mulheres, já que poucos são mostrados na história.
3. Leia a seguir um trecho da entrevista com o historiador da Ciência, filósofo e físico francês Michel Paty (1938 -). A entrevista foi realizada quando Paty visitou o Brasil, em novembro de 2013.
[...] Em seu trabalho, o senhor já explorou muito as ideias de Einstein e Poincaré a respeito da criatividade, do estilo científico e do papel da invenção na Ciência. Fazendo um paralelo com os dias atuais, qual o papel da criatividade e da invenção na Ciência contemporânea?
Paty - A grande dificuldade para responder a essa pergunta está na forma que a pesquisa científica tomou a partir da segunda metade do século 20. No tipo de Ciência que temos hoje em domínios importantes, a Big Science, o trabalho é muito coletivo e as experiências são de alta tecnologia, tanto na Física, na Química e na Astronomia quanto na Biologia e na Neurociência. Há uma enorme mobilização de pesquisadores, instituições, equipamentos e recursos. Parece ser mais difícil perceber aqui uma originalidade de contribuição dos pesquisadores tomados individualmente.
Porém, se olharmos os conhecimentos produzidos por esse tipo de pesquisa, eles não deixam de ter a mesma natureza de quando o trabalho científico era mais individual [...].
A CIÊNCIA criativa. Ciência Hoje, 11 dez. 2013. Disponível em: https://s.livro.pro/2hj2un. Acesso em: 19 jul. 2024.
O que se pode concluir, com base na resposta de Paty, a respeito da diferença entre fazer Ciência atualmente e antes do século XX? Converse com seus colegas e elabore um texto argumentativo com suas conclusões.
Resposta pessoal. Espera-se que os estudantes respondam que, em razão da globalização e da facilidade de comunicação entre as pessoas a nível mundial, as pesquisas adquirem um caráter coletivo.
4. Leia o trecho do texto apresentado e responda às questões.
Pode-se concluir, então, que o mito é a primeira forma que o ser humano utilizou para dar sentido ao mundo. Ele é um tipo de saber afetivo, coletivo e dogmático, trata-se de um relato, construído coletivamente, ainda que sem a consciência dessa construção. [...] Mas, a partir de um dado momento do processo histórico, essa explicação mítica, essa forma de saber de si e do mundo, começa a ser questionada por aqueles que seriam conhecidos como os filósofos, os pré-socráticos, preocupados em buscar a arkhé, o princípio fundamental das coisas. Doravante, são eles que buscam dar uma explicação sustentada em argumentos racionais para o existente.
FERNANDES, Vladimir. A transição do mito à filosofia e o processo político-formativo do cidadão grego. Hipótese, Itapetininga, v. 2, n. 1, 2016. p. 86. Disponível em: https://s.livro.pro/44qysm. Acesso em: 25 jul. 2024.
a ) Reescreva os trechos do texto que tratam da diferença entre os pensamentos mitológico e filosófico.
Resposta: Espera-se que, para o pensamento mitológico, os estudantes reescrevam: "Ele é um tipo de saber afetivo, coletivo e dogmático, trata-se de um relato, construído coletivamente, ainda que sem a consciência dessa construção". E para o pensamento filosófico: "[...] buscam dar uma explicação sustentada em argumentos racionais para o existente".
b ) Faça uma pesquisa e cite um fenômeno natural que tenha explicações mitológica e científica. Produza um texto com essas informações e o apresente aos colegas.
Resposta pessoal. Os estudantes podem citar, por exemplo, o mito grego que explica as ondas de ressaca do mar como resultado da ação do deus Poseidon, espetando o mar com seu tridente.
Página 22
5. Leia o trecho do texto a seguir e responda às questões.
[…]
Além da orientação geográfica, um dos principais objetivos práticos da astronomia indígena era sua utilização na agricultura. Os indígenas associavam as estações do ano e as fases da Lua com a biodiversidade local, para determinarem a época de plantio e da colheita, bem como para a melhoria da produção e o controle natural das pragas. Eles consideram que a melhor época para certas atividades, tais como, a caça, o plantio e o corte de madeira, é perto da lua nova, pois perto da lua cheia os animais se tornam mais agitados devido ao aumento de luminosidade, por exemplo, a incidência dos percevejos que atacam a lavoura.
[…]
Os indígenas que habitam o litoral também conhecem a relação das fases da Lua com as marés. Eles associam as marés às estações do ano para a pesca artesanal. Em geral, quando saem para pescar, seja no rio ou no mar, já sabem quais as espécies de peixe mais abundantes, em função da época do ano e da fase da Lua. […]
AFONSO, Germano Bruno. Astronomia indígena. In: REUNIÃO ANUAL DA SBPC, 61., 2009, Manaus. Anais... Manaus: UFAM, 2009. p. 2-3. Disponível em: https://s.livro.pro/fnua84. Acesso em: 24 jul. 2024.
a ) Como a observação do céu e o estudo dos fenômenos astronômicos puderam contribuir para o desenvolvimento da agricultura?
Resposta: Eles permitiram a criação dos calendários, sendo possível prever as estações do ano e quais seriam as melhores épocas para o plantio e a colheita.
b ) Como os antigos agricultores utilizavam as estrelas e os ciclos lunares para determinar os melhores períodos para plantar e colher suas culturas?
Resposta: Pela observação de padrões no céu, como o surgimento de certas constelações, que sinalizavam mudanças sazonais.
c ) Como as tecnologias modernas de satélites e a observação astronômica contribuem para o monitoramento do clima e do solo, ajudando no desenvolvimento sustentável da agricultura?
Resposta nas Orientações para o professor.
6. A proposta da existência do átomo se deu já no século V pelos filósofos gregos Leucipo (500 a.C.-430 a.C.) e Demócrito (460 a.C.-370 a.C.). A palavra átomo vem do grego a = não e tomo = partes, e significa "o que não pode ser cortado". Para eles, toda a matéria seria formada por minúsculas partículas indivisíveis. Entretanto, essas ideias eram apenas hipóteses não testadas.
Em 1803, o químico inglês John Dalton (1766-1844) propôs que os átomos seriam partículas esféricas maciças. Os átomos de um tipo de elemento químico seriam todos iguais e os elementos se diferenciariam por terem átomos de massas e tamanhos diferentes.
Apesar de o modelo atômico de Dalton ter auxiliado no avanço do conhecimento científico da época, ele foi refutado quando, em 1898, o físico inglês Joseph John Thomson (1856-1940) descobriu e identificou o elétron como subpartícula do átomo. Ele propôs um novo modelo para o átomo, onde o núcleo seria formado por uma esfera de carga elétrica positiva com os elétrons, de carga elétrica negativa, distribuídos dentro dela. Assim como o modelo de Dalton, os compostos seriam formados por átomos agrupados.
Em 1908, o físico neozelandês Ernest Rutherford (1871-1937) e seus estudantes, o físico alemão Hans Geiger (1882-1945) e o físico inglês Ernest Marsden (1889-1970), realizaram uma série de experimentos a fim de investigar a estrutura do átomo. Eles lançaram um feixe de partículas de carga positiva sobre uma folha muito fina feita de ouro. Grande parte dessas partículas atravessou a folha sem sofrer desvios em sua trajetória, uma pequena parte sofria pequenos desvios e poucas delas eram desviadas em grandes ângulos. O modelo atômico mais aceito até então, proposto por Thomson, não explica o experimento feito por Rutherford e seus estudantes.
a ) Explique por que o modelo atômico de Thomson é incompatível com o experimento feito por Rutherford e seus estudantes.
Resposta: Caso a matéria fosse composta de átomos esféricos agrupados, não haveria espaço para que a maior parte das partículas positivas do feixe atravessasse a folha de ouro.
b ) Com base nos resultados dos experimentos da folha de ouro de Rutherford, quais conclusões sobre a estrutura atômica podem ser obtidas?
Resposta nas Orientações para o professor.
7. A física, como ciência fundamental, desempenha um papel crucial na interdisciplinaridade, integrando-se a diversas áreas do conhecimento. Essa interação entre diferentes áreas do saber possibilita a criação de mais tecnologias, a compreensão mais profunda dos processos naturais e o desenvolvimento de soluções inovadoras para os desafios da sociedade.
Pesquise e cite exemplos em que a Física se conecta com outras disciplinas. Para cada exemplo, descreva como essa integração ocorre e qual é a importância dela.
Resposta nas Orientações para o professor.
Página 23
CAPÍTULO2
Origem e evolução do Universo
A teoria do Big Bang
Leia o trecho de reportagem a seguir sobre a pesquisa de um astrônomo brasileiro relacionada à formação do Sistema Solar.
A pesquisa [...] sugere que, nos primeiros milhares de anos durante o processo de formação do Sol, nossa estrela estaria circundada por três anéis concêntricos, repletos de detritos de gelo e poeira, com tamanhos e características distintos. Estes anéis, posteriormente, teriam dado origem aos diferentes corpos situados em diferentes regiões e que são responsáveis pela configuração, ou arquitetura, que observamos no Sistema Solar hoje.
PALADINO, Guilherme. Existência de diversos anéis ao redor do Sol no passado pode explicar atual arquitetura do Sistema Solar, sugere pesquisa de astrônomo brasileiro. Jornal da Unesp, 9 maio 2022. Disponível em: https://s.livro.pro/j93xh7. Acesso em: 22 jul. 2024.
Entender a origem do Universo e do Sistema Solar é uma tarefa complexa, pois depende de observações que nos forneçam evidências indiretas de como esses eventos ocorreram.
A teoria mais aceita entre os cientistas para explicar a origem do Universo teve início com as descobertas do astrônomo estadunidense Edwin Hubble (1889-1953). Ele observou que as galáxias✚ distantes se afastam umas das outras e que, quanto maior a distância entre elas, maior sua velocidade de afastamento.

Tal teoria sugere que o Universo se expandiu a partir de um ponto material extremamente quente e denso, o qual continha toda a energia existente no Universo atual. Essa teoria foi batizada de Big Bang por seus opositores de forma pejorativa, pois a ideia de que o Universo teve um início era rejeitada pela grande maioria da comunidade científica da época.
Alguns conceitos da teoria do Big Bang foram apresentados pelo padre e físico belga Georges Lemaître (1894-1966), que usou modelos baseados nas equações do físico alemão Albert Einstein (1879-1955) para a relatividade geral✚. Lemaître propôs que o Universo tinha um tempo passado finito e que começou a partir de uma região pequena e compacta, a qual chamou de átomo primordial, que se expandiu e evoluiu com o tempo.


A teoria do Big Bang foi aperfeiçoada pelo físico estadunidense George Gamow (1904-1968). Ele propôs que o estado inicial do Universo permitiria a síntese de todos os núcleos atômicos. Posteriormente, verificou-se que essa síntese inicial só produziria os núcleos mais simples, como o hidrogênio (H), o hélio (H e) e o lítio (Li). Gamow também previu que o Big Bang deixaria uma radiação✚ residual espalhada por todo o Universo.
- Galáxias:
- grandes aglomerações de estrelas, planetas, gases e outros corpos celestes causadas pela força gravitacional.↰
- Relatividade geral:
- teoria que prevê as leis da Física sendo aplicadas em todos os sistemas de referência que se movem, com velocidade constante ou acelerada, e também para campos gravitacionais, relacionando a gravidade às propriedades de espaço-tempo.↰
- Radiação:
- emissão de energia por meio de ondas ou de partículas.↰
Página 24
A evolução do Universo desde o Big Bang
De acordo com a teoria do Big Bang, cerca de 13,7 bilhões de anos atrás, todo o espaço, a energia e a matéria que conhecemos estavam concentrados em uma pequena região, com densidade e temperatura tendendo a infinito, a chamada singularidade. Em razão dessas condições, no início, somente a energia se manifestava e não havia matéria. Com a expansão e o resfriamento contínuo do Universo, formou-se a matéria que temos atualmente, com seus diversos componentes, como galáxias, estrelas e planetas.
O esquema a seguir representa, de forma simplificada, os eventos que ocorreram após o Big Bang, em uma sequência temporal.
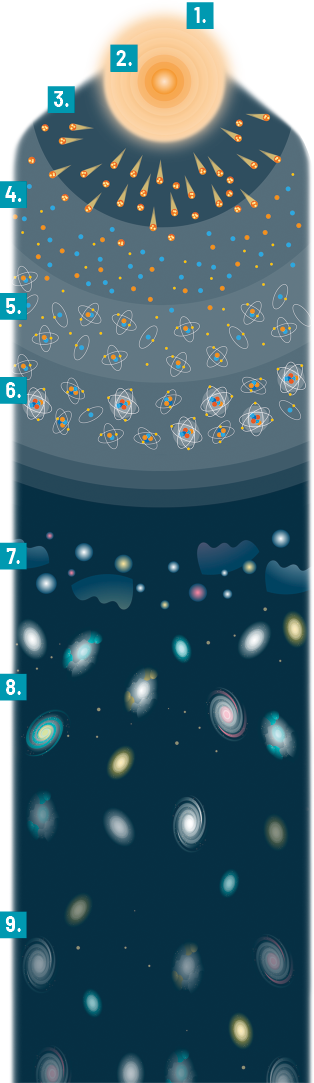
Imagem sem proporção e em cores fantasia.
1. 0 segundo: instante do Big Bang.
2. 10 elevado a menos 43 segundo: primeiro instante do qual conseguimos obter informações. Nesse momento, é possível diferenciar a interação gravitacional✚ das outras forças. Temperatura: 10 elevado a 32 Kelvin.
3. 10 elevado a menos 34 segundo: acontece a inflação, um período de curta duração no qual a taxa de expansão do Universo foi incrivelmente alta. O tamanho do Universo é multiplicado por um fator da ordem de 10 elevado a 30. Temperatura: 10 elevado a 27 Kelvin.
4. 1 segundo: nesse momento, o Universo é formado por prótons, nêutrons e elétrons espalhados em meio a fótons (partículas que compõem a luz) e outras partículas. Temperatura: 10 elevado a 10 Kelvin.
5. 3 minutos: acaba a formação dos núcleos atômicos dos elementos leves, como o hidrogênio, o hélio e o lítio. O Universo ficou repleto desses núcleos, que, com os elétrons, formavam um plasma✚. Temperatura: 10 elevado a 9 Kelvin.
6. 379.000 anos: a temperatura do Universo cai e os elétrons se estabilizam ao redor dos núcleos atômicos, formando átomos completos.
Com a formação dos átomos, a luz deixou de estar acoplada à matéria, o Universo se tornou transparente e uma grande quantidade de radiação foi liberada, formando a radiação cósmica de fundo que observamos até os dias atuais. Temperatura: 2.970 Kelvin.
7. 400 milhões de anos: ocorre a formação das primeiras estrelas, oriundas de nuvens de gases que se aglomeraram.
8. 500 milhões de anos: nesse período, foram originadas as primeiras galáxias. Temperatura: 20 Kelvin.
9. 13,7 bilhões de anos: estado atual do Universo. Estudos indicam que a formação do Sistema Solar se iniciou há aproximadamente 4,6 bilhões de anos, proveniente de um condensado de gás e poeira, e evoluiu até chegar ao que conhecemos atualmente. Temperatura: 2 vírgula 73 Kelvin.
Imagem elaborada com base em: UNIVERSIDADE FEDERAL DO RIO GRANDE DO SUL. O Big Bang. Disponível em: https://s.livro.pro/km8vml.
UNIVERSITY OF CALIFORNIA. Origin of the elements. Disponível em: https://s.livro.pro/nnarvm. Acessos em: 11 jul. 2024.
Página 25
Evolução estelar
Imagens desta página sem proporção e em cores fantasia.
Nos primeiros minutos logo após o Big Bang, o Universo era completamente diferente do atual. Em razão da sua expansão e do seu resfriamento contínuo, a matéria foi se formando, os átomos se organizando e originando as estruturas que compõem o Universo, como as estrelas.
1. O que você sabe sobre o nascimento de uma estrela?
Resposta pessoal.
Espera-se que os estudantes expressem seus conhecimentos prévios sobre o nascimento das estrelas. Anote na lousa as respostas mais convenientes para discuti-las durante a leitura do texto.
O nascimento de estrelas geralmente ocorre em nebulosas, regiões do espaço com densas nuvens de gás e poeira interestelar. Os modelos atuais sugerem que as estrelas nascem da concentração de matéria, por causa de perturbações na vizinhança das nebulosas e da ação de forças gravitacionais.
Durante esse processo, a atração gravitacional provoca o colapso gravitacional✚ de pequenas regiões de gás e poeira dentro da nebulosa, formando núcleos que podem se tornar estrelas. Esses núcleos podem sofrer um aumento de massa e de temperatura em razão da atração gravitacional. Quando a temperatura do núcleo chega a 10 milhões de graus Celsius, inicia-se a fusão termonuclear✚ do hidrogênio e a nova estrela passa a emitir energia.
Astro (dimensão) Nebulosa de Orion: aproximadamente 2 vírgula 27 vezes 10 elevado a 14 quilômetro de diâmetro.

A formação e a evolução das estrelas são processos contínuos, que podem levar milhões ou bilhões de anos para se completar, passando por diferentes etapas. A imagem a seguir representa a evolução estelar em razão da massa inicial, considerando como referência a massa do Sol abre parênteses M início subscrito, símbolo de um círculo com um ponto ao centro, fim subscrito é igual a 1 vírgula 99 vezes 10 elevado a 30 quilogramas fecha parênteses seguindo em ordem crescente de massas, de A até E.
A.

B.

C.

D.

E.

Representação da evolução estelar.
Imagens elaboradas com base em: COMINS, Neil F.; KAUFMANN III, William J. Descobrindo o Universo. 8. ed. Porto Alegre: Bookman, 2010. p. 424.
- Colapso gravitacional:
- concentração gradativa de matéria em regiões de maior densidade por causa da força gravitacional, diminuindo o volume da matéria e aumentando, de forma considerável, sua densidade.↰
- Fusão termonuclear:
- reação em que núcleos de átomos leves se combinam a altíssimas temperaturas para formar um único núcleo, mais pesado, ocorrendo grande liberação de energia.↰
Página 26
A cor, o tamanho, a massa e as linhas espectrais✚ são propriedades utilizadas para caracterizar as estrelas.
O núcleo das estrelas emite radiação em diversas faixas de frequência do espectro eletromagnético✚. Essa luz interage com os gases presentes nas camadas externas da estrela e algumas dessas faixas de frequência são absorvidas, dependendo da composição estelar. A análise das linhas espectrais permite saber os elementos químicos que constituem a estrela.
Ao estudar a abundância de elementos químicos por meio de linhas espectrais estelares, a astrônoma inglesa Cecilia Payne-Gaposchkin (1900-1979) concluiu que o hidrogênio e o hélio são os elementos predominantes do Sol e de outras estrelas. Antes de sua descoberta, acreditava-se que as estrelas eram compostas de elementos químicos semelhantes aos da crosta terrestre. Confira a seguir as linhas de absorção de luz que indicam a presença do elemento hidrogênio no Sol.

A classificação das estrelas usada atualmente tem como referência as linhas espectrais e foi estabelecida no início do século XIX pela astrônoma estadunidense Annie Jump Cannon (1863-1941) e pelos seus colegas do Harvard Observatory. Ela está ordenada de acordo com a temperatura da superfície estelar, utilizando as letras OBAFGKM. Confira a tabela apresentada.
| Classe espectral | Cor | Temperatura Kelvin |
|---|---|---|
|
O |
Azul-Violeta |
30.000-50.000 |
|
B |
Branca-Azul |
11.000-30.000 |
|
A |
Branca |
7.500-11.000 |
|
F |
Amarela-Branca |
5.900-7.500 |
|
G |
Amarela |
5.200-5.900 |
|
K |
Laranja |
3.900-5.200 |
|
M |
Vermelha-Laranja |
2.500-3.900 |
Fonte de pesquisa: COMINS, Neil F.; KAUFMANN III, William J. Descobrindo o Universo. 8. ed. Porto Alegre: Bookman, 2010. p. 350.
O Sol é uma estrela de tamanho e temperatura médios. De acordo com a classificação atual, pertence à classe espectral G, com temperatura chegando a aproximadamente 5.500 graus Celsius abre parênteses 5.773 Kelvin fecha parênteses em sua superfície. Assim como as demais estrelas, o Sol tem um ciclo evolutivo.
Imagem sem proporção e em cores fantasia.

Imagem elaborada com base em: COMINS, Neil F.; KAUFMANN III, William J. Descobrindo o Universo. 8. ed. Porto Alegre: Bookman, 2010. p. 424.
A. O acúmulo de matéria na região central de uma nuvem de gás e poeira aumenta a densidade e eleva a temperatura dessa região.
B. Quando o núcleo da protoestrela atinge cerca de 10 milhões de graus, começam as reações termonucleares, e o Sol passa a ser uma estrela propriamente dita, com diâmetro de 13 vírgula 9 vezes 10 elevado a 5 quilômetros. Essa é sua fase atual. Desde o início de sua vida até hoje, são estimados por volta de 4,6 bilhões de anos.
C. Daqui cerca de 5,5 bilhões de anos, o Sol será uma gigante vermelha. O hidrogênio do núcleo terá sido consumido e a estrela realizará fusão de hélio. Sua camada externa se expandirá, apresentando temperatura superficial aproximada de 3.500 Kelvin. Seu diâmetro aumentará em 100 vezes e seu brilho em 200 vezes.
D. O hélio do núcleo, quando for consumido, será transformado em carbono abre parênteses C fecha parênteses e oxigênio abre parênteses O fecha parênteses na camada externa ao núcleo. Nessa fase, a estrela se expandirá ainda mais, aumentando também sua luminosidade, e seu diâmetro chegará a aproximadamente 300 milhões de quilômetro. Sua temperatura estará próxima de 3.000 Kelvin.
E. Quando a estrela perde massa e o material de suas camadas externas é ejetado para o meio estelar, seu núcleo de carbono e oxigênio começa a ser exposto. Com tamanho equivalente ao da Terra e temperatura de 120.000 Kelvin, o núcleo brilhante ficará envolvido por poeira e gás em expansão.
F. O núcleo da nebulosa planetária remanescente do Sol se transformará em uma estrela anã branca. Sua composição será basicamente de carbono e oxigênio e seu tamanho será aproximadamente o do planeta Terra.
Página 27
Estrutura estelar e fonte de energia
De forma geral, as estrelas são corpos celestes esféricos constituídos predominantemente de hidrogênio e hélio em altas temperaturas, no estado de plasma. Elas têm como fonte de energia a fusão termonuclear.
2. Como você acha que o Sol emite luz?
Resposta pessoal. O objetivo da questão é verificar se os estudantes relacionam a luz visível emitida pelo Sol à radiação gerada pelas reações termonucleares que ocorrem em seu interior, como acontece em outras estrelas.
O Sol é classificado como uma estrela típica: nem muito grande, nem muito pequena; não muito fraca, tampouco muito brilhante. É uma fonte de energia indispensável para a vida na Terra. Existem bilhões de estrelas como o Sol na Via Láctea, por isso seu estudo serve como base de conhecimento sobre outras estrelas.
Considerando sua massa total, o Sol é composto de aproximadamente 70,6% de hidrogênio e 27,4% de hélio; o restante se divide entre oxigênio abre parênteses O fecha parênteses, carbono abre parênteses C fecha parênteses, nitrogênio abre parênteses N fecha parênteses, silício abre parênteses Si fecha parênteses, magnésio abre parênteses M g fecha parênteses, neônio abre parênteses N e fecha parênteses, ferro abre parênteses Fe fecha parênteses e enxofre abre parênteses S fecha parênteses. Sua massa é mantida unida por causa da atração gravitacional, produzindo imensa pressão e temperatura em seu núcleo. Além do núcleo, estudos evidenciam que o Sol possui mais cinco regiões que completam sua estrutura. Confira a seguir.
Imagem sem proporção e em cores fantasia.
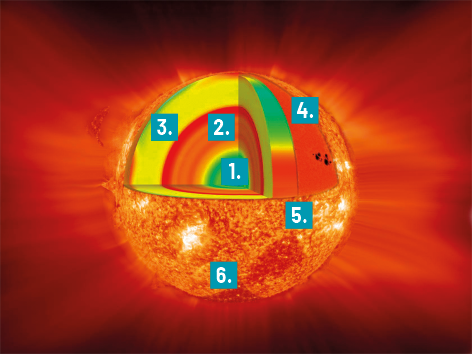
Imagem elaborada com base em: COMINS, Neil F.; KAUFMANN III, William J. Descobrindo o Universo. 8. ed. Porto Alegre: Bookman, 2010. p. 424.
1. Núcleo
Região onde ocorre a fusão termonuclear, que libera a energia que alimenta o Sol.
Nessa região, a temperatura chega a 15 milhões de graus Celsius e os átomos de hidrogênio se fundem para formar o átomo de hélio.
2. Zona radiativa
Camada pela qual a energia do núcleo é transportada para regiões mais externas pela radiação.
3. Zona convectiva
Região onde ocorre a convecção térmica, responsável pelo transporte de energia do núcleo até as camadas externas do Sol. Nessa região, a temperatura cai para 2 milhões de graus Celsius, e grandes bolhas de plasma se movem para a parte externa.
4. Fotosfera
É a camada visível do Sol, com temperatura de cerca de 5.500 graus Celsius e espessura de cerca de 500 quilômetros. Quando os gases do interior do Sol chegam à fotosfera, irradiam energia para fora em direção ao espaço. Vemos essa energia como luz visível e outras radiações eletromagnéticas.
5. Cromosfera
Camada logo acima da fotosfera. Ela é menos densa e brilhante do que a fotosfera, por isso não é facilmente visível. Durante os eclipses solares totais, quando a Lua cobre a fotosfera, a cromosfera pode ser vista como uma borda vermelha ao redor do Sol.
6. Coroa
Camada mais externa e rarefeita do Sol cuja temperatura aumenta com a altitude, chegando a 2 milhões de graus Celsius. Essa é a camada que pode ser mais bem observada durante os eclipses, formando uma coroa branca com numerosas tiras, que se estendem por milhões de quilômetros acima da superfície do Sol.
A explicação para a liberação de energia no núcleo das estrelas por meio de fusão termonuclear foi proposta pelo físico alemão Hans Albrecht Bethe (1906-2005) por volta de 1937. De acordo com Bethe, os elementos químicos se combinariam por meio de ciclos de reações que liberam energia, determinada pela diferença entre as massas dos núcleos reagentes e dos núcleos formados. No caso da fusão de hidrogênio em hélio, ao somar as massas dos núcleos de hidrogênio, encontra-se um valor maior do que a do núcleo do hélio que foi formado. Assim, uma pequena quantidade de massa é convertida na forma de energia. Essa reação pode ser representada por:
4 H subscrito 1 seta para a direita 1 H e subscrito 4 mais energia
Página 28
A quantidade de energia liberada nas reações termonucleares ocorridas no núcleo do Sol, por exemplo, pode ser obtida por meio da teoria da relatividade, formulada por Albert Einstein, que fornece uma relação entre matéria e energia pela equação:
E é igual a 'm' vezes c elevado ao quadrado em que: E é a energia; 'm' é a massa; e c elevado ao quadrado é a velocidade da luz ao quadrado.
ATIVIDADES RESOLVIDAS
R1. Calcule a energia liberada na reação termonuclear do hidrogênio para a formação de um núcleo de hélio. Para isso, considere:
- massa de 4 núcleos de hidrogênio: 'm' subscrito H é igual a 6 vírgula 68 vezes 10 elevado a menos 27 quilograma
- massa de 1 núcleo de hélio: 'm' subscrito H e é igual a 6 vírgula 65 vezes 10 elevado a menos 27 quilograma
Resolução
A diferença de massa abre parênteses delta 'm' fecha parênteses entre os reagentes e o produto é:
delta 'm' é igual a 'm' subscrito H menos 'm' subscrito He implica em delta 'm' é igual a 6 vírgula 68 vezes 10 elevado a menos 27 menos 6 vírgula 65 vezes 10 elevado a menos 27 portanto delta 'm' é igual a 0 vírgula 0 3 vezes 10 elevado a menos 27 quilograma.
Portanto, a energia liberada na reação é dada por:
E é igual a delta 'm' vezes c elevado ao quadrado implica em E é igual a 0 vírgula 0 3 vezes 10 elevado a menos 27 vezes abre parênteses 3 vezes 10 elevado a 8 fecha parênteses elevado ao quadrado portanto E é igual a 2 vírgula 7 vezes 10 elevado a menos 12 J ou E é igual a 2 vírgula 7 vezes 10 elevado a menos 12 W vezes s.
A luminosidade solar, que corresponde à energia total emitida pelo Sol por segundo, é aproximadamente 3 vírgula 8 vezes 10 elevado a 26 W. Assim, para produzir tal luminosidade, ele converte 600 milhões de toneladas de hidrogênio em hélio em seu núcleo por segundo. Essa taxa só é possível porque o Sol tem grande suprimento de hidrogênio, o bastante para continuar a mesma emissão de energia por outros 5 bilhões de anos.
Depois que todo o hidrogênio de seu núcleo for consumido, o Sol iniciará a fusão do hélio em carbono e em oxigênio, processo que também ocorre em outras estrelas.
Em estrelas com massas maiores do que 8 vezes M início subscrito, símbolo de um círculo com um ponto ao centro, fim subscrito, outros elementos mais pesados também são formados na fusão termonuclear.
Imagem sem proporção e em cores fantasia.
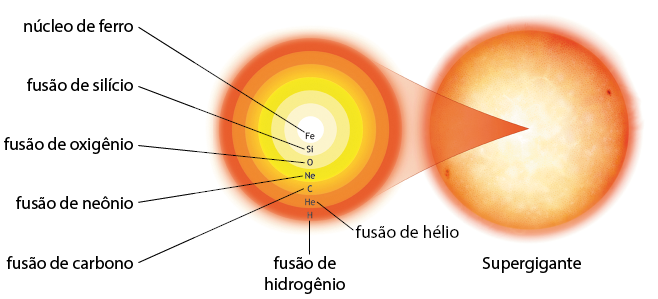
Imagem elaborada com base em: COMINS, Neil F.; KAUFMANN III, William J. Descobrindo o Universo. 8. ed. Porto Alegre: Bookman, 2010. p. 409.
Quando essas estrelas passam entre as fases Gigante e Supergigante, elas realizam fusão de hélio, carbono, oxigênio, neônio, magnésio e silício, até que seus núcleos se transformem em núcleos de ferro e o processo de fusão seja interrompido.
O estágio final para estrelas de grande massa é uma violenta explosão, conhecida como supernova, em que a maior parte de sua matéria é lançada para o espaço com velocidade muito alta, contribuindo para a distribuição de elementos químicos pelo Universo. Posteriormente, esse material ejetado pode formar novos corpos celestes, como planetas, asteroides e estrelas.
Astro (dimensão)
Supernova Cassiopeia A: aproximadamente 10 anos-luz de diâmetro.

Página 29
Formação dos buracos negros e supernovas
Astrônomos descobrem campos magnéticos em espiral nas bordas de buraco negro da Via Láctea
A nova imagem do buraco negro localizado no centro da Via Láctea revelou um campo magnético com uma estrutura muito semelhante à do que está situado no centro da galáxia M87, sugerindo que campos magnéticos intensos podem ser comuns a todos os buracos negros
ASTRÔNOMOS descobrem campos magnéticos em espiral nas bordas de buraco negro da Via Láctea. Jornal da USP, 29 mar. 2024. Disponível em: https://s.livro.pro/owxq84. Acesso em: 22 jul. 2024.
Em notícias e em diversos filmes de ficção científica, provavelmente você já ouviu falar em buracos negros. Na fotografia, podemos ver a região ao redor de um buraco negro.
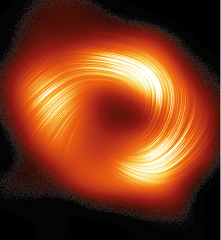
a ) O que você sabe sobre os buracos negros? Comente com os colegas.
Resposta pessoal. Eles podem citar que os buracos negros são o estágio final do ciclo da vida de estrelas de massa superior a 25 massas solares e que são corpos cujo campo gravitacional é muito intenso.
No interior das estrelas, após o início da fusão nuclear durante seu nascimento, há uma disputa entre a força gravitacional, que tenta comprimir toda a massa estelar, e a pressão interna gerada pela reação de fusão, que tenta expandir a estrela. Na juventude da estrela, quando há combustível para manter as fusões nucleares, o equilíbrio entre essas forças garante sua existência.
No fim da vida da estrela, faltam elementos químicos leves para manter as reações de fusão nuclear. Com isso, as forças internas desse corpo celeste se desequilibram, levando-a a um colapso.
Em uma estrela com massa acima de 8 vezes M início subscrito, símbolo de um círculo com um ponto ao centro, fim subscrito, quando falta combustível, a gravidade faz que ela se contraia rapidamente e exploda, liberando grande quantidade de energia. Essa explosão é conhecida como supernova.
As supernovas também podem surgir de sistemas binários de estrelas, nos quais uma estrela absorve massa da companheira e explode. Durante a explosão de uma supernova, ocorrem altos fluxos de nêutrons, que contribuem para a formação de elementos químicos mais pesados do que o ferro, como o zinco abre parênteses Z n fecha parênteses e o cobre abre parênteses C u fecha parênteses.
Parte da massa da estrela que passou pela fase de supernova é ejetada para o espaço. No entanto, outra parte dessa estrela pode se contrair, formando um núcleo pequeno, com grande massa, que pode evoluir em uma estrela de nêutrons ou em um buraco negro.
As estrelas de nêutrons se formam tendo como base estrelas com massa entre 8 e 25 vezes M início subscrito, símbolo de um círculo com um ponto ao centro, fim subscrito. Já os buracos negros se formam com a morte de estrelas com massas superiores a 25 vezes M início subscrito, símbolo de um círculo com um ponto ao centro, fim subscrito.
Astro (dimensão)
Pulsar de Vela: aproximadamente 20 quilômetros de diâmetro e localizada a cerca de 1.000 anos-luz da Terra.

b ) Que tipos de estrelas podem resultar em supernovas?
Resposta: As supernovas podem ocorrer em estrelas que têm massa superior a 8 massas solares. A observação desse fenômeno em outras galáxias é mais frequente, pois a presença de poeira estelar dificulta a observação de supernovas na Via Láctea.
c ) O Sol poderá se transformar em um buraco negro um dia? Explique sua resposta.
Resposta: Não. O Sol não tem a massa necessária para se transformar em um buraco negro. Estudos indicam que, futuramente, ele evoluirá para uma estrela classificada como anã branca.
d ) Qual é a importância dos estudos sobre as supernovas? Exponha suas opiniões para os colegas.
Resposta pessoal. Espera-se que os estudantes citem que o estudo de uma supernova auxilia na compreensão da origem e evolução do Universo e também de como se formam e se distribuem os elementos químicos nos corpos celestes.
Página 30
Formação de sistemas planetários
Agora, confira o trecho de reportagem a seguir.
Cientista brasileiro pode ter descoberto novo planeta no Sistema Solar
Possível planeta estaria localizado no chamado Cinturão de Kuiper
PIMENTEL, Carolina. Cientista brasileiro pode ter descoberto novo planeta no Sistema Solar. Agência Brasil, 22 fev. 2024. Disponível em: https://s.livro.pro/wysl2z. Acesso em: 22 jul. 2024.
3. Converse com um colega sobre o que vocês entendem por sistema planetário e citem o nome daquele a que o planeta Terra pertence.
Resposta pessoal. O objetivo desta questão é levar os estudantes a reconhecer o Sistema Solar como um sistema planetário e relacionar esse termo a um conjunto de planetas e outros astros não estelares que orbitam uma estrela.
A descoberta de novos sistemas planetários tem auxiliado a compreender como o Sistema Solar se formou. A explicação mais aceita atualmente indica que a origem dos sistemas planetários está ligada ao nascimento de estrelas provenientes de nuvens de gás e poeira interestelar, as nebulosas.
Estima-se que a formação do Sistema Solar teve início há cerca de 4,5 bilhões de anos, na Via Láctea, entre os braços de Sagitário e Perseu, quando uma nuvem de gás e poeira interestelar começou a se contrair e girar em torno de um centro, tornando-se cada vez mais densa, em razão da força gravitacional entre as partículas que compõem a nuvem.
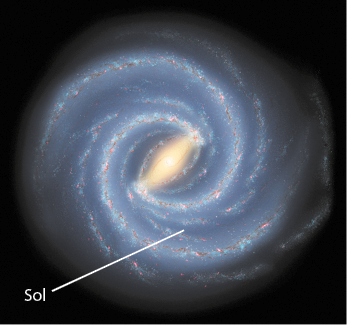
Com o passar do tempo, a massa de gás assumiu a forma de um disco, com uma região mais densa em seu centro, chamada de protossol, da qual se originou o Sol. Os planetas, satélites e outras estruturas se formaram a partir do material presente no disco.
A rotação das partículas da nebulosa teve grande importância na evolução do Sistema Solar, pois gerou um movimento que impediu o colapso das regiões mais exteriores ao protossol. As partes mais externas colapsaram na direção do centro mais lentamente, possibilitando, mais tarde, a formação dos planetas internos e externos. Confira o esquema a seguir.
Imagens desta página sem proporção e em cores fantasia.
A.

B.

C.

D.

E.

F.
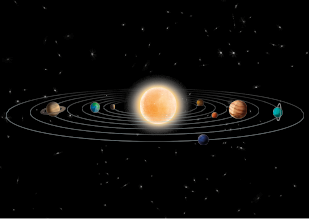
Representação da formação do Sistema Solar.
Imagens elaboradas com base em: COMINS, Neil F.; KAUFMANN III, William J. Descobrindo o Universo. 8. ed. Porto Alegre: Bookman, 2010. p. 154.
Página 31
A. No início da formação do Sistema Solar, uma nuvem de gás e poeira entra em lenta rotação e começa a se contrair.
B. Em virtude da força gravitacional, as partículas da nuvem se deslocam em torno de um centro, onde se acumulam, dando origem ao chamado protossol, que começa a crescer.
C. Outros corpos começam a se formar do material residual, que se concentrou na forma de um disco ao redor do protossol. Partículas de gelo e rocha colidem, iniciando a formação dos planetesimais✚.
D. Enquanto os planetas telúricos✚ acumulam matéria, o protossol torna-se quente o bastante para iniciar o processo de fusão termonuclear.
E. O vento solar varre para longe as partículas de gás e poeira, deixando apenas planetas, luas, asteroides, entre outros corpos.
F. Os planetas externos crescem por acúmulo de gás do disco externo, enquanto os planetas internos se aquecem, iniciando a diferenciação química.
Os planetas rochosos (Mercúrio, Vênus, Terra e Marte) se formaram mais lentamente, em regiões próximas do Sol, que são mais quentes e menos ricas em gases. O acúmulo de massa ocorreu, principalmente, por meio de colisões graduais entre planetesimais, que formaram corpos cada vez maiores, até darem origem aos satélites e planetas. Além das colisões, a gravidade contribuiu para o aumento de massa desses corpos.
Os planetas gasosos (Júpiter, Saturno, Urano e Netuno) se formaram mais rápido do que os rochosos, em um processo parecido com o da formação das estrelas. O crescimento rápido de suas massas e a força gravitacional atraiu matéria sólida e gases da região onde se formavam. Por estarem mais longe do Sol (uma região mais fria e rica em gases), apresentam composição gasosa.
Astro (dimensão)
Mercúrio: aproximadamente 4.879 quilômetros de diâmetro.
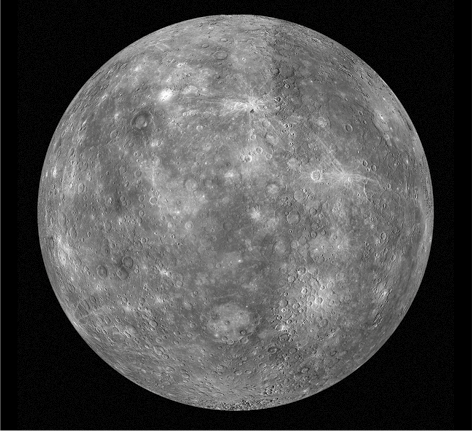
Astro (dimensão)
Netuno: aproximadamente 49.492 quilômetros de diâmetro.

Atualmente, são conhecidos mais de 5.000 sistemas planetários além do Sistema Solar, e mais de 8.000 planetas orbitando outras estrelas que não o Sol. A maioria desses planetas são gigantes gasosos, como Júpiter, e quase sempre são descobertos de modo indireto. Por exemplo, ao observarmos a luz emitida pelas estrelas que esses planetas orbitam, quando eles passam pela frente da estrela, há uma ligeira redução do brilho observado.
A descoberta de outros sistemas planetários aumenta a compreensão sobre a formação do Sol, da Terra e dos outros planetas, com base no estudo de sistemas mais jovens, mais antigos ou da mesma idade que o nosso.
Página 32
CONEXÕES com ... SOCIOLOGIA e FILOSOFIA
Origem do Universo em diferentes culturas
Ao longo da história da humanidade, compreender a origem do Universo tem sido uma tarefa que desperta o interesse do ser humano. Podemos perceber esse fato ao conhecer as diferentes explicações de diversas culturas sobre a origem do Universo e de alguns astros que o compõem.
Os mitos, por meio da Filosofia, são o princípio para reflexões a respeito de fenômenos da natureza e da existência das coisas, incluindo o ser humano e suas relações com o divino. Além disso, os mitos personalizam as crenças individuais e os sistemas culturais, influenciando estruturas sociais e identidades coletivas estudadas pela Sociologia.
Essas explicações influenciam a vida das pessoas, pois estão relacionadas a hábitos e crenças. Para muitos povos, a explicação para a origem do Universo estava no caos. É importante entender que a interpretação desses mitos deve ser feita levando em consideração a cultura a qual pertence, como menciona o físico brasileiro Marcelo Gleiser (1959 -) em seu livro A dança do Universo.
[...] mitos de determinadas culturas podem parecer completamente sem sentido em outras. De fato, um erro bastante comum é usarmos valores ou símbolos da nossa cultura na interpretação de mitos de outras culturas. Outro erro grave é interpretar um mito cientificamente, ou tentar prover mitos com um conteúdo científico. Os mitos têm que ser entendidos dentro do contexto cultural do qual fazem parte. [...]
GLEISER, Marcelo. A dança do Universo: dos mitos de criação ao Big Bang. São Paulo: Companhia das Letras, 2006. p. 20-21.
Vamos conhecer alguns mitos e lendas contados pelos povos.
Mitologia chinesa
No começo, só havia o caos, do qual surgiu Panku, primeiro ser com consciência.
Com um machado, ele dividiu o mundo entre o céu e terra. Ao morrer, seus olhos viraram o Sol e a Lua, o hálito se tornou vento e até os parasitas que viviam nele se transformaram nos animais que conhecemos.
SALI, Felipe. Como é a mitologia chinesa? In: O grande livro das mitologias. São Paulo: Abril, 2018. p. 64. (Coleção Mundo Estranho).
Imagem sem proporção e em cores fantasia.

Professor, professora: Na mitologia chinesa, o caos era como um ovo cósmico formado pelas energias primordiais yin e yang, e Panku teria nascido desse ovo cósmico
Página 33
Povos indígenas brasileiros
De acordo com a lenda indígena nheengatu, a origem do mundo teve como base a ação do ser sobrenatural Tupana.
No princípio, contam, havia só água, céu. Tudo era vazio, tudo noite grande. Um dia, contam, Tupana desceu de cima no meio de vento grande, quando já queria encostar na água saiu do fundo uma terra pequena, pisou nela. Nesse momento Sol apareceu no tronco do céu, Tupana olhou para ele. Quando Sol chegou no meio do céu seu calor rachou a pele de Tupana, a pele de Tupana começou logo a escorregar pelas pernas dele abaixo. Quando Sol ia desaparecer para o outro lado do céu a pele de Tupana caiu do corpo dele, estendeu-se por cima da água para já ficar terra grande.
No outro Sol [no dia seguinte] já havia terra, ainda não havia gente.
Quando Sol chegou no meio do céu Tupana pegou em uma mão cheia de terra, amassou-a bem, depois fez uma figura de gente, soprou-lhe no nariz, deixou no chão. Essa figura de gente começou a engatinhar, não comia, não chorava, rolava à toa pelo chão. Ela foi crescendo, ficou grande como Tupana, ainda não sabia falar.
Tupana, ao vê-lo já grande, soprou fumaça dentro da boca dele, então começou já querendo falar. No outro dia Tupana soprou também na boca dele, então, contam, ele falou. [...]
MARTINS, Roberto de Andrade. O Universo: teorias sobre sua origem e evolução. São Paulo: Moderna, 1994.

Imagem sem proporção e em cores fantasia.
Hinduísmo
Na religião hindu, o Universo é cíclico, com criação e destruição, representado pela dança rítmica do tempo e a natureza efêmera do deus Xiva:
[...]
Na noite do Brama (a essência de todas as coisas, a realidade absoluta, infinita e incompreensível), a Natureza é inerente e não pode dançar até que Xiva assim o deseje. O deus se alça de seu estupor e, através de sua dança, envia ondas pulsando com o som do despertar, e a matéria também dança, aparecendo gloriosamente à sua volta. Dançando, Ele sustenta seus infinitos fenômenos, e, quando o tempo se esgota, ainda dançando, Ele destrói todas as formas de nomes por meio do fogo e se põe de novo a descansar.
[...]
GLEISER, Marcelo. A dança do Universo: dos mitos de criação ao Big Bang. São Paulo: Companhia das Letras, 2006. p. 23-24.
a ) Como estudamos, a teoria do Big Bang é a mais aceita pelos cientistas. No entanto, conhecemos vários mitos de diferentes povos que tentam explicar a origem do Universo. Em sua opinião, qual é a importância desses mitos para esses povos?
Resposta pessoal. Espera-se que os estudantes respondam que os mitos contados fazem parte da identidade cultural dos diferentes povos e exercem acentuada influência na vida das pessoas, pois estão relacionados a muitos hábitos, valores e crenças.
b ) Junte-se a quatro colegas e pesquisem em livros e na internet outro mito a respeito da origem do Universo, dos astros ou de elementos da Terra. Em seguida, montem uma apresentação sobre esse mito e a importância dessa narrativa para os povos. Por fim, apresentem os resultados da pesquisa aos colegas da turma e à comunidade escolar.
Resposta pessoal. O objetivo desta questão é incentivar a autonomia dos estudantes ao realizar pesquisas, além de levá-los a conhecer outros mitos a respeito da origem do Universo e perceber a importância da valorização e do respeito à cultura dos diferentes povos.
Página 34
ATIVIDADES
1. De acordo com a teoria mais aceita entre os cientistas sobre a origem do Universo, julgue as afirmações a seguir como verdadeiras ou falsas, justificando as falsas.
a ) A teoria do Big Bang é a mais aceita pela comunidade científica para explicar a origem do Universo.
Resposta: Verdadeira.
b ) A teoria do Big Bang foi baseada, em parte, na teoria da relatividade de Albert Einstein e nos estudos do astrônomo Edwin Hubble.
Resposta: Verdadeira.
c ) O Universo não é estático e as galáxias estão se aproximando umas das outras, sugerindo que em algum período elas deveriam estar mais distantes.
Resposta: Falsa. Comentários nas Orientações para o professor.
2. A formação do Sistema Solar é um dos eventos de interesse da Cosmologia, envolvendo processos complexos que ocorreram há aproximadamente 4,6 bilhões de anos. De acordo com a teoria atualmente aceita sobre a formação do Sistema Solar, qual dos seguintes processos descreve melhor como nosso sistema planetário se originou?
a ) O Sistema Solar formou-se a partir da fusão de várias estrelas próximas, que eventualmente se consolidaram em um único sistema.
b ) Uma nuvem de gás e poeira interestelar começou a se contrair por causa da gravidade, formando um disco protoplanetário em torno de uma jovem estrela.
c ) Impactos catastróficos entre planetas já formados levaram à criação de corpos menores, como asteroides e cometas.
d ) A formação dos planetas foi um processo aleatório, influenciado principalmente pela radiação cósmica e eventos de supernova.
e ) O Sistema Solar surgiu em virtude de um processo de captura gravitacional de corpos celestes errantes na Via Láctea.
Resposta: Alternativa b.
3. Por muito tempo, a origem da energia irradiada pelo Sol era desconhecida. Atualmente, com o auxílio de teorias que explicam a evolução das estrelas, sabe-se que a energia solar provém de processos que ocorrem no interior dessa estrela, envolvendo núcleos de elementos leves. Que processo é esse? Explique como ele ocorre.
Astro (dimensão)
Sol: aproximadamente 1.390.000 quilômetros de diâmetro.

Resposta: Fusão termonuclear. A alta temperatura e a alta pressão no interior do Sol provocam a fusão de núcleos de hidrogênio, formando núcleos de hélio. Nesse processo, ocorre grande liberação de energia.
4. O ciclo de evolução das estrelas envolve diversas etapas que dependem de diferentes características das estrelas. Utilizando seus conhecimentos sobre o nascimento e a morte das estrelas, analise as afirmações a seguir.
I ) Os elementos químicos básicos de uma estrela são o hidrogênio abre parênteses H fecha parênteses e o hélio abre parênteses H e fecha parênteses.
II ) Acredita-se que o último estágio da vida do Sol seja na fase de anã vermelha.
III ) A explosão causada pela morte de uma estrela com massa maior do que 8 vezes a massa do Sol é chamada supernova.
IV ) A fusão termonuclear do hidrogênio se inicia no interior de uma estrela em formação quando seu núcleo atinge cerca de 10 milhões de graus Celsius.
Está correto o que se afirma em:
a ) apenas I.
b ) II e III.
c ) I e III.
d ) I, III e IV.
e ) todas as afirmativas.
Resposta: Alternativa d. No ciclo de evolução do Sol, acredita-se que, por conta de sua massa, seu último estágio seja na fase de anã branca.
5. Leia a manchete a seguir.
Cientistas resolvem mistério da Nebulosa de Anel Azul
Disponível em: https://s.livro.pro/izgtaw. Acesso em: 2 ago. 2024.
A manchete trata de um estudo para tentar entender a origem e a estrutura de uma nebulosa. Mas o que é uma nebulosa? Escreva em seu caderno a alternativa que responde corretamente a esta questão.
a ) São regiões com alta concentração de poeira interestelar e gases, nas quais pode haver o nascimento de estrelas.
b ) São corpos celestes iluminados, que orbitam os planetas e têm dimensões menores do que eles.
c ) São corpos celestes iluminados, sem luz própria, que refletem a luz de outras estrelas.
d ) São sistemas planetários, como o Sistema Solar, com apenas uma estrela central.
e ) São corpos celestes esféricos constituídos predominantemente por hidrogênio e hélio em altas temperaturas.
Resposta: Alternativa a.
Página 35
Professor, professora: Oriente os estudantes a resolver as questões de vestibular cujas alternativas são numeradas. Os valores das alternativas que respondem corretamente à questão devem ser somados, e a resposta é o resultado da somatória.
6. Nosso Sistema Solar é composto de uma estrela central, o Sol, e todos os corpos celestes que orbitam ao seu redor, incluindo planetas, asteroides, cometas e outros objetos menores. Os principais tipos de planetas no Sistema Solar são os rochosos e os gasosos. Além deles, astrônomos descobriram milhares de exoplanetas orbitando outras estrelas na Via Láctea.
Considerando o trecho citado anteriormente, assinale a alternativa ou as alternativas que correspondem corretamente à formação dos planetas do nosso Sistema Solar e exoplanetas.
01 ) Os planetas rochosos se formaram mais rapidamente do que os planetas gasosos.
02 ) A formação dos planetas rochosos ocorreu em regiões mais próximas do Sol.
04 ) Os planetas gasosos apresentam uma composição sólida por causa de sua formação rápida.
08 ) A maioria dos planetas fora do Sistema Solar são descobertos de forma direta, observando-se diretamente sua luz.
16 ) A descoberta de outros sistemas planetários ajuda a entender a formação do Sistema Solar.
Resposta: Soma: 01 mais 0 2 mais 16 é igual a 19.
7. Qual é a sequência correta que associa as informações dos dois quadros?
I. Satélite natural que gira ao redor da Terra.
II. Galáxia na qual está localizado o Sistema Solar com bilhões de outras estrelas.
III. Planeta que gira ao redor do Sol e ocupa a terceira posição em ordem de afastamento do astro.
IV. Conjunto de todos os astros, bem como de toda a matéria e todas as formas de energia existentes.
V. Conjunto formado por diversos planetas, satélites e cometas que giram ao redor do Sol.
A. Via Láctea.
B. Lua.
C. Sistema Solar.
D. Terra.
E. Universo.
Resposta: I − B; II − A; III − D; IV − E; V − C.
8. Diversos fenômenos ocorrem no Universo por causa da ação de forças gravitacionais. Essas forças, ao longo de bilhões de anos, transformaram nuvens de hidrogênio em grandes corpos estelares, nos quais ocorrem inúmeras colisões e reações de seus núcleos, liberando energia.
No Sol, cujo núcleo é composto principalmente de hidrogênio a altas temperaturas, há colisões com velocidades tão elevadas que ocorre a fusão termonuclear. A energia liberada nessas colisões no núcleo do Sol é a responsável por possibilitar o desenvolvimento de vida no planeta Terra.
a ) Sabe-se que a massa do núcleo de hidrogênio e de hélio é, respectivamente, 1 vírgula 67 vezes 10 elevado a menos 27 quilograma e 6 vírgula 65 vezes 10 elevado a menos 27 quilograma. Determine a diferença de massa resultante de uma reação de fusão de hidrogênio que ocorre no núcleo do Sol, caso em que quatro núcleos de hidrogênio se combinam para formar um núcleo de hélio. Considere que c é igual a 3 vírgula 0 0 vezes 10 elevado a 8 metro por segundo.
Resposta: 3 vírgula 0 0 vezes 10 elevado a menos 29 quilograma. Resolução nas Orientações para o professor.
b ) Considerando que as fusões ocorrem a uma taxa de 1 vírgula 5 vezes 10 elevado a 38 por segundo, determine a potência gerada no núcleo do Sol.
Dica
Para calcular a potência solar gerada, considere que ela corresponde à taxa (razão) da energia por unidade de tempo; nesse caso, de 1 segundo.
Resposta: 4 vezes 10 elevado a 26 W. Resolução nas Orientações para o professor.
9. Leia o trecho da obra Viagem ao céu, de Monteiro Lobato, que narra o diálogo entre o personagem Pedrinho e seu burro.
[...]
— E qual é a sua opinião, burro, sobre a formação da Lua? Há várias hipóteses.
— Sim. Uns sábios acham que a Lua foi um pedaço de Terra que se desprendeu no tempo em que a Terra ainda estava incandescente. Outros acham que o planeta Saturno foi vítima duma tremenda explosão causada pelo choque dum astro errante✚. Fragmentos de Saturno ficaram soltos no céu, atraídos por este ou aquele astro. Um dos fragmentos foi atraído pela Terra e ficou a girar ao seu redor.
[...]
LOBATO, Monteiro. Viagem ao céu. São Paulo: Brasiliense, 1970. v. 4. p. 214.
a ) Forme um grupo de 3 ou 4 integrantes e façam uma pesquisa referente a outras hipóteses de como ocorreu a formação da Lua, além das mencionadas no texto.
b ) Debatam e elejam a hipótese que o grupo julga mais adequada e elenquem argumentos que refutem as demais.
c ) Apresentem a hipótese escolhida e as ideias formuladas pelo grupo à turma.
Respostas nas Orientações para o professor.
- Errante:
- que anda sem destino certo.↰
Página 36
CAPÍTULO3
Os astros no Universo
Movimento dos astros
Algumas pessoas têm interesse em registrar astros do Universo por meio de fotografias. Essa tarefa exige experiência do fotógrafo, um local apropriado para registrar as imagens e o uso de algumas técnicas.
1. Analise a fotografia a seguir. O que as linhas pontilhadas curvas representam?

Resposta pessoal. O objetivo desta questão é levar os estudantes a perceber que as linhas curvas da fotografia representam o movimento dos astros no céu por causa do movimento de rotação da Terra.
Atividade(s) adaptada(s) acessível(is)
1. Em fotografias de longa exposição do céu noturno, é possível identificar rastros de luz das estrelas. Explique o que esses rastros representam.
Resposta: Espera-se que os estudantes respondam que os rastros de luz das estrelas representam o movimento aparente das estrelas no céu em razão do movimento de rotação da Terra.
Na fotografia da paisagem ficou registrado o movimento aparente de alguns astros no céu em uma noite com poucas nuvens, sem visibilidade da Lua, que é consequência do movimento de rotação da Terra em torno do próprio eixo.
Além da Terra, outros astros do Universo estão em constante movimento, até mesmo galáxias distantes, como verificado pelo astrônomo estadunidense Edwin Powell Hubble (1889-1953). Ao estudar a luz emitida pelas galáxias, ele percebeu que elas se afastam umas das outras e que, quanto maior a distância entre elas, maior a velocidade de afastamento.
Os corpos celestes que fazem parte do Sistema Solar também estão em constante movimento em relação ao Sol e ao centro da Via Láctea, por exemplo. Os planetas se movimentam ao redor do Sol e de si mesmos, com os satélites naturais orbitando ao seu redor.
O movimento de rotação da Terra, no qual o planeta gira em torno do próprio eixo, é responsável pelo ciclo dia-noite, que tem duração de 24 horas.
Dica
Com o professor e os colegas, providenciem um globo terrestre e uma lanterna e simulem a ocorrência dos dias e das noites. Para isso, em um local com pouca luminosidade (se for na sala de aula, apaguem as luzes), liguem a lanterna, posicionando-a em frente ao globo com o feixe de luz apontado para a sua superfície. Girem o globo lentamente e verifiquem os locais que recebem luz da lanterna diretamente (dia) e os que não recebem (noite).
Lembrem-se de que a Terra gira de oeste para leste.
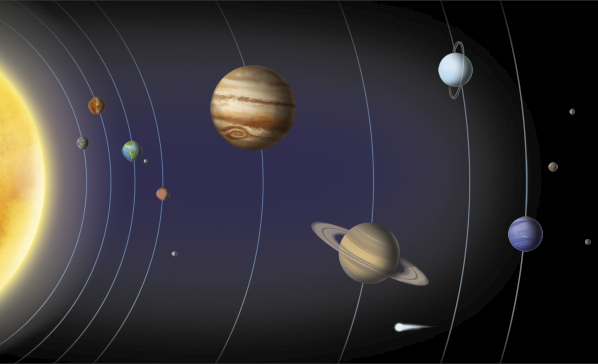
Já o movimento de revolução, em que a Terra descreve uma órbita elíptica em torno do Sol, ocorre em aproximadamente 365 dias e 6 horas e está relacionado à marcação dos anos.
O movimento de revolução da Terra em relação ao Sol e a inclinação de seu eixo em relação ao plano de sua órbita estão vinculados, entre outros fatores, à ocorrência das estações do ano.
Imagem sem proporção e em cores fantasia.
Página 37
Movimento e repouso
Imagens desta página sem proporção e em cores fantasia.
Leia a tirinha a seguir.

SCHULZ, Charles M. Minduim. O Estado de S. Paulo, 19 nov. 2019, caderno 2, p. 30.
2. Qual movimento da Terra pode ser associado ao nascer do Sol, citado na tirinha?
Resposta: Movimento de rotação.
3. De que maneira a personagem conseguiria perceber a movimentação da Terra em relação ao Sol?
Resposta pessoal. Os estudantes podem citar que a personagem deve acordar cedo e observar o movimento aparente do Sol no céu, que é resultado do movimento de rotação da Terra.
Você já estudou que a Terra e outros astros estão em movimento em relação ao Sol. Note que nessa frase descrevemos o movimento da Terra em relação a outro astro, no caso, o Sol.
Para verificar se um corpo está em movimento ou em repouso, bem como definir sua localização, é necessário adotar um sistema de referência, isto é, um referencial.
Confira as imagens apresentadas.


Como mencionado anteriormente, a definição de movimento está relacionada ao referencial. Portanto, adotando como referencial a árvore, é o automóvel que está em movimento. Isso se deve ao fato de o automóvel alterar sua posição com relação à árvore, afastando-se dela.
No entanto, caso o referencial seja um dos ocupantes do veículo, o que está em movimento, afastando-se dele próprio, é a árvore. Além disso, é correto afirmar que os dois ocupantes do mesmo veículo estão em repouso, já que a distância entre eles não se altera. Assim, pode-se dizer que eles estão em repouso um em relação ao outro e em relação ao veículo.
Portanto, um corpo em movimento é aquele que varia suas posições no decorrer do tempo em relação ao referencial adotado. Caso contrário, isto é, se o corpo mantém sua posição, dizemos que ele está em repouso.
Dica
Vetores são quantidades definidas por uma magnitude, uma direção e um sentido. Costumam ser representados por segmentos de reta orientados, com o comprimento indicando a magnitude. Confira a seguir.

A posição abre parênteses expressão com detalhe acima, início da expressão, 's', fim da expressão, início do detalhe acima, seta para a direita, fim do detalhe acima fecha parênteses de um corpo é uma grandeza vetorial cujo módulo indica a distância a que ele está em relação à origem abre parênteses 's' é igual a 0 fecha parênteses do sistema de referência escolhido.
A variação das posições de um móvel em relação a um referencial é denominada deslocamento, que é definido pela diferença entre sua posição final abre parênteses expressão com detalhe acima, início da expressão, 's', fim da expressão, início do detalhe acima, seta para a direita, fim do detalhe acima fecha parênteses e sua posição inicial abre parênteses expressão com detalhe acima, início da expressão, 's', fim da expressão, início do detalhe acima, seta para a direita, fim do detalhe acima subscrito 0 fecha parênteses. Isto é:
delta expressão com detalhe acima, início da expressão, 's', fim da expressão, início do detalhe acima, seta para a direita, fim do detalhe acima é igual a expressão com detalhe acima, início da expressão, 's', fim da expressão, início do detalhe acima, seta para a direita, fim do detalhe acima menos expressão com detalhe acima, início da expressão, 's', fim da expressão, início do detalhe acima, seta para a direita, fim do detalhe acima subscrito 0
Para movimentos unidimensionais, é possível escrever o deslocamento sem a notação vetorial da seguinte forma:
delta 's' é igual a 's' menos 's' subscrito 0
Nesse caso, o valor delta 's' equivale ao módulo do vetor deslocamento e o sinal, positivo ou negativo, indica o sentido do deslocamento, sendo positivo quando o movimento é a favor do sentido de crescimento das posições (progressivo) e negativo quando o movimento é contrário (retrógrado).
Página 38
Confira o esquema a seguir.
Imagem sem proporção e em cores fantasia.
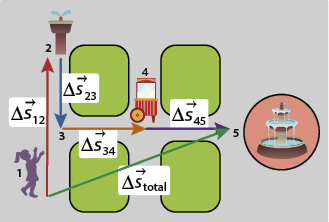
Júlia está passeando em um parque. Primeiro, ela vai a um bebedouro buscar água, saindo da posição 1 e indo para a posição 2, caminhando 10 metros. Depois, retorna para a posição 3, percorrendo 5 metros. Ela, então, vira para a esquerda e caminha 6 metros para chegar até um vendedor de pipoca, na posição 4. Por fim, caminha mais 6 metros para chegar até o chafariz, na posição 5.
Na imagem, cada segmento do trajeto de Júlia está representado pelos vetores deslocamento delta expressão com detalhe acima, início da expressão, 's', fim da expressão, início do detalhe acima, seta para a direita, fim do detalhe acima subscrito 12, delta expressão com detalhe acima, início da expressão, 's', fim da expressão, início do detalhe acima, seta para a direita, fim do detalhe acima subscrito 23, delta expressão com detalhe acima, início da expressão, 's', fim da expressão, início do detalhe acima, seta para a direita, fim do detalhe acima subscrito 34 e delta expressão com detalhe acima, início da expressão, 's', fim da expressão, início do detalhe acima, seta para a direita, fim do detalhe acima subscrito 45.
Como o deslocamento é resultado de uma operação vetorial, é possível analisar o deslocamento de Júlia em fragmentos e/ou total. Por exemplo, considerando o trajeto de 1 a 3, o deslocamento é dado pela seguinte relação.
delta expressão com detalhe acima, início da expressão, 's', fim da expressão, início do detalhe acima, seta para a direita, fim do detalhe acima subscrito 13 é igual a delta expressão com detalhe acima, início da expressão, 's', fim da expressão, início do detalhe acima, seta para a direita, fim do detalhe acima subscrito 12 mais delta expressão com detalhe acima, início da expressão, 's', fim da expressão, início do detalhe acima, seta para a direita, fim do detalhe acima subscrito 23

Como os dois vetores deslocamento são unidimensionais com sentidos opostos, consideramos um sentido com módulo positivo e outro negativo. Assim, podemos calcular o módulo do deslocamento entre os pontos 1 e 3 da seguinte forma.
delta 's' subscrito 13 é igual a delta 's' subscrito 12 menos delta 's' subscrito 23 implica em delta 's' subscrito 13 é igual a 10 menos 5 portanto delta 's' subscrito 13 é igual a 5 metros
Isto é, no trajeto de 1 a 3, o deslocamento de Júlia corresponde a 5 metros, vertical e para cima.
Analisando o trajeto de 3 a 5, há dois vetores unidimensionais com sentidos iguais. Portanto, o deslocamento nesse trecho abre parênteses delta expressão com detalhe acima, início da expressão, 's', fim da expressão, início do detalhe acima, seta para a direita, fim do detalhe acima subscrito 35 fecha parênteses pode ser obtido pela soma dos módulos dos vetores deslocamento da seguinte maneira.
delta expressão com detalhe acima, início da expressão, 's', fim da expressão, início do detalhe acima, seta para a direita, fim do detalhe acima subscrito 35 é igual a delta expressão com detalhe acima, início da expressão, 's', fim da expressão, início do detalhe acima, seta para a direita, fim do detalhe acima subscrito 34 mais delta expressão com detalhe acima, início da expressão, 's', fim da expressão, início do detalhe acima, seta para a direita, fim do detalhe acima subscrito 45 implica em delta 's' subscrito 35 é igual a delta 's' subscrito 34 mais delta 's' subscrito 45 implica em
implica em delta 's' subscrito 35 é igual a 6 mais 6 portanto delta 's' subscrito 35 é igual a 12 metros

Isto é, no trajeto de 3 a 5, o deslocamento de Júlia corresponde a 12 metros, horizontal e para a direita.
Por fim, considerando o trajeto total de Júlia (de 1 a 5), o deslocamento total abre parênteses delta expressão com detalhe acima, início da expressão, 's', fim da expressão, início do detalhe acima, seta para a direita, fim do detalhe acima subscrito total fecha parênteses é dado pela soma de dois vetores ortogonais, delta expressão com detalhe acima, início da expressão, 's', fim da expressão, início do detalhe acima, seta para a direita, fim do detalhe acima subscrito 13 é igual a 5 metros, vertical para cima, e delta expressão com detalhe acima, início da expressão, 's', fim da expressão, início do detalhe acima, seta para a direita, fim do detalhe acima subscrito 35 é igual a 12 metros, horizontal para a direita. Assim, podemos obter o módulo do vetor deslocamento total utilizando o Teorema de Pitágoras.
abre parênteses delta 's' subscrito total fecha parênteses elevado ao quadrado é igual a abre parênteses delta 's' subscrito 13 fecha parênteses elevado ao quadrado mais abre parênteses delta 's' subscrito 35 fecha parênteses elevado ao quadrado é igual a 5 elevado ao quadrado mais 12 elevado ao quadrado é igual a 169 portanto delta 's' subscrito total é igual a 13 metros

Isto é, no trajeto de 1 a 5, o deslocamento total de Júlia corresponde a 13 metros vírgula diagonal e para nordeste, como mostrado em verde na ilustração.
Página 39
É importante destacar que a distância percorrida abre parênteses d fecha parênteses no movimento de Júlia é diferente do módulo do deslocamento total abre parênteses, símbolo de barra vertical delta expressão com detalhe acima, início da expressão, 's', fim da expressão, início do detalhe acima, seta para a direita, fim do detalhe acima subscrito total, símbolo de barra vertical fecha parênteses, em que a distância percorrida é dada pela soma dos módulos dos vetores delta expressão com detalhe acima, início da expressão, 's', fim da expressão, início do detalhe acima, seta para a direita, fim do detalhe acima subscrito 12, delta expressão com detalhe acima, início da expressão, 's', fim da expressão, início do detalhe acima, seta para a direita, fim do detalhe acima subscrito 23, delta expressão com detalhe acima, início da expressão, 's', fim da expressão, início do detalhe acima, seta para a direita, fim do detalhe acima subscrito 34 e delta expressão com detalhe acima, início da expressão, 's', fim da expressão, início do detalhe acima, seta para a direita, fim do detalhe acima subscrito 45, isto é, d é igual a 10 mais 5 mais 6 mais 6 portanto d é igual a 27 metros.
No entanto, há situações em que a distância percorrida assume valor equivalente ao módulo do deslocamento, como em casos de movimentos retilíneos sem que haja inversão do sentido do movimento.
A associação da distância percorrida por um corpo ao tempo gasto no percurso nos dá a rapidez média, que pode ser determinada pela razão entre distância total percorrida e tempo decorrido, da seguinte maneira.
rapidez média é igual a início de fração, numerador: distância percorrida, denominador: intervalo de tempo, fim de fração
Dica
A conversão entre as unidades de medida da velocidade quilômetro por hora e metro por segundo pode ser realizada da seguinte maneira.

O fator 3,6 é devido ao fato de que 1 quilômetro é igual a 1.000 metros e 1 hora é igual a 3.600 segundos, de modo que:
1 quilômetro por hora é igual a 1.000 barra 3.600 metros por segundo
1 quilômetro por hora é igual a 1 barra 3 vírgula 6 metros por segundo
Por outro lado, quando são conhecidos tanto a rapidez quanto a direção e o sentido de um movimento, temos a definição da velocidade, considerando o intervalo de tempo gasto para que um corpo realize determinado deslocamento. A velocidade média abre parênteses expressão com detalhe acima, início da expressão, v, fim da expressão, início do detalhe acima, seta para a direita, fim do detalhe acima subscrito m fecha parênteses de um corpo é definida como a razão entre o deslocamento abre parênteses delta expressão com detalhe acima, início da expressão, 's', fim da expressão, início do detalhe acima, seta para a direita, fim do detalhe acima fecha parênteses e o intervalo de tempo abre parênteses delta 't' fecha parênteses:
expressão com detalhe acima, início da expressão, v, fim da expressão, início do detalhe acima, seta para a direita, fim do detalhe acima subscrito m é igual a início de fração, numerador: delta expressão com detalhe acima, início da expressão, 's', fim da expressão, início do detalhe acima, seta para a direita, fim do detalhe acima, denominador: delta 't', fim de fração implica em expressão com detalhe acima, início da expressão, v, fim da expressão, início do detalhe acima, seta para a direita, fim do detalhe acima subscrito m é igual a início de fração, numerador: expressão com detalhe acima, início da expressão, 's', fim da expressão, início do detalhe acima, seta para a direita, fim do detalhe acima menos expressão com detalhe acima, início da expressão, 's', fim da expressão, início do detalhe acima, seta para a direita, fim do detalhe acima subscrito 0, denominador: 't' menos 't' subscrito 0, fim de fração
No Sistema Internacional de Unidades (SI), os valores numéricos para a rapidez e para o módulo da velocidade são expressos na unidade de medida metros por segundo abre parênteses metro por segundo fecha parênteses. Entretanto, outras unidades podem ser utilizadas no dia a dia, como o quilômetro por hora abre parênteses quilômetro por hora fecha parênteses.
A rapidez em que um corpo se encontra em determinado instante de tempo é chamada de rapidez instantânea. Nos carros, ela é indicada no velocímetro.

Professor, professora: Comente com os estudantes que a rapidez instantânea indica o módulo da velocidade do corpo no instante de tempo considerado.
Nos movimentos retilíneos nos quais a orientação da velocidade e a rapidez são constantes, dizemos que o corpo se move em um movimento retilíneo uniforme ou MRU. Nesse caso específico, podemos desconsiderar as notações vetoriais e igualar a velocidade média à rapidez média do corpo, pois o módulo do deslocamento é igual ao valor da distância percorrida.
Da mesma forma que as variações das posições de um móvel em relação ao tempo permitem obter sua velocidade, as variações da velocidade durante determinado intervalo de tempo possibilitam obter a grandeza física aceleração, que pode atuar variando a rapidez do corpo, a orientação da velocidade ou ambas as propriedades do movimento.
Quando o módulo da velocidade de um corpo aumenta com o decorrer do tempo, o vetor aceleração atua a favor do vetor velocidade e o movimento é classificado como acelerado. Entretanto, quando o módulo da velocidade diminui com o decorrer do tempo, o vetor aceleração atua contrário ao vetor velocidade e o movimento é classificado como retardado.
Página 40
Imagens desta página sem proporção e em cores fantasia.




De modo geral, a aceleração média abre parênteses expressão com detalhe acima, início da expressão, a, fim da expressão, início do detalhe acima, seta para a direita, fim do detalhe acima subscrito m fecha parênteses é definida como a taxa de variação da velocidade, isto é, dependente apenas da velocidade inicial abre parênteses expressão com detalhe acima, início da expressão, v, fim da expressão, início do detalhe acima, seta para a direita, fim do detalhe acima subscrito 0 fecha parênteses e da velocidade final abre parênteses expressão com detalhe acima, início da expressão, v, fim da expressão, início do detalhe acima, seta para a direita, fim do detalhe acima fecha parênteses desenvolvidas por um corpo durante determinado intervalo de tempo. Assim, ela pode ser expressa como:
expressão com detalhe acima, início da expressão, a, fim da expressão, início do detalhe acima, seta para a direita, fim do detalhe acima subscrito m é igual a início de fração, numerador: delta expressão com detalhe acima, início da expressão, v, fim da expressão, início do detalhe acima, seta para a direita, fim do detalhe acima, denominador: delta 't', fim de fração implica em expressão com detalhe acima, início da expressão, a, fim da expressão, início do detalhe acima, seta para a direita, fim do detalhe acima subscrito m é igual a início de fração, numerador: expressão com detalhe acima, início da expressão, v, fim da expressão, início do detalhe acima, seta para a direita, fim do detalhe acima menos expressão com detalhe acima, início da expressão, v, fim da expressão, início do detalhe acima, seta para a direita, fim do detalhe acima subscrito 0, denominador: 't' menos 't' subscrito 0, fim de fração
A unidade padrão para a aceleração no Sistema Internacional de Unidades (SI) é o metro por segundo ao quadrado abre parênteses m barra s elevado ao quadrado fecha parênteses, mas outras unidades podem ser utilizadas, como o quilômetro por hora ao quadrado abre parênteses quilômetro por hora h elevado ao quadrado fecha parênteses.
Para movimentos retilíneos nos quais a aceleração tem mesma direção que a velocidade, a aceleração média pode ser escrita apenas como:
a subscrito m é igual a início de fração, numerador: delta v, denominador: delta 't', fim de fração implica em a subscrito m é igual a início de fração, numerador: v menos v subscrito 0, denominador: 't' menos 't' subscrito 0, fim de fração
ATIVIDADES RESOLVIDAS
R1. Considere um veículo andando em linha reta em uma via pública, com velocidade de 30 quilômetros por hora, quando o motorista avista o sinal vermelho e aciona o pedal do freio, parando em 5 segundos.
A aceleração média desse veículo pode ser obtida da seguinte forma:
Resolução:
a subscrito m é igual a início de fração, numerador: delta v, denominador: delta 't', fim de fração é igual a início de fração, numerador: v menos v subscrito 0, denominador: 't' menos 't' subscrito 0, fim de fração é igual a início de fração, numerador: 0 menos 30, denominador: 5 menos 0, fim de fração é igual a início de fração, numerador: menos 30, denominador: 5, fim de fração portanto a subscrito m é igual a menos 6 início de fração, numerador: k m, denominador: h vezes s, fim de fração é aproximadamente igual a menos 1 vírgula 7 metro por segundo quadrado
Dica
Nesse caso, a aceleração negativa indica que a velocidade do veículo diminui, logo o movimento é retardado.
R2. Agora, considere que, quando o semáforo mostra sinal verde, o motorista acelera seu veículo, movendo-se em linha reta e, após 4 segundos, o velocímetro marca 20 quilômetros por hora.
A aceleração média, dessa vez, é dada por:
Resolução:
a subscrito m é igual a início de fração, numerador: delta v, denominador: delta 't', fim de fração é igual a início de fração, numerador: v menos v subscrito 0, denominador: 't' menos 't' subscrito 0, fim de fração é igual a início de fração, numerador: 20 menos 0, denominador: 4 menos 0, fim de fração é igual a 20 sobre 4 portanto a subscrito m é igual a 5 início de fração, numerador: k m, denominador: h vezes s, fim de fração é aproximadamente igual a 1 vírgula 4 metro por segundo quadrado
Dica
Nesse caso, a aceleração positiva indica que a velocidade do veículo aumenta, logo o movimento é acelerado.
Página 41
ATIVIDADES
1. Um avião comercial realizou dois voos consecutivos, percorrendo trajetórias conforme mostram os vetores da figura a seguir.
Imagens desta página sem proporção e em cores fantasia.

Quais foram, respectivamente, a distância percorrida e o módulo do deslocamento desse avião nessa situação?
a ) 2.800 quilômetros e 2.800 quilômetros
b ) 2.800 quilômetros e 2.000 quilômetros
c ) 2.000 quilômetros e 2.000 quilômetros
d ) 1.600 quilômetros e 1.200 quilômetros
e ) 1.200 quilômetros e 1.600 quilômetros
Resposta: Alternativa b. Resolução nas Orientações para o professor.
2. Um automóvel se desloca por uma rua reta em que há dois radares usados para determinar a velocidade dos automóveis que trafegam por essa via. Ao passar pelo primeiro radar, o sistema de monitoramento dispara um cronômetro. Ao passar pelo segundo radar, o sistema para o cronômetro, medindo t é igual a 2 segundos.

Professor, professora: Oriente os estudantes a resolver as questões cujas alternativas são numeradas. Os valores das alternativas que respondem corretamente à questão devem ser somados, e a resposta é o resultado da somatória.
Assinale a(s) proposição(ões) CORRETA(S).
01 ) O sistema de monitoramento formado pelos dois radares mede a velocidade instantânea do automóvel.
02 ) O movimento pode ser classificado como progressivo.
04 ) Considerando a trajetória orientada no sentido da posição 's' subscrito 1 para 's' subscrito 2 e com os dados fornecidos pelo enunciado, é possível classificar o movimento como acelerado e progressivo.
08 ) Na posição 's' subscrito 1 é igual a 0, o cronômetro começa a marcação de tempo em 't' é igual a 1 segundo.
16 ) O módulo da velocidade média do automóvel registrada pelo sistema de monitoramento foi de 10 quilômetros por hora.
32 ) O módulo da velocidade média do automóvel registrada pelo sistema de monitoramento foi de 36 quilômetros por hora.
Resposta: Soma: 02 mais 32 é igual a 34. Comentários nas Orientações para o professor.
3. Um carro de corrida atinge a velocidade de 270 quilômetros por hora em uma reta. Para fazer a curva ao final dessa reta, o piloto deve diminuir a velocidade do carro para 72 quilômetros por hora em 5 segundos. Qual é aceleração média do carro nessa situação? Expresse o resultado em metro por segundo quadrado e classifique o movimento em acelerado ou retardado.
Resposta: menos 11 metros por segundo quadrado; retardado. Resolução nas Orientações para o professor.
4. Contemplando o planeta Marte sob o ponto de vista da Terra, é possível registrar, com fotografias, a seguinte trajetória percorrida no céu pelo planeta.

Esse movimento é conhecido como Marte retrógrado aparente e ocorre porque os planetas não orbitam o Sol com a mesma velocidade. Essa diferença de velocidade causa uma espécie de "ilusão de óptica", possibilitando o registro fotográfico. Sabendo que a trajetória é orientada para leste (da direita para a esquerda na fotografia), explique por que os termos retrógrado e aparente são usados.
Resposta: O termo retrógrado é utilizado, pois na região da imagem que parece um "laço" o planeta parece se deslocar no sentido oposto ao da orientação de sua trajetória. Já o termo aparente é usado, pois Marte não inverte o sentido de seu movimento, esse fenômeno observado ocorre por causa da diferença de velocidade com que a Terra e Marte orbitam o Sol, ou seja, o movimento somente aparenta ocorrer.
Página 42
Leis de Kepler
A observação do céu, em especial dos corpos celestes, é uma atividade que desde os tempos antigos desperta a curiosidade humana. O antigo monumento Stonehenge, localizado na Inglaterra, com cerca de 5.000 anos de existência, já era utilizado para observações astronômicas, além de seu uso para fins religiosos. Um pouco mais tarde, há aproximadamente cerca de 3.000 anos, os chineses já faziam observações de eclipses. Os gregos, há 2.500 anos, guiados pelas ideias do filósofo Anaximandro (610 a.C.-547 a.C.), propuseram modelos para explicar o movimento das estrelas sem usar mitologia. Desse modo, podemos ver como o movimento dos astros atraiu a atenção de diversos povos no decorrer da história.
Imagem sem proporção e em cores fantasia.

Todos esses estudos culminaram no desenvolvimento de modelos que explicassem o movimento dos corpos celestes que compõem o Sistema Solar. Nesse sentido, o cientista grego Cláudio Ptolomeu (90-168) elaborou o modelo geocêntrico, segundo o qual a Terra ficava no centro Sistema Solar, com os demais astros girando em órbitas ao seu redor. Esse modelo foi aceito por muitos séculos, até que estudos foram feitos pelo astrônomo polonês Nicolau Copérnico (1473-1543) e pelo cientista italiano Galileu Galilei (1564-1642), que propuseram o modelo correto para o Sistema Solar, o heliocêntrico, no qual o Sol está posicionado na região central, com os demais astros girando ao seu redor.
Desde então, diversos cientistas tentaram explicar o movimento dos astros do Sistema Solar. Entre esses estudiosos, destaca-se o astrônomo alemão Johannes Kepler (1571-1630).
Kepler fez descobertas importantes a respeito do movimento dos planetas. Até sua época, os modelos assumiam que os corpos celestes se moviam em composições de trajetórias circulares, o que não permitia reproduzir, de forma precisa, as posições dos planetas. Assim, durante muitos anos, o astrônomo alemão tentou encontrar um modelo que descrevesse de forma correta as órbitas dos planetas. Em 1605, ele concluiu que essas órbitas deveriam ser elípticas em torno do Sol, que estaria localizado em um dos focos da elipse. Essa teoria foi publicada em 1609 na obra A nova astronomia.
Em 1627, Kepler publicou um dos seus mais importantes trabalhos, as Tábuas rudolfinas, um catálogo de estrelas e tabelas planetárias produzido com base, principalmente, nas observações astronômicas feitas pelo seu orientador, o astrônomo dinamarquês Tycho Brahe (1546-1601). Apesar de todo o trabalho de Kepler com essas tabelas, elas se revelaram pouco eficientes, sendo revisadas e republicadas em 1650 no livro Urania propitia, escrito pela astrônoma e matemática polonesa Maria Cunitz (1607-1664). O livro de Cunitz forneceu tabelas com cálculos simplificados e atualizados que auxiliaram na divulgação da astronomia kepleriana.
As conclusões dos estudos de Kepler sobre os movimentos dos astros podem ser organizadas em três leis principais.

Página 43
Primeira lei de Kepler
A primeira lei de Kepler, ou lei das órbitas elípticas para o movimento planetário, define a trajetória descrita pelos planetas ao redor do Sol.
Todos os planetas se movem em órbitas elípticas ao redor do Sol, com o astro em um dos focos da elipse.
Imagens desta página sem proporção e em cores fantasia.
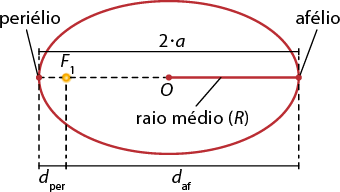
Como consequência desse movimento, a distância do Sol ao planeta varia ao longo de sua órbita. Quando o astro está mais próximo do Sol, ele se encontra em um ponto chamado periélio, e quando está mais distante esse ponto é chamado afélio.
A média aritmética entre as distâncias do afélio e do periélio representa a distância média do planeta ao Sol, chamada raio médio abre parênteses R fecha parênteses.
R é igual a início de fração, numerador: d subscrito per mais d subscrito a f, denominador: 2, fim de fração
Quando a Terra está no periélio, sua distância em relação ao Sol é de cerca de 147 vírgula 1 vezes 10 elevado a 6 quilômetro; já quando está no afélio, essa distância é de cerca de 151 vírgula 1 vezes 10 elevado a 6 quilômetro, resultando em um raio médio de aproximadamente 1 vírgula 5 vezes 10 elevado a 8 quilômetro (150 milhões de quilômetros). Tal valor define a unidade de comprimento chamada unidade astronômica abre parênteses, u a, fecha parênteses, muito utilizada em Astronomia.
1 unidade astronômica é igual a 1 vírgula 5 vezes 10 elevado a 8 quilômetro
PRÁTICA CIENTÍFICA
Construção de uma elipse
Por dentro do contexto
Quando um corpo celeste orbita outro, a distância relativa entre eles varia ao longo do período de revolução. Em alguns casos essa variação é grande, em outros é pequena.
a ) De que maneira podemos tentar observar como ocorre a variação da distância entre os corpos celestes no movimento orbital?
Resposta: Os estudantes podem citar que é possível construir modelos das órbitas dos corpos celestes, isto é, construir elipses a partir dos focos.
Materiais
- rolo de barbante
- dois alfinetes ou duas tachinhas
- metade de uma cartolina
- régua
- lápis
Como proceder
A. Trace uma linha reta de 30 centímetros na cartolina usando a régua. Nessa reta, faça marcações de 5 centímetros em 5 centímetros. Fixe os alfinetes em 5 centímetros e 25 centímetros. Esses dois pontos são os focos 'F' subscrito 1 e 'F' subscrito 2 da elipse. Amarre o barbante nos dois alfinetes deixando uma folga. Posicione o lápis no barbante, como mostra a figura a seguir.
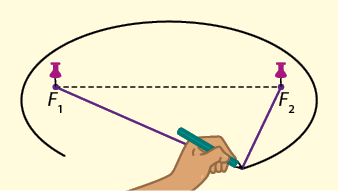
Atividade(s) adaptada(s) acessível(is)
A. Junte-se a um colega e, com a régua, tracem uma linha reta de 30 centímetros na cartolina. Nessa reta, façam marcações de 5 centímetros em 5 centímetros. Fixem os alfinetes em 5 centímetros e 25 centímetros. Esses dois pontos são os focos 'F' subscrito 1 e 'F' subscrito 2 da elipse. Amarrem o barbante nos dois alfinetes, deixando uma folga. Posicionem o lápis no barbante, puxando-o de modo que ele fique esticado.
B. Deslize a ponta do lápis sobre o papel para desenhar a elipse. Feito o primeiro desenho, desamarre o barbante dos alfinetes, coloque-os nas marcações de 6 centímetros e 19 centímetros e repita os procedimentos anteriores para desenhar uma nova elipse. Desenhe outras elipses mudando a posição dos focos para 7 centímetros e 18 centímetros, 8 centímetros e 17 centímetros, 9 centímetros e 16 centímetros, 10 centímetros e 15 centímetros.
Atividade(s) adaptada(s) acessível(is)
B. Deslizem a ponta do lápis sobre o papel para desenhar a elipse. Feito o primeiro desenho, desamarrem o barbante dos alfinetes, coloquem-nos nas marcações de 6 centímetros e 19 centímetros e repitam os procedimentos anteriores para desenhar uma nova elipse. Desenhem outras elipses mudando a posição dos focos para 7 centímetros e 18 centímetros, 8 centímetros e 17 centímetros, 9 centímetros e 16 centímetros, 10 centímetros e 15 centímetros.
C. Colem um barbante nas linhas das elipses desenhadas.
Orientação para acessibilidade
Professor, professora: Organize as duplas de modo que o estudante não vidente esteja acompanhado de um estudante vidente.
Análise
1. Conforme os focos se aproximam, a elipse assume qual formato?
Resposta: O objetivo desta questão é incentivar os estudantes a investigar e verificar como a distância entre os focos altera o formato da elipse. Eles devem responder que, à medida que os focos se aproximam, o formato da elipse se assemelha mais com o de uma circunferência.
Página 44
Segunda lei de Kepler
A segunda lei de Kepler, ou lei das áreas, está relacionada à velocidade dos planetas em órbita ao redor do Sol.
Uma linha imaginária que une o Sol e o planeta em órbita, denominada raio vetor, descreve áreas iguais em intervalos de tempo iguais.
A consequência mais importante dessa lei é que a velocidade orbital não é constante, variando de forma regular ao longo da trajetória descrita pelo planeta.
Imagens desta página sem proporção e em cores fantasia.
Como a trajetória dos planetas ao redor do Sol tem formato de elipse, com o astro maior em um dos focos, o raio vetor tem tamanho variável. Para A subscrito 1 é igual a A subscrito 2, os arcos percorridos pelo planeta em um mesmo intervalo de tempo abre parênteses delta 't' subscrito 1 é igual a delta 't' subscrito 2 fecha parênteses devem ser diferentes abre parênteses delta 's' subscrito 1 é maior do que delta 's' subscrito 2 fecha parênteses.
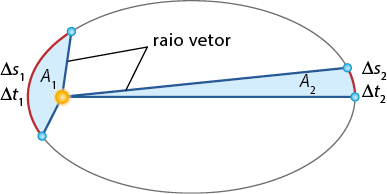
O movimento do planeta é acelerado quando se move do afélio ao periélio e retardado quando se move do periélio ao afélio. Assim, o módulo da velocidade dos planetas aumenta conforme eles se aproximam do Sol, mas diminui quando se afastam, rompendo com a teoria segundo a qual os movimentos celestes são uniformes. O vetor velocidade expressão com detalhe acima, início da expressão, v, fim da expressão, início do detalhe acima, seta para a direita, fim do detalhe acima configura-se tangente à trajetória elíptica.
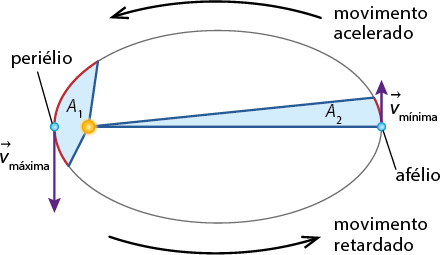
A variação no módulo da velocidade orbital foi explicada por volta de 1687, quando o cientista inglês Isaac Newton (1643-1727) publicou em sua obra Principia que uma força resultante, quando aplicada a um corpo com certa massa, gera aceleração, e que a força gravitacional surge da interação entre corpos em razão de suas massas. Esse assunto será detalhado ainda neste capítulo.
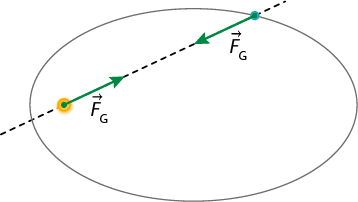
Dessa forma, a força que provoca uma aceleração no movimento do planeta é a força gravitacional entre o Sol e ele, que age na direção que passa pelo centro de massa✚ dos dois corpos, como mostrado na imagem apresentada.
- Centro de massa:
- ponto em uma distribuição de partículas ou corpos no qual é possível considerar que esteja concentrada toda a massa dessa distribuição.↰
Página 45
Terceira lei de Kepler
A terceira lei de Kepler, ou lei dos períodos, relaciona o tempo que o planeta leva para completar sua órbita, ou seja, seu período abre parênteses T fecha parênteses orbital, à distância média do planeta ao Sol, isto é, seu raio médio abre parênteses R fecha parênteses.
O quadrado do período da órbita de qualquer planeta abre parênteses T elevado ao quadrado fecha parênteses é diretamente proporcional ao cubo de sua distância média até o Sol abre parênteses R elevado ao cubo fecha parênteses.
início de fração, numerador: T elevado ao quadrado, denominador: R elevado ao cubo, fim de fração é igual a constante
Dica
Acesse o simulador de órbitas, disponível em: https://s.livro.pro/e8fkxs. Acesso em: 23 jul. 2024. Nele, você vai observar as órbitas da Terra e da Lua e poderá alterar controles para a massa da estrela e do planeta que a orbita.
Confira a seguir a medida aproximada do raio médio da órbita abre parênteses R fecha parênteses dos planetas do Sistema Solar em unidades astronômicas abre parênteses u a fecha parênteses, o período de suas órbitas abre parênteses T fecha parênteses em anos terrestres e o valor da razão início de fração, numerador: T elevado ao quadrado, denominador: R elevado ao cubo, fim de fração.
1. Mercúrio: R é igual a 0 vírgula 39 unidade astronômica, T é igual a 0 vírgula 24 ano e início de fração, numerador: T elevado ao quadrado, denominador: R elevado ao cubo, fim de fração é aproximadamente igual a 0 vírgula 97 ano elevado ao quadrado barra ua elevado ao cubo
2. Vênus: R é igual a 0 vírgula 72 unidade astronômica, T é igual a 0 vírgula 62 ano e início de fração, numerador: T elevado ao quadrado, denominador: R elevado ao cubo, fim de fração é aproximadamente igual a 1 vírgula 0 3 ano elevado ao quadrado barra ua elevado ao cubo
3. Terra: R é igual a 1 unidade astronômica, T é igual a 1 ano e início de fração, numerador: T elevado ao quadrado, denominador: R elevado ao cubo, fim de fração é igual a 1 ano elevado ao quadrado barra ua elevado ao cubo
4. Marte: R é igual a 1 vírgula 52 unidade astronômica, T é igual a 1 vírgula 88 ano e início de fração, numerador: T elevado ao quadrado, denominador: R elevado ao cubo, fim de fração é aproximadamente igual a 1 vírgula 0 1 ano elevado ao quadrado barra u a elevado ao cubo
5. Júpiter: R é igual a 5 vírgula 20 unidades astronômicas, T é igual a 11 vírgula 9 anos e início de fração, numerador: T elevado ao quadrado, denominador: R elevado ao cubo, fim de fração é aproximadamente igual a 1 vírgula 0 1 ano elevado ao quadrado barra u a elevado ao cubo
6. Saturno: R é igual a 9 vírgula 58 unidades astronômicas, T é igual a 29 vírgula 4 anos e início de fração, numerador: T elevado ao quadrado, denominador: R elevado ao cubo, fim de fração é aproximadamente igual a 0 vírgula 98 ano elevado ao quadrado barra u a elevado ao cubo
7. Urano: R é igual a 19 vírgula 20 unidades astronômicas, T é igual a 83 vírgula 7 anos e início de fração, numerador: T elevado ao quadrado, denominador: R elevado ao cubo, fim de fração é aproximadamente igual a 0 vírgula 99 ano elevado ao quadrado barra u a elevado ao cubo
8. Netuno: R é igual a 29 vírgula 97 unidades astronômicas, T é igual a 163 vírgula 7 anos e início de fração, numerador: T elevado ao quadrado, denominador: R elevado ao cubo, fim de fração é aproximadamente igual a 0 vírgula 99 ano elevado ao quadrado barra u a elevado ao cubo
Fonte de pesquisa: WILLIAMS, David R. Planetary Fact Sheet – Ratio to Earth Values. Nasa. Disponível em: https://s.livro.pro/9bm2lc. Acesso em: 23 jul. 2024.
4. Os valores mostrados anteriormente para a razão início de fração, numerador: T elevado ao quadrado, denominador: R elevado ao cubo, fim de fração, para os planetas do Sistema Solar, estão de acordo com a terceira lei de Kepler?
Resposta: Sim, estão de acordo. Como todos os valores apresentados para a razão início de fração, numerador: T elevado ao quadrado, denominador: R elevado ao cubo, fim de fração são aproximadamente 1, mantendo-se constante, podemos dizer que eles estão de acordo com a terceira lei de Kepler.
A terceira lei de Kepler permite determinar a distância média de qualquer planeta ao Sol, conhecendo seu período e a razão obtida por meio das informações relativas a outro planeta.
É possível concluir também que, quanto maior a distância média do planeta ao Sol, maior seu período orbital e mais lentamente ele se move. Assim, um planeta mais próximo do Sol tem a duração do ano mais curta do que aquele mais afastado.
Cabe ainda ressaltar que a terceira lei de Kepler não se aplica apenas aos planetas em órbita do Sol, mas também a qualquer corpo a orbitar outro em razão da influência de suas mútuas atrações gravitacionais quando o corpo central tem massa muito maior do que os demais corpos que o orbitam, como luas orbitando planetas e satélites artificiais orbitando a Terra.
Entretanto, algumas questões impediram os pensadores do século XVII de aceitar as leis de Kepler, como o fato de os planetas em órbita não atingirem repouso da mesma maneira que os objetos colocados em movimento na Terra. Essa explicação surgiu somente décadas depois, por volta de 1665, com os trabalhos de Newton.

5. A distância média de Júpiter ao Sol é aproximadamente 5,2 vezes a da Terra ao Sol. Qual é a duração do ano de Júpiter em anos terrestres?
Resposta: início de fração, numerador: T subscrito J início sobrescrito, 2, fim sobrescrito, denominador: R subscrito J início sobrescrito, 3, fim sobrescrito, fim de fração é igual a início de fração, numerador: T subscrito T início sobrescrito, 2, fim sobrescrito, denominador: R subscrito T início sobrescrito, 3, fim sobrescrito, fim de fração implica em início de fração, numerador: T subscrito J início sobrescrito, 2, fim sobrescrito, denominador: T subscrito T início sobrescrito, 2, fim sobrescrito, fim de fração é igual a início de fração, numerador: R subscrito J início sobrescrito, 3, fim sobrescrito, denominador: R subscrito T início sobrescrito, 3, fim sobrescrito, fim de fração implica em início de fração, numerador: T subscrito J início sobrescrito, 2, fim sobrescrito, denominador: 1 elevado ao quadrado, fim de fração é igual a início de fração, numerador: 5 vírgula 2 elevado ao cubo vezes R subscrito T início sobrescrito, 3, fim sobrescrito, denominador: R subscrito T início sobrescrito, 3, fim sobrescrito, fim de fração implica em T subscrito J é igual a início de raiz quadrada; 140 vírgula 608 fim de raiz quadrada portanto T subscrito J é aproximadamente igual a 11 vírgula 85 anos
Página 46
ATIVIDADES
Imagens desta página sem proporção e em cores fantasia.
1. Sabe-se que a distância entre o planeta Netuno e o Sol é bem maior do que a da Terra e o Sol. Com base nessa informação, responda às questões a seguir.
a ) O período de revolução de Netuno em torno do Sol é maior ou menor do que o da Terra? Justifique sua resposta.
Resposta: Maior. Sendo o raio de órbita de Netuno maior, de acordo com a terceira lei de Kepler, o período também será maior.
b ) Determine a razão entre os períodos de revolução de Netuno e da Terra, sabendo que os raios médios de suas órbitas são de aproximadamente 4 vírgula 5 vezes 10 elevado a 9 quilômetro e 1 vírgula 5 vezes 10 elevado a 8 quilômetro, respectivamente.
Resposta: Aproximadamente 164,3. Resolução nas Orientações para o professor.
c ) A velocidade orbital de Netuno é maior ou menor do que a da Terra? Justifique sua resposta.
Resposta: Menor. Como o raio médio da órbita de Netuno é maior do que o da Terra, sua velocidade orbital é menor.
2. O cometa Halley pôde ser visto da Terra, entre outras datas, nos anos de 1530, 1606, 1758, 1834, 1910 e 1986, e sua órbita está representada na imagem a seguir.
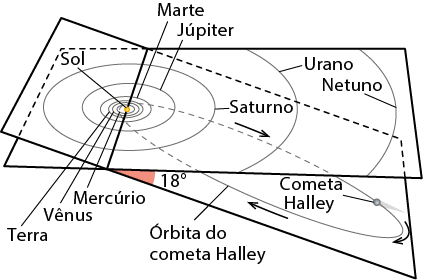
Determine o período orbital do cometa Halley e o ponto de sua trajetória em que há o maior módulo para sua velocidade. Justifique sua resposta.
Resposta: Possíveis resoluções: 1.606 menos 1.530 é igual a 76; 1.835 menos 1.758 é igual a 76; 1.986 menos 1.910 é igual a 76. Tem velocidade maior no periélio, ponto mais próximo do Sol.
3. A área total da elipse que corresponde à órbita da Terra em torno do Sol é de aproximadamente 7 vezes 10 elevado a 22 metros quadrados. Considerando que o intervalo de tempo gasto para a Terra percorrer os arcos arco A B, arco C D e arco E F é de 30 dias cada, responda às questões a seguir.
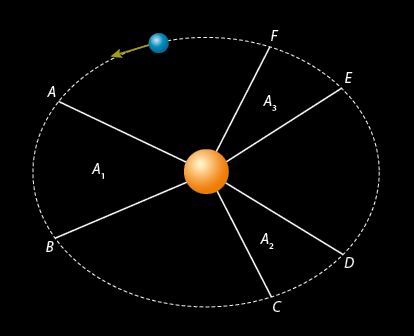
a ) Determine aproximadamente a soma das áreas A subscrito 1, A subscrito 2 e A subscrito 3.
Resposta: 1 vírgula 75 vezes 10 elevado a 22 metros quadrados. Resolução nas Orientações para o professor.
b ) Em qual(is) arco(s) a rapidez média da Terra é maior?
No arco arco A B a velocidade é maior do que nos arcos arco C D e arco E F.
c ) Considerando os arcos arco C D e arco E F, em qual deles a Terra realiza um movimento acelerado e em qual realiza um movimento retardado?
Resposta: A Terra realiza um movimento acelerado no arco arco E F e retardado no arco arco C D.
4. Após a órbita de Netuno, há uma região em formato de anel, composta de asteroides e outros corpos que remanesceram posteriormente à formação do Sistema Solar, chamada Cinturão de Kuiper. O início do cinturão está a uma distância de 30 unidades astronômicas do Sol e se estende até uma distância de 50 unidades astronômicas.

Imagine que todos os corpos dessa região se juntassem formando um planeta com centro de massa a cerca de 40 unidades astronômicas do Sol e que passasse a orbitá-lo. Qual seria a duração do ano desse planeta em anos terrestres sabendo que a distância média da Terra ao Sol é de 1 unidade astronômica?
Resposta: 64 anos. Resolução nas Orientações para o professor.
Página 47
CAPÍTULO4
Dinâmica do movimento dos corpos
Leis de Newton
Até aqui estudamos os movimentos dos astros sem nos preocuparmos com as suas causas, ou seja, sem considerarmos o que produziu ou modificou o movimento. A área da Física responsável por estudar as causas do movimento de um corpo e a ação de forças que agem nesse corpo é chamada de Dinâmica.
O filósofo grego Aristóteles (384 a.C.-322 a.C.) foi um dos primeiros pensadores a elaborar explicações envolvendo o conceito de força para explicar o movimento dos corpos. Mais tarde, com os experimentos realizados pelo cientista italiano Galileu Galilei (1564-1642), definiu-se que a tendência natural dos corpos, caso forças externas não estejam sendo aplicadas neles, é a de se manter em repouso ou em movimento. Desse modo, o movimento de um corpo poderia ocorrer mesmo sem estar sujeito à ação de uma força.
Mas a Dinâmica, como ramo da Física, foi de fato consolidada pelo físico inglês Isaac Newton (1643-1727), que desenvolveu as ideias a respeito do movimento propostas por Galilei e enunciou as leis fundamentais do movimento que atualmente levam o seu nome, as leis de Newton.

1. Você já ouviu falar em Isaac Newton? Conte para os colegas o que você sabe sobre ele.
Resposta pessoal. O objetivo desta questão é levar os estudantes a se expressarem, trocando informações prévias que tenham sobre Isaac Newton.
Isaac Newton revolucionou a Ciência ao encontrar provas físicas e matemáticas para corroborar a teoria heliocêntrica, que posicionava o Sol no centro do Sistema Solar. Newton baseou sua explicação para o movimento dos planetas e suas órbitas em três suposições físicas, chamadas leis fundamentais do movimento ou, simplesmente, leis de Newton.
De acordo com Newton, não só o movimento dos corpos na Terra, mas também o dos astros, é resultado da interação entre eles. Essa interação, chamada por Newton de força, é a grandeza física responsável por causar os movimentos e alterar suas características. De forma geral, a força surge da interação entre dois corpos, que podem estar em contato ou não.
Assim, a força é capaz de alterar o estado de movimento ou repouso de um corpo e sua aceleração. Confira a seguir alguns exemplos.


Dica
Em grego, força é dýnamis, palavra que deu origem ao termo Dinâmica, campo do conhecimento que trata dos movimentos relacionados a suas causas. Os princípios básicos da Dinâmica foram fornecidos, principalmente, por dois cientistas, o italiano Galileu Galilei e o inglês Isaac Newton. Por causa de Newton, a Dinâmica também é conhecida como Mecânica newtoniana.
2. Cite um exemplo de seu cotidiano em que uma força provoca um movimento ou altera as características dele.
Resposta pessoal. Os estudantes podem citar situações que envolvem empurrar algum objeto para que ele inicie um movimento ou mude a direção de seu movimento.
Página 48
A Mecânica newtoniana é aplicada na descrição dos movimentos, com algumas ressalvas. Primeiro, as três leis que serão tratadas neste capítulo são válidas em referenciais inerciais✚.
Além disso, a Mecânica newtoniana não é válida para situações que envolvam altas velocidades, por exemplo, próximas à velocidade da luz – nesses casos, é necessário aplicar conceitos da Teoria da Relatividade. Ela tampouco é válida para fenômenos em escala atômica – nesses casos, devemos usar conceitos da Mecânica Quântica.
A força e seus efeitos
3. Empurre, bem devagar, uma caneta sobre uma mesa. O que acontece com ela?
Resposta pessoal. O objetivo desta questão é levar os estudantes a identificar um dos efeitos de uma força, por exemplo, tirar um corpo do repouso ou provocar a variação de velocidade de um corpo.
Ao realizar a atividade anterior, você deve ter percebido que podemos identificar a força pelos efeitos que ela provoca sobre os corpos, como a variação da velocidade. Outro efeito que a força pode provocar é a deformação da estrutura do corpo.
4. Cite uma situação em que podemos perceber a deformação da estrutura de um corpo provocada por uma força.
Resposta pessoal. Os estudantes podem citar situações em que pressionaram algum objeto e este se deformou, por exemplo, uma lata de alumínio vazia ou uma garrafa de água vazia.
Variação da velocidade
Quando uma força é aplicada sobre um corpo, ela pode acelerá-lo ou desacelerá-lo, provocando a variação de sua velocidade. Na cena apresentada, do filme de ação Homem-Aranha 2, por exemplo, o personagem Peter Parker exerce uma força contrária ao movimento de um trem para colocá-lo em repouso.

5. Nessa situação, a força aplicada sobre o trem gerou uma aceleração positiva ou negativa? Justifique.
Resposta: Negativa. Espera-se que os estudantes respondam que a aceleração é negativa, pois foi contrária ao movimento do trem, diminuindo sua velocidade.
Da mesma forma, um veículo entra em movimento quando seus pneus aplicam força no solo.
Como a velocidade é uma grandeza vetorial, sua variação também está relacionada à mudança de direção e sentido, como ocorre em movimentos curvilíneos. Um exemplo disso é o que ocorre com os trens, que mantêm seu percurso porque os trilhos aplicam forças em suas rodas, permitindo-lhes fazer curvas.

6. Agora, analise a situação mostrada na fotografia. O que acontece com a velocidade da bola quando o goleiro a defende, impedindo o gol do adversário?
Resposta: A velocidade da bola varia em módulo, direção e sentido.
- Referenciais inerciais:
- referenciais em repouso ou em movimento retilíneo uniforme (quando o módulo da velocidade do corpo permanece constante) em relação a outro referencial inercial.↰
Página 49
Deformação
As forças aplicadas sobre um corpo podem provocar alterações em seu formato, como quando comprimimos uma mola ou amassamos uma lata de metal.
As deformações podem ser úteis, como no processo artesanal de esculpir um objeto de barro ou argila, em que o escultor aplica uma força para obter a forma desejada.

Dica
Valorize o artesanato de sua região. Procure saber se há feiras de artesanato em seu município e visite-as.
A natureza das interações
As forças estão em toda parte e podem surgir da interação entre corpos em contato (forças de contato) ou da interação à distância (forças de campo).
Todas as forças são descritas com base em quatro interações denominadas fundamentais: gravitacional, eletromagnética, forte e fraca.
A interação gravitacional, que é somente atrativa, ocorre em função da massa dos corpos: quanto maior a massa, maior a interação gravitacional. Quando soltamos um objeto próximo à superfície da Terra, a atração gravitacional é percebida pelo movimento do objeto em direção ao solo; já a atração entre dois lápis, por exemplo, é desprezível.
7. A interação gravitacional entre você e a Terra é definida como uma força de campo ou uma força de contato?
Resposta: Força de campo.
8. O que acontece quando atritamos uma caneta plástica no cabelo e a aproximamos de pequenos pedaços de papel? Essa situação tem relação com qual tipo de interação?
Resposta: A caneta atrai os pedaços de papel por meio da interação elétrica. Espera-se que os estudantes comentem que a caneta plástica vai adquirir cargas elétricas em excesso, passando a atrair pequenos pedaços de papel, e que isso é uma interação elétrica.
A interação eletromagnética ocorre por causa das propriedades elétricas e magnéticas da matéria. Apesar de terem sido estudadas separadamente por muito tempo, as forças elétricas e magnéticas atuam em conjunto, como nos trens do tipo maglev, que não têm rodas e se movimentam em trilhos que funcionam por meio da interação eletromagnética de ímãs com materiais supercondutores.

As interações chamadas de forte e fraca são relativas ao núcleo atômico e por isso recebem a denominação interações nucleares. Elas têm pequeno alcance, diferentemente das interações eletromagnéticas e gravitacionais, que agem a grandes distâncias.
A interação nuclear forte é a forma como as partículas que compõem os prótons e nêutrons interagem, sendo responsável por manter os núcleos dos átomos coesos. A interação nuclear fraca relaciona-se à radioatividade e à emissão de partículas pelos núcleos atômicos.
Independentemente de como a força age sobre os corpos e dos efeitos que ela produz, Newton organizou as conclusões de seus estudos em três leis.
Página 50
Primeira lei de Newton
Imagens desta página sem proporção e em cores fantasia.
A tendência dos corpos de se manterem em repouso ou em movimento é chamada de inércia e foi descrita na obra Princípios da filosofia, do matemático, físico e filósofo francês René Descartes (1596-1650). Essa ideia foi aprimorada por Newton, que escreveu em sua obra Principia: princípios matemáticos de filosofia natural – Livro I:
Lei I
Todo corpo continua em seu estado de repouso ou de movimento uniforme em uma linha reta, a menos que ele seja forçado a mudar aquele estado por forças imprimidas sobre ele.
[...]
NEWTON, Isaac. Principia: princípios matemáticos de filosofia natural – Livro I. 2. ed. São Paulo: Edusp, 2012. p. 53.
A afirmação anterior é conhecida como a primeira lei de Newton, ou princípio da inércia, válida para referenciais inerciais. Em termos da força resultante, ela pode ser interpretada da seguinte forma.
Todo corpo se mantém em repouso ou em movimento retilíneo uniforme (MRU) quando a força resultante que atua sobre ele é nula.
Dica
A força resultante é definida como a soma de todas as forças que atuam sobre um corpo. Se substituirmos as forças pela resultante, o efeito dessa ação sobre o corpo é a mesma.
Percebemos o princípio da inércia em um veículo que entra em movimento subitamente. Como nosso corpo tende a se manter em repouso, sentimos como se fôssemos lançados para trás. Se um veículo em movimento para subitamente, nosso corpo tende a se manter em movimento e sentimos como se fôssemos lançados para a frente. Por isso, devemos sempre utilizar o cinto de segurança, para evitar que nosso corpo continue o movimento quando o veículo freia ou para bruscamente.
Tanto em repouso quanto no MRU, a força resultante é nula e não há aceleração, o que podemos definir como estado de equilíbrio (equilíbrio estático em repouso e equilíbrio dinâmico no MRU). A primeira lei de Newton pode ser então compreendida como a tendência dos corpos a permanecer em equilíbrio, seja ele estático, seja dinâmico.
A.

A. Dizemos que um corpo está em equilíbrio estático abre parênteses símbolo de uma barra vertical expressão com detalhe acima, início da expressão, a, fim da expressão, início do detalhe acima, seta para a direita, fim do detalhe acima símbolo de uma barra vertical é igual a 0 fecha parênteses quando ele está em repouso abre parênteses símbolo de uma barra vertical expressão com detalhe acima, início da expressão, v, fim da expressão, início do detalhe acima, seta para a direita, fim do detalhe acima símbolo de uma barra vertical é igual a 0 fecha parênteses e a força resultante sobre ele é nula abre parênteses símbolo de uma barra vertical expressão com detalhe acima, início da expressão, 'F', fim da expressão, início do detalhe acima, seta para a direita, fim do detalhe acima subscrito R símbolo de uma barra vertical é igual a 0 fecha parênteses.
B.

B. Dizemos que um corpo está em equilíbrio dinâmico abre parênteses símbolo de uma barra vertical expressão com detalhe acima, início da expressão, a, fim da expressão, início do detalhe acima, seta para a direita, fim do detalhe acima símbolo de uma barra vertical é igual a 0 fecha parênteses quando ele está em movimento com velocidade constante abre parênteses símbolo de uma barra vertical expressão com detalhe acima, início da expressão, v, fim da expressão, início do detalhe acima, seta para a direita, fim do detalhe acima símbolo de uma barra vertical é diferente de 0 fecha parênteses e a força resultante sobre ele é nula abre parênteses símbolo de uma barra vertical expressão com detalhe acima, início da expressão, 'F', fim da expressão, início do detalhe acima, seta para a direita, fim do detalhe acima subscrito R símbolo de uma barra vertical é igual a 0 fecha parênteses.
Em relação ao movimento dos planetas, em razão do princípio da inércia, Newton concluiu que há uma força fazendo os planetas se manterem em órbitas elípticas em torno do Sol e que essa força é a gravidade.
Página 51
Segunda lei de Newton
A segunda lei de Newton descreve como uma força altera o movimento de um objeto, modificando sua velocidade, seja em módulo e/ou direção e sentido. Para a segunda lei, Newton escreveu em sua obra:
[...]
Lei II
A mudança de movimento é proporcional à força motora imprimida e é produzida na direção da linha reta na qual aquela força é imprimida.
[...]
NEWTON, Isaac. Principia: princípios matemáticos de filosofia natural – Livro I. 2. ed. São Paulo: Edusp, 2012. p. 54.
Newton utiliza o termo mudança de movimento para se referir à quantidade de movimento abre parênteses expressão com detalhe acima, início da expressão, Q, fim da expressão, início do detalhe acima, seta para a direita, fim do detalhe acima fecha parênteses, grandeza dada pelo produto entre a massa abre parênteses 'm' fecha parênteses de um corpo e sua velocidade abre parênteses expressão com detalhe acima, início da expressão, v, fim da expressão, início do detalhe acima, seta para a direita, fim do detalhe acima fecha parênteses, ou seja:
expressão com detalhe acima, início da expressão, Q, fim da expressão, início do detalhe acima, seta para a direita, fim do detalhe acima é igual a 'm' vezes expressão com detalhe acima, início da expressão, v, fim da expressão, início do detalhe acima, seta para a direita, fim do detalhe acima
Supondo que a massa de um corpo seja constante, então a mudança de movimento será a alteração da velocidade abre parênteses expressão com detalhe acima, início da expressão, v, fim da expressão, início do detalhe acima, seta para a direita, fim do detalhe acima fecha parênteses. A segunda lei destaca novamente a proporcionalidade direta entre força e aceleração e pode ser escrita como:
A força resultante que atua sobre um corpo é igual ao produto da sua massa pela aceleração adquirida. Essa aceleração apresenta a mesma direção e o mesmo sentido da força resultante que age sobre o corpo.
A segunda lei de Newton pode ser expressa em termos matemáticos da seguinte forma:
expressão com detalhe acima, início da expressão, 'F', fim da expressão, início do detalhe acima, seta para a direita, fim do detalhe acima subscrito R é igual a 'm' vezes expressão com detalhe acima, início da expressão, a, fim da expressão, início do detalhe acima, seta para a direita, fim do detalhe acima
No SI, massa abre parênteses 'm' fecha parênteses é expressa em quilograma quilograma, aceleração abre parênteses expressão com detalhe acima, início da expressão, a, fim da expressão, início do detalhe acima, seta para a direita, fim do detalhe acima fecha parênteses é expressa em metros por segundo ao quadrado abre parênteses metro por segundo quadrado fecha parênteses e força abre parênteses expressão com detalhe acima, início da expressão, 'F', fim da expressão, início do detalhe acima, seta para a direita, fim do detalhe acima subscrito R fecha parênteses, em newton abre parênteses N fecha parênteses. Uma força de intensidade 1 newton aplicada em um corpo de 1 quilograma produz uma aceleração de 1 metro por segundo quadrado na mesma direção e no mesmo sentido da força resultante aplicada sobre ele.
Dica
Quanto maior a força resultante sobre um objeto, maior será sua aceleração. Entretanto, um objeto de massa maior terá menor aceleração quando sujeito à mesma força aplicada a um objeto de menor massa.
Ao considerar as leis de Kepler e de Newton, pode-se explicar o movimento dos planetas em torno do Sol admitindo a hipótese de uma força dirigida deles para o astro, provocando uma aceleração que faz o vetor velocidade de cada planeta mudar de direção continuamente. Tal força dirigida ao Sol, que será definida neste capítulo, corresponde à gravidade.
Em particular, para a órbita elíptica de um planeta ao redor do Sol, como a da Terra, a velocidade é máxima no periélio e mínima no afélio, já que, pela segunda lei de Kepler, os planetas ganham velocidade quando se aproximam do Sol e perdem quando se afastam dele.
Imagem sem proporção e em cores fantasia.
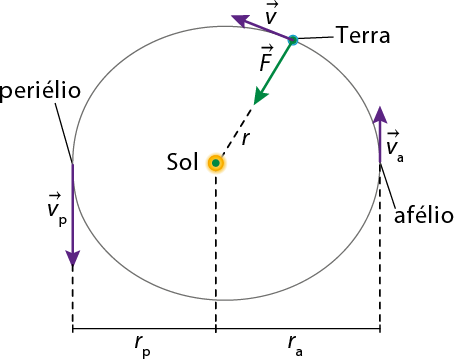
Página 52
Força resultante
Imagens desta página sem proporção e em cores fantasia.
A força é uma grandeza vetorial com intensidade, direção e sentido. Quando duas ou mais forças são aplicadas em um corpo, elas podem ser representadas pela força resultante abre parênteses expressão com detalhe acima, início da expressão, 'F', fim da expressão, início do detalhe acima, seta para a direita, fim do detalhe acima subscrito R fecha parênteses, determinada pela soma vetorial de todas as forças que agem sobre esse corpo. Ela equivale a uma força que, se atuasse sozinha, produziria o mesmo efeito que o conjunto de forças ao qual ele está submetido.
Observe a seguir como as forças se combinam para produzir a força resultante quando um conjunto de forças é aplicado sobre um corpo na mesma direção.
A.
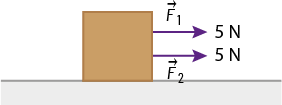
B.

Quando forças são aplicadas na mesma direção e no mesmo sentido (imagem A), a intensidade da força resultante é dada pela somatória dos módulos das forças aplicadas sobre o corpo (imagem B).
'F' subscrito R é igual a 'F' subscrito 1 mais 'F' subscrito 2
C.

D.

Quando forças são aplicadas na mesma direção, porém em sentidos diferentes (imagem C), a força resultante é dada pela diferença entre os módulos das forças aplicadas (imagem D).
'F' subscrito R é igual a 'F' subscrito 1 menos 'F' subscrito 2
E.

F.

De forma particular, se as forças aplicadas tiverem o mesmo módulo, mesma direção e forem aplicadas em sentidos opostos (imagem E), a força resultante sobre o corpo será nula (imagem F).
Representações de conjuntos de forças aplicadas em um corpo.
Agora, considere a situação ilustrada, em que um entregador puxa um conjunto de carrinho com uma caixa em cima aplicando uma força expressão com detalhe acima, início da expressão, 'F', fim da expressão, início do detalhe acima, seta para a direita, fim do detalhe acima subscrito E para deslocá-lo. Por causa da interação entre o conjunto do carrinho com caixa e a Terra, surge a força peso abre parênteses expressão com detalhe acima, início da expressão, 'F', fim da expressão, início do detalhe acima, seta para a direita, fim do detalhe acima subscrito P fecha parênteses, graças à atração gravitacional, e da interação com o solo surge uma força de sustentação, denominada força normal abre parênteses expressão com detalhe acima, início da expressão, 'F', fim da expressão, início do detalhe acima, seta para a direita, fim do detalhe acima subscrito N fecha parênteses, que será explicada mais adiante. No contato das rodas do carrinho com o solo, temos a força de atrito abre parênteses expressão com detalhe acima, início da expressão, 'F', fim da expressão, início do detalhe acima, seta para a direita, fim do detalhe acima subscrito a t fecha parênteses, que atua contra o movimento do conjunto, como uma resistência ao movimento.

Página 53
Considerando o conjunto carrinho e caixa como um ponto material, as forças podem ser representadas da maneira a seguir.
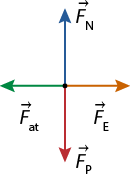
Analisando as forças separadamente, temos que a força peso abre parênteses expressão com detalhe acima, início da expressão, 'F', fim da expressão, início do detalhe acima, seta para a direita, fim do detalhe acima subscrito P fecha parênteses e a força normal abre parênteses expressão com detalhe acima, início da expressão, 'F', fim da expressão, início do detalhe acima, seta para a direita, fim do detalhe acima subscrito N fecha parênteses se anulam, pois têm o mesmo módulo, a mesma direção e sentidos opostos. A força de atrito abre parênteses expressão com detalhe acima, início da expressão, 'F', fim da expressão, início do detalhe acima, seta para a direita, fim do detalhe acima subscrito a t fecha parênteses se opõe à força aplicada pelo entregador abre parênteses expressão com detalhe acima, início da expressão, 'F', fim da expressão, início do detalhe acima, seta para a direita, fim do detalhe acima subscrito E fecha parênteses. Como têm a mesma direção, a mesma intensidade e sentidos opostos, essas forças também se anulam.
Portanto, se as forças internas são incapazes de alterar o estado de movimento do sistema e as forças externas geram uma força resultante nula, o conjunto carrinho e caixa não apresenta aceleração.
Uma força ou um conjunto de forças pode atuar em um corpo e gerar sobre ele uma aceleração que pode não só retirá-lo do repouso ou alterar o valor de sua velocidade, mas também alterar a direção e o sentido do movimento. Confira nas imagens a seguir exemplos que mostram o resultado da ação de forças aplicadas sobre os corpos.



Força peso
Observe as imagens a seguir.
Imagens desta página sem proporção.

Astros (dimensões)
Planeta Terra: aproximadamente 12.756 quilômetros de diâmetro.
Lua: aproximadamente 3.476 quilômetros de diâmetro.
9. O que existe de semelhante entre essas imagens? Troque ideias com os colegas.
Resposta pessoal. Os estudantes podem responder que, em ambas as situações, os corpos estão sujeitos à ação de uma força chamada gravidade.
Mesmo sem nos darmos conta, a gravidade atua sobre tudo o que está ao nosso redor. Ela é a força que nos mantém sentados em uma cadeira, faz os objetos caírem no chão quando os soltamos, ou seja, atrai todos os corpos em direção à Terra.
Página 54
Em seus estudos sobre movimento, Isaac Newton sugeriu que essa força que atrai os corpos em direção à superfície da Terra, impedindo-os de flutuar no espaço, também atua nos corpos celestes no Universo.
Os corpos na superfície da Terra e em suas proximidades estão sujeitos à força peso abre parênteses expressão com detalhe acima, início da expressão, 'F', fim da expressão, início do detalhe acima, seta para a direita, fim do detalhe acima subscrito P fecha parênteses, que nada mais é do que a força da gravidade associada a um corpo. A segunda lei de Newton permite calcular a intensidade dessa força. Considerando apenas a força gravitacional agindo sobre um corpo, este adquire uma aceleração de queda livre igual à aceleração da gravidade abre parênteses expressão com detalhe acima, início da expressão, 'g', fim da expressão, início do detalhe acima, seta para a direita, fim do detalhe acima fecha parênteses, assim:
expressão com detalhe acima, início da expressão, 'F', fim da expressão, início do detalhe acima, seta para a direita, fim do detalhe acima subscrito P é igual a 'm' vezes expressão com detalhe acima, início da expressão, 'g', fim da expressão, início do detalhe acima, seta para a direita, fim do detalhe acima
em que:
- 'F' subscrito P é a intensidade da força peso do corpo;
- 'm' é a massa do corpo;
- 'g' é o valor da aceleração da gravidade local.
Dica
A força peso entre um corpo e a Terra não deve ser confundida com a massa do corpo. Enquanto peso é uma força, medida em newton, a massa é a quantidade de matéria do corpo, medida em quilograma. A força peso depende da gravidade no local onde o corpo se encontra, enquanto sua massa é sempre a mesma, independentemente do local em que ele está.
Em regiões próximo à superfície terrestre, o valor da aceleração da gravidade é praticamente constante, com módulo aproximadamente igual a 9 vírgula 8 metros por segundo elevado ao quadrado, mas, para efeitos de cálculo, é comum aproximarmos esse valor para 10 metros por segundo elevado ao quadrado.
A direção e o sentido da força peso atuando em corpos próximo à superfície da Terra ou de outro astro celeste são vetoriais, têm direção passando pelo centro do astro em questão, e o sentido aponta para o centro desse astro.
Terceira lei de Newton ou princípio da ação e reação
10. Levante-se e caminhe pela sala. Após ficar em pé, o que você precisou fazer para caminhar?
Resposta: Empurrar o chão para trás com os pés.
Uma pessoa caminhando, sentada, deitada ou encostada em uma parede, por exemplo, pode interagir com algum corpo exercendo uma força sobre ele. Ao mesmo tempo, essa pessoa sente uma força com mesma intensidade e direção, mas no sentido oposto, sendo aplicada sobre ela.
Sobre as forças que surgem da interação entre corpos, Newton escreveu sua terceira lei:
[...]
Lei III
A toda ação há sempre oposta uma reação igual ou as ações mútuas de dois corpos sobre o outro são sempre iguais e dirigidas a partes opostas.
[...]
NEWTON, Isaac. Principia: princípios matemáticos de filosofia natural – Livro I. 2. ed. São Paulo: Edusp, 2012. p. 54.
A terceira lei de Newton pode ser interpretada da seguinte forma.
Se um corpo A exerce uma força em um corpo B abre parênteses expressão com detalhe acima, início da expressão, 'F', fim da expressão, início do detalhe acima, seta para a direita, fim do detalhe acima início subscrito, A B, fim subscrito fecha parênteses, o corpo B exerce uma força no corpo A abre parênteses expressão com detalhe acima, início da expressão, 'F', fim da expressão, início do detalhe acima, seta para a direita, fim do detalhe acima início subscrito, B A, fim subscrito fecha parênteses de mesma intensidade, mesma direção e sentido oposto abre parênteses expressão com detalhe acima, início da expressão, 'F', fim da expressão, início do detalhe acima, seta para a direita, fim do detalhe acima início subscrito, A B, fim subscrito é igual a menos expressão com detalhe acima, início da expressão, 'F', fim da expressão, início do detalhe acima, seta para a direita, fim do detalhe acima início subscrito, B A, fim subscrito fecha parênteses.
As forças de ação e reação surgem simultaneamente da interação entre dois corpos, de maneira que um recebe a ação e outro a reação. Essas duas forças têm mesma intensidade, mesma direção e sentidos opostos, mas não se anulam, pois atuam em corpos diferentes. Confira nas imagens a seguir alguns exemplos de interação entre corpos.
Página 55
Para caminhar, os pés empurram o solo para trás e o solo empurra os pés para frente com a mesma intensidade.

Para remar, os atletas aplicam uma força na água em um sentido, enquanto a água aplica uma força nos remos em sentido oposto.

O foguete expele os gases resultantes da queima de combustível aproximadamente na direção vertical e sentido para baixo e é empurrado por uma força de mesma intensidade, mesma direção, mas sentido contrário.

O funcionamento de aviões com hélices ou turbinas se baseia na interação com o ar. Tanto um equipamento como o outro lançam o ar para trás, enquanto o avião é impulsionado para a frente. A sustentação do avião também ocorre pela interação com o ar. Para subir, por exemplo, a aerodinâmica das asas é regulada para lançar ar para baixo, enquanto o avião é impulsionado para cima.
O princípio da ação e reação também é verificado nas interações a distância, como nas interações magnética, elétrica e gravitacional.
11. Você acha que um avião de hélice ou turbina funciona fora da atmosfera? Por quê?
Resposta: Não, pois fora da atmosfera não tem ar nem para proporcionar a sustentação do avião, nem propiciar a interação necessária para impulsioná-lo para a frente.
Em relação à órbita dos planetas, Newton concluiu que, como o Sol exerce uma força nos planetas para que eles possam manter seu movimento orbital, cada planeta também exerce uma força no Sol, que é igual e oposta àquela provocada por ele.
12. Na atração entre uma bola e a Terra, ambos os corpos sentem a força gravitacional; porém, quando a bola é abandonada próximo à superfície terrestre, observamos apenas a variação da velocidade da bola. Por quê?
Imagem sem proporção e em cores fantasia.
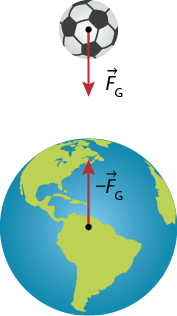
Resposta: A bola tem menor massa, praticamente desprezível quando comparada com a da Terra. Portanto, apesar de as forças serem de mesmo módulo, a bola é sujeita a maiores efeitos.
Página 56
Força normal
Imagens desta página sem proporção e cores fantasia.
13. O que acontece quando colocamos um livro sobre uma superfície macia, como uma almofada?
Resposta pessoal. Espera-se que os estudantes respondam que a almofada se deforma um pouco.
Ao soltarmos um livro no ar, a força peso entre a Terra e o livro faz que ele caia em direção ao solo. No entanto, quando colocamos esse mesmo livro sobre uma superfície macia, como uma almofada, a força peso continua agindo sobre ele, porém o livro fica em equilíbrio. Isso ocorre porque surge uma força do contato entre o livro e a almofada, de modo que a força resultante sobre ele é nula. Ela é chamada de força normal abre parênteses expressão com detalhe acima, início da expressão, 'F', fim da expressão, início do detalhe acima, seta para a direita, fim do detalhe acima subscrito N fecha parênteses e é sempre perpendicular à superfície. Nesse caso, ela pode ser percebida pela deformação da almofada.
Dica
Se o livro for colocado sobre qualquer superfície rígida, ela também se deformará, mesmo que seja de modo imperceptível, para sustentar o corpo sobre ela.
A força normal e a força peso não formam um par ação e reação. Se em um corpo agem duas forças, isso significa que ele está realizando duas interações diferentes. Da interação livro e Terra surge a força peso, com ação e reação agindo no livro e no planeta. Já da interação livro e mesa surge a força normal, com ação e reação agindo nos dois objetos. Confira na imagem a representação dessas forças de interação. Lembre-se de que o par de forças ação e reação sempre ocorre em dois corpos distintos.


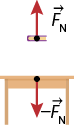
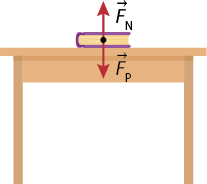
Para determinar a intensidade da força normal, é necessário analisar antes a forma como ocorre a interação entre o corpo e a superfície de apoio.
No exemplo anterior, como a superfície é horizontal e está em repouso em relação à Terra, a força peso e a força normal têm a mesma intensidade, de modo que a força resultante sobre o livro é nula e ele está em equilíbrio.
A igualdade da intensidade entre força peso e força normal não ocorre quando temos um objeto em repouso sobre um plano inclinado. No plano inclinado, a força peso e a força normal que atuam no corpo não têm a mesma direção, portanto elas não se anulam. Para analisar essa situação, pode-se realizar a decomposição das forças, adotando um plano cartesiano como referencial, de modo que o eixo das ordenadas (eixo y) seja perpendicular ao plano e o eixo das abscissas (eixo x) coincida com o plano inclinado, como ilustrado a seguir.
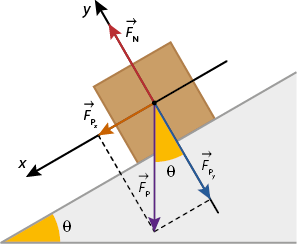
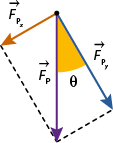
Página 57
Imagens desta página sem proporção e em cores fantasia.
Dica
Para compreender melhor como a força normal age em um livro sobre uma mesa, compare essa situação com uma mola comprimida. Se você já comprimiu uma mola, certamente percebeu que ela empurra sua mão para cima com a mesma força que você aplica para comprimi-la. Experimente fazer isso.
Como a força normal tem a direção do eixo das ordenadas, realizamos a decomposição da força peso em suas componentes expressão com detalhe acima, início da expressão, 'F', fim da expressão, início do detalhe acima, seta para a direita, fim do detalhe acima início subscrito, P subscrito x, fim subscrito e expressão com detalhe acima, início da expressão, 'F', fim da expressão, início do detalhe acima, seta para a direita, fim do detalhe acima início subscrito, P subscrito y, fim subscrito, dadas por:
'F' subscrito P subscrito x é igual a 'F' subscrito P vezes seno teta e 'F' início subscrito, P subscrito y, fim subscrito é igual a 'F' subscrito P vezes cosseno teta
Dessa forma, é possível verificar que um objeto desliza por um plano inclinado sem atrito graças à ação da componente expressão com detalhe acima, início da expressão, 'F', fim da expressão, início do detalhe acima, seta para a direita, fim do detalhe acima início subscrito, P subscrito x, fim subscrito da força peso. Já a intensidade da força normal é igual à intensidade da componente expressão com detalhe acima, início da expressão, 'F', fim da expressão, início do detalhe acima, seta para a direita, fim do detalhe acima início subscrito, P subscrito y, fim subscrito.
Força de tração
Cordas, fios ou cabos geralmente são usados para transmitir força. Quando uma corda é presa a um corpo e puxada ou tracionada, a força aplicada em um ponto da corda é transmitida por ela até o corpo. Essa é a força de tração expressão com detalhe acima, início da expressão, 'F', fim da expressão, início do detalhe acima, seta para a direita, fim do detalhe acima subscrito T, que atua sobre o corpo na direção da corda.
A força de tração também está presente em situações comuns de nosso cotidiano, como a utilização de cabos para a sustentação de luminárias. Observe a representação de um lustre com massa de 4 quilogramas pendurado no teto por uma corda ideal.
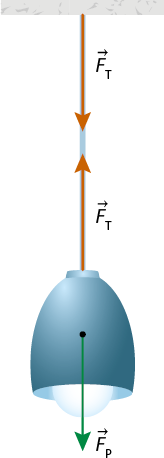
Como o lustre está em equilíbrio, a força resultante sobre ele é nula, ou seja, a força de tração na corda tem a mesma intensidade da força peso. Assim:
'F' subscrito R é igual a 'F' subscrito T menos 'F' subscrito P implica em 0 é igual a 'F' subscrito T menos 'F' subscrito P implica em 'F' subscrito T é igual a 'F' subscrito P implica em
implica em 'F' subscrito T é igual a 'm' vezes 'g' implica em 'F' subscrito T é igual a 4 vezes 10 portanto 'F' subscrito T é igual a 40 newtons
Como a corda exerce força de tração de mesma intensidade nas duas extremidades, a força de tração no teto também é de 40 newtons.
As cordas também podem ser utilizadas por meio de polias, que permitem alterar a intensidade, a direção e/ou o sentido de uma força. Uma polia ideal tem massa e atrito desprezíveis.
Polias estão presentes em quase todos os sistemas que utilizam cabos e correias para transmitir uma força, por exemplo, mastros de bandeiras, varais de roupas, persianas, equipamentos de ginástica, barcos e navios, motores, elevadores e guindastes.
As polias podem ser fixas ou móveis.
As polias fixas têm como função redirecionar a força, permitindo que seja aplicada na direção e no sentido desejados.
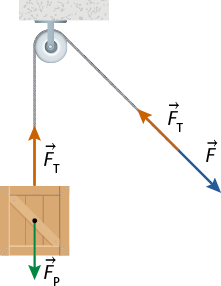
As polias móveis movimentam-se com a carga e têm a função de reduzir a intensidade da força necessária para sustentar o corpo.

Página 58
LIGADO NO TEMA
Segurança no trânsito
De acordo com um estudo divulgado pelo Ministério da Saúde, consolidado pelo Sistema de Informações sobre Mortalidade (SIM), no Brasil, em média, a cada hora pelo menos quatro pessoas morreram vítimas de acidente de trânsito no ano de 2022. Entre 2012 e 2022, a quantidade de óbitos envolvidos em acidentes de trânsito no país chegou a aproximadamente 410.000 pessoas.
A fim de diminuir a gravidade de lesões durante acidentes, as montadoras de veículos são obrigadas a inserir sistemas de segurança nos automóveis, como o cinto de segurança de três pontos, o airbag e os freios ABS.

O cinto de segurança de três pontos foi criado pelo engenheiro suíço Nils Bohlin (1920-2002), em 1959, e até hoje é considerado uma das invenções mais importantes da segurança de veículos. Antes disso, o cinto de segurança utilizado era preso apenas em dois pontos, não fixando o tórax ao banco, o que geralmente resultava em sérias lesões durante colisões em alta velocidade.
No Brasil, utilizar o cinto de segurança de três pontos é obrigatório e o seu uso reduz em até 45% o risco de morte para os passageiros da frente do carro e em até 75% para os passageiros do banco de trás. Mas muitos motoristas e passageiros ignoram a importância de sua utilização. De acordo com a Pesquisa Nacional de Saúde (PNS), realizada em 2019 e divulgada em 2021, 84,3% dos motoristas sempre utilizavam cinto de segurança; o índice para os passageiros da frente que sempre utilizavam o cinto é de 81,2%, porém, em relação aos ocupantes do banco traseiro, fica em apenas 54,6%.
O airbag, assim como os freios ABS, é outro item de segurança considerado obrigatório em todos os veículos fabricados no Brasil desde 2014.
O sistema do airbag tem sensores que detectam desacelerações bruscas, dando início a reações químicas com produção de gases que inflam uma bolsa. Isso diminui o impacto da pessoa em partes do automóvel, evitando ferimentos.
A bolsa do airbag infla rapidamente, em cerca de 30 m s (30 milésimos de segundo), e desinfla logo após encher, evitando a asfixia do motorista ou passageiro.
Imagem sem proporção e em cores fantasia.

De acordo com a primeira lei de Newton, ou princípio da inércia, em uma frenagem brusca os corpos dos ocupantes do veículo tendem a se manter em movimento, sendo lançados contra as peças do interior do veículo, o que pode causar fraturas e até a morte. O cinto de segurança impede que isso aconteça.
Página 59
Ao observar as imagens a seguir, note como os bonecos de teste, representando os integrantes do carro, continuam seu movimento por conta da inércia. As forças trocadas pelos integrantes com o veículo podem provocar danos ao corpo. O motorista, por exemplo, choca-se com o volante do carro, podendo ser projetado contra o para-brisa e lançado para fora do veículo, bem como o passageiro que ocupa o banco ao lado.
Já o ocupante do banco traseiro pode sofrer um impacto com o banco dianteiro, que por sua vez empurra o passageiro do banco logo à frente.
1.

2.

3.

Ao analisar as imagens a seguir, percebe-se que o cinto de segurança manteve o corpo dos ocupantes nos bancos, evitando que eles se chocassem violentamente com partes do carro. Nesse caso, uma imensa força, que é proporcional à variação de velocidade, é trocada entre o tórax da pessoa e o cinto. É por isso que em algumas situações as vítimas apresentam hematomas nas regiões do tórax e do abdome, causados pelo próprio cinto de segurança. O sistema airbag é ativado por sensores quando detecta um impacto e, associado ao cinto de segurança, ajuda na desaceleração dos integrantes do carro.
Se uma pessoa de 80 quilogramas estiver em um automóvel a 50 quilômetros por hora e houver uma colisão frontal, seu corpo será lançado para frente com uma força de intensidade equivalente ao peso de uma massa de 12 toneladas. Se usar o cinto de segurança, essa força reduz para o equivalente ao peso de uma massa de 2 toneladas.
1.

2.

3.

a ) Você usa cinto de segurança toda vez que utiliza um veículo, mesmo no assento traseiro? Caso sua resposta seja negativa, o que precisa melhorar?
Resposta pessoal. O objetivo desta questão é conduzir os estudantes a uma autoavaliação de seus hábitos e verificar se precisam alterá-los.
b ) Imagine-se como motorista de automóvel, quando percebe que um de seus passageiros não colocou o cinto de segurança. O que você deve fazer?
Resposta pessoal. Espera-se que os estudantes reconheçam que os motoristas são responsáveis pela segurança de todos os ocupantes de um automóvel e que devem orientar todos os passageiros para que usem o cinto de segurança.
c ) Um equipamento de segurança que ajuda na prevenção de lesões durante uma colisão na qual há crianças envolvidas é a cadeirinha. O que você sabe sobre esse dispositivo? Converse com seus colegas.

Resposta nas Orientações para o professor.
Página 60
ATIVIDADES
1. Considere que, a bordo de uma nave espacial que acaba de sair da atmosfera terrestre, um astronauta diz para a base de comando:
"Desligamos os foguetes, Isaac Newton nos dirige agora!"
De acordo com seus conhecimentos sobre as leis de Newton, explique o que o astronauta quis dizer com sua frase.
Resposta: Ao sair da atmosfera terrestre, mesmo sem a utilização de seus foguetes, a nave espacial permanece em movimento. Isso é possível em razão da primeira lei de Newton (lei da inércia), segundo a qual a velocidade é mantida, já que no espaço não existe forças de resistência para alterá-la.
2. Quando os comissários de bordo estão servindo comida aos passageiros de um avião, uma das primeiras medidas ao chegar ao local onde começarão a servir é travar as rodinhas do carrinho.

Por que os comissários de bordo tomam essa atitude? Qual lei de Newton se relaciona a essa situação?
Resposta: Os comissários travam as rodas do carrinho porque, a qualquer momento, o avião pode acelerar ou desacelerar durante o voo e, considerando o princípio da inércia, o carrinho poderia se movimentar e causar acidentes. É a primeira lei de Newton que se relaciona a essa situação.
3. Ao viajar de carro por estradas de terra após uma forte chuva, é comum o carro ficar atolado. Para desatolá-lo, também é comum outro carro rebocá-lo com um cabo, como mostra a fotografia a seguir.

Nessa situação, o que se pode dizer a respeito da intensidade da força que o carro sendo rebocado exerce sobre o carro à frente, e vice-versa?
Resposta: De acordo com o princípio da ação e reação, as forças têm mesma intensidade, mesma direção e sentidos opostos.
4. Os foguetes são veículos espaciais que lançam gases a alta velocidade para trás, por meio da combustão. Os foguetes se deslocam no sentido contrário ao lançamento dos gases, aumentando linearmente sua velocidade.
a ) Faça um diagrama reproduzindo um esboço do foguete e identifique as forças que atuam durante seu movimento. Não se esqueça de indicar a força peso, a força de resistência do ar, a força de ação e a força de reação.
Imagem sem proporção e em cores fantasia.

Resposta nas Orientações para o professor.
Atividade(s) adaptada(s) acessível(is)
a ) Descreva a direção e o sentido das forças que atuam em um foguete durante seu movimento de subida, na vertical para cima. Não se esqueça de indicar a força peso, a força de resistência do ar, a força de ação e a força de reação.
Resposta: Os estudantes devem citar que a força peso tem direção vertical e sentido para baixo; a força de resistência do ar tem direção vertical e sentido para baixo; a força de ação (força do foguete sobre os gases expelidos) tem direção vertical e sentido para baixo; e a força de reação (força dos gases expelidos sobre o foguete) tem direção vertical e sentido para cima.
b ) Considerando que a força da expulsão dos gases gerados na queima do combustível do foguete é a força de ação, de acordo com a terceira lei de Newton, qual é a força de reação? Explique.
Resposta: A queima dos combustíveis libera grande quantidade de gases, que são lançados para baixo. Pela lei da ação e reação, os gases lançados para baixo aplicam uma força no foguete para cima, fazendo-o subir.
c ) Se as forças que atuam sobre os gases e o foguete que se desloca são iguais, por que eles têm aceleração tão diferente? Explique.
Resposta: A diferença na aceleração se dá pela diferença da massa entre eles.
d ) Qual lei de Newton pode ser utilizada para explicar o fato descrito no item anterior? Justifique.
Resposta: Mantendo a força constante, a relação entre aceleração e massa é inversamente proporcional. Assim, quanto maior a massa, menor a aceleração, de acordo com a segunda lei de Newton.
5. Durante uma aula de Física, um estudante afirma que a soma de duas forças com módulos de 12 e 16 newtons sempre será 28 newtons. Uma colega da sala discorda dizendo que 28 newtons é apenas um dos valores possíveis para a soma dessas forças e que o resultado depende de outras informações além do módulo. Qual dos estudantes está argumentando corretamente? Justifique sua resposta utilizando a soma de vetores.
Resposta: A estudante que afirma que o resultado da soma das forças depende de outras informações além do módulo está correta, pois as forças podem estar em sentidos opostos ou fazendo um ângulo entre si, de forma que o resultado da soma seja diferente de 28 newtons.
6. Em uma partida de futebol, o jogador aplica uma força de 18 newtons na bola, que tem massa de 450 gramas. Qual é a aceleração adquirida pela bola?
Resposta: a é igual a 40 metros por segundo elevado ao quadrado. Resolução nas Orientações para o professor.
Página 61
Imagens desta página sem proporção e em cores fantasia.
7. Os pilotos de Fórmula 1 têm chamado a atenção por conta de seu treinamento físico para resistir aos desgastes sofridos ao longo das provas, principalmente o treinamento para fortalecimento do pescoço. Observando os pilotos, é possível perceber que eles têm o pescoço mais largo do que uma pessoa comum, isso porque as mudanças de velocidade, tanto nas retas quanto nas curvas, fazem que os pilotos sintam em sua cabeça acelerações que podem chegar a 5 vezes o valor da aceleração gravitacional abre parênteses 'g' é igual a 10 metros por segundo elevado ao quadrado fecha parênteses. Manter o pescoço fortalecido auxilia o piloto a evitar lesões ocasionadas pelo movimento da cabeça para frente, para trás e para os lados.
Suponha que um piloto de Fórmula 1 percorra de A para B o trecho de uma pista mostrada a seguir.
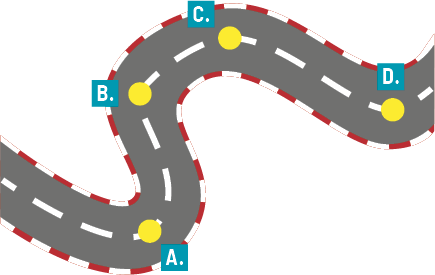
Para qual lado a cabeça do piloto é "jogada" em cada ponto considerando o sentido de movimento do carro na curva?
a ) A direita; B esquerda; 'C' esquerda; D direita.
b ) A direita; B direita; 'C' esquerda; D direita.
c ) A esquerda; B esquerda; 'C' esquerda; D direita.
d ) A direita; B esquerda; 'C' esquerda; D esquerda.
Resposta: Alternativa a.
8. Confira as três esferas a seguir, feitas com material sólido, dentro de um recipiente. Na situação mostrada, há somente as forças de contato entre as esferas e entre as esferas e as paredes do recipiente.
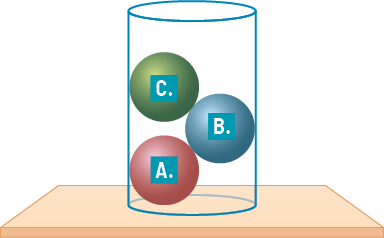
Quais são as forças que agem sobre a esfera B?
A.
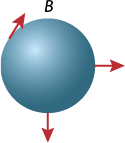
B.
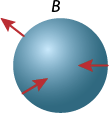
C.

D.
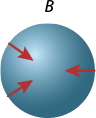
E.
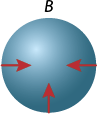
Resposta: Alternativa d.
9. Uma empresa de ônibus decidiu realizar um estudo para analisar as possibilidades de economizar combustível. Uma delas envolveu relacionar a força do motor com a aceleração e a massa total do ônibus em dois momentos distintos, como mostrado a seguir.


O ônibus com sua lotação máxima tem 20 toneladas e a ação da força expressão com detalhe acima, início da expressão, 'F', fim da expressão, início do detalhe acima, seta para a direita, fim do detalhe acima do motor produz uma aceleração de 5 metros por segundo quadrado. Sem passageiros, o ônibus tem 16 toneladas e é sujeito à ação da mesma força. Qual é a nova aceleração produzida?
Resposta: a é igual a 6 vírgula 25 metros por segundo elevado ao quadrado. Resolução nas Orientações para o professor.
10. Um guindaste precisa mover uma caixa do chão. Para isso, o operador do guindaste dá o comando para o braço mecânico começar a elevar a caixa. Ajustando para exercer uma força de 10.000 newtons, o operador percebe que a caixa não se move.

Sabendo que a caixa tem 7 toneladas, qual é o valor da intensidade da força normal na situação descrita? Considere g é igual a 10 metros por segundo elevado ao quadrado.
Resposta: 'F' subscrito N é igual a 60.000 newtons. Resolução nas Orientações para o professor.
Página 62
Lei da gravitação universal
Imagens desta página sem proporção e em cores fantasia.
A gravidade não é apenas uma força que atrai corpos para o centro da Terra, mas uma interação fundamental que existe entre qualquer corpo do Universo que tem massa. Essa força é mais intensa quanto maior for a massa dos corpos envolvidos e mais próximos eles estiverem. De forma geral, a força gravitacional de qualquer objeto age de forma a atrair outros objetos em direção a ele.
Por causa da abrangência universal dos fenômenos gravitacionais, a lei da gravidade de Newton ficou conhecida como lei da gravitação universal.
A força de atração gravitacional age em ambos os corpos envolvidos, formando um par de forças ação e reação orientadas ao longo da reta que passa pelo centro de massa desses dois corpos.
De acordo com a segunda lei de Newton, o efeito de uma força resultante aplicada em uma massa é a aceleração abre parênteses expressão com detalhe acima, início da expressão, 'F', fim da expressão, início do detalhe acima, seta para a direita, fim do detalhe acima subscrito R é igual a 'm' vezes expressão com detalhe acima, início da expressão, a, fim da expressão, início do detalhe acima, seta para a direita, fim do detalhe acima fecha parênteses, que pode estar relacionada com a variação do módulo da velocidade e/ou de sua orientação, o que dependerá da configuração entre os vetores força e velocidade, ou seja, se estão na mesma direção ou em direções diferentes, por exemplo. Confira as imagens a seguir.
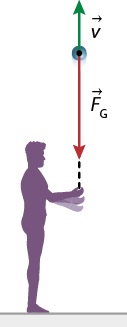
Um objeto lançado verticalmente para cima tem velocidade inicial na mesma direção da força de atração gravitacional. A intensidade de sua velocidade varia graças à existência de uma aceleração na mesma direção da velocidade.
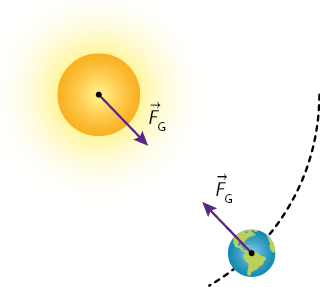
A velocidade de um planeta em órbita aproximadamente circular é praticamente perpendicular à força de atração gravitacional. A orientação da velocidade varia, enquanto sua intensidade se mantém constante, por causa da existência de uma aceleração com direção radial apontando para o centro da trajetória.
Assim, as forças que agem no movimento de queda dos corpos próximo à Terra e no movimento de corpos celestes em órbita são de mesma natureza gravitacional.
Segundo a lei da gravitação de Newton, se dois objetos têm massas M e 'm' e estão separados por uma distância d, a força gravitacional abre parênteses expressão com detalhe acima, início da expressão, 'F', fim da expressão, início do detalhe acima, seta para a direita, fim do detalhe acima subscrito G fecha parênteses entre eles é dada por:
'F' subscrito G é igual a início de fração, numerador: G vezes M vezes 'm', denominador: d elevado ao quadrado, fim de fração
Quanto maiores as massas, maior será a força de atração entre os corpos, e quanto maior for a distância entre eles, mais fraca será a força de atração.
Dica
Quando Newton propôs essa definição para a intensidade da força gravitacional, o valor da constante gravitacional e o da massa da Terra ainda não haviam sido determinados, de modo que ele considerava o produto desses dois fatores.
Página 63
Imagens desta página sem proporção e em cores fantasia.
Na relação apresentada na página anterior, G é uma constante de proporcionalidade, conhecida como constante gravitacional, e seu valor é de 6 vírgula 67 vezes 10 elevado a menos 11 N vezes m elevado ao quadrado barra quilogramas elevado ao quadrado.
A constante gravitacional foi medida pela primeira vez em 1798, pelo físico e químico francês Henry Cavendish (1731-1810).
Cavendish desejava estimar a densidade da Terra, mas para isso teria de estimar a massa do planeta. Ele mediu a força gravitacional entre duas pequenas esferas de chumbo presas às pontas de uma haste de madeira, que interagia com duas esferas maiores de chumbo, conforme modelo mostrado.
A força gravitacional entre as esferas, por menor que fosse, fez que elas se movessem, e a velocidade de rotação do aparato permitiu obter o valor da interação gravitacional entre quaisquer corpos massivos.

Embora a força gravitacional seja a mais fraca, se comparada às outras forças fundamentais (forte, fraca e eletromagnética), para objetos astronômicos, como planetas, luas e estrelas, a magnitude das massas envolvidas torna a interação gravitacional intensa o suficiente para orientar o movimento dos astros celestes.
Compartilhe ideias
A gravidade funciona em todas as escalas!
a ) Junte-se a um colega e pesquisem alguns efeitos da gravidade na Terra, no Sistema Solar, na Via Láctea e além dela.
Resposta: Os estudantes podem responder que na Terra a gravidade nos mantém em sua superfície; no Sistema Solar, ela mantém a Terra e outros planetas e satélites em órbita em torno do Sol; na Via Láctea, ela impede que bilhões de estrelas se dispersem; e, no espaço intergaláctico, ela permite que existam aglomerados de galáxias.
Em 1915, o físico alemão Albert Einstein (1879-1955) publicou a Teoria da Relatividade Geral, revolucionando com isso a maneira de entender a gravidade. Ajustando as ideias de Newton, de que a força da gravidade se dava por meio da ação a distância entre corpos que tinham massa, Einstein descreveu a gravidade como uma deformação (curvatura) no espaço-tempo causada pela presença de massa e energia. Entende-se espaço-tempo como uma estrutura contínua e maleável, na qual todos os eventos do universo ocorrem.

A fim de verificar a previsão da teoria de Einstein de que a deformação do espaço-tempo desviaria a trajetória da luz, equipes de cientistas lideradas pelo astrofísico britânico Arthur Stanley Eddington (1882-1944) viajaram para Sobral, no Ceará, e Porto Príncipe, na África, para acompanhar o eclipse solar de 29 de maio de 1919. Nessa ocasião, em que as estrelas ao lado do Sol ficaram visíveis, observaram que as posições aparentes das estrelas estavam deslocadas em relação às suas posições reais. Com isso, ficou evidenciado que a luz das estrelas estava sendo curvada pela gravidade do Sol, como mostra a figura.
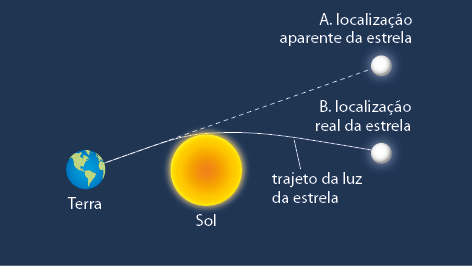
Página 64
Campo gravitacional
Imagens desta página sem proporção e em cores fantasia.
14. O que acontece quando aproximamos um ímã de pregos?
Resposta: Os pregos são atraídos pelo ímã. O objetivo desta questão é levar os estudantes a perceber que existe um campo magnético ao redor de um ímã, que atrai os pregos.
15. Como é chamada a região ao redor de um ímã que é influenciada por ele?
Resposta: Campo magnético.
As interações a distância, como a elétrica, a magnética e a gravitacional, ocorrem em certa região do espaço ao redor de um corpo, denominada campo. A região ao redor de um corpo que tem massa é denominada campo gravitacional. Nessa região, qualquer outro corpo que tem massa é influenciado pela ação da força da gravidade.
O planeta Terra, por exemplo, gera um campo gravitacional. Como a Lua está localizada nesse campo, ela sente a ação da força de atração da Terra. Da mesma forma, a Lua gera um campo gravitacional onde está localizado o planeta, que sente a ação de uma força gravitacional de mesma intensidade, mesma direção e sentido oposto, de acordo com a terceira lei de Newton, da ação e reação.
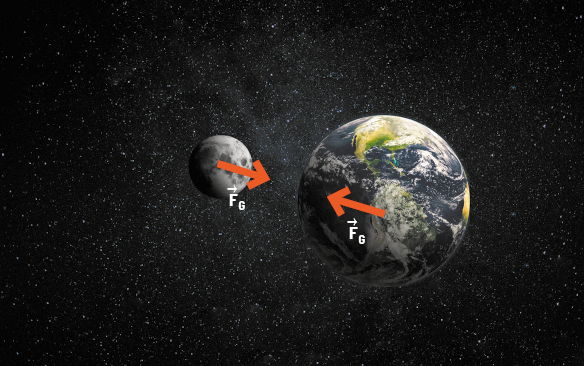
O campo gravitacional gerado por um corpo corresponde a uma grandeza vetorial, com direção que passa pelo seu centro de massa e tem sentido para o corpo, pois a força é sempre de atração. Seu padrão de representação são linhas de campo. Na região onde as linhas são mais próximas umas das outras (mais perto do centro), o campo é mais intenso, e na região onde as linhas estão mais espaçadas entre si (mais afastadas do centro), o campo é menos intenso.
Para determinar a intensidade do campo gravitacional, considere a Terra um referencial inercial e com formato esférico homogêneo, com massa M e raio constante R subscrito T. Considere também que um corpo de prova de massa 'm' é colocado a uma distância 'h' da superfície da Terra, de modo que a distância entre os centros de massa seja R subscrito T mais 'h', conforme representado a seguir.
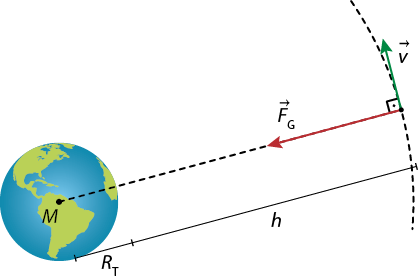
Página 65
Imagens desta página sem proporção e em cores fantasia.
Pela lei da gravitação universal de Newton, tem-se que:
'F' subscrito G é igual a início de fração, numerador: G vezes M vezes 'm', denominador: d elevado ao quadrado, fim de fração implica em 'F' subscrito G é igual a início de fração, numerador: G vezes M vezes 'm', denominador: abre parênteses R subscrito T mais 'h' fecha parênteses elevado ao quadrado, fim de fração implica em início de fração, numerador: 'F' subscrito G, denominador: 'm', fim de fração é igual a início de fração, numerador: G vezes M, denominador: abre parênteses R subscrito T mais 'h' fecha parênteses elevado ao quadrado, fim de fração
Quanto maior a massa 'm', maior a intensidade da força gravitacional 'F' subscrito G, de forma que a razão entre essas duas grandezas, como representado anteriormente, é sempre constante. Porém, pela segunda lei de Newton, da razão entre força e massa temos a aceleração abre parênteses a é igual a 'F' sobre 'm' fecha parênteses, ou seja, a medida da intensidade do campo gravitacional corresponde à medida da intensidade da aceleração da gravidade abre parênteses 'g' fecha parênteses à distância R subscrito T mais 'h' do centro de massa da Terra.
'g' é igual a início de fração, numerador: 'F' subscrito G, denominador: m, fim de fração é igual a início de fração, numerador: G vezes M, denominador: abre parênteses R subscrito T mais 'h' fecha parênteses elevado ao quadrado, fim de fração portanto 'g' é igual a início de fração, numerador: G vezes M, denominador: abre parênteses R subscrito T mais 'h' fecha parênteses elevado ao quadrado, fim de fração
Assim, quando falamos em aceleração da gravidade de um planeta a certa distância, nos referimos à medida do campo gravitacional naquele local. Dessa forma, as unidades de medida metro por segundo quadrado e N barra quilograma são equivalentes.
Para a superfície da Terra, temos:
'g' é igual a início de fração, numerador: G vezes M, denominador: abre parênteses R subscrito T mais 'h' fecha parênteses elevado ao quadrado, fim de fração é igual a início de fração, numerador: abre parênteses 6 vírgula 67 vezes 10 elevado a menos 11 fecha parênteses vezes abre parênteses 5 vírgula 97 vezes 10 elevado a 24 fecha parênteses, denominador: abre parênteses 6 vírgula 37 vezes 10 elevado a 6 mais 0 fecha parênteses elevado ao quadrado, fim de fração é aproximadamente igual a 9 vírgula 8 portanto 'g' é igual a 9 vírgula 8 metros por segundo elevado ao quadrado
Como a Terra não é uma esfera homogênea, com massa distribuída de maneira uniforme, esse valor sofre variações em sua superfície. Mesmo assim, podemos considerá-lo constante em suas proximidades quando calculamos a intensidade da força peso de um corpo de massa 'm'.
Movimento de satélites
Em nosso cotidiano, utilizamos diversos dispositivos eletrônicos que funcionam com o auxílio de satélites artificiais que orbitam a Terra. Entre eles, podemos citar smartphones, televisores e GPS.
Embora sejam aplicações altamente tecnológicas e recentes, todo o fundamento teórico para colocar e manter os satélites artificiais em órbita da Terra baseia-se nos estudos de Kepler e Newton, realizados ainda no século XVII.
A seguir, vamos descrever o movimento de dois corpos que interagem gravitacionalmente, como um satélite artificial que orbita a Terra.
Todo corpo em queda livre, desprezadas as forças de resistência, percorre 5 metros para baixo ao completar 1 segundo de movimento. Quando um corpo é lançado horizontalmente, desprezando-se a resistência do ar, seu movimento vertical será o mesmo, enquanto se moverá horizontalmente para a frente.
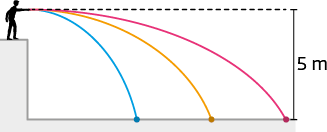
Uma característica geométrica relacionada à curvatura da Terra é que, considerando-se um ponto na superfície da Terra e projetando-se um segmento de reta de 8.000 metros de comprimento, tangente a esse ponto, a superfície se curva aproximadamente 5 metros em relação à extremidade desse segmento de reta.

Dessa forma, se um corpo for lançado na horizontal com velocidade de 8.000 metros por segundo, o que é aproximadamente 29.000 quilômetros por hora, no primeiro segundo de movimento seu deslocamento vertical de 5 metros acompanharia a curvatura do planeta, descrevendo assim uma órbita circular, ou seja, "caindo" ao redor da Terra, e não em direção ao seu centro, como costumamos observar.
Página 66
Imagens desta página sem proporção e em cores fantasia.
A força gravitacional entre a Terra e o corpo lançado será perpendicular ao vetor velocidade, que é tangente a um ponto da superfície da Terra, agindo como uma força centrípeta com variação apenas na orientação da velocidade, e não em seu módulo.
Órbitas de satélites também são descritas pelas leis de Kepler, porém a trajetória elíptica tem excentricidade muito próximo de zero, sendo semelhante a uma circunferência.
O movimento dos satélites já havia sido compreendido por Newton. Na obra O sistema do mundo (1687), ele comparou o movimento da Lua ao de um projétil lançado horizontalmente do topo de uma montanha localizado acima da atmosfera, desprezando assim a resistência do ar. Quanto maior for a intensidade da velocidade horizontal de lançamento, mais distante do topo da montanha o projétil vai tocar o solo da Terra. Assim, com certa velocidade, o corpo "cairia" ao redor da Terra, ou seja, entraria em órbita.
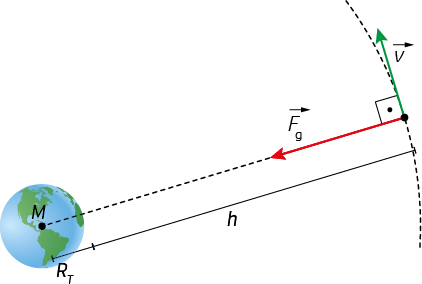

A intensidade da velocidade de órbita de um corpo de massa 'm' lançado em órbita a uma altura 'h' da superfície da Terra, de massa M e raio R subscrito T, é dada por:
'F' subscrito c p é igual a 'F' subscrito G implica em início de fração, numerador: 'm' vezes v elevado ao quadrado, denominador: R subscrito T mais 'h', fim de fração é igual a início de fração, numerador: G vezes M vezes 'm', denominador: abre parênteses R subscrito T mais 'h' fecha parênteses elevado ao quadrado, fim de fração implica em v é igual a início de raiz quadrada; início de fração, numerador: G vezes M, denominador: R subscrito T mais 'h', fim de fração fim de raiz quadrada
Essa velocidade representa a velocidade média orbital, já que a velocidade instantânea pode sofrer variações durante o movimento em razão de alguns fatores, como o formato irregular da Terra e seu movimento de rotação. A velocidade orbital de um corpo não depende de sua massa, apenas da massa do planeta que ele orbita abre parênteses M fecha parênteses e da distância da órbita em relação ao centro de massa do planeta abre parênteses R subscrito T mais 'h' fecha parênteses.
A velocidade média orbital da Estação Espacial Internacional, por exemplo, que orbita a Terra a 400 quilômetros de sua superfície, é cerca de 7.669 vírgula 3 metros por segundo ou 27.609 vírgula 5 quilômetros por hora. É possível verificar esses valores aplicando a equação de velocidade média orbital definida anteriormente. Confira a seguir.
v é igual a início de raiz quadrada; início de fração, numerador: G vezes M, denominador: R subscrito T mais 'h', fim de fração fim de raiz quadrada é igual a início de raiz quadrada; início de fração, numerador: abre parênteses 6 vírgula 67 vezes 10 elevado a menos 11 fecha parênteses vezes abre parênteses 5 vírgula 97 vezes 10 elevado a 24 fecha parênteses, denominador: abre parênteses 6 vírgula 37 vezes 10 elevado a 6 mais 400.000 fecha parênteses, fim de fração fim de raiz quadrada é aproximadamente igual a 7669 vírgula 3 portanto v é aproximadamente igual a 7.669 vírgula 3 metros por segundo
Professor, professora: Diga aos estudantes que os valores mostrados foram obtidos com base na geometria da Terra. Em um caso real, no qual tentássemos colocar um corpo em órbita tendo como base o solo, lançando-o horizontalmente com velocidade de 8.000 metros por segundo, não poderíamos desprezar a resistência do ar, que apresentaria um valor altíssimo. Ainda assim despreza-se a resistência do ar, não só por se tratar de um caso teórico, mas principalmente porque a lógica permanece inalterada para colocarmos um objeto em órbita quando ele estiver fora da atmosfera terrestre, onde não haveria resistência alguma.
16. A velocidade de órbita de um corpo a 1 metro da superfície da Terra é maior ou menor do que a de um corpo a 1 quilômetro de altura em relação à superfície da Terra? Explique.
Resposta: Maior. Quanto mais distante da superfície da Terra estiver um satélite, menor sua velocidade orbital e, consequentemente, maior seu período.
Página 67
Um satélite que orbita a Terra a cerca de 280 quilômetros de altitude tem um período de aproximadamente 90 minutos. Já um satélite a uma altitude equivalente a 5,5 vezes o raio da Terra, cerca de 35.000 quilômetros, tem um período próximo de 24 horas, que é o mesmo período de rotação da Terra. Para uma órbita sobre a linha do equador, esse satélite estará sempre acima de um mesmo ponto do planeta, sendo denominado satélite geoestacionário.
Um satélite geoestacionário também tem a mesma velocidade angular abre parênteses ômega fecha parênteses da Terra, pois ambos percorrem 360 graus ou 2 vezes pi rad no mesmo intervalo de tempo (24 horas).
O Satélite de Coleta de Dados 1 (SCD-1) foi o primeiro a ser projetado, construído, testado e operado no Brasil, pelo Instituto Nacional de Pesquisas Espaciais (INPE), tendo sido lançado em 1993 com o auxílio da Agência Espacial Norte-Americana (Nasa, da sigla em inglês). Ele tem o formato de um prisma octogonal, com 1 metro de largura máxima, 1 vírgula 45 metro de altura, e massa de 115 quilogramas.

A órbita do satélite SCD-1 está localizada a 750 quilômetros acima da superfície da Terra, completando uma volta em aproximadamente 1 hora 40 minutos.
17. Determine o número de voltas completas abre parênteses n fecha parênteses que o SCD-1 executa ao redor da Terra no período de um dia.
Resposta: 14 voltas, aproximadamente.

O conhecimento sobre o movimento de satélites em torno da Terra permitiu o envio de satélites artificiais e sondas espaciais para orbitar outros corpos do Sistema Solar, como Júpiter, Saturno, Marte e a Lua. Isso nos possibilitou obter dados e informações sobre a composição e estrutura desses astros.
Para sistemas de dois corpos sujeitos à ação de única e exclusivamente suas forças gravitacionais, como uma estrela e um planeta ou um planeta e um satélite artificial, os movimentos descrevem trajetórias previsíveis com o uso da Matemática. No entanto, adicionar um terceiro corpo ao sistema significa elevar a complexidade da compreensão e previsão dos movimentos, em razão de interações gravitacionais mútuas. Esse desafio é denominado Problema dos Três Corpos.
Imagem sem proporção e em cores fantasia.

O matemático e físico francês Jules Henri Poincaré (1854-1912), ao investigar esse problema, descobriu que uma pequena alteração nas condições desse sistema de três corpos pode levar a resultados drasticamente diferentes. Essa imprevisibilidade e complexidade é a ideia central da Teoria do Caos, definida mais tarde por ele.
Isso nos leva a concluir que o comportamento do Cosmos é complexo, e sua imprevisibilidade desafia toda a comunidade científica.
Nosso Sistema Solar também pode se enquadrar nessa situação. O Sol, a Terra e a Lua podem ser considerados um sistema de três corpos, ou até mesmo sistemas com mais corpos, se considerarmos os demais planetas. No entanto, como o Sol tem massa muito superior à de qualquer astro do Sistema Solar, a influência dos planetas e dos outros astros sobre ele é insuficiente para qualquer consideração de alteração.
Página 68
ATIVIDADES
Imagens desta página sem proporção e em cores fantasia.
1. A intensidade da força gravitacional com que um corpo de massa M atrai outro corpo de massa 'm' é 'F' quando separados por uma distância d. Caso a distância entre eles fosse dobrada e a massa dos corpos fosse diminuída, cada uma, para metade, a intensidade da força gravitacional seria de:
a ) 16 'F'
b ) 2 'F'
c ) 'F'
d ) 'F' sobre 2
e ) 'F' sobre 16
Resposta: Alternativa e. Resolução nas Orientações para o professor.
2. Os esquemas a seguir representam a atração gravitacional entre um planeta e sua lua. Ordene, em sequência crescente, as forças atrativas entre cada par mostrado.
A.
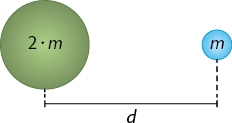
B.
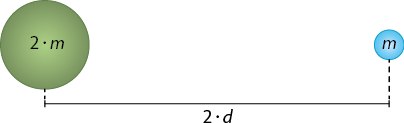
C.
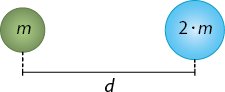
D.
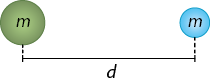
Resposta: B é menor do que D é menor do que A é igual a C.
3. Sabe-se que as marés são causadas principalmente pela influência gravitacional da Lua. Isso quer dizer que a atração da Lua sobre a Terra é maior do que a do Sol sobre o planeta? Justifique sua resposta.
Resposta: Não, a força de atração do Sol sobre a Terra é maior que a da Lua sobre nosso planeta. As marés causadas pela Lua são mais intensas porque a diferença de atração, comparando o lado mais próximo da Terra com o mais distante, tem maior variação para a Lua do que para o Sol.
4. O planeta Júpiter tem massa 300 vezes maior que a da Terra. Isso pode dar a ideia de que sua aceleração da gravidade é muitas vezes maior que a de nosso planeta. No entanto, o que se verifica é que a aceleração da gravidade de Júpiter é menos de 3 vezes maior que a da Terra. Explique por que isso ocorre.
Resposta: Isso ocorre porque o raio de Júpiter é cerca de 10 vezes maior que o raio da Terra.
5. De acordo com a Nasa, mais de 500.000 objetos que fazem parte do lixo espacial estão orbitando a Terra. Considere uma peça esférica de massa 25 quilogramas que orbita a Terra a uma altura da superfície de quatro raios terrestres. Determine a intensidade do campo gravitacional na peça em órbita e a força peso sobre ela. Use 'g' é igual a 9 vírgula 8 metros por segundo elevado ao quadrado.
Resposta: 'g' subscrito P é igual a 0 vírgula 4 metro por segundo elevado ao quadrado e 'F' subscrito P é igual a 10 newtons. Resolução nas Orientações para o professor.
6. O gráfico que melhor representa como a intensidade da força gravitacional entre dois corpos varia com a distância é:
A.
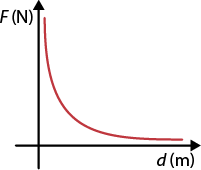
B.
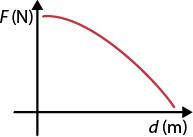
C.

D.

E.

Resposta: Alternativa a.
7. Um satélite artificial está em órbita ao redor da Terra. Faça um esboço dessa configuração, representando, com um vetor, a resultante das forças que agem sobre o satélite.
Resposta: A resultante das forças é radial com sentido para o centro do planeta Terra. Comentários nas Orientações para o professor.
Atividade(s) adaptada(s) acessível(is)
7. Um satélite artificial está em órbita ao redor da Terra. Descreva essa configuração identificando as características da resultante das forças que agem sobre o satélite.
Resposta: Espera-se que os estudantes comentem que a órbita do satélite em torno da Terra pode ter formato de circunferência e que a resultante das forças que agem sobre o satélite é centrípeta, ou seja, é perpendicular à velocidade do satélite e aponta para o centro da órbita (centro da Terra).
Página 69
8. O satélite brasileiro Amazônia-1 foi lançado em 2021. Seu principal objetivo é fornecer imagens de sensoriamento remoto para monitorar a região amazônica, em especial as zonas de desmatamento.
O satélite está orbitando a Terra a cerca de 750 quilômetros de altitude. Qual é a intensidade da aceleração gravitacional em razão do campo gravitacional terrestre a essa altitude? Considere o raio da Terra de aproximadamente 6 vírgula 4 vezes 10 elevado a 6 m.

Resposta: 'g' é igual a 7 vírgula 8 metros por segundo elevado ao quadrado, aproximadamente. Resolução nas Orientações para o professor.
9. Sobre o movimento de satélites artificiais em torno da Terra, avalie as afirmativas a seguir.
01 ) Para órbitas de raios menores, a velocidade orbital do satélite deve ser maior.
02 ) Os satélites artificiais se mantêm em órbita porque a força gravitacional sobre eles é nula.
04 ) Ocupando órbitas de mesmo raio, dois satélites de massas diferentes terão velocidades orbitais iguais.
08 ) Os satélites artificiais geoestacionários completam uma volta em torno da Terra em um intervalo de 24 horas.
16 ) Os satélites artificiais não obedecem às leis de Kepler porque têm órbitas com formato praticamente circular.
Resposta: Soma: 01 mais 0 4 mais 0 8 é igual a 13. Comentários nas Orientações para o professor.
10. O telescópio espacial Hubble comemorou aniversário de 35 anos de funcionamento em 2025. No lançamento, o Hubble tinha massa de aproximadamente 11.100 quilogramas e a partir de 2009 ficou com 12.250 quilogramas, após missão de manutenção e instalação de novos equipamentos. Com a adição de massa, o que aconteceu com a velocidade orbital do telescópio?
Resposta: A velocidade orbital do telescópio Hubble não se alterou, pois ela não depende da massa do corpo em órbita.
11. Um dos objetivos da Astronomia moderna é a descoberta e análise de planetas fora do Sistema Solar. Suponha que tenha sido encontrado um planeta que possui 5 vezes a massa da Terra e raio equivalente ao dobro do raio terrestre. Qual seria a aceleração da gravidade na superfície desse planeta? (Use 'g' é igual a 9 vírgula 8 metros por segundo elevado ao quadrado).
Resposta: 'g' subscrito p é igual a 12 vírgula 25 metros por segundo elevado quadrado. Resolução nas Orientações para o professor.
12. O gráfico a seguir mostra a variação da força gravitacional em função da distância de uma estrela que é orbitada por um corpo celeste de massa 5 vezes 10 elevado a 30 quilograma. Qual é a velocidade média orbital desse corpo que está a uma distância de 1 vírgula 57 vezes 10 elevado a 20 m do centro de massa da estrela?
Gráfico da força gravitacional em função da distância em relação a uma estrela
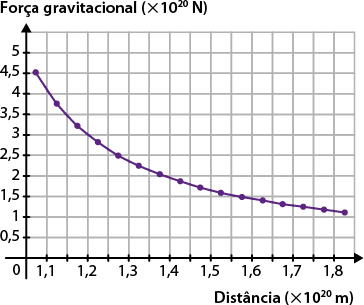
Fonte de pesquisa: HEWITT, Paul G. Física conceitual. Tradução: Trieste Freire Ricci. 12. ed. Porto Alegre: Bookman, 2015. p. 165.
Resposta: v é igual a 6 vírgula 86 vezes 10 elevado a 4 metro por segundo. Resolução nas Orientações para o professor.
Página 70
CAPÍTULO5
Movimentos na Terra
A ação da gravidade
Muitas pessoas já passaram pela mesma situação retratada na fotografia. Em apenas alguns segundos, um pequeno acidente aconteceu. Mas por que os corpos caem quando são soltos? Você já fez essa pergunta?

Como visto anteriormente, uma das interações fundamentais da natureza é a gravidade. Em razão dessa interação, os corpos se atraem gravitacionalmente. No entanto, se as massas envolvidas forem pequenas, é difícil percebermos os efeitos dessa força de atração. Quando um dos corpos tem massa suficientemente grande, como a Terra, conseguimos notar a atuação da gravidade por meio de alguns movimentos, por exemplo, queda livre e lançamentos vertical, horizontal e oblíquo.
Queda livre
O movimento de queda em decorrência do campo gravitacional da Terra pode ser observado quando abandonamos um corpo de certa altura.
1. Por que você acha que todos os corpos próximos à superfície da Terra são atraídos para ela?
Resposta: Porque sofrem a ação de uma força que os atrai em direção à superfície da Terra.
O paraquedista da fotografia, por exemplo, utiliza esse fato em sua prática esportiva. Após saltar pela porta do avião, ele inicia um movimento acelerado na direção do centro da Terra e no sentido do solo, em razão da força gravitacional que atua sobre ele.

Na Antiguidade, o filósofo grego Aristóteles (384 a.C.-322 a.C.), com base em observações da natureza, afirmava que após uma primeira aceleração para sair do repouso, os corpos caíam com uma velocidade constante, que dependia de suas massas.
Professor, professora: Comente com a turma que, em muitos casos, a força de resistência do ar é prejudicial para algumas ações. Cite as pesquisas relacionadas à aerodinâmica, principalmente a automobilística, a fim de melhorar o desempenho dos veículos e reduzir o consumo de combustível.
Na Idade Moderna, o cientista italiano Galileu Galilei (1564-1642), mesmo não sendo o primeiro a apontar problemas nas ideias de Aristóteles, desenvolveu práticas de observação e experimentação que as refutaram definitivamente.
Variando a massa das esferas e o ângulo de inclinação da rampa, Galileu notou que os movimentos não eram uniformes, mas acelerados. Percebeu ainda que a aceleração adquirida dependia apenas da inclinação da rampa, sendo a direção vertical a de maior aceleração.
A imagem a seguir representa os deslocamentos executados por uma esfera em intervalos de tempo iguais.
Imagem sem proporção e em cores fantasia.

Página 71
Em seus experimentos com rampas, ao manter constante o ângulo de inclinação da rampa e o corpo partindo do repouso, Galileu percebeu uma relação entre a distância percorrida e o intervalo de tempo necessário para o corpo percorrer essa distância.
Ele notou que em um intervalo de tempo 't' um corpo percorre uma distância d. Se o intervalo de tempo considerado fosse o dobro do primeiro, a distância a ser percorrida era quadruplicada; ao passo que, se o intervalo de tempo fosse triplicado, a distância aumentaria 9 vezes. Com base nisso, sua conclusão foi: se um móvel, partindo do repouso, cai com um movimento uniformemente acelerado, o espaço percorrido em queda é diretamente proporcional ao quadrado do tempo de queda.
Galileu também fez observações deixando esferas que haviam descido por um plano inclinado subir por outro plano inclinado. Assim, verificou que, quanto menor a inclinação do plano de subida, maior era o intervalo de tempo necessário para a esfera atingir o repouso. Com essas e outras investigações, ele concluiu que, se a esfera que desceu por um plano inclinado atingisse um plano horizontal infinitamente longo, ela deveria se manter em movimento uniforme por tempo indeterminado. Essa conclusão ficou conhecida como princípio da inércia de Galileu.
No entanto, o cientista italiano observou que as esferas atingiam o repouso após percorrer certa distância nos planos horizontais, propondo que isso acontecia por conta da ação das forças de atrito entre a esfera e a superfície do plano e pela ação da resistência do ar.
Dessa forma, podemos concluir que é a resistência do ar que faz corpos de diferentes massas executarem movimentos de queda com velocidades diferentes, e não as massas em si, como acreditava Aristóteles.
A força de resistência do ar (ou força de arrasto) depende da velocidade do corpo e da área de contato com o ar. Quanto mais rápido o corpo se move, maior é a quantidade de partículas de ar que entram em contato com ele. O paraquedista citado anteriormente, mantendo o corpo na horizontal, em determinado momento da queda, passa a desenvolver um movimento com velocidade constante (chamada de velocidade terminal), pois a força de resistência do ar adquire o mesmo valor da força gravitacional.
Mas e se a resistência do ar puder ser desprezada?
Em 1971, o astronauta estadunidense David R. Scott (1932 -) realizou um experimento na superfície da Lua, no qual ele abandonou, da mesma altura, uma pena de falcão e um martelo. Os dois objetos chegaram ao solo lunar ao mesmo tempo, pois não há resistência do ar.

Compartilhe ideias
Os corpos em queda livre podem sofrer a ação da força de resistência do ar, modificando sua velocidade durante a queda.
a ) Junte-se a um colega para observar na prática a resistência oferecida para os movimentos que ocorrem no ar. Para isso, providenciem duas folhas de papel idênticas, uma aberta e outra amassada. Primeiro, soltem simultaneamente da mesma altura a folha aberta (paralelamente ao chão) e a amassada e observem qual delas toca primeiro o chão. Em seguida, coloquem a folha aberta e a amassada sobre um caderno e abandonem o caderno de certa altura, observando ambas. Agora, amassem a folha de papel que estava aberta e soltem-nas novamente da mesma altura, simultaneamente, e percebam o que ocorre nessa situação. Para finalizar, conversem sobre a atividade realizada e anotem suas conclusões no caderno.
Resposta: Na primeira situação, as folhas chegam ao chão em intervalos de tempo diferentes; já na segunda situação, o conjunto chega ao chão ao mesmo tempo. Comentários nas Orientações para o professor.
Página 72
Imagens desta página sem proporção e em cores fantasia.
Quando um corpo cai em razão somente da ação da gravidade, desprezando a resistência do ar, dizemos que ele está em queda livre. Isso ocorre no vácuo ou em um local onde a força de resistência do ar pode ser desprezada, como para pequenos deslocamentos próximos à superfície da Terra.
Na queda livre, a aceleração a que todos os corpos estão sujeitos é a aceleração gravitacional abre parênteses 'g' fecha parênteses. Esta é característica do planeta ou astro celeste que estamos considerando.
Como a aceleração gravitacional sofre pequenas alterações na superfície da Terra, sendo maior nos polos e menor no equador, no estudo da queda livre, vamos considerá-la constante para toda a superfície terrestre com módulo 'g' é igual a 9 vírgula 8 metros por segundo elevado ao quadrado. Muitas vezes, esse valor é arredondado para 10 metros por segundo elevado ao quadrado, para facilitar a análise de algumas situações.
A queda livre é um movimento apenas na direção vertical. Dessa maneira, vamos considerar o seguinte: se o referencial vertical adotado tiver sentido para cima, considera-se a aceleração da gravidade negativa abre parênteses menos 'g' fecha parênteses; se o referencial vertical adotado tiver sentido para baixo, considera-se a aceleração da gravidade positiva abre parênteses mais 'g' fecha parênteses.
Dica
Uma aceleração de módulo 9 vírgula 8 metros por segundo elevado ao quadrado significa que, a cada 1 segundo em queda livre, a velocidade do corpo varia em 9 vírgula 8 metros por segundo.
A.

B.

O movimento de queda livre se enquadra em um tipo de movimento chamado de Movimento Uniformemente Variado (MUV), caracterizado pela variação constante no módulo da velocidade do móvel ao longo da trajetória, ou seja, um movimento com aceleração constante – nesse caso, a aceleração gravitacional 'g'.
A aceleração é uma grandeza vetorial que, dependendo do tipo de trajetória executada pelo corpo em movimento, pode ser dividida em duas componentes:
- aceleração tangencial abre parênteses a subscrito t fecha parênteses: relacionada com variações na intensidade da velocidade, pois atua na mesma direção da velocidade;
- aceleração centrípeta abre parênteses a subscrito c fecha parênteses: relacionada com variações na orientação da velocidade.
Trajetória retilínea

A variação apenas na intensidade da velocidade caracteriza um movimento retilíneo uniformemente variado (MRUV); a aceleração centrípeta é nula, e a aceleração abre parênteses expressão com detalhe acima, início da expressão, a, fim da expressão, início do detalhe acima, seta para a direita, fim do detalhe acima fecha parênteses é dada pela aceleração tangencial.
expressão com detalhe acima, início da expressão, a, fim da expressão, início do detalhe acima, seta para a direita, fim do detalhe acima é igual a expressão com detalhe acima, início da expressão, a, fim da expressão, início do detalhe acima, seta para a direita, fim do detalhe acima subscrito t mais expressão com detalhe acima, início da expressão, a, fim da expressão, início do detalhe acima, seta para a direita, fim do detalhe acima subscrito c portanto expressão com detalhe acima, início da expressão, a, fim da expressão, início do detalhe acima, seta para a direita, fim do detalhe acima é igual a expressão com detalhe acima, início da expressão, a, fim da expressão, início do detalhe acima, seta para a direita, fim do detalhe acima subscrito t
Trajetória curvilínea
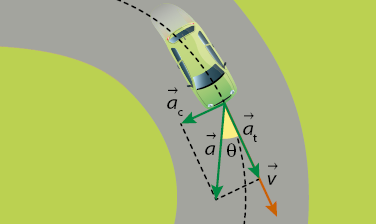
A variação na intensidade e na orientação da velocidade caracteriza um movimento circular uniformemente variado (MCUV); a aceleração abre parênteses expressão com detalhe acima, início da expressão, a, fim da expressão, início do detalhe acima, seta para a direita, fim do detalhe acima fecha parênteses é dada pela soma das acelerações tangencial e centrípeta.
expressão com detalhe acima, início da expressão, a, fim da expressão, início do detalhe acima, seta para a direita, fim do detalhe acima é igual a expressão com detalhe acima, início da expressão, a, fim da expressão, início do detalhe acima, seta para a direita, fim do detalhe acima subscrito t mais expressão com detalhe acima, início da expressão, a, fim da expressão, início do detalhe acima, seta para a direita, fim do detalhe acima subscrito c
Professor, professora: Explique que a única diferença entre os movimentos circulares e os retilíneos consiste na direção dessa grandeza. A componente da aceleração com a mesma direção da velocidade do móvel é chamada aceleração tangencial. Nos casos em que o corpo tem apenas aceleração tangencial, ele vai descrever movimentos retilíneos. Já a componente da aceleração orientada perpendicularmente à velocidade do corpo é definida como aceleração centrípeta.
Página 73
Na queda livre, a aceleração é constante e tangencial à trajetória. Portanto, podemos analisar esse movimento com base na equação da aceleração média, dada por:
a é igual a início de fração, numerador: delta v, denominador: delta 't', fim de fração implica em a é igual a início de fração, numerador: v menos v subscrito 0, denominador: 't' menos 't' subscrito 0, fim de fração
em que a é a aceleração em metro por segundo quadrado; delta v é a variação de velocidade em metro por segundo; delta 't' é o intervalo de tempo em s; v e v subscrito 0 são as velocidades final e inicial em metro por segundo; 't' e 't' subscrito 0 são os tempos final e inicial em segundo.
Dessa equação, obtemos uma relação entre as velocidades abre parênteses v fecha parênteses e os instantes de tempo abre parênteses 't' fecha parênteses denominada função horária das velocidades do MRUV.
a é igual a início de fração, numerador: delta v, denominador: delta 't', fim de fração implica em delta v é igual a a vezes delta 't' implica em v menos v subscrito 0 é igual a a vezes abre parênteses 't' menos 't' subscrito 0 fecha parênteses implica em v é igual a v subscrito 0 mais a vezes abre parênteses 't' menos 't' subscrito 0 fecha parênteses
Considerando 't' subscrito 0 é igual a 0 e a é igual a 'g', tem-se:
v é igual a v subscrito 0 mais 'g' vezes 't'
Com essa função, é possível obter os valores de velocidade para qualquer instante de tempo. Já a função horária das posições para o MRUV é dada por:
's' é igual a 's' subscrito 0 mais v subscrito 0 vezes 't' mais início de fração, numerador: a vezes 't' elevado ao quadrado, denominador: 2, fim de fração
em que 's' é a posição final; 's' subscrito 0, a posição inicial; v subscrito 0, a velocidade inicial; a, a aceleração do móvel; e 't', o instante de tempo. Tal função de 2º grau expressa a dependência da posição 's' do corpo em MRUV em relação aos instantes de tempo 't'. Para um corpo em queda livre, geralmente substituímos 's' por y para representar as posições do corpo na vertical e a aceleração a pela aceleração da gravidade 'g', que nos dá:
y é igual a y subscrito 0 mais v subscrito 0 vezes 't' mais início de fração, numerador: 'g' vezes 't' elevado ao quadrado, denominador: 2, fim de fração

A equação anterior representa matematicamente a conclusão obtida por Galileu em seus experimentos com a queda de corpos: a distância percorrida é proporcional ao quadrado do tempo de queda. Entretanto, o cientista italiano utilizou uma abordagem diferente para descrever o movimento uniformemente acelerado: Galileu aplicou conceitos de proporção e progressão geométrica para mostrar que a distância percorrida por um corpo em queda é proporcional ao quadrado do tempo de queda. Tais abordagens permitiram estabelecer uma base sólida para a mecânica clássica.
Há outra equação importante no estudo dos corpos em queda livre, que relaciona a posição, a velocidade e a aceleração dos corpos, sem a necessidade de considerar um intervalo de tempo. Tal relação matemática é chamada de equação de Torricelli.
O físico e matemático italiano Evangelista Torricelli (1608-1647) desenvolveu estudos sobre fluidos em repouso e em movimento e verificou que a velocidade horizontal de um jato de água jorrando por um pequeno orifício é dada por:
v é igual a início de raiz quadrada; 2 vezes 'g' vezes H fim de raiz quadrada
Dica
Não se esqueça de atentar ao sentido do referencial vertical: se orientado para cima, utilizar menos 'g'; se orientado para baixo, utilizar mais 'g'.
Imagem sem proporção e em cores fantasia.
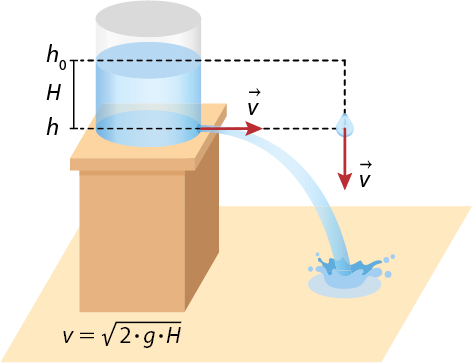
Esse valor é igual ao da velocidade de uma única gota de água, que, partindo do repouso, percorre a mesma distância H em queda livre.
Página 74
Dessa forma, a semelhança entre a velocidade de lançamento de um jato de água e a velocidade de queda livre de uma gota em MRUV possibilitou o estudo desse movimento pela relação entre velocidade abre parênteses v fecha parênteses e posição abre parênteses y fecha parênteses, ou seja, uma relação que não depende do tempo.
Aplicando os estudos de Torricelli na análise do movimento dos corpos em queda livre, obtemos a seguinte relação:
v elevado ao quadrado é igual a v subscrito 0 início sobrescrito, 2, fim sobrescrito mais 2 vezes 'g' vezes delta y ou v elevado ao quadrado é igual a v subscrito 0 início sobrescrito, 2, fim sobrescrito mais 2 vezes 'g' vezes abre parênteses y menos y subscrito 0 fecha parênteses
Dica
Note que a equação de Torricelli não envolve o tempo, ou seja, não corresponde a uma equação horária.
ATIVIDADES RESOLVIDAS
R1. A Big Tower é uma das muitas atrações de um parque de diversões brasileiro e tem nada menos que 100 metros de altura, equivalente a um prédio de mais de 30 andares. Durante a queda, o elevador chega a uma velocidade de aproximadamente 120 quilômetros por hora. Então, quem disse que a Física não está presente nos parques de diversão?

De acordo com os dados apresentados e desconsiderando a força de resistência do ar e outras forças dissipativas, supondo que ele se move em queda livre por cerca de 85 metros até os freios serem acionados, qual é a velocidade atingida pelo elevador no intervalo de queda livre? Compare seu resultado com o valor real apresentado no enunciado, discutindo o motivo dessa diferença. Adote o valor da aceleração da gravidade local de 10 metros por segundo quadrado.
Resolução
Consideram-se o referencial na vertical com sentido para baixo, a posição inicial em que o elevador é abandonado y subscrito 0 é igual a 0, a velocidade inicial v subscrito 0 é igual a 0 (repouso) e a posição final de queda livre y é igual a 85 metros.
Como não temos o intervalo de tempo, podemos utilizar a equação de Torricelli para calcular o valor da velocidade de queda:
v elevado ao quadrado é igual a v subscrito 0 início sobrescrito, 2, fim sobrescrito mais 2 vezes 'g' vezes delta y implica em v elevado ao quadrado é igual a 0 elevado ao quadrado mais 2 vezes 10 vezes 85 implica em v elevado ao quadrado é igual a 1.700 implica em
implica em v é igual a raiz quadrada de 1.700 portanto v é aproximadamente igual a 41 vírgula 2 metros por segundo ou v é aproximadamente igual a 148 quilômetros por hora
Dica
Essa diferença entre o valor encontrado e o valor real fornecido pelo site oficial se dá pelo fato de que, ao tratar esse movimento como uma queda livre, são desprezadas todas as forças dissipativas que atuam diminuindo a velocidade de queda do brinquedo. Além disso, usamos uma distância aproximada de queda livre.
Lançamento vertical
É tradição em formaturas que, ao final da cerimônia, os formandos lancem seus chapéus verticalmente para cima, comemorando sua conquista.

Essa situação exemplifica um lançamento vertical, no qual corpos são arremessados na direção vertical, com velocidade inicial diferente de zero. Nesse tipo de lançamento, o corpo pode ser lançado tanto para cima quanto para baixo. Em ambos os casos, desprezando a resistência do ar, o movimento ocorre com aceleração constante e igual à aceleração da gravidade.
No lançamento vertical para baixo, o corpo inicia o movimento de queda livre com determinada velocidade vertical, que aumenta de valor em razão da aceleração da gravidade, como o movimento de algumas aves marinhas, que mergulham para buscar alimentos na água.
Página 75
2. O que acontece quando um objeto é arremessado para cima?
Resposta: O objeto continua a se mover para cima por algum tempo e depois retorna.
No lançamento vertical para cima, o corpo inicia um movimento contrário à ação da gravidade, por isso sua velocidade diminui durante a subida até parar, inverter seu movimento e começar a descer.
Considere uma peteca lançada verticalmente para cima com uma velocidade inicial de 15 metros por segundo. Desprezando a resistência do ar e adotando um referencial vertical com sentido para cima abre parênteses 'g' é igual a menos 10 metros por segundo elevado ao quadrado fecha parênteses, com origem na posição do lançamento abre parênteses y subscrito 0 é igual a 0 fecha parênteses, as funções horárias da velocidade e da posição são:
v é igual a v subscrito 0 mais 'g' vezes 't' portanto v é igual a 15 menos 10 vezes 't'
y é igual a y subscrito 0 mais v subscrito 0 vezes 't' mais início de fração, numerador: 'g' vezes 't' elevado ao quadrado, denominador: 2, fim de fração implica em y é igual a 0 mais 15 vezes 't' menos início de fração, numerador: 10 vezes 't' elevado ao quadrado, denominador: 2, fim de fração portanto y é igual a 15 vezes 't' menos 5 vezes 't' elevado ao quadrado
O movimento da peteca é representado a seguir. Note que durante o movimento de subida sua velocidade diminui gradualmente, descrevendo um MRUV retardado, pois o movimento está contra a aceleração da gravidade. Portanto, a peteca sobe até atingir velocidade nula, com tempo de subida igual a:
v é igual a 15 menos 10 vezes 't' implica em 0 é igual a 15 menos 10 vezes 't' portanto 't' é igual a 1 vírgula 5 segundo
Como a desaceleração na subida é a mesma aceleração na descida, o intervalo de tempo de descida é igual ao de subida. Assim, o tempo total para que a peteca volte à posição inicial é de 3 segundos.
Já o movimento de descida corresponde a um MRUV acelerado, pois é a favor da aceleração da gravidade, e a velocidade da peteca aumenta de forma gradual. Contudo, a descida é contrária ao referencial adotado – isso é indicado pelo sentido dos vetores e pelo sinal negativo da velocidade.
Como a resistência do ar foi desprezada, ao retornar para a mão da pessoa, no instante 3 segundos, a peteca tem velocidade de mesmo valor da velocidade inicial, mas com sentido contrário. Logo:
v é igual a 15 menos 10 vezes 3 implica em v é igual a 15 menos 30 portanto v é igual a menos 15 metros por segundo
As posições da peteca durante o movimento também estão indicadas na imagem. Podemos perceber que a altura máxima atingida corresponde à posição no instante 1 vírgula 5 segundo, quando o objeto atinge o repouso e ocorre a inversão no sentido do movimento. O valor da altura máxima pode ser obtido usando a função horária das posições, portanto:
y é igual a 15 vezes 't' menos 5 vezes 't' elevado ao quadrado implica em y é igual a 15 vezes 1 vírgula 5 menos 5 vezes 1 vírgula 5 elevado ao quadrado portanto y é igual a 11 vírgula 25 metros
Imagem sem proporção e em cores fantasia.
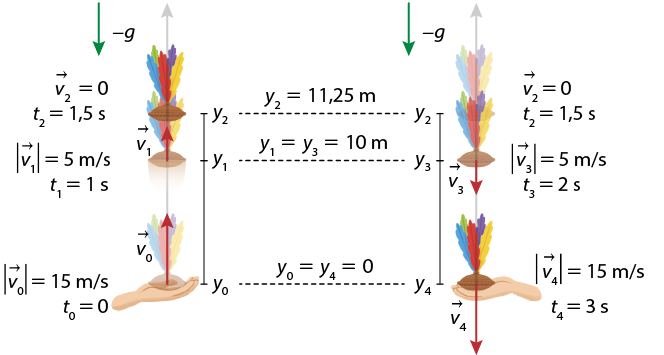
Perceba que no lançamento vertical a peteca passou duas vezes em cada posição (com exceção da posição de altura máxima), em instantes diferentes e com velocidades de mesmo valor, mas com sentidos contrários.
Página 76
De maneira geral, vemos que objetos lançados verticalmente para cima têm sua velocidade diminuída até atingir o repouso no ponto mais alto da trajetória. No entanto, como a força gravitacional continua atuando sobre ele, o corpo cai em queda livre, com aceleração constante, de modo que a velocidade final tem módulo igual ao da velocidade inicial de lançamento, quando o corpo retorna à mesma altura de lançamento.
3. No ponto mais alto da trajetória de um corpo que foi lançado verticalmente para cima, qual é o valor da aceleração do corpo?
Resposta: A aceleração do corpo equivale à aceleração da gravidade a é igual a 'g' é igual a 9 vírgula 8 metros por segundo elevado ao quadrado, ou aproximadamente 'g' é igual a 10 metros por segundo quadrado.
É possível identificar lançamentos verticais em algumas modalidades esportivas, em várias tarefas do dia a dia e também em apresentações artísticas, como exemplificado a seguir.



ATIVIDADES RESOLVIDAS
R2. A ginástica de trampolim, popular no universo circense, surgiu na década de 1930 e se tornou um esporte olímpico em 2000, nos jogos de Sydney, na Austrália. Um atleta, ao realizar um salto, alcançou a altura de 7,2 metros. Considere 'g' é igual a 10 metros por segundo quadrado.
a ) Qual é a velocidade inicial do atleta em seu salto?
Resolução
Considerando o sentido do referencial adotado crescente para cima, a aceleração da gravidade 'g' deve ser negativa.
Como não temos o valor do intervalo de tempo do movimento, vamos utilizar a equação de Torricelli. Sabendo que a altura máxima atingida foi de 7 vírgula 2 metros e que a velocidade é nula no ponto mais alto da trajetória, tem-se:
v elevado ao quadrado é igual a v subscrito 0 início sobrescrito, 2, fim sobrescrito menos 2 vezes 'g' vezes delta y implica em 0 elevado ao quadrado é igual a v subscrito 0 início sobrescrito, 2, fim sobrescrito menos 2 vezes 10 vezes 7 vírgula 2 implica em v subscrito 0 início sobrescrito, 2, fim sobrescrito é igual a 144 implica em v subscrito 0 é igual a raiz quadrada de 144 portanto v subscrito 0 é igual a 12 metros por segundo
b ) Quanto tempo durou o movimento de subida do atleta?
Resolução
Usando a equação horária da velocidade e o valor encontrado para a velocidade inicial do atleta e lembrando que a velocidade na altura máxima é nula, tem-se:
v é igual a v subscrito 0 menos 'g' vezes 't' implica em 0 é igual a 12 menos 10 vezes 't' implica em 't' é igual a 12 sobre 10 portanto 't' é igual a 1 vírgula 2 segundo
c ) Em qual instante de tempo e com qual valor de velocidade o atleta retornou ao solo?
Resolução
Desprezando-se a resistência do ar, o tempo de subida é igual ao tempo de descida, então o tempo total do salto é de:
't' subscrito total é igual a 't' subscrito subida mais 't' subscrito descida implica em 't' subscrito total é igual a 1 vírgula 2 mais 1 vírgula 2 portanto 't' subscrito total é igual a 2 vírgula 4 segundos
que corresponde ao instante em que o atleta volta para o solo.
Já a velocidade tem o mesmo módulo da velocidade inicial, porém com sentido contrário, e pode ser dada pela função horária das velocidades, usando o tempo total do salto:
v é igual a v subscrito 0 menos 'g' vezes 't' implica em v é igual a 12 menos 10 vezes 2 vírgula 4 implica em v é igual a 12 menos 24 portanto v é igual a menos 12 metros por segundo
Página 77
Lançamento horizontal e oblíquo
Observe a imagem e, em seguida, responda à pergunta.
Imagens desta página sem proporção e em cores fantasia.

4. Por que o atleta de tiro com arco não deve atirar a flecha paralelamente ao solo se quiser acertar o centro do alvo?
Resposta: Porque ele deve considerar o movimento de queda da flecha em razão da ação da gravidade. Para acertar o centro do alvo, ele deve mirar acima do centro, considerando a queda da flecha, que fará um movimento com trajetória com formato de parábola.
Como visto anteriormente, a ação da gravidade pode alterar a velocidade dos corpos na direção vertical, fazendo-os cair. Essa ação também pode mudar o valor, a direção e o sentido da velocidade dos corpos, alterando sua trajetória.
Para compreender a situação do tiro com arco, imagine que uma esfera foi lançada rolando sobre uma mesa horizontal. Se as forças de atrito puderem ser desprezadas, a esfera realiza um movimento com velocidade constante. Mas, no instante em que essa esfera perde o contato com a superfície da mesa, ela começa a cair, e seu movimento passa a ser uma combinação de um movimento uniforme na horizontal com um movimento acelerado na vertical, resultando em uma trajetória que pode ser descrita como uma parábola.
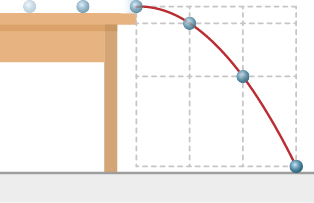
A análise do movimento pode ser feita com base nas seguintes relações.
Na horizontal
Como a velocidade na horizontal é constante, a posição do corpo nessa direção é dada por:
x é igual a v subscrito 0 vezes 't'
em que x é a posição do corpo na direção horizontal em metro, v subscrito 0 é a velocidade inicial do corpo em metro por segundo, e 't' é o tempo de queda em s.
Na vertical
Como o corpo está sendo acelerado pela gravidade na direção vertical, a posição dele é dada por:
y é igual a início de fração, numerador: 'g' vezes 't' elevado ao quadrado, denominador: 2, fim de fração
Sua velocidade é calculada por:
v subscrito y é igual a 'g' vezes 't' ou v subscrito y é igual a início de raiz quadrada; 2 vezes 'g' vezes y fim de raiz quadrada
Retomando a questão inicial, como a flecha e o centro do alvo estão à mesma altura do solo, se o atleta atirar a flecha paralelamente à direção horizontal, ela vai atingir o alvo em uma posição abaixo do centro. Lembrando que a ação da gravidade causa uma queda de 5 metros no primeiro segundo de movimento, o atleta deve considerar essa ação no momento do lançamento da flecha e mirar com certo ângulo para cima, em relação à horizontal.
Página 78
Agora, imagine que um golfista acaba de realizar uma tacada e a bolinha é lançada com uma velocidade que faz um ângulo abre parênteses teta fecha parênteses com a horizontal.
Imagens desta página sem proporção e em cores fantasia.

Dica
Acesse o simulador disponível em: https://s.livro.pro/01m825. Acesso em: 23 jul. 2024. Esse simulador explora o movimento de projéteis ao lançar diversos objetos, permitindo determinar como cada grandeza afeta sua trajetória, com ou sem resistência do ar.
A velocidade inicial abre parênteses expressão com detalhe acima, início da expressão, v, fim da expressão, início do detalhe acima, seta para a direita, fim do detalhe acima subscrito 0 fecha parênteses da bola de golfe pode ser dividida em suas componentes vertical e horizontal aplicando a trigonometria do triângulo retângulo:
v início subscrito, 0 subscrito x, fim subscrito é igual a v subscrito 0 vezes cosseno teta e v início subscrito, 0 subscrito y, fim subscrito é igual a v subscrito 0 vezes seno teta
Como o movimento horizontal é uniforme, a posição do corpo nessa direção é dada por:
x é igual a x subscrito 0 mais v subscrito x vezes 't' ou x é igual a x subscrito 0 mais abre parênteses v subscrito 0 vezes cosseno teta fecha parênteses vezes 't'
Na vertical, a análise do movimento é feita com base nas relações do movimento acelerado, de modo que a velocidade é obtida por:
v subscrito y é igual a v início subscrito, 0 subscrito y, fim subscrito menos 'g' vezes 't'
Já as posições verticais são dadas pela relação:
y é igual a y subscrito 0 mais v início subscrito, 0 subscrito y, fim subscrito vezes 't' menos início de fração, numerador: 'g' vezes 't' elevado ao quadrado, denominador: 2, fim de fração
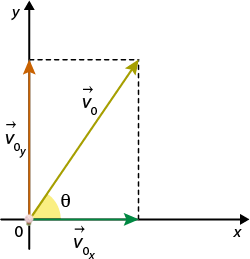
É importante perceber que, quando o projétil chega à altura máxima, sua velocidade na direção vertical é nula abre parênteses v subscrito y é igual a 0 fecha parênteses, contudo, a velocidade horizontal se mantém abre parênteses v subscrito x é igual a constante fecha parênteses. Além disso, caso a resistência do ar seja desprezada, o tempo de queda da altura máxima até a altura inicial de lançamento é igual ao intervalo de tempo de subida.
ATIVIDADES RESOLVIDAS
R3. Após uma tacada realizada por um golfista, uma bolinha de golfe adquiriu uma velocidade de 40 metros por segundo com direção de 30 graus em relação à horizontal. Nessas condições, qual distância a bolinha percorreu na horizontal? Considere: seno 30 graus é igual a 0 vírgula 5; cosseno 30 graus é aproximadamente igual a 0 vírgula 87.
Resolução
As velocidades na horizontal e na vertical são dadas por:
v subscrito x é igual a v subscrito 0 vezes cosseno 30 graus implica em v subscrito x é igual a 40 vezes 0 vírgula 87 portanto v subscrito x é igual a 34 vírgula 8 metros por segundo
v início subscrito, 0 subscrito y, fim subscrito é igual a v subscrito 0 vezes sen 30 graus implica em v início subscrito, 0 subscrito y, fim subscrito é igual a 40 vezes 0 vírgula 5 portanto v início subscrito, 0 subscrito y, fim subscrito é igual a 20 metros por segundo
Lembrando que, na altura máxima abre parênteses v subscrito y é igual a 0 fecha parênteses, o tempo de subida abre parênteses 't' subscrito 's' fecha parênteses da bolinha é:
v subscrito y é igual a v início subscrito, 0 subscrito y, fim subscrito menos 'g' vezes 't' implica em 0 é igual a 20 menos 10 vezes 't' subscrito 's' portanto 't' subscrito 's' é igual a 2 segundos
Como o tempo de queda é igual ao de subida, o tempo total de voo da bolinha é de 4 segundos; portanto, seu alcance é dado por:
x é igual a v subscrito x vezes 't' implica em x é igual a 34 vírgula 8 vezes 4 portanto x é igual a 139 vírgula 2 metros
Página 79
PRÁTICA CIENTÍFICA
Imagens desta página sem proporção e em cores fantasia.
Diferentes, mas iguais. Pode isso?
Por dentro do contexto
Diversos pensadores, como Aristóteles, Galileu Galilei e o inglês Isaac Newton (1643-1727), desenvolveram explicações para os movimentos de queda e de lançamento de projéteis. O entendimento dos fatores relacionados a esses movimentos permitiu o lançamento de foguetes e o posicionamento de satélites em órbita ao redor da Terra.
a ) Quais fatores podem influenciar o movimento de queda de um objeto?
Resposta: Os estudantes podem citar que, desprezando a resistência do ar, o movimento de queda depende somente da aceleração da gravidade. Já considerando a resistência do ar, a queda depende da massa e do formato do objeto.
Materiais
- régua de 30 centímetros
- duas moedas idênticas
- bancada ou superfície elevada
Como proceder
A. Junte-se a um colega e coloquem uma moeda sobre a borda de uma bancada, próximo a uma régua. A segunda moeda deve ser colocada sobre a extremidade da régua que está fora da superfície da bancada, como mostra a imagem.

B. Deem um leve toque na régua, de modo a permitir que a primeira moeda caia no chão, enquanto a segunda é lançada horizontalmente para fora da mesa.

C. Observem o movimento e ouçam com atenção o som da colisão das moedas com o solo.
D. Durante a execução da atividade, registrem por meio da gravação de um vídeo o movimento de queda das moedas.
E. Se julgarem necessário, repitam os procedimentos anteriores.
Análise e divulgação dos dados
1. O que aconteceu após a realização da etapa B? O que muda se você aplicar uma força maior para empurrar a régua?
Resposta: Espera-se que respondam que uma das moedas caiu em queda livre e a outra foi lançada horizontalmente, no entanto as duas chegaram ao solo ao mesmo tempo. Além disso, eles devem perceber que, aplicando uma força maior, a moeda lançada horizontalmente tem um alcance maior, porém ela atinge o solo no mesmo instante que a outra moeda.
2. Você acha que os resultados observados seriam os mesmos caso as moedas fossem diferentes uma da outra? Realize os procedimentos com pares de moedas diferentes entre si e verifique se sua hipótese se confirma.
Resposta: O objetivo dessa questão é levar os estudantes a levantar hipóteses sobre a queda de corpos com diferentes massas para investigar esse fenômeno. Espera-se que eles repitam os procedimentos listados na seção e verifiquem que as moedas diferentes também chegam ao solo ao mesmo tempo.
3. Com as imagens gravadas durante a realização dos procedimentos, produzam um vídeo para a divulgação dos resultados e das conclusões que vocês obtiveram após a prática. Apresentem o vídeo para os colegas de outras turmas e discutam também possíveis extensões ou variações do experimento para explorar ainda mais o tema da queda livre.
Resposta: O objetivo é levar os estudantes a divulgar os conhecimentos adquiridos durante a prática. Quanto aos vídeos, espera-se que eles comentem que a queda livre é um movimento que ocorre sob a ação da gravidade e que, nessa prática, a resistência do ar teve pouca influência porque a distância da queda é pequena.
Página 80
CONEXÕES com ... BIOLOGIA e QUÍMICA
Lixo espacial
Leia o trecho de reportagem a seguir.
Lixo espacial é problema crescente com soluções difíceis
Roberto Costa avalia os riscos que esses fragmentos representam para o funcionamento de satélites e as alternativas para reduzir a poluição na órbita da Terra
TAMMARO, Rodrigo. Lixo espacial é problema crescente com soluções difíceis. Jornal da USP no Ar, 11 maio 2022. Disponível em: https://s.livro.pro/sz48yx. Acesso em: 15 ago. 2024.
Você pode não os enxergar a olho nu enquanto observa o céu, mas ao redor da Terra há milhares de fragmentos de foguetes e naves espaciais, bem como satélites artificiais sem uso. Esses materiais são mantidos em órbita na Terra e compõem o chamado lixo espacial. Em razão da alta velocidade com que esses objetos se movem, até mesmo o impacto com aqueles de tamanho reduzido pode causar sérios danos a equipamentos em uso nessa região, além de graves acidentes, inclusive na superfície terrestre.
Afinal, o que levou ao acúmulo desses materiais ao redor da Terra? Há muito tempo o ser humano observa os astros a fim de compreender o Universo. O desenvolvimento da tecnologia possibilitou ao ser humano não apenas visualizar os astros com mais detalhes a partir da superfície terrestre, mas também observar o Universo e seus astros do espaço e chegar até alguns deles.
Em 1957, os soviéticos lançaram no espaço o primeiro satélite artificial não tripulado, chamado Sputnik 1. A partir de então, ao longo dos anos houve um acúmulo de materiais em torno da Terra, resultando em um cenário preocupante.
Imagens desta página sem proporção e em cores fantasia.
Desde o início da era espacial, em 1957, foram lançados no espaço aproximadamente 6 mil foguetes. Estes, por sua vez, foram responsáveis por lançar mais de 13 mil satélites artificiais na órbita da Terra.

Atualmente, há aproximadamente 9 mil satélites artificiais no espaço, dos quais um pouco mais de 6,7 mil estão em funcionamento. Além disso, entidades comerciais e governamentais estimam que mais de 478 mil satélites serão lançados até 2030.

Página 81
Imagens desta página sem proporção e em cores fantasia.
Estima-se que há na órbita da Terra aproximadamente:
- 36 mil objetos com tamanho superior a 10 centímetros;
- 1 milhão de objetos com tamanho entre 1 e 10 centímetros;
- 130 milhões de objetos com tamanho entre 1 milímetro e 1 centímetro.
Todos esses objetos espaciais equivalem a cerca de 10 mil toneladas de lixo orbitando o planeta.

Diversas empresas pelo mundo, públicas e privadas, estão desenvolvendo dispositivos capazes de capturar e eliminar os detritos presentes na órbita terrestre. Entre elas, destaca-se a empresa japonesa que construiu uma espaçonave equipada com uma placa magnética. Além disso, está desenvolvendo uma tecnologia para limpar o espaço por meio de braços mecânicos e trazê-los para a atmosfera da Terra, onde serão incendiados.

Imagens elaboradas com base em: SPACE debris by the numbers. The European Space Agency, 18 jun. 2024. Disponível em: https://s.livro.pro/3ig3m0. Acesso em: 23 jul. 2024.
A Estação Espacial Internacional é de extrema importância científica, desempenhando funções como de observatório, laboratório, local de construção e manutenção de equipamentos espaciais, entre outras. No entanto, ela está em perigo em razão do acúmulo de lixo espacial. Muitas vezes, seus tripulantes precisam executar manobras para evitar o choque com objetos que fazem parte desse lixo.
Assim, ao mesmo tempo que os avanços tecnológicos possibilitam ampliar ainda mais a exploração do Universo e interferem positivamente em diversos aspectos da vida em sociedade, o mau gerenciamento dessa tecnologia que se insere no espaço e muitas vezes não é removida pode ser prejudicial tanto para os estudos científicos como para a sociedade.
a ) De acordo com a Agência Espacial Europeia (ESA, sigla em inglês), semanalmente são emitidos alertas sobre o risco de colisão de dez de seus satélites artificiais com itens do lixo espacial. Reflita sobre as discussões apresentadas a seguir e produza um breve texto abordando por que o lixo espacial, embora distante da superfície terrestre, pode interferir em atividades do nosso dia a dia. Você considera importante a realização de monitoramento do lixo espacial? Quais são as possíveis consequências da colisão de itens do lixo espacial com satélites artificiais operantes para a população mundial?
Resposta pessoal. Espera-se que os estudantes reflitam sobre os impactos do lixo espacial em nosso dia a dia, especialmente quanto aos efeitos causados pela interrupção ou falha no funcionamento dos diferentes tipos de satélites artificiais, como os de comunicação, de navegação e os meteorológicos. Eles podem comentar que isso causa prejuízos na distribuição de sinais de telefonia, internet e televisão, mau funcionamento de dispositivos de rastreio e localização, como o GPS, e impacta de forma negativa no monitoramento do tempo e do clima, consequentemente afetando diversas atividades, como plantio e colheita.
b ) Faça uma pesquisa em sites voltada a outros projetos que visam à remoção do lixo espacial. Converse com os colegas a respeito desses projetos e reflitam sobre soluções, não apenas para remoção do lixo espacial existente, mas para evitar que mais lixo se acumule no espaço.
Resposta: Os estudantes poderão encontrar trabalhos como: o desenvolvimento de braço robótico, que utiliza um dispositivo com um adesivo, inspirado na pata de lagartixa, que tem capacidade de aderir a quase toda superfície, mesmo contra a gravidade; o uso de laser, que visa fragmentar o lixo espacial em tamanhos menores, facilitando sua remoção da órbita terrestre.
c ) O lixo espacial é um problema atual, assim como a produção excessiva de resíduos sólidos na superfície da Terra. Reflita sobre as possíveis maneiras de reduzir a geração de resíduos sólidos e, com quatro colegas, proponha possíveis soluções ao lixo espacial.
Resposta: O objetivo desta questão é levar os estudantes a refletir e, com base em um problema relacionado ao dia a dia deles, propor possíveis soluções para o lixo espacial. Para ambos os problemas (lixo espacial e resíduos sólidos), algumas medidas podem ser citadas, como: ampliar o tempo de uso dos objetos, evitando seu descarte; incentivar o descarte adequado de objetos e desenvolver materiais que possam se desintegrar com mais facilidade. Já no caso de ações contra o lixo espacial, alguns exemplos são: incentivar o desenvolvimento de tecnologias que ampliem o tempo de uso e de funcionamento dos equipamentos lançados ao espaço; desenvolver projetos de remoção desses itens do espaço, bem como de reaproveitamento deles, em vez de construir ou lançar outros itens, e promover pesquisas para desenvolver materiais que se desintegrem no ambiente espacial.
Página 82
ATIVIDADES
1. Um professor propõe um experimento mental no qual duas pequenas esferas de massas diferentes são lançadas verticalmente para cima da mesma altura e com velocidades iniciais iguais. Antes de realizar efetivamente o experimento, o professor pede aos estudantes que proponham algumas afirmativas sobre o experimento. As afirmativas são mencionadas a seguir.
I ) A esfera de menor massa atinge uma altura máxima maior.
II ) Ambas as esferas chegam ao solo com a mesma velocidade e ao mesmo tempo.
III ) Quando as esferas estão no ponto mais alto de suas respectivas trajetórias, a aceleração a que elas estão submetidas é nula.
Está(ão) correta(s) apenas a(s) afirmativa(s):
a ) I
b ) II
c ) III
d ) I e II
e ) II e III
Resposta: Alternativa b. Comentários nas Orientações para o professor.
2. O paraquedista austríaco Felix Baumgartner (1969 -), em 14 de outubro de 2012, saltou do limite superior da estratosfera, a cerca de 38.969 metros de altitude. Do instante do salto até a abertura do paraquedas, o movimento durou 4 minutos 20 segundos, e a velocidade máxima, de 1.357 vírgula 6 quilômetros por hora, foi alcançada nos primeiros 50 segundos de queda, ultrapassando a velocidade do som, que é de cerca de 1.224 quilômetros por hora.

Considerando que na estratosfera a gravidade é de aproximadamente 9 vírgula 7 metros por segundo quadrado, determine a velocidade do paraquedista após os primeiros 50 segundos de queda. O valor encontrado para a velocidade, baseando-se em seus cálculos, é igual ao valor atingido por Baumgartner? Converse com os colegas e justifique.
Resposta: v é igual a 1.746 quilômetros por hora. O valor é maior, pois se considera o corpo livre da ação de forças resistivas. Resolução nas Orientações para o professor.
3. Um atleta de salto ornamental abandona a plataforma de salto de 10 metros em queda livre. Estime o tempo que esse atleta tem para realizar suas acrobacias e sua velocidade ao entrar na água.
Resposta: 't' é aproximadamente igual a 1 vírgula 41 segundo e v é igual a 14 vírgula 1 metros por segundo. Resolução nas Orientações para o professor.
4. Considere três esferas A, B e C, lançadas simultaneamente para cima, com os valores de velocidade indicados na figura.
Imagem sem proporção e em cores fantasia.
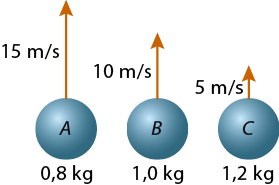
a ) Qual(is) esfera(s) ainda está(ão) subindo após 1 segundo do lançamento?
Resposta: Esfera A.
b ) Ordene as esferas em sequência crescente, de acordo com os módulos das acelerações, após 1 segundo do lançamento.
Resposta: a subscrito A é igual a a subscrito B é igual a a subscrito 'C' é igual a 'g'
5. Sobre o lançamento vertical para cima, desprezando a resistência do ar, verifique quais alternativas são verdadeiras.
Professor, professora: Comentários da questão 5 nas Orientações para o professor.
a ) A velocidade é nula na posição mais alta da trajetória.
Resposta: Verdadeira.
b ) A aceleração é nula na posição mais alta da trajetória.
Resposta: Falsa.
c ) O corpo executa um MRUV retardado na subida e um MRU na descida.
Resposta: Falsa.
d ) Se um objeto atingiu a altura máxima no instante 4 segundos, ele ocupa novamente a posição inicial no instante 8 segundos.
Resposta: Verdadeira.
e ) O corpo voltará a ter o módulo da velocidade inicial quando retornar à posição inicial.
Resposta: Verdadeira.
6. Segundo dados disponibilizados pelo pesquisador Paulo Felipe Jarschel, do Instituto de Física da Unicamp, se uma moeda de R$ 0,50 cair do topo do prédio mais alto do mundo, ela atinge a velocidade terminal de 94 vírgula 3 quilômetros por hora após 160 metros de queda, em razão da resistência do ar.
Sabendo que o prédio mais alto do mundo tem 828 metros de altura e considerando a aceleração gravitacional local igual a 10 metros por segundo quadrado, determine a razão entre a velocidade final da queda dessa moeda até o solo. Desconsidere a resistência do ar e a velocidade real adquirida por ela, entendendo que ambas partem do repouso.
a ) 1,4
b ) 2,1
c ) 3,4
d ) 4,9
e ) 6,1
Resposta: Alternativa d. Resolução nas Orientações para o professor.
Página 83
7. Um objeto é solto a partir do repouso de certa altura 'h' com relação ao solo. No mesmo instante, outro objeto é lançado horizontalmente da mesma altura. Considerando desprezível a resistência do ar, sobre essa situação, julgue os itens a seguir e dê a soma dos itens corretos.
Professor, professora: Comentários da questão 7 nas Orientações para o professor.
01 ) Os objetos chegam simultaneamente ao solo.
02 ) Em suas trajetórias, os dois objetos estão sujeitos à aceleração de mesmo módulo, direção e sentido.
04 ) O módulo da velocidade com que atingem o solo é o mesmo.
08 ) A distância entre os objetos antes de atingirem o solo é dada pelo produto v início subscrito, 0 subscrito x, fim subscrito vezes 't', em que v início subscrito, 0 subscrito x, fim subscrito é a velocidade inicial da partícula lançada horizontalmente e 't' é o instante de tempo.
16 ) O objeto lançado horizontalmente executa um movimento uniforme.
Resposta: Soma: 01 mais 0 2 mais 0 8 é igual a 11.
8. Hole in one é uma jogada de golfe na qual o golfista acerta a bola no buraco em apenas uma tacada. Suponha que um atleta está a uma distância horizontal de 200 metros do buraco, lançando a bola com uma velocidade inicial de 50 metros por segundo na direção 30 graus acima da horizontal. Desprezando a resistência do ar, verifique se é possível o atleta realizar um hole in one.
Considere 'g' é igual a 10 metros por segundo quadrado, seno 30 graus é igual a 0 vírgula 50 e cosseno 30 graus é igual a 0 vírgula 87.
Resposta: Não é possível. Resolução nas Orientações para o professor.
9. A imagem a seguir representa um corpo abandonado em queda livre abre parênteses v subscrito 0 é igual a 0 fecha parênteses no instante 't' subscrito 0 é igual a 0, em um local onde a aceleração da gravidade pode ser considerada 10 metros por segundo elevado ao quadrado.
Imagem sem proporção e em cores fantasia.

a ) Considerando que o referencial adotado vertical tem sentido para baixo, que a posição inicial é y subscrito 0 é igual a 0 e que a posição final corresponde aos braços da garota y é igual a 3 vírgula 2 metros, de forma que as posições aumentem durante a queda, determine a função horária das velocidades e a função horária das posições para esse movimento.
Resposta: v é igual a 10 vezes 't' e y é igual a 5 vezes 't' elevado ao quadrado. Resolução nas Orientações para o professor.
b ) Agora, complete um quadro como o mostrado a seguir, apresentando a velocidade e a posição do objeto em queda, para os tempos indicados na primeira coluna.
| t de s | v abre parênteses m barra s fecha parênteses | y de m |
|---|---|---|
|
0 |
||
|
0,4 |
||
|
0,8 |
Resposta: Para 't' é igual a 0, v é igual a 0 e y é igual a 0; t é igual a 0 vírgula 4 segundo, v é igual a 4 metros por segundo e y é igual a 0 vírgula 8 metro; 't' é igual a 0 vírgula 8 segundo, v é igual a 8 metros por segundo e y é igual a 3 vírgula 2 metros. Resolução nas Orientações para o professor.
RETOME O QUE ESTUDOU
Refletindo sobre o que estudou nesta unidade, responda às questões a seguir.
1. Qual foi a principal inovação do modelo heliocêntrico proposto pelo matemático polonês Nicolau Copérnico (1473-1543) e como ele desafiou a visão geocêntrica?
2. Como ocorre a formação de um sistema planetário a partir de uma estrela e qual é a fonte de energia das estrelas?
3. Qual é a diferença entre velocidade e aceleração? Como essas grandezas se relacionam com o movimento de um objeto?
4. Como as leis de Newton descrevem o comportamento dos objetos em movimento e em repouso e qual é a importância do uso do cinto de segurança em um veículo do ponto de vista da Física?
5. O que caracteriza o movimento de um objeto em queda livre e como a aceleração em razão da gravidade afeta esse movimento?
Respostas nas Orientações para o professor.
Página 84
MAIS QUESTÕES
1. (UEPG-PR) Sobre senso comum e método científico, assinale o que for correto.
01 ) O senso comum é caracterizado por uma forma de pensamento que não se respalda numa análise crítica e criteriosa dos fatos.
02 ) A ciência é uma forma de saber construído ao acaso, caracterizado pelo desinteresse na busca por justificativas e explicações objetivas e lógicas acerca dos fenômenos da natureza.
04 ) Os procedimentos descritos no método científico seguem uma estrutura lógica de pensamento e servem como orientação no processo de busca pela resolução de um problema.
08 ) O conhecimento científico se obtém pelo senso comum e pela prática de experimentos corriqueiros e aceitos conforme as questões culturais de uma sociedade.
Resposta: Soma: 01 mais 0 4 é igual a 0 5
2. (UERR) Na Física é muito importante que se saiba identificar quais grandezas são escalares e quais são vetoriais. Cada uma delas apresenta diferentes comportamentos quando se muda o referencial adotado para sua expressão. Nesse sentido, quando se muda o sistema de coordenada a partir do qual se escrevem grandezas escalares e vetoriais,
a ) as grandezas escalares não têm seu valor alterado e as grandezas vetoriais mantêm o mesmo valor para suas componentes.
b ) as grandezas escalares se alteram, assim como as componentes das grandezas vetoriais.
c ) as grandezas escalares se alteram, mas as componentes das grandezas vetoriais mantêm o mesmo valor para suas componentes.
d ) as grandezas escalares mantêm seu valor, mas as componentes das grandezas vetoriais se alteram.
e ) as componentes das grandezas escalares se alteram, mas o valor das grandezas vetoriais se mantém o mesmo.
Resposta: Alternativa d.
3. (Fuvest-SP) Em virtude do movimento das placas tectônicas, a distância entre a América do Sul e a África aumenta, nos dias atuais, cerca de 2 vírgula 0 centímetros a cada ano. Supondo que essa velocidade tivesse sido constante ao longo do tempo, e tomando uma distância atual de cerca de 5.000 quilômetros e entre os limites dessas duas massas continentais, indique a melhor estimativa para quanto tempo teria transcorrido desde quando ambas estavam unidas em um único supercontinente.
a ) 250.000 anos.
b ) 2.500.000 anos.
c ) 25.000.000 anos.
d ) 250.000.000 anos.
e ) 2.500.000.000 anos.
Note e adote:
O valor obtido, embora da ordem de magnitude correta, não é o mesmo calculado por estimativas mais precisas.
Resposta: Alternativa d.
Resolução nas Orientações para o professor.
4. (UEA) Um motorista faz uma viagem de carro por uma rodovia cuja velocidade máxima permitida é de 110 quilômetros por hora. Durante a viagem, o motorista repara que o velocímetro de seu carro está quebrado, o que impede que a velocidade do automóvel seja monitorada ao longo do percurso. Ao chegar a seu destino, o motorista percebe que levou 2,5 horas para fazer a viagem. Sabendo que o caminho percorrido foi de 300 quilômetros e que a rodovia possui monitoramento de velocidade por toda sua extensão, o motorista
a ) receberá uma multa, pois a velocidade média do carro foi de 120 quilômetros por hora.
b ) receberá uma multa, pois a velocidade média do carro foi de 130 quilômetros por hora.
c ) não receberá uma multa, pois a velocidade média do carro foi de 110 quilômetros por hora.
d ) receberá uma multa, pois a velocidade média do carro foi de 150 quilômetros por hora.
e ) não receberá uma multa, pois a velocidade média do carro foi de 90 quilômetros por hora.
Resposta: Alternativa a.
Resolução nas Orientações para o professor.
5. (UEPG-PR) A respeito da transitoriedade das teorias científicas, assinale o que for correto.
01 ) As teorias científicas podem ser refutadas, modificadas ou substituídas por outras.
02 ) As teorias científicas são definidas por verdades absolutas, portanto, são irrefutáveis e insubstituíveis, independentemente da época.
04 ) Os conhecimentos científicos de uma determinada época são sempre inquestionáveis e infalíveis, e isso constitui a evolução da produção científica.
08 ) A transitoriedade das teorias científicas demonstra a construção progressiva do conhecimento e a evolução da ciência.
Resposta: Soma: 01 mais 0 8 é igual a 0 9
Página 85
6. (UEM-PR) Cometas são corpos celestes que, junto com planetas e asteroides, fazem parte de sistemas estelares como o do Sol. Em relação a órbitas fechadas de cometas, considere a interação deles apenas com o Sol e a Teoria da Gravitação Universal de Newton. Assinale o que for correto.
01 ) Existe a possibilidade de órbitas de cometas serem circulares.
02 ) A 2ª Lei de Kepler (lei das áreas) pode ser aplicada a cometas do Sistema Solar.
04 ) A 3ª Lei de Kepler (lei dos períodos) se aplica a planetas, mas não a cometas.
08 ) O módulo da velocidade de um cometa em órbita elíptica é máximo no afélio.
16 ) O módulo da força gravitacional entre um cometa em órbita elíptica e o Sol é mínimo no periélio.
Resposta: Soma: 01 mais 0 2 é igual a 0 3
7. (UEPG-PR) O astrônomo alemão Johannes Kepler (1571-1630) analisou durante muitos anos as anotações de seu mestre TichoBrahe (1546-1601) sobre o movimento dos astros, e apresentou suas conclusões através de três leis, que passaram a ser designadas Leis de Kepler. Essas leis, juntamente com a Lei de Gravitação Universal de Newton, regem até hoje os estudos nessa área. Sobre o tema, assinale o que for correto.
01 ) A velocidade de um planeta em torno do Sol é variável. Ela aumenta à medida que o planeta se aproxima do Sol e diminui à medida que se afasta.
02 ) A aceleração da gravidade na superfície da Terra, ao nível do mar, vale aproximadamente 10 metros por segundo quadrado. Já na superfície da Lua, esse valor é aproximadamente igual a 1 vírgula 6 metro por segundo quadrado. Desse modo, podemos afirmar que, se a massa de um corpo vale 64 quilogramas na Terra, na Lua o valor dessa grandeza será 7 vezes menor.
04 ) A segunda lei de Kepler diz que "a linha que liga o Sol a um planeta que gira em órbita ao seu redor varre áreas iguais em intervalos de tempo iguais".
08 ) Dois satélites A e B, que giram ao redor de um planeta, têm períodos de translação iguais a T subscrito A é igual a 16 dias e T subscrito B é igual a 128 dias. Se o raio da órbita do satélite A vale R, o raio da órbita do satélite B corresponde a 4 vezes R.
Resposta: Soma: 01 mais 0 4 mais 0 8 é igual a 13
8. (Enem/MEC) Para um salto no Grand Canyon usando motos, dois paraquedistas vão utilizar uma moto cada, sendo que uma delas possui massa três vezes maior. Foram construídas duas pistas idênticas até a beira do precipício, de forma que no momento do salto as motos deixem a pista horizontalmente e ao mesmo tempo. No instante em que saltam, os paraquedistas abandonam suas motos e elas caem praticamente sem resistência do ar.
As motos atingem o solo simultaneamente porque
a ) possuem a mesma inércia.
b ) estão sujeitas à mesma força resultante.
c ) têm a mesma quantidade de movimento inicial.
d ) adquirem a mesma aceleração durante a queda.
e ) são lançadas com a mesma velocidade horizontal.
Resposta: Alternativa d.
9. (Enem/MEC) Em 20 de julho de 1969, Neil Armstrong tornou-se o primeiro homem a pisar na superfície da Lua. Ele foi seguido por Edwin Aldrin, ambos da missão Apollo 11. Eles, e os astronautas que os seguiram, experimentaram a ausência de atmosfera e estavam sujeitos às diferenças gravitacionais. A aceleração da gravidade na Lua tem 1 barra 6 do valor na Terra.
Em relação às condições na Terra, um salto oblíquo na superfície da Lua teria alcance
a ) menor, pois a força normal com o solo é menor.
b ) menor, pois a altura do salto seria maior.
c ) igual, pois o impulso aplicado pelo astronauta é o mesmo.
d ) maior, pois a aceleração da gravidade é seis vezes menor.
e ) maior, pois na ausência de atmosfera não há resistência do ar.
Resposta: Alternativa d.
10. (Enem/MEC) Sabe-se que a posição em que o Sol nasce ou se põe no horizonte muda de acordo com a estação do ano. Olhando-se em direção ao potente, por exemplo, para um observador no Hemisfério Sul, o Sol se põe mais à direita no inverno do que no verão.
O fenômeno descrito deve-se à combinação de dois fatores: a inclinação do eixo de rotação terrestre e a
a ) precessão do periélio terrestre.
b ) translação da Terra em torno do Sol.
c ) nutação do eixo de rotação da Terra.
d ) processão do eixo de rotação da Terra.
e ) rotação da Terra em torno de seu próprio eixo.
Resposta: Alternativa b.
Página 86
11. (Enem/MEC) No seu estudo sobre a queda dos corpos, Aristóteles afirmava que se abandonarmos corpos leves e pesados de uma mesma altura, o mais pesado chegaria mais rápido ao solo. Essa ideia está apoiada em algo que é difícil de refutar, a observação direta da realidade baseada no senso comum.
Após uma aula de física, dois colegas estavam discutindo sobre a queda dos corpos, e um tentava convencer o outro de que tinha razão:
Colega A: "O corpo mais pesado cai mais rápido que um menos pesado, quando largado de uma mesma altura. Eu provo, largando uma pedra e uma rolha. A pedra chega antes. Pronto! Tá provado!".
Colega B: "Eu não acho! Peguei uma folha de papel esticado e deixei cair. Quando amassei, ela caiu mais rápido. Como isso é possível? Se era a mesma folha de papel, deveria cair do mesmo jeito. Tem que ter outra explicação!".
(HÜLSENDEGER, M. Uma análise das concepções dos alunos sobre a queda dos corpos. Caderno Brasileiro de Ensino de Física, n. 3, dez. 2004 adaptado).
O aspecto físico comum que explica a diferença de comportamento dos corpos em queda nessa discussão é o(a)
a ) peso dos corpos.
b ) resistência do ar.
c ) massa dos corpos.
d ) densidade dos corpos.
e ) aceleração da gravidade.
Resposta: Alternativa b.
12. (Enem/MEC) Em um dia de calor intenso, dois colegas estão a brincar com a água da mangueira. Um deles quer saber até que altura o jato de água alcança, a partir da saída de água, quando a mangueira está posicionada totalmente na direção vertical. O outro colega propõe então o seguinte experimento: eles posicionarem a saída de água da mangueira na direção horizontal, a 1 metro de altura em relação ao chão, e então medirem a distância horizontal entre a mangueira e o local onde a água atinge o chão. A medida dessa distância foi de 3 metros, e a partir disso eles calcularam o alcance vertical do jato de água. Considere a aceleração da gravidade de 10 metros vezes s elevado a menos 2.
O resultado que eles obtiveram foi de
a ) 1 vírgula 50 metro.
b ) 2 vírgula 25 metros.
c ) 4 vírgula 0 0 metros.
d ) 4 vírgula 50 metros.
e ) 5 vírgula 0 0 metros.
Resposta: Alternativa b.
Resolução nas Orientações para o professor.
13. (Uerj) O menor tempo medido em laboratório ocorreu na escala de zeptossegundos e corresponde ao intervalo delta 't' em que uma partícula de luz percorre a distância que separa os centros atômicos de uma única molécula de hidrogênio. Uma unidade de zeptossegundo equivale a 10 elevado a menos 21 segundo. Admita que a velocidade da luz seja de 3 vezes 10 elevado a 8 metro por segundo e que a distância entre os centros atômicos de uma molécula de hidrogênio seja de 7 vírgula 2 vezes 10 elevado a menos 11 metro.
Nessas condições, no referencial da partícula de luz, o valor de delta 't', em zeptossegundos, é igual a:
a ) 120
b ) 180
c ) 240
d ) 320
Resposta: Alternativa c.
Resolução nas Orientações para o professor.
14. (UFRGS-RS) Na figura abaixo, estão representados dois corpos de massas M maiúsculo e m minúsculo, com M maiúsculo é maior do que 'm' minúsculo, unidos por um fio inextensível e de massa desprezível que passa por uma polia, também de massa desprezível e sem atrito.
Sendo g o módulo da aceleração da gravidade local, o módulo da aceleração de qualquer um dos dois corpos é dado por
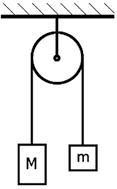
a ) abre parênteses M maiúsculo menos 'm' minúsculo fecha parênteses 'g' barra abre parênteses M maiúsculo mais 'm' minúsculo fecha parênteses.
b ) abre parênteses M maiúsculo menos 'm' minúsculo fecha parênteses 'g' barra 'm' minúsculo.
c ) M maiúsculo 'g' barra 'm' minúsculo.
d ) 'm' minúsculo 'g' barra abre parênteses M maiúsculo mais 'm' minúsculo fecha parênteses.
e ) M maiúsculo 'g' barra abre parênteses M maiúsculo mais 'm' minúsculo fecha parênteses.
Resposta: Alternativa a.
Resolução nas Orientações para o professor.
15. (Enem/MEC) Um Buraco Negro é um corpo celeste que possui uma grande quantidade de matéria concentrada em uma pequena região do espaço, de modo que sua força gravitacional é tão grande que qualquer partícula fica aprisionada em sua superfície, inclusive a luz. O raio dessa região caracteriza uma superfície-limite, chamada de horizonte de eventos, da qual nada consegue escapar. Considere que o Sol foi instantaneamente substituído por um Buraco Negro com a mesma massa solar, de modo que o seu horizonte de eventos seja de aproximadamente 3 vírgula 0 quilômetros.
(SCHWARZSCHILD, K. On the Gravitational Field of a Mass Point According to Einstein's Theory). Disponível em: https://s.livro.pro/sp4ewj. Acesso em: 26 maio 2022 (adaptado).
Após a substituição descrita, o que aconteceria aos planetas do Sistema Solar?
a ) Eles se moveriam em órbitas espirais, aproximando-se sucessivamente do Buraco Negro.
b ) Eles oscilariam aleatoriamente em torno de suas órbitas elípticas originais.
c ) Eles se moveriam em direção ao centro do Buraco Negro.
d ) Eles passariam a precessionar mais rapidamente.
e ) Eles manteriam suas órbitas inalteradas.
Resposta: Alternativa e.
Página 87
16. (Uece) O balão de ar quente foi o primeiro veículo aéreo de sucesso construído pelo homem. O primeiro voo tripulado em um balão de ar quente foi realizado em 1783. Os franceses Jean François e François Laurent realizaram esse feito num balão criado pelos irmãos Montgolfier. Em um balão, o compartimento que mantém o ar quente em seu interior é denominado envelope. Suspenso e fixado a este, encontra-se o cesto do balão. Um balão de massa total M (Envelope mais Cesto) desce verticalmente com uma aceleração A abre parênteses A é menor do que G fecha parênteses, onde G representa a aceleração da gravidade local. Para que o balão possa ascender com uma aceleração de mesmo módulo A, é necessário eliminar uma certa massa m do cesto do balão. Suponha que a força de sustentação que atua no balão em virtude da diferença de temperatura entre o interior e o exterior do Envelope não sofre mudanças em virtude da variação em sua massa. Ao desprezar todos os efeitos resistivos que porventura possam atuar no balão durante o processo, a massa m a ser eliminada é dada por
Resolução nas Orientações para o professor.
a ) 2 M A barra abre parênteses G mais A fecha parênteses.
b ) 2 M A G
c ) 2 M G barra A
d ) M G barra abre parênteses G mais A fecha parênteses
Resposta: Alternativa a.
17. (Unesp) A imagem mostra o exoplaneta 2M1207b em órbita ao redor de sua estrela 2M1207 na constelação de Centauro, distantes 40 unidades astronômicas um do outro. Esse é o primeiro exoplaneta do qual se obteve uma imagem direta. Em comparação com objetos do sistema solar, sabe-se que esse exoplaneta tem uma massa correspondente a 5 vezes a massa do planeta Júpiter e que sua estrela tem massa igual a 0,025 vezes a massa do Sol.
Imagem sem proporção e em cores fantasia.
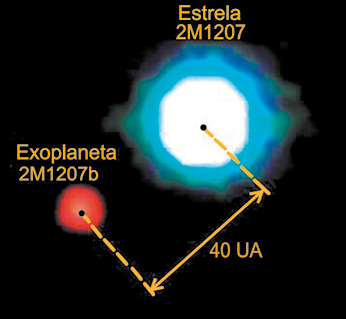
(https://s.livro.pro/cx7dfb. Adaptado.)
Considere os seguintes dados:
Massa do Sol: 2 vezes 10 elevado a 30 quilograma
Massa de Júpiter: 2 vezes 10 elevado a 27 quilograma
1 unidade astronômica: 1 vírgula 5 vezes 10 elevado a 11 metros
G é igual a constante universal de gravitação é igual a 6 vezes 10 elevado a menos 11 início de fração, numerador: N vezes m elevado ao quadrado, denominador: quilograma quadrado, fim de fração
A intensidade da força de atração gravitacional entre o exoplaneta 2M1207b e sua estrela é de, aproximadamente,
Resolução nas Orientações para o professor.
a ) 8 vírgula 3 vezes 10 elevado a 20 Newtons.
b ) 5 vírgula 0 vezes 10 elevado a 20 Newtons.
c ) 2 vírgula 5 vezes 10 elevado a 21 Newtons.
d ) 3 vírgula 6 vezes 10 elevado a 21 Newtons.
e ) 4 vírgula 4 vezes 10 elevado a 21 Newtons.
Resposta: Alternativa a.
18. (UEA-AM) Considere a representação do Sistema Solar, em que os planetas descrevem órbitas ao redor do Sol.
De acordo com a terceira lei de Kepler, início de fração, numerador: T elevado ao quadrado, denominador: R elevado ao cubo, fim de fração é igual a k, em que T e R são, respectivamente, o período e o raio médio da órbita e k é uma constante, um dos planetas do Sistema Solar que possui um ano com menos de 365 dias é
Resolução nas Orientações para o professor.
Imagem sem proporção e em cores fantasia.
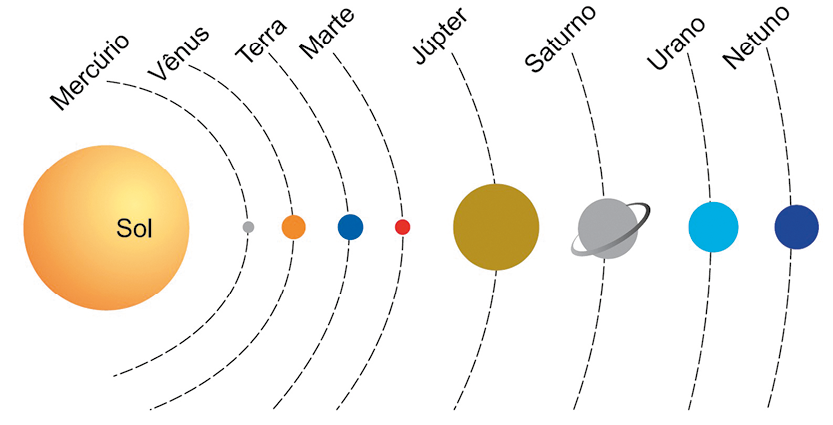
a ) Saturno.
b ) Urano.
c ) Marte.
d ) Vênus.
e ) Júpiter.
Resposta: Alternativa d.